Косой изгиб

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Лекция 6
Косой изгиб
Моменты инерции при повороте осей координат
Примеры определения геометрических характеристик
Авторы:
к.т.н., Войтко Александр Михайлович
1

2.

Пример: при монтаже оборудования силу F = 50 кН по небрежности отклонили на α = 5о. Определить, на
сколько изменится напряжение.
Решение:
Fz = 50∙sin 5o = 4,35 кН;
Fy = 50∙cos 5o = 49,8 кН;
М=2500кН/см
F=50кН
F=50кН
2

3.

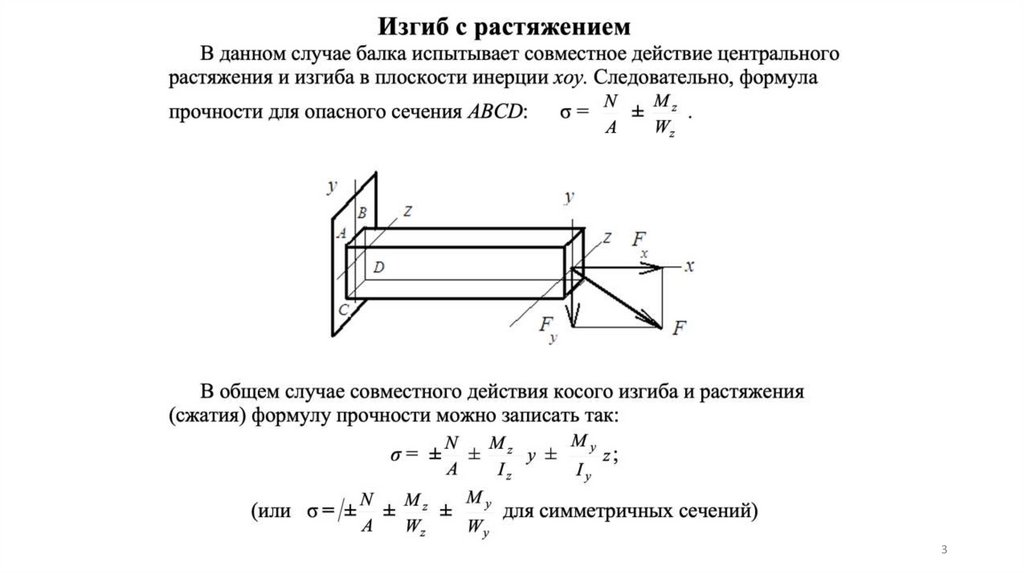
3

4.

Моменты инерции при повороте осей координат
1. Формулы преобразования координат.
y1 y cos z sin ;
z1 z cos y sin .
(6.1)
2. Осевые моменты инерции.
I y1 z dA z cos y sin dA
2
2
1
A
2
A
z cos2 2 yz cos sin y 2 sin 2 dA cos2 z 2 dA
A
A
(6.2)
2cos sin yzdA sin 2 y 2 dA
A
A
I y cos2 I yz 2sin cos I z sin 2 .
4

5.

С учетом
I y1 I y cos2 I z sin 2 I yz sin 2 .
(6.3)
I z1 y dA y cos z sin dA
2
2
1
A
2
A
y cos 2 2 yz cos sin z 2 sin 2 dA cos 2 y 2 dA
A
A
2cos sin yzdA sin 2 z 2 dA
A
(6.4)
A
I z cos2 I yz 2sin cos I y sin 2 .
I z1 I z cos2 I y sin 2 I yz sin 2 .
(6.5)
5

6.

1 cos 2
1 cos 2
2
cos
, sin
.
2
2
2
(6.6)
С учетом (6.6) формулы (6.3) и (6.5) получают вид
1 cos 2
1 cos 2
Iz
I yz sin 2
2
2
I y Iz I y Iz
cos 2 I yz sin 2 .
2
2
I y1 I y
1 cos 2
1 cos 2
I z1 I z
Iy
I yz sin 2
2
2
I y Iz Iz I y
cos 2 I yz sin 2 .
2
2
(6.7)
(6.8)
6

7.

Сложим левые и правые части формул (6.7) и (6.8):
I y1 I z1 I y I z .
(6.9)
Свойство осевых моментов инерции:
при повороте координатных осей сумма моментов инерции относительно
двух взаимно ортогональных осей не меняется.
3. Центробежный момент инерции.
I y1z1 y1 z1dA y cos z sin z cos y sin dA
A
A
z 2 sin cos y 2 sin cos yz cos 2 sin 2 dA
(6.10)
A
I y I z sin cos I yz cos 2 sin 2 .
7

8.

2sin cos sin 2 ; cos2 sin 2 cos 2 .
(6.11)
Формула (6.10) принимает вид с учетом (6.11):
I y1 z1
I y Iz
2
sin 2 I yz cos 2 .
(6.12)
При α = 90°:
I y1z1 I yz .
(6.13)
Свойство центробежных моментов инерции:
при повороте координатных осей на 90° центробежный момент
инерции сохраняет свою величину и меняет знак.
8

9.

Формулы для осевых и центробежных моментов инерции
при повороте осей координат:
I y1
I z1
I y Iz
2
I y Iz
I y1z1
2
I y Iz
2
I y Iz
2
Iz I y
2
cos 2 I yz sin 2 .
cos 2 I yz sin 2 .
(6.14)
sin 2 I yz cos 2 .
9

10.

Примеры определения геометрических характеристик
Пример 1. Определить главные центральные
моменты инерции, моменты сопротивления и
радиусы инерции сечения.
1. Определение положения центра тяжести.
A A1 A2 2 4 6 2 20 cм2.
Sz
yC
0;
A
Az
8 0 12 3
z
1,8 см.
A
20
A
S y1
i 1i
C
i
10

11.

2. Определение главных моментов инерции.
Координаты центров тяжести в центральной
системе осей x и y:
a1 a2 0 ; b1 1,8 см; b2 1, 2 см.
Главные центральные моменты инерции:
3
3
4
2
2
6
I z I zi ai2 Ai
0
0 36,87 см4.
12
12
i
3
3
2
4
6
2
I y I yi bi2 Ai
1,82 8
1,22 12 57,87 см4.
12
12
i
11

12.

3. Определение осевых моментов сопротивления сечения.
Максимальные расстояния от главных осей до контура сечения:
ymax 3 см; zmax 3,8 см.
Осевые моменты сопротивления:
Iy
57,87
Wy
15, 23 см3;
zmax
3,8
Iz
38,67
Wz
12,89 см3.
ymax
3
4. Вычисление радиусов инерции сечения.
iy
Iy
57,87
1,7 см;
A
20
iz
Iz
38,67
1,4 см.
A
20
12

13.

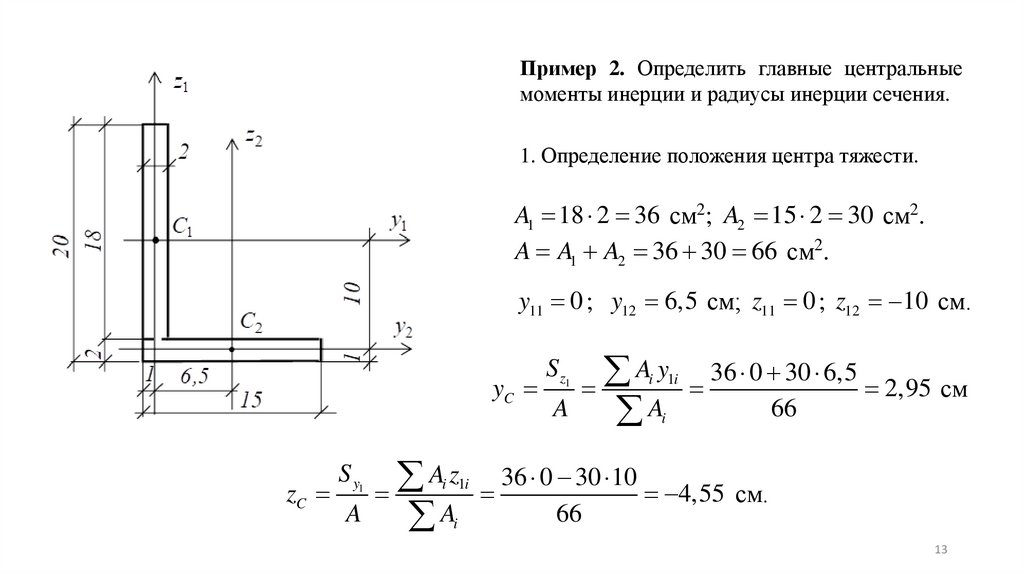
Пример 2. Определить главные центральные
моменты инерции и радиусы инерции сечения.
1. Определение положения центра тяжести.
A1 18 2 36 см2; A2 15 2 30 см2.
A A1 A2 36 30 66 см2.
y11 0 ; y12 6,5 см; z11 0 ; z12 10 см.
Ay
36 0 30 6,5
y
2,95 см
A
66
A
S z1
i 1i
C
i
Az
36 0 30 10
z
4,55 см.
A
66
A
S y1
i 1i
C
i
13

14.

Координаты центров тяжести в центральной
системе осей x0 и y0:
a1 y11 yC 0 2,95 2,95 см.
a2 y12 yC 6,5 2,95 3,55 см.
b1 z11 zC 0 4,55 4,55 см.
b2 z12 zC 10 4,55 5, 45 см.
2. Центральные осевые моменты инерции.
I y0 I yi bi2 Ai ; I z0 I zi ai2 Ai .
i
i
2 183
15 23
2
I y0
4,55 36
5,452 30 2618,4 см4.
12
12
3
18 23
2
15
I z0
2,952 36
3,552 30 1265,9 см4.
12
12
14

15.

3. Центробежный момент инерции.
I y0 z0 I yi zi ai bi Ai 2,95 4,55 36 3,55 5,45 30 1074,3
i
см4.
4. Положение главных осей инерции.
2 1074,3
tan 2 0
1,59 .
I y0 I z0
2618,4 1265,9
2 I y0 z0
2 57 30 ; 28 45 .
5. Главные центральные моменты инерции.
I y0 I z0
2
1
I гл
I y0 I z0 4 I y20 z0
2
2
2618,4 1265,9 1
2
2
2618,4 1265,9 4 1074,3 .
2
2
15

16.

I max 3211 см4; I min 673 см4.
Iy
I y0 I z0
I y0 I z0
cos 2 0 I yz sin 2 0
2
2
2618, 4 1265,9 2618, 4 1265,9
0,537 1074,3 0,843
2
2
= 3211 см4.
I y I max .
I z I min .
Проверка постоянства суммы моментов инерции.
I max I min I y0 I z0 . 3211 673 2618 1266 3884 см4.
16

17.

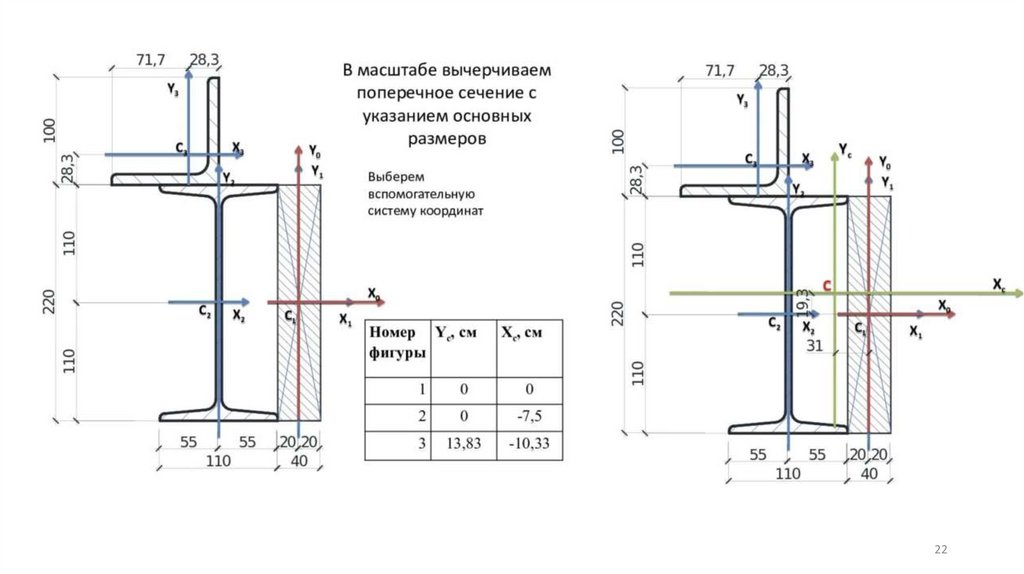
140*90*10
17

18.

18

19.

19

20.

20

21.

21

22.

22

23.

23

24.

24

25.

25

26.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра Строительной механики
Авторы:
к.т.н., Войтко Александр Михайлович
[email protected]
26