Similar presentations:
Вектор - направленный отрезок прямой
1.
2.
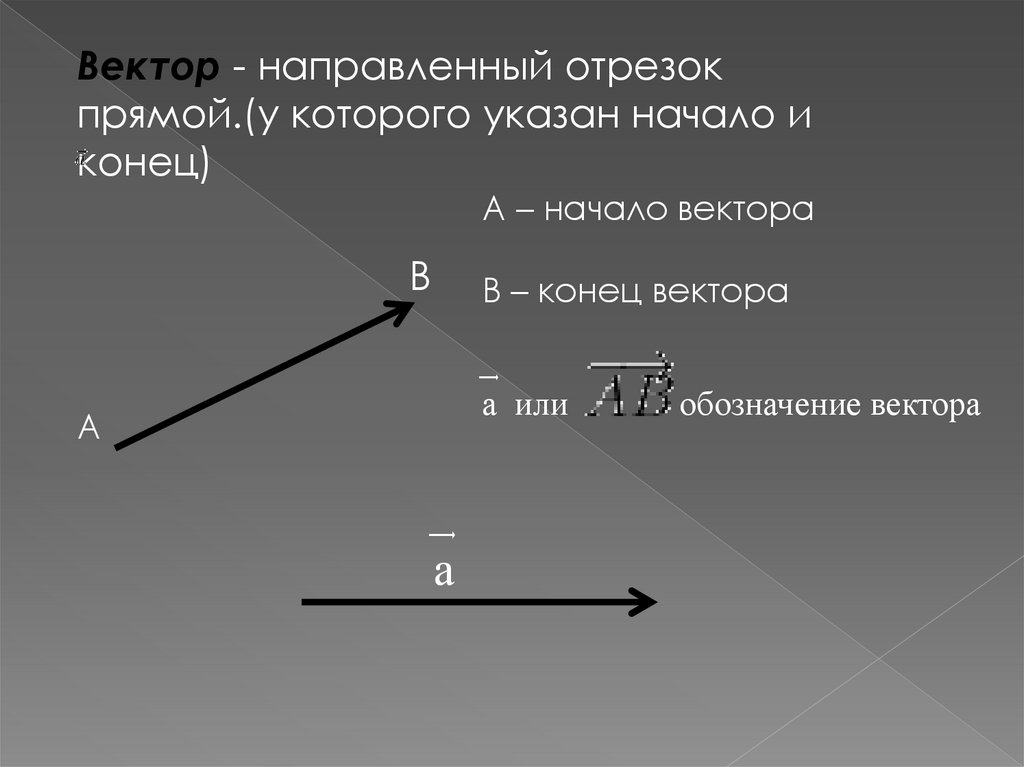
Вектор - направленный отрезокпрямой.(у которого указан начало и
конец)
А – начало вектора
В
В – конец вектора
͢
а или
А
͢
а
обозначение вектора
3.
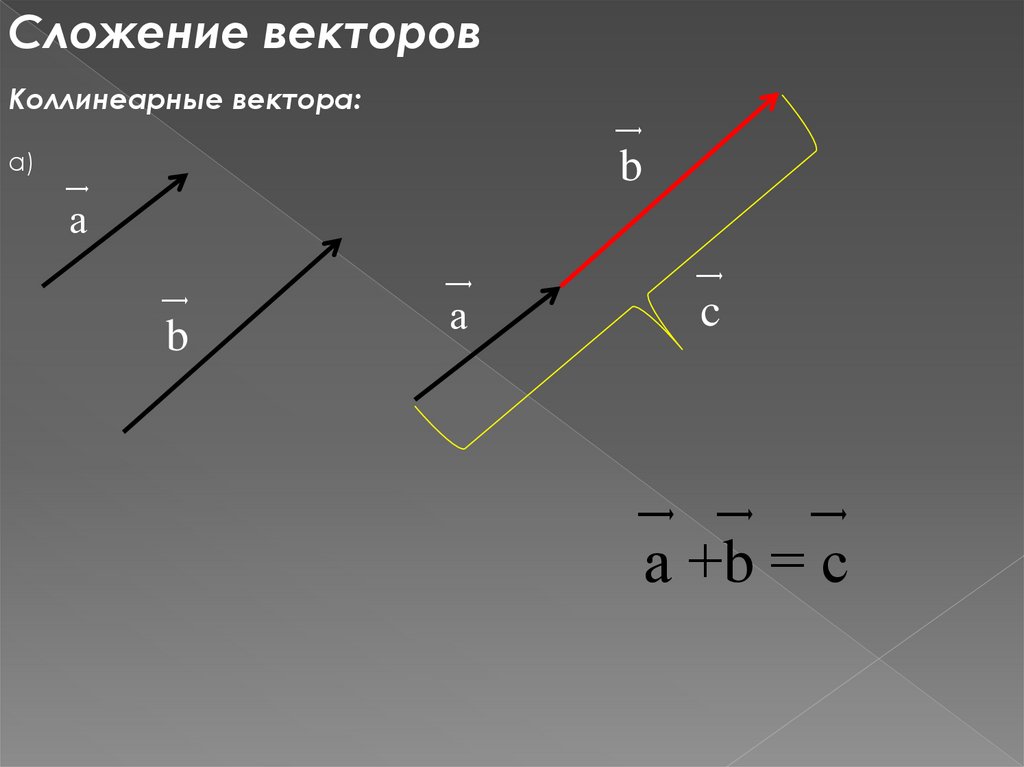
Сложение векторовКоллинеарные вектора:
͢
а)
b
͢
а
͢
b
͢
͢
а
c
͢
͢ ͢
а +b = с
4.
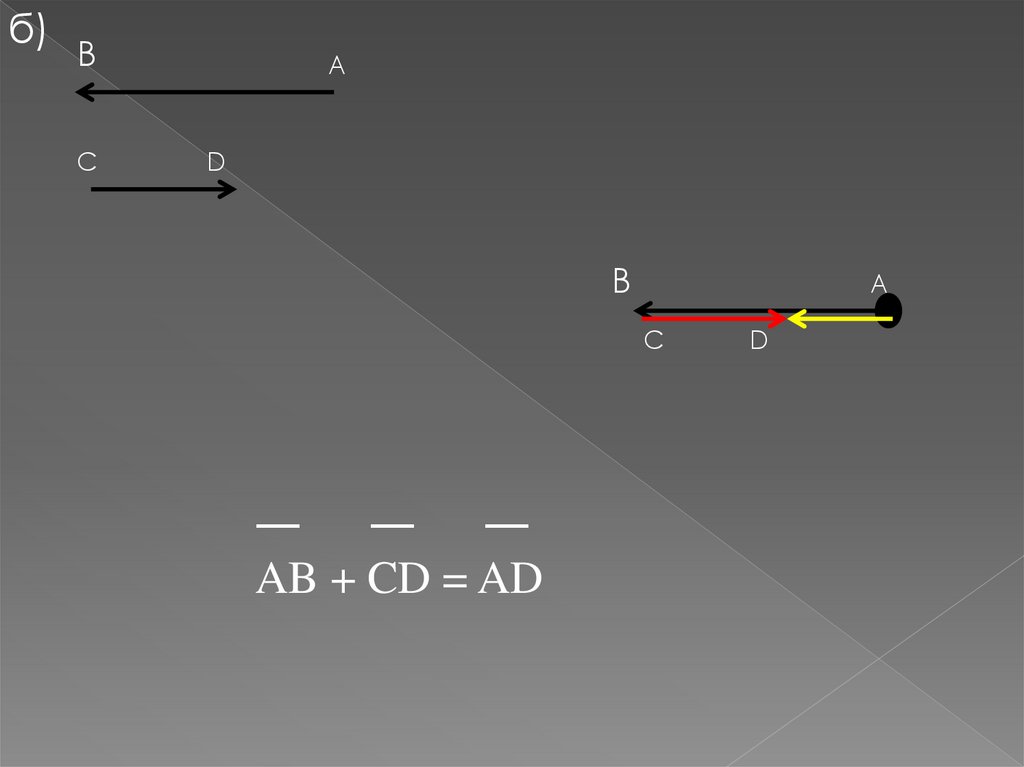
б)В
C
А
D
В
А
C
― ― ―
AB + CD = AD
D
5.
Неколлинеарные вектора:а)Правило треугольника
B
͢
͢
͢
а
b
а
͢
b
͢
A
Для любых трёх точек
верно равенство:
C
c
― ― ―
AB + BC = AC
6.
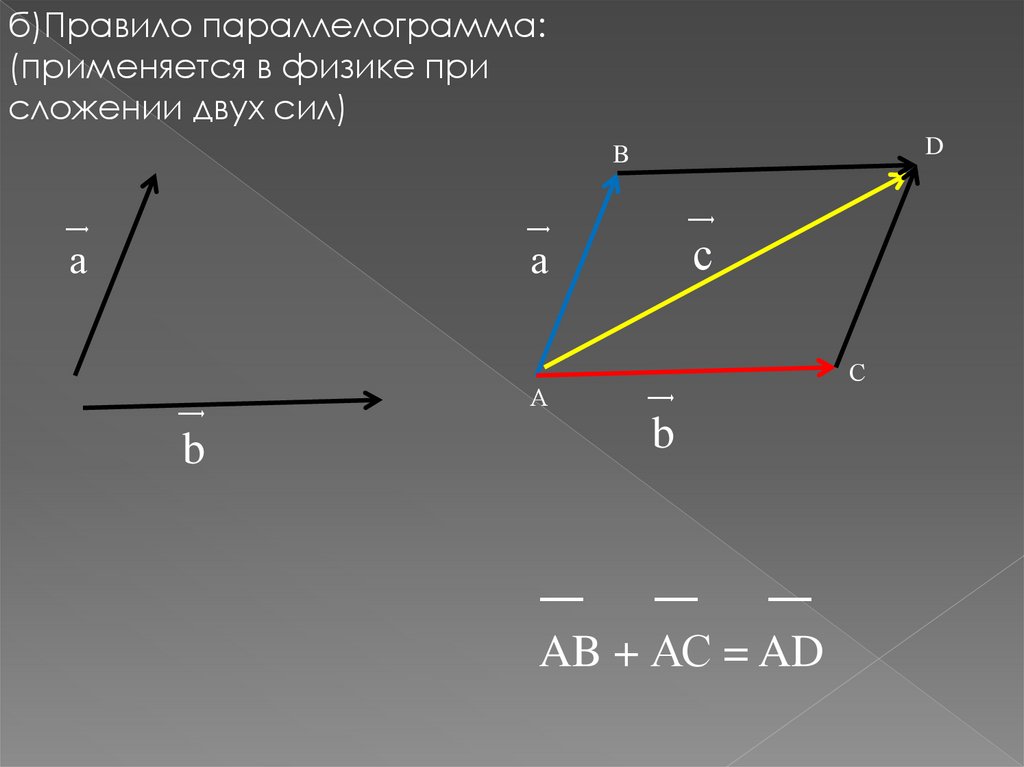
б)Правило параллелограмма:(применяется в физике при
сложении двух сил)
D
B
͢
͢
͢
а
а
͢
А
b
с
͢
С
b
― ― ―
AB + АС = AD
7.
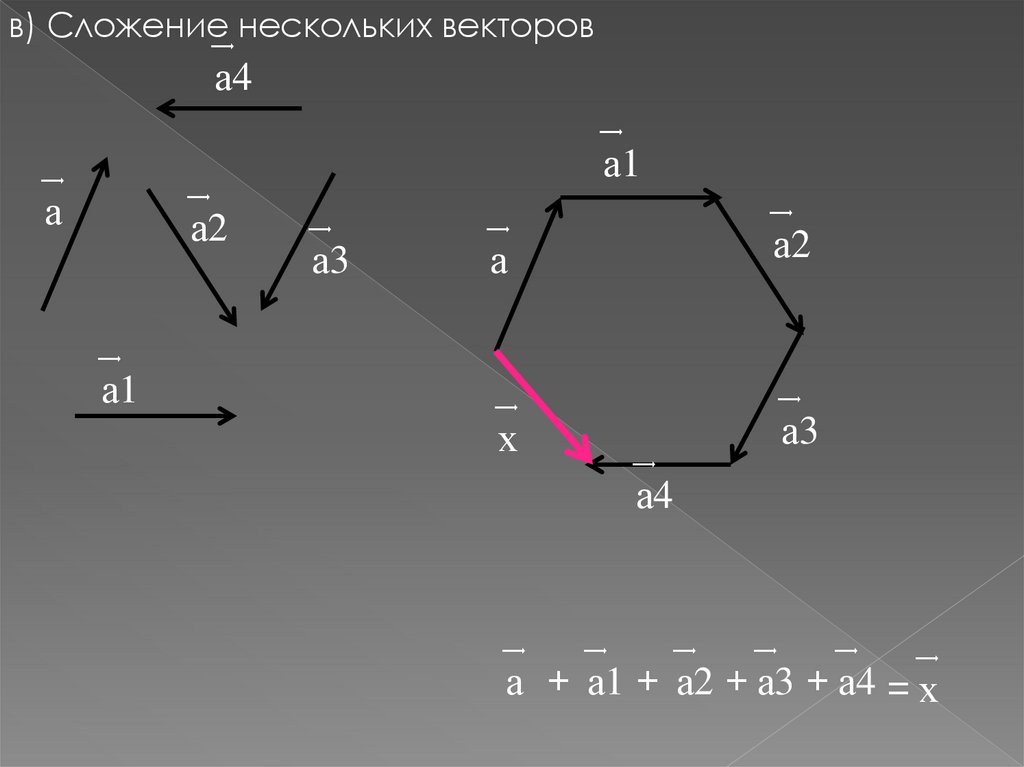
в) Сложение͢ нескольких векторова4
͢
а1
͢
а
͢
а2
͢
͢
͢
а3
а
а2
͢
͢
͢
а1
х
а3
͢
͢
а4
͢
͢
͢
͢
͢
а + а1 + а2 + а3 + а4 = х
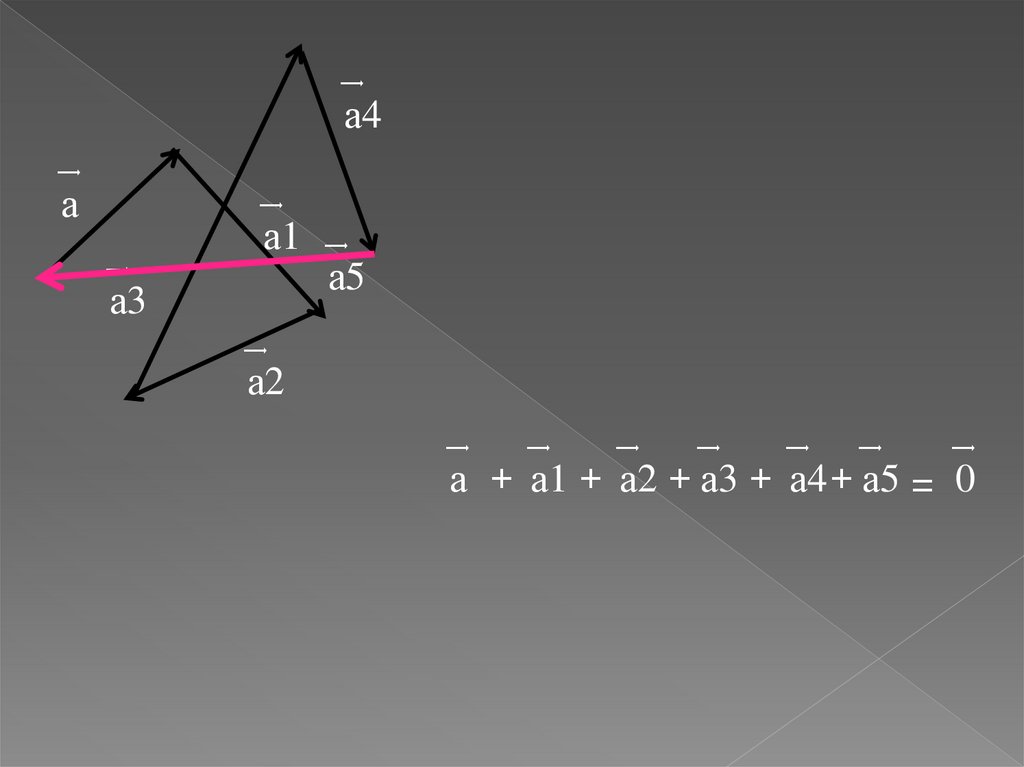
8.
͢а4
͢
͢
а
а1 ͢
͢
а3
а5
͢
а2
͢
͢
͢
͢
͢
͢
͢
а + а1 + а2 + а3 + а4 + а5 = 0
9.
Законы сложения векторов.Для любых векторов а,b, c справедливы
равенства:
͢
͢
͢
͢
1) а +b= b + a – переместительный закон
͢
͢
͢ ͢
͢ ͢
2) (а +b)+c=a+(b+c) – сочетательный закон
͢
͢
͢
3) а +0 = а – поглощение нулевого вектора
10.
Вычитание векторов.͢
Разностью двух векторов а и b
называется вектор с , сумма которого
с вектором b равняется вектору а.
͢
͢
͢ ͢
͢
а -b = с c+b = a
11.
I случай͢
а
A
͢
͢
͢
c
а
b
O
― ―
―
OA - OB = BA
͢
B
b
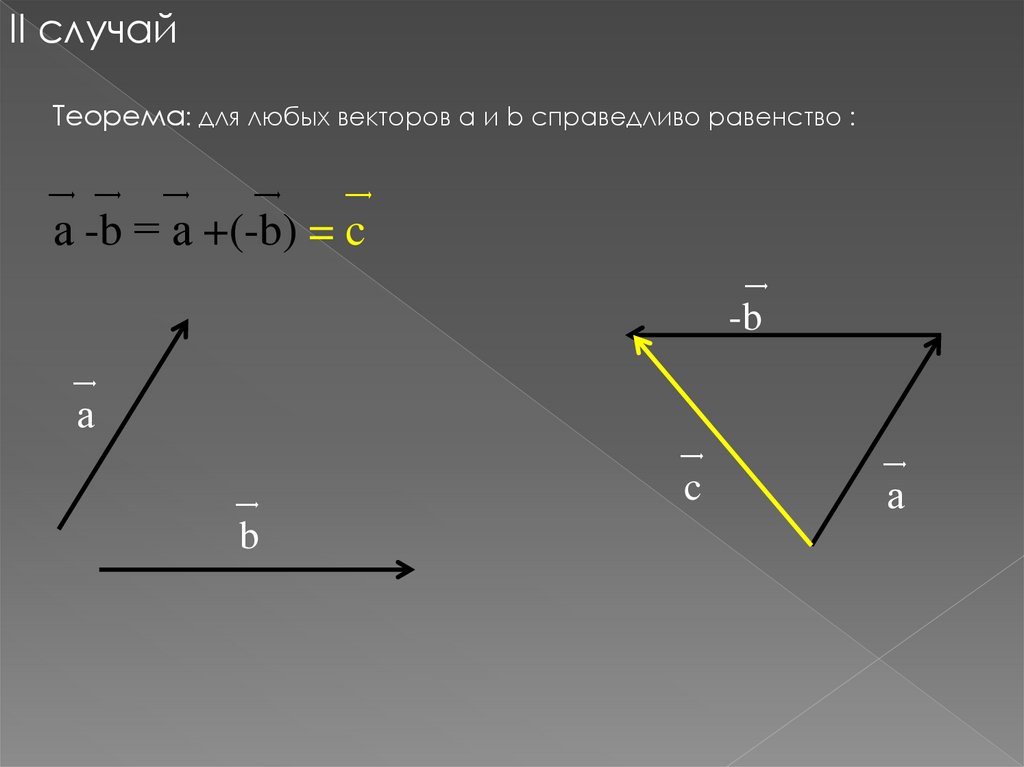
12.
II случайТеорема: для любых векторов а и b справедливо равенство :
͢
͢ ͢
͢
͢
а -b = а +(-b) = c
͢
-b
͢
а
͢
b
͢
͢
c
а
13.
͢Произведение не нулевого вектора͢ а на
любое число k равняется вектору b
→ →
b= a * k
→ →
1)│ b│= │a │* │k│
→ →
2)если k > 0 => b ↑↑ a
→ →
если k < 0 => b ↑↓ a
→ →
если k = 0 => b = 0
14.
Свойства умножения вектора на число.→
→
1)(m * n) * a = m * (a * n) – сочетательный
→
→ →
2)(m+n) * a = m*a + n*a – I
распределительный
→→
→
→
3)(a+b) * m=m*a + m*b – II
распределительный
→
→ →
4)0 * a = m*0 = 0 – поглощение нуля и
нулевого вектора
15.
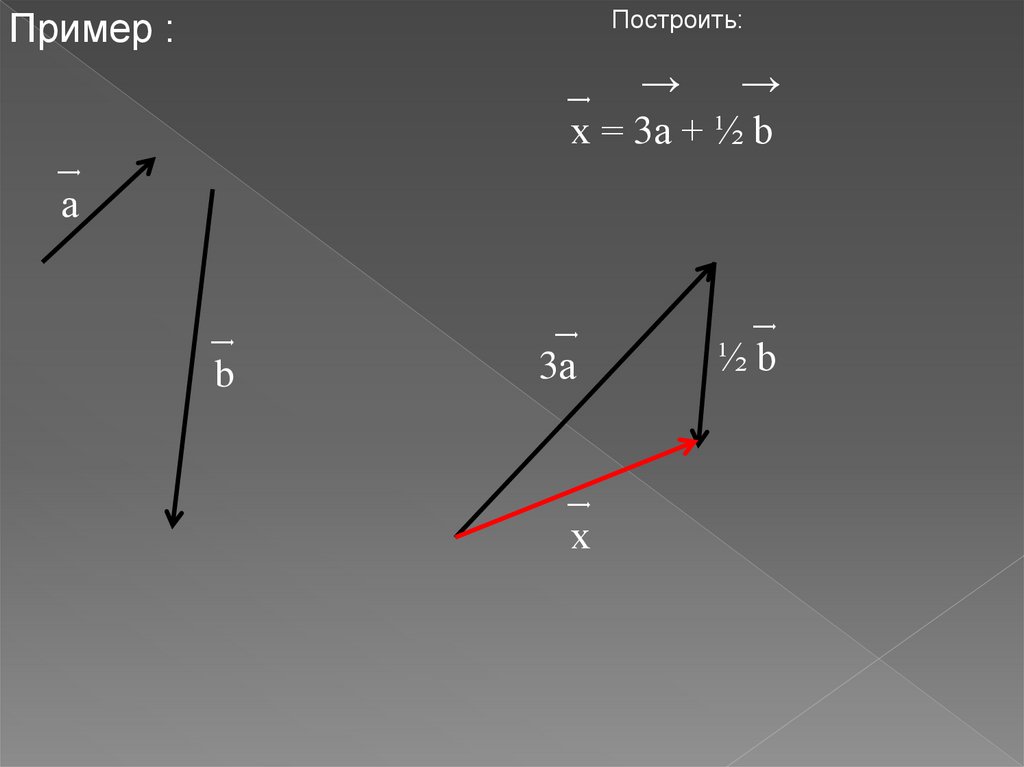
Построить:Пример :
͢
→
→
х = 3a + ½ b
͢
а
͢
b
͢
3а
͢
х
͢
½b







 mathematics
mathematics








