Задания с параметром (функциональный подход). Значение параметра

1. Задания с параметром.

(функциональный подход)

2.

Найдите все значения параметра а, при каждом из которых уравнение
x a 2 x x 2 2 x a 0 имеет более трех различных решений.
5
10
Решение.
Сгруппируем слагаемые в уравнении следующим образом
x x a 2 x а 2 x 0
10
5
2
Рассмотрим функцию
f (t ) t 5 t
Данная функция нечетная и монотонная, т.к.
f (t ) 5t 4 1,
f (x ) x
2
2 5
f (t ) 0, при t R
x x x
2
10
2
f (a 2 x ) a 2 x a 2 x
5
Таким образом, получим уравнение
f ( x 2 ) f (a 2 x ) 0

3.

f ( x 2 ) f (a 2 x )
Т.к. функция нечетная, то
f ( x ) f (2 x a)
2
Т.к. функция монотонная ,то получим уравнение
x 2x a
2
Выразим параметр, а, и применим графический метод
Таким образом уравнение имеет
три решения если
Ответ:
a 0; 1
a 0; 1
a x 2 x
2

4.

Найдите все значения параметра а, при которых система
имеет ровно 2 решения.
log a y ( x 2 2 x) 2
2
x y 2 x
Решение.
Рассмотрим второе уравнение системы :
x 2 y 2 x, y x 2 2 x,
С учетом того, что
y 0
Таким образом, если
y ( x 1) 2 1,
y 1
(из первого уравнения), получим, что
0 y 1
0 y 1
,то второе уравнение имеет два решения.
Значит, чтобы исходная система имела ровно два решения, необходимо,
что бы уравнение
log a y ( y ) 2
имеет ровно одно решение.
при
0 y 1

5.

Рассмотрим функции
Если
0 a 1
u log a y, u y 2
то,
Если
при
а 1
0 y 1
то,
Т.образом, уравнение имеет
Т.образом, уравнение не имеет решения
единственное решение, а исходная
система два.
Ответ:
0 a 1

6.

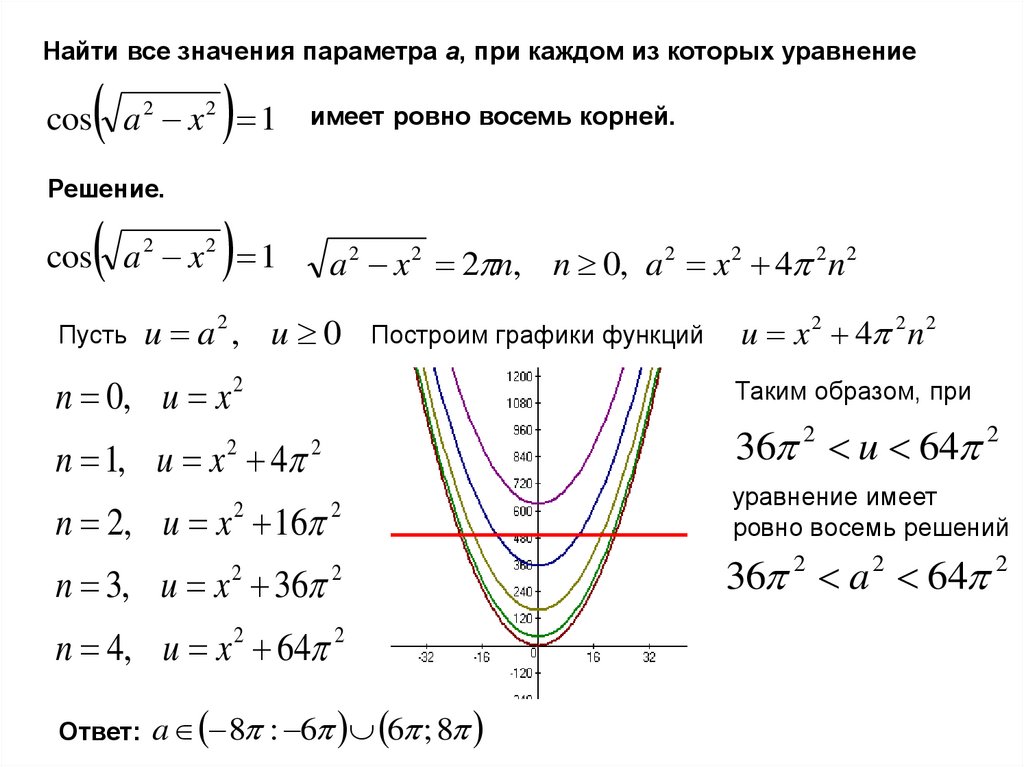
Найти все значения параметра а, при каждом из которых уравнение
cos a 2 x 2 1
Решение.
имеет ровно восемь корней.
cos a 2 x 2 1
Пусть
a 2 x 2 2 n, n 0, a 2 x 2 4 2 n 2
u a2 , u 0
Построим графики функций
n 0, u x 2
n 1, u x 4
2
u x 2 4 2 n 2
Таким образом, при
36 2 u 64 2
2
n 2, u x 16
2
уравнение имеет
ровно восемь решений
n 3, u x 36
2
36 2 a 2 64 2
2
2
n 4, u x 2 64 2
Ответ:
a 8 : 6 6 ; 8

7.

Найдите все значения параметра а, при которых при любых значениях
параметра b, уравнение
x 2 b 2 x 1 a имеет хотя бы одно решение.
Решение.
Преобразуем уравнение:
Рассмотрим функции
x 2 a b 2x 1
y x 2 a,
y b 2x 1
2; a
y x 2 a
вершина графика функции находится в точке
y b 2x 1
1
;
0
вершина графика функции находится в точке
2
Таким образом, уравнение имеет
хотя бы одно решение не зависимо
от значения параметра b, если оба
1
графика проходят через вершину ; 0
2
1
1
2 a b 2 1
2
2
a 2,5
Ответ: a 2,5