Similar presentations:
Графический подход к решению задач с параметром и модулем
1. Факультативное занятие в 11 классе: Графический подход к решению задач с параметром и модулем
МБОУ «Инсарская средняя общеобразовательная школа №1»Факультативное занятие в 11 классе:
Графический подход к решению
задач с параметром и модулем
подборка заданий для подготовки к ЕГЭ
Чудаева Елена Владимировна, учитель математики,
г. Инсар, Республика Мордовия
2.
Найдите все значения параметра а, прикоторых уравнение 2 х а х 3 1 имеет
единственное решение.
у
4
А
В
2
-4
-2
0
х
РЕШЕНИЕ.
Правая часть этого уравнения задает неподвижный
«уголок», левая – «уголок», вершина которого
двигается по оси абсцисс.
3.
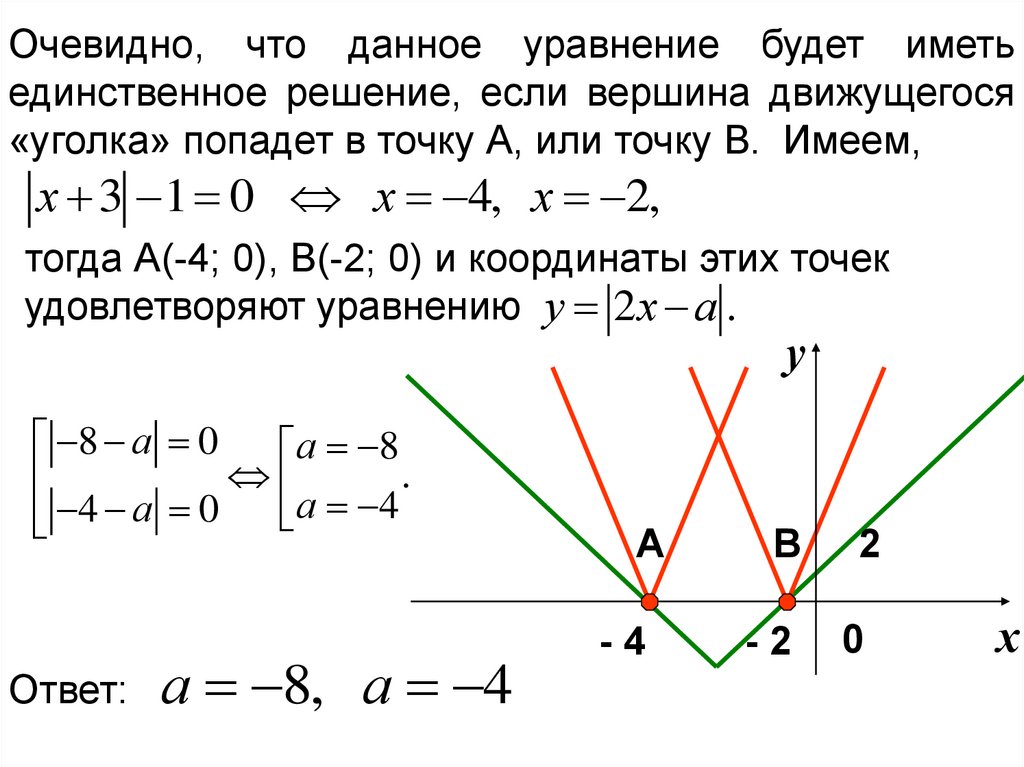
Очевидно, что данное уравнение будет иметьединственное решение, если вершина движущегося
«уголка» попадет в точку А, или точку В. Имеем,
х 3 1 0 х 4, х 2,
тогда А(-4; 0), В(-2; 0) и координаты этих точек
удовлетворяют уравнению у 2 х а .
у
8 а 0
а 8
.
а 4
4 а 0
Ответ:
а 8, а 4
А
-4
В
-2
2
0
х
4.
Графический способ решениязадач с параметром
Задачу с параметром можно рассматривать как функцию
f (x; a) =0
1. Строим графический образ
2. Пересекаем полученный график прямыми
параллельными оси абсцисс
Схема
решения:
3. «Считываем» нужную информацию
5.
Найти количество корней(а 2х х 2 )(а 1 х 1 ) 0
уравнения в зависимости от
параметра а
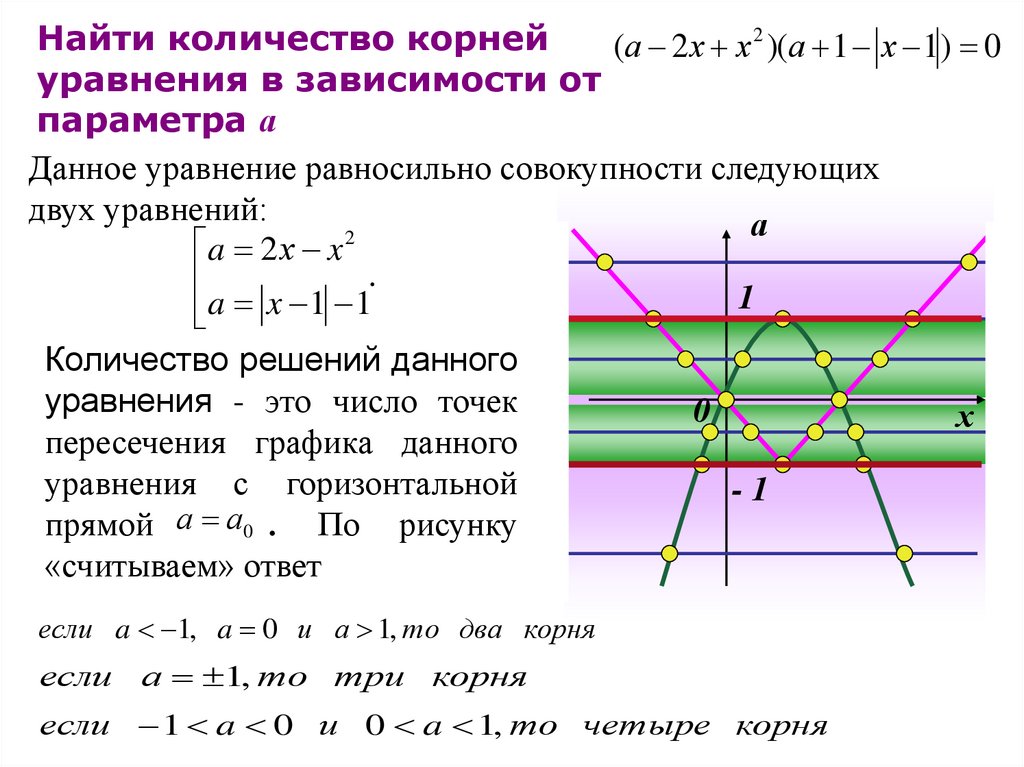
Данное уравнение равносильно совокупности следующих
двух уравнений:
а
2
a 2 х x
.
1
a x 1 1
Количество решений данного
уравнения - это число точек
0
х
пересечения графика данного
уравнения с горизонтальной
-1
прямой а а0 . По рисунку
«считываем» ответ
если a 1, a 0 и а 1, то два корня
если а 1, то три корня
если 1 a 0 и 0 a 1, то четыре корня
6.
ОБОБЩЕННЫЙ МЕТОД ОБЛАСТЕЙ(«переход» метода интервалов с прямой на плоскость)
Неравенства с
одной переменной
Метод интервалов:
1.ОДЗ
2. Корни
3. Ось
4. Знаки на
интервалах
5. Ответ.
Неравенства с
двумя переменной
Метод областей:
1. ОДЗ
2. Граничные линии
3. Координатная
плоскость
4. Знаки в областях
5.Ответ по рисунку.
7.
На координатной плоскостих2 у 2
изобразите множество точек, 2
0
2
удовлетворяющих неравенству х у 1
Найдем ОДЗ : х 2 у 2 1 0 х 2 у 2 1
2
2
2
2
х
у
0
у
х
и
х
у
1
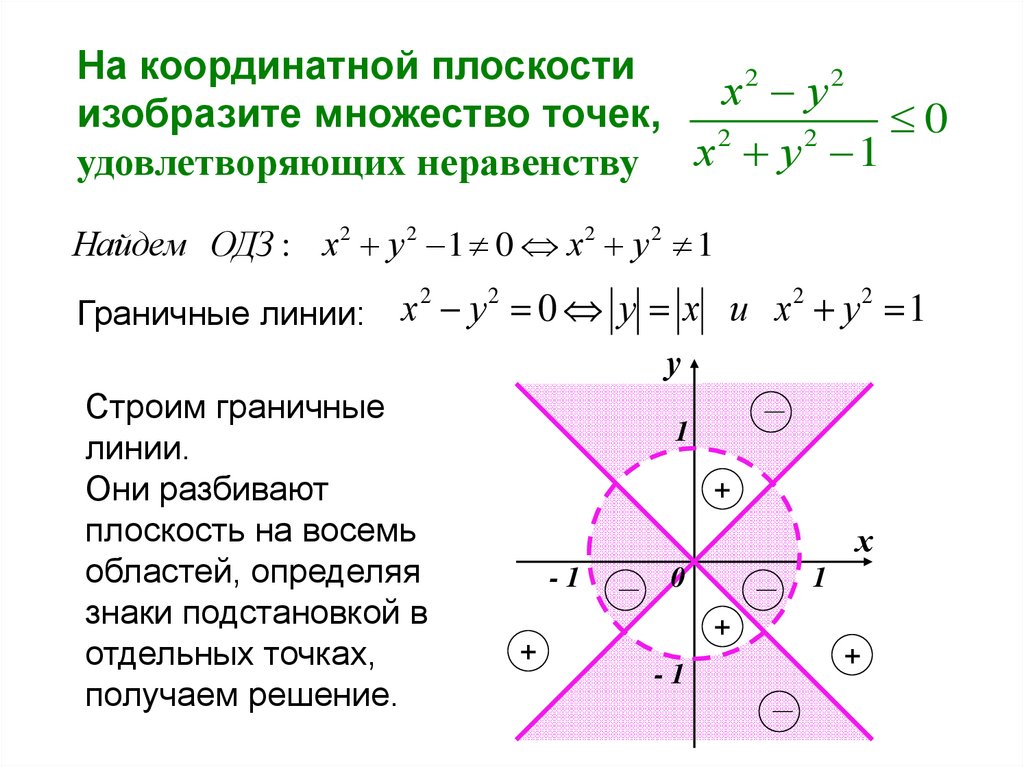
Граничные линии:
у
Строим граничные
линии.
Они разбивают
плоскость на восемь
областей, определяя
знаки подстановкой в
отдельных точках,
получаем решение.
1
+
х
-1
+
0
1
+
-1
+
8.
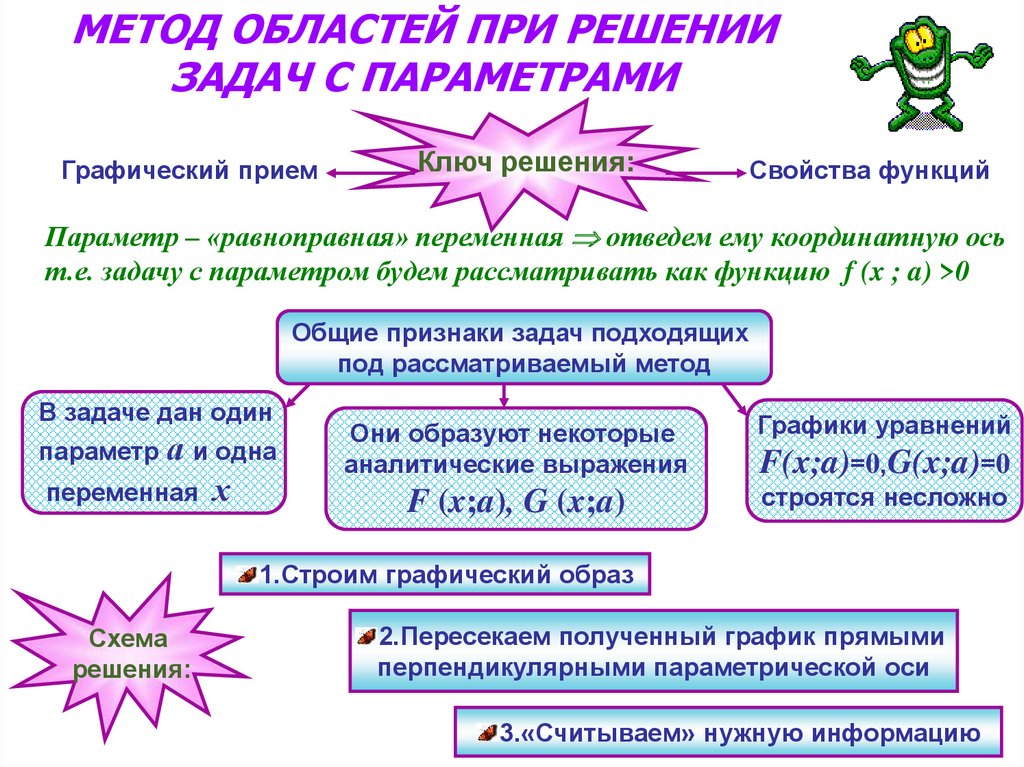
МЕТОД ОБЛАСТЕЙ ПРИ РЕШЕНИИЗАДАЧ С ПАРАМЕТРАМИ
Графический прием
Ключ решения:
Свойства функций
Параметр – «равноправная» переменная отведем ему координатную ось
т.е. задачу с параметром будем рассматривать как функцию f (x ; a) >0
Общие признаки задач подходящих
под рассматриваемый метод
В задаче дан один
а и одна
переменная х
параметр
Они образуют некоторые
аналитические выражения
Графики уравнений
F (x;a), G (x;a)
строятся несложно
F(x;a)=0,G(x;a)=0
1.Строим графический образ
Схема
решения:
2.Пересекаем полученный график прямыми
перпендикулярными параметрической оси
3.«Считываем» нужную информацию
9.
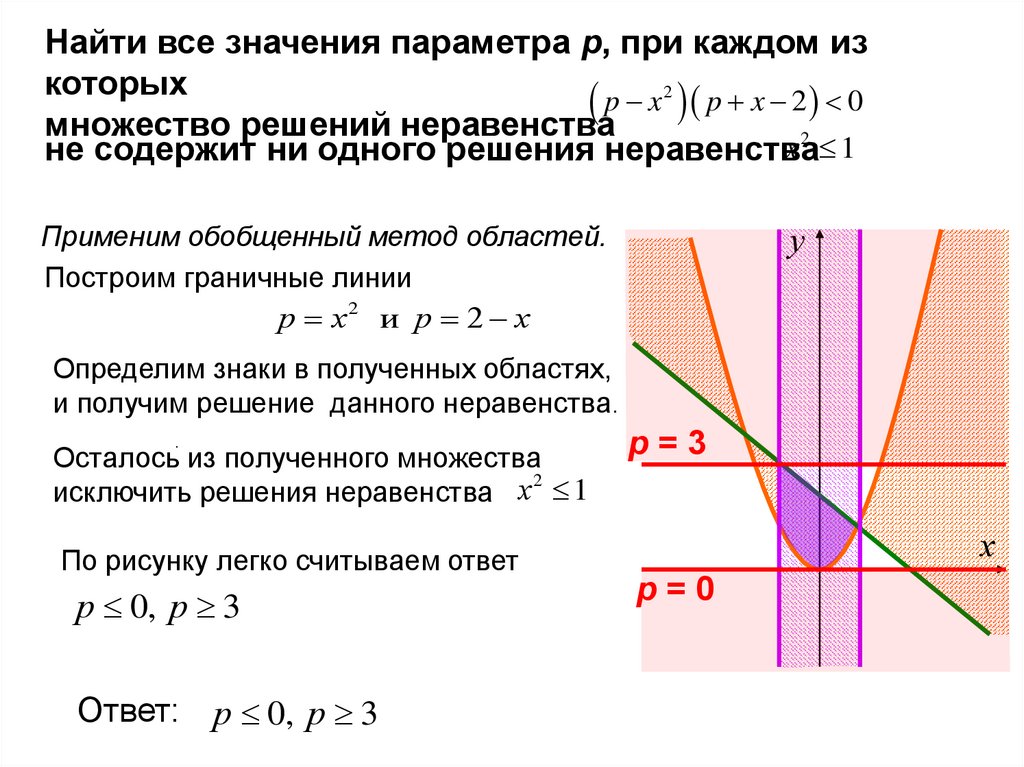
Найти все значения параметра р, при каждом изкоторых
p x2 p x 2 0
множество решений неравенства
х2 1
не содержит ни одного решения неравенства
Применим обобщенный метод областей.
Построим граничные линии
у
р х2 и р 2 х
Определим знаки в полученных областях,
и получим решение данного неравенства.
.
Осталось из полученного множества
2
исключить решения неравенства х 1
По рисунку легко считываем ответ
р 0, р 3
Ответ: р 0, р 3
р=3
х
р=0
10.
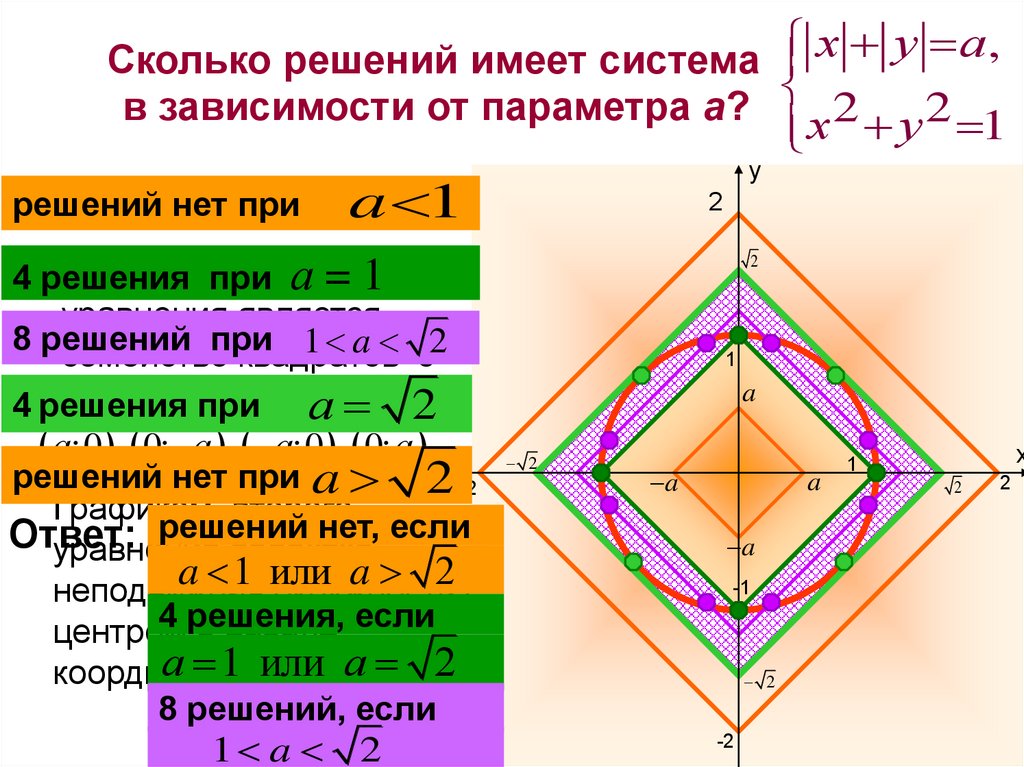
х у а,Сколько решений имеет система
в зависимости от параметра а?
2 у 2 1
х
решений нет при
y
a 1
Графикомпри
первого
4 решения
а=1
уравнения является
8 решений
при
1 a с2
семейство
квадратов
вершинами
4 решения
прив точках
а 2
а;0 , 0; а , а;0 , 0; а
решений нет при a 2 -2
Графиком второго
решений нет, если
Ответ:
уравнения является
a 1 или a 2
неподвижная окружность с
4 решения,
центром
в начале если
а 1и радиусом
или а 12
координат
8 решений, если
1 a 2
2
2
1
a
2
a
a
a
-1
2
-2
x
1
2
2
11.
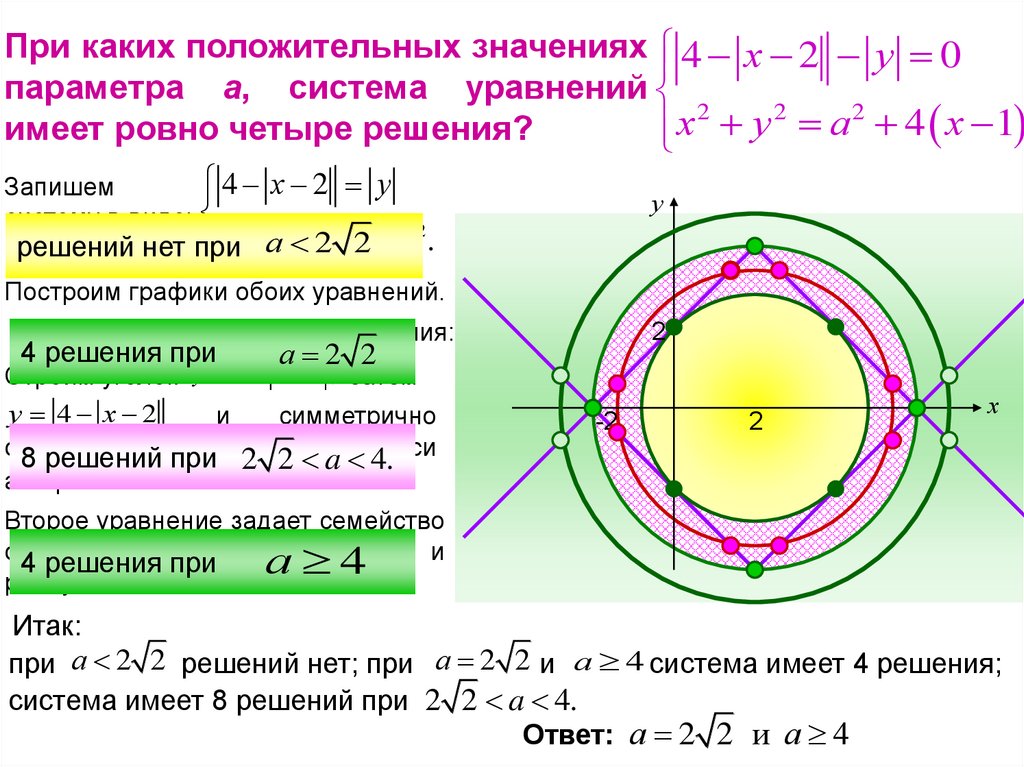
При каких положительных значениях 4 х 2 у 0параметра а, система уравнений
2
2
2
х
у
а
4 х 1
имеет ровно четыре решения?
4
Запишем
систему в виде:
х 2 у
у
2
2
2
(
х
2)
у
а
.
а
2
2
решений нет при
Построим графики обоих уравнений.
Шаги построения первого уравнения:
4 решения при
2
а 2 2
Строим уголок у 4 х 2 , затем
у 4 х 2
и
симметрично
отображаем
относительно
8 решений при
2 2 a 4. оси
абсцисс.
-2
2
х
Второе уравнение задает семейство
окружностей
с центром (2;0) и
4 решения при
а 4
радиусом а.
Итак:
при а 2 2 решений нет; при а 2 2 и а 4 система имеет 4 решения;
система имеет 8 решений при 2 2 a 4.
Ответ: а 2 2 и а 4
12.
Задачи,взятые из материалов ЕГЭ
прошлых лет
13.
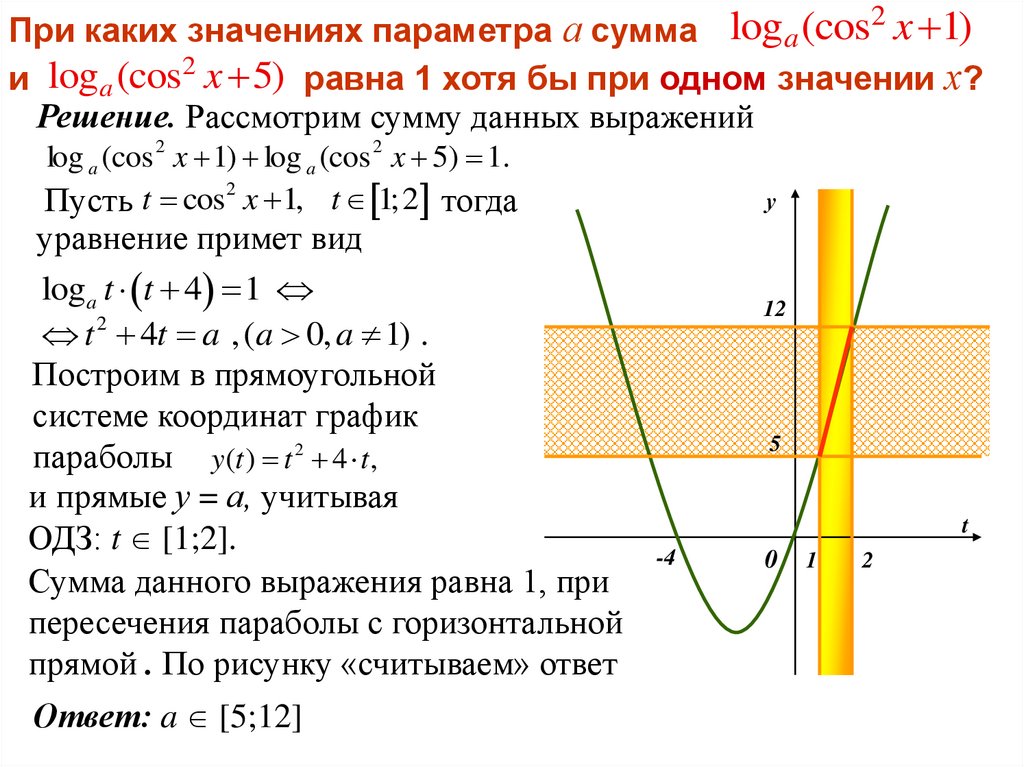
При каких значениях параметра а сумма loga (cos2 x 1)и loga (cos2 x 5) равна 1 хотя бы при одном значении х?
Решение. Рассмотрим сумму данных выражений
log a (cos 2 x 1) log a (cos 2 x 5) 1.
Пусть t cos2 x 1, t 1;2 тогда
уравнение примет вид
loga t t 4 1
t 2 4t a ,(a 0, a 1) .
Построим в прямоугольной
системе координат график
параболы y(t ) t 2 4 t ,
и прямые у = а, учитывая
ОДЗ: t [1;2].
Сумма данного выражения равна 1, при
пересечения параболы с горизонтальной
прямой . По рисунку «считываем» ответ
Ответ: a [5;12]
у
12
5
t
-4
0
1
2
14.
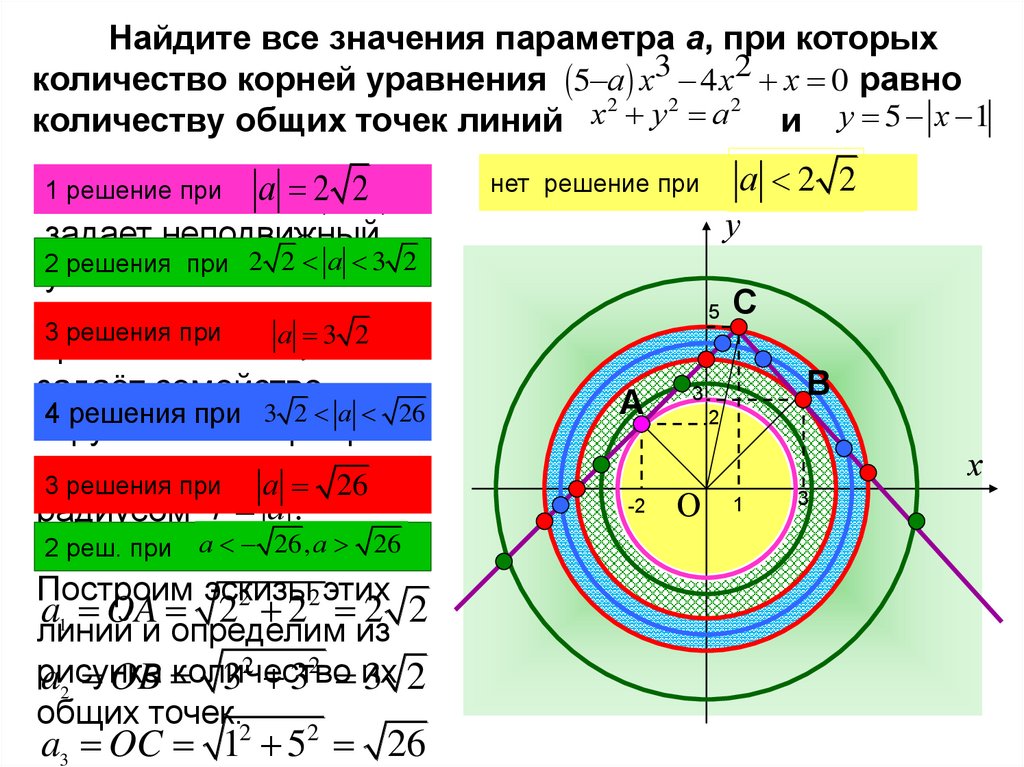
Найдите все значения параметра а, при которыхколичество корней уравнения 5 а х3 4 х2 х 0 равно
2
2
2
х
у
а
количеству общих точек линий
и у 5 х 1
1
решение при
Уравнение
а 5 2х 21
у
задает неподвижный
2 решения при 2 2 а 3
уголок.
у
2
3 решения при
а
х
у 3 2а
Уравнение
задаёт семейство
4 решения при 3 2 а 26
окружностей
с центром
в3 начале
координат
решения при
а 26и
радиусом r а .
2
2 реш. при
2
а 2 2
нет решение при
5
С
2
а 26, a 26
Построим эскизы
2
2 этих
a1 OA 2 2 2 2
линий
и определим из
рисунка
количество
a2 OB
32 32 их
3 2
общих точек.2
2
a3 OC 1 5 26
А
В
3
2
х
-2
О
1
3
15.
Запишем первое уравнение в виде х 5 а х 2 4 х 1 0Заметим, что х = 0 – корень не зависимо от параметра а.
Уравнение 5 а х2 4х 1 0 может иметь 0, 1 или 2 решения
в зависимости от параметра а и дискриминанта D 4 a. 1
одно решение Два решения
первое
уравнение
совокупность
линий
a 1
а = 5; а = 1
Три решения
a 1
а 2 2
3 2 a 2 2, а 3 2, а 26
а 2 2
2 2 a 3 2,
а 3 2,
а 26, a 26
а 26
Осталось заметить, что условие задачи выполняется только
в трех точках при а 2 2, а 3 2 и a 26
Ответ: а 2 2, а 3 2 и a 26
16.
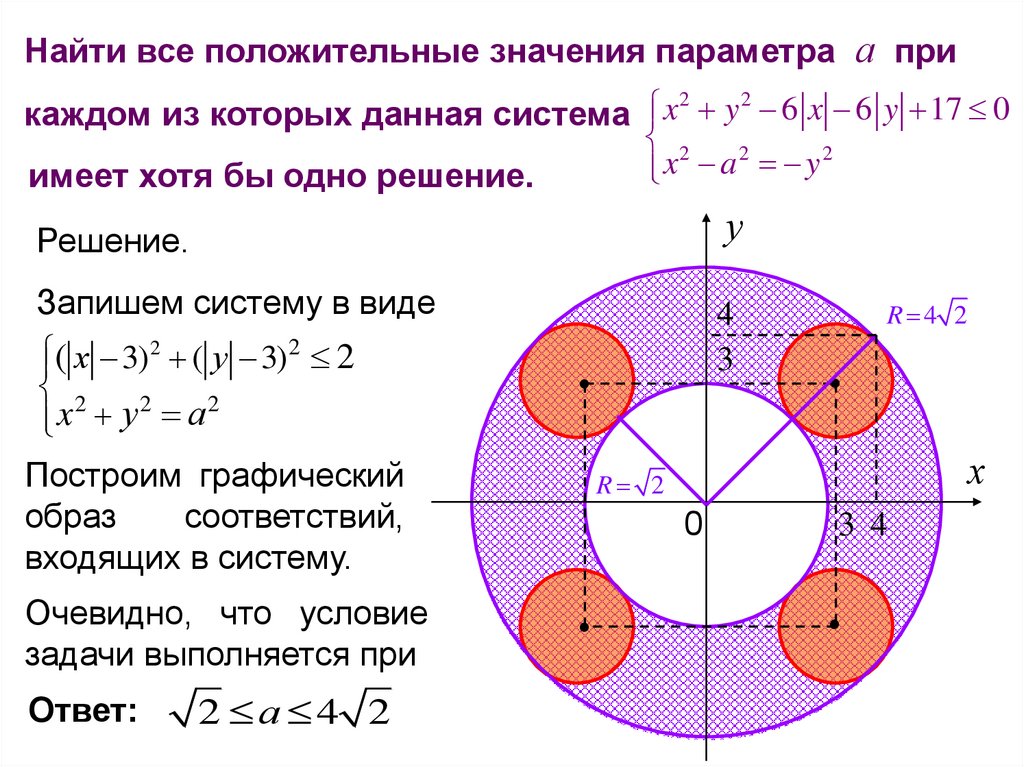
Найти все положительные значения параметра а при2
2
x
y
6 x 6 y 17 0
каждом из которых данная система
2
2
2
x
a
y
имеет хотя бы одно решение.
у
Решение.
Запишем систему в виде
2
2
(
х
3)
(
у
3)
2
2
2
2
x
у
а
Построим графический
образ
соответствий,
входящих в систему.
Очевидно, что условие
задачи выполняется при
Ответ:
2 а 4 2
4
3
R 4 2
х
R 2
0
3 4
17.
Найдите все значения параметра а, для которых прикаждом х из промежутка (4;8] значение выражения
log 22 x 8
не равно значению выражения
(2a 1)log 2 x
Решим задачу при условии равенства данных выражений.
Введем новую переменную
тогда уравнение примет вид:
log2 x t , t 2;3
1
t 2 8 2a 1 t
2
3
График левой части – парабола f (t),
график правой части – прямая g(t).
-4
f (2) 2 8 4, g (2) (2a 1) 2 4, a 1
-8
2
f (3) 32 8 1,
g (3) (2a 1) 3 1,
a 2
3
2
1 2
a ;
2 3
Значит условие исходной задачи выполняется при
1 2
a ; ;
2 3
t
18. Литература
Анимация с сайта: http://badbad-girl.narod.ru/zelenie.htmlЗадачи для решения из книг:
1. Внеурочная работа по математике в контексте реализации
инновационных технологий. Дидактические материалы для
организации деятельности обучаемых: учеб. пособие∕авт.-сост.: А.Т.
Лялькина, Е.В. Чудаева и др. – Саранск, 2007
2. П.И. Горнштейн, В. Б. Полонский, М.С. Якир. Задачи с параметрами.
– М.: Илекса, Харьков: Гимназия, 2003.
3. Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс
подготовки к экзамену. – 6-е изд., - М.: Рольф, 2002.
4. Экзаменационные материалы для подготовки к единому
государственному экзамену. Математика. ЕГЭ – 2007. Составитель:
Клово А.Г. – 2006.







 mathematics
mathematics








