Свойства параллельных прямых (урок 1). Актуализация опорных знаний

1. Тема урока «Свойства параллельных прямых (урок 1)»

2.

Актуализация опорных знаний.

3.

с
а
в

4.

A
D
а) односторонних
B
б) накрест лежащих
в) соответственных
F
C
M
E

5.

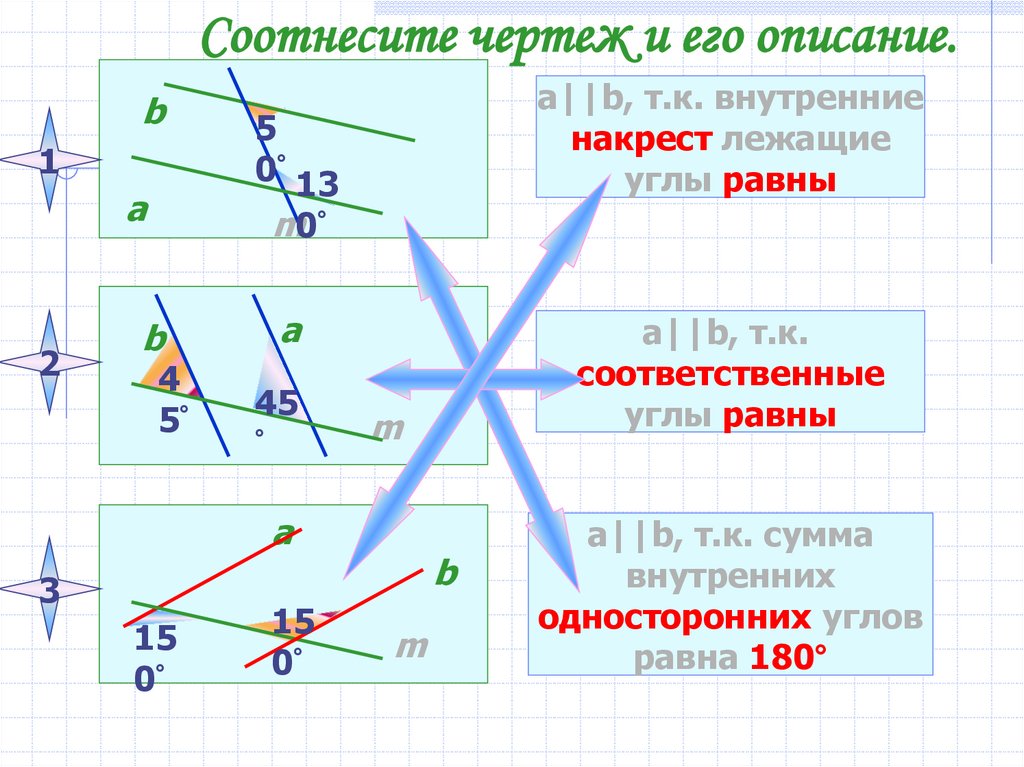
Соотнесите чертеж и его описание.
b
1
a
2
a||b, т.к. внутренние
накрест лежащие
углы равны
5
0° 13
m0°
a
b
4
5°
45
°
m
a
3
15
0°
15
0°
a||b, т.к.
соответственные
углы равны
b
m
a||b, т.к. сумма
внутренних
односторонних углов
равна 180°

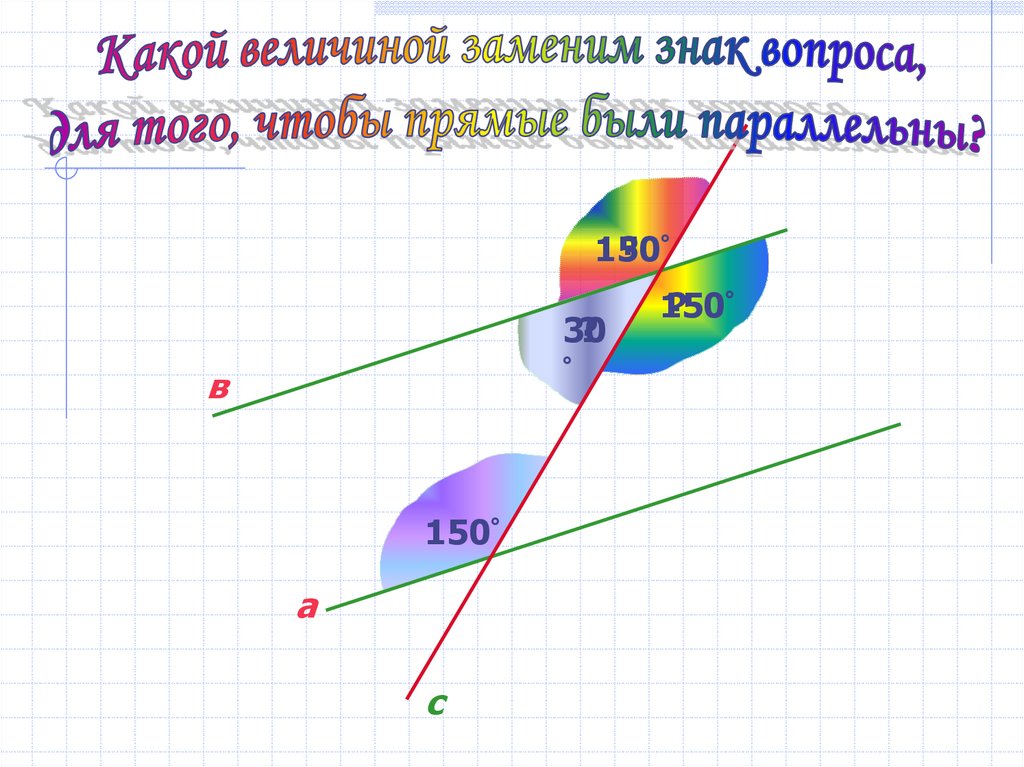
6.

150
? °
30
?
°
в
150°
а
с
150
? °

7.

Признаки параллельности прямых
Если при пересечении двух прямых
секущей накрест лежащие углы равны,
то прямые параллельны.
Если при пересечении двух прямых
секущей соответственные углы равны,
то прямые параллельны.
c
а
1
2
b
c
1
а
2
b
c
Если при пересечении двух прямых
секущей сумма односторонних углов
равна 1800, то прямые параллельны.
а
1
2
b

8.

Введение нового материала.

9.

Если две параллельные прямые пересечены
секущей, то накрест лежащие углы равны.
Дано: a II b, MN- секущая.
Р
1
N
2
M
а
Доказать: 1= 2 (НЛУ)
b
Доказательство:
способ от противного.
Допустим, что 1 2.
Отложим от луча МN угол NМР, равный углу 2.
По построению накрест лежащие углы NМР= 2
РМ II b.
Получили, что через точку М проходит две прямые (а и МР),
параллельные прямой b !!! Это противоречит аксиоме
параллельных прямых. Значит, наше допущение неверно!!!
1= 2.
Теорема доказана.

10.

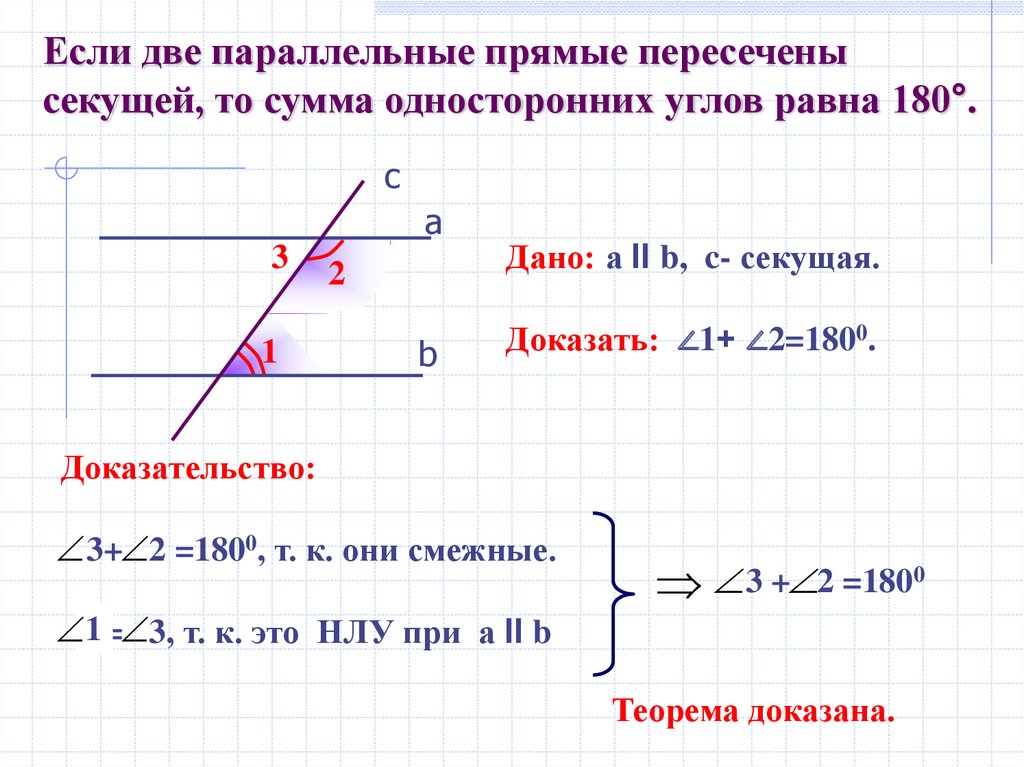
Если две параллельные прямые пересечены
секущей, то сумма односторонних углов равна 180°.
c
а
3
1
2
b
Дано: а II b, c- секущая.
Доказать: ∠1+ ∠2=1800.
Доказательство:
3+ 2 =1800, т. к. они смежные.
11= 3, т. к. это НЛУ при а II b
3 + 2 =1800
Теорема доказана.

11.

Если две параллельные прямые пересечены
секущей, то соответственные углы равны.
c
2
а
3
1
b
Дано: а II b, c- секущая.
Доказать: СУ 1 = 2.
Доказательство:
2 = 3, т. к. они вертикальные.
3 = 1, т. к. это НЛУ при а II b
22
11 = 3 =
Теорема доказана.

12.

Гимнастика для глаз.