Свойства параллельных прямых

1.

05.01.2020
К л а с с н а я р а б о т а.
Свойства параллельных
прямых

2.

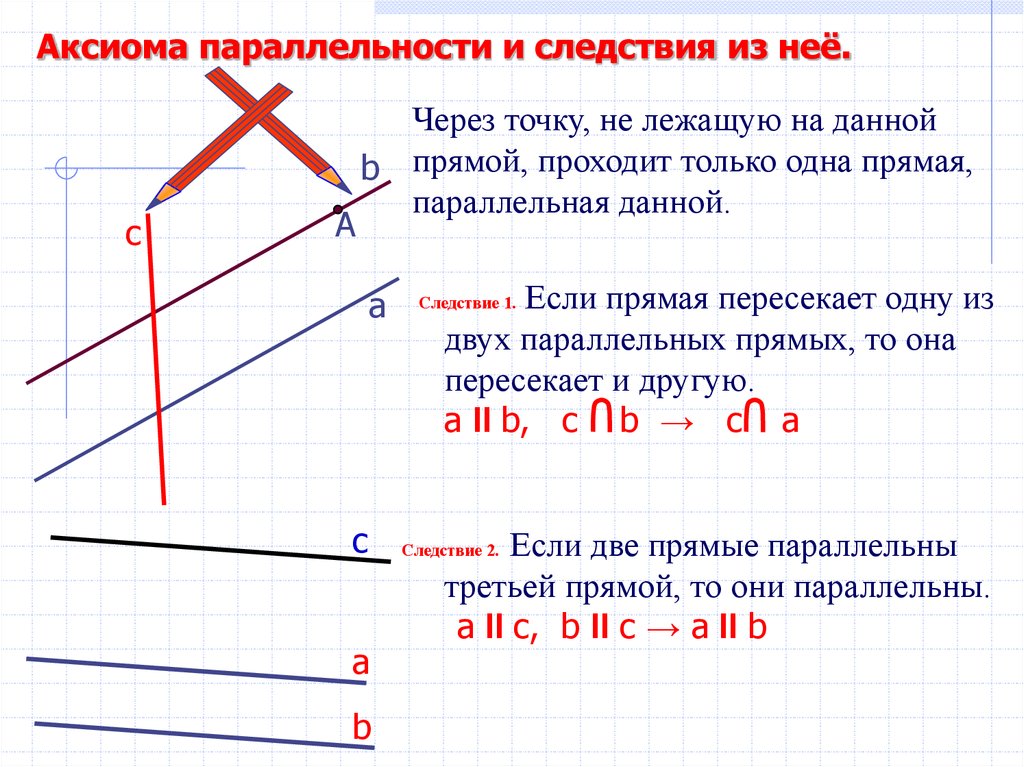
Аксиома параллельности и следствия из неё.
c
А
Через точку, не лежащую на данной
b прямой, проходит только одна прямая,
параллельная данной.
а
с
а
b
Если прямая пересекает одну из
двух параллельных прямых, то она
пересекает и другую.
a II b, c b → c a
Следствие 1.
Если две прямые параллельны
третьей прямой, то они параллельны.
a II с, b II с → a II b
Следствие 2.

3.

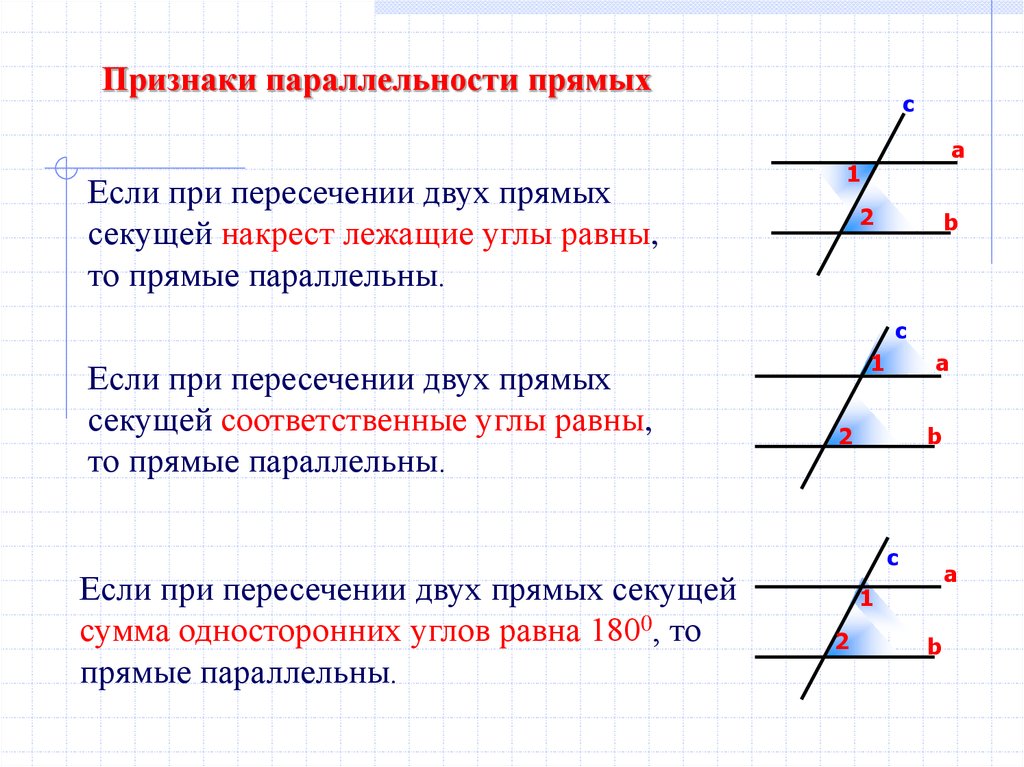
Признаки параллельности прямых
Если при пересечении двух прямых
секущей накрест лежащие углы равны,
то прямые параллельны.
c
а
1
2
b
c
Если при пересечении двух прямых
секущей соответственные углы равны,
то прямые параллельны.
Если при пересечении двух прямых секущей
сумма односторонних углов равна 1800, то
прямые параллельны.
1
а
2
b
c
а
1
2
b

4.

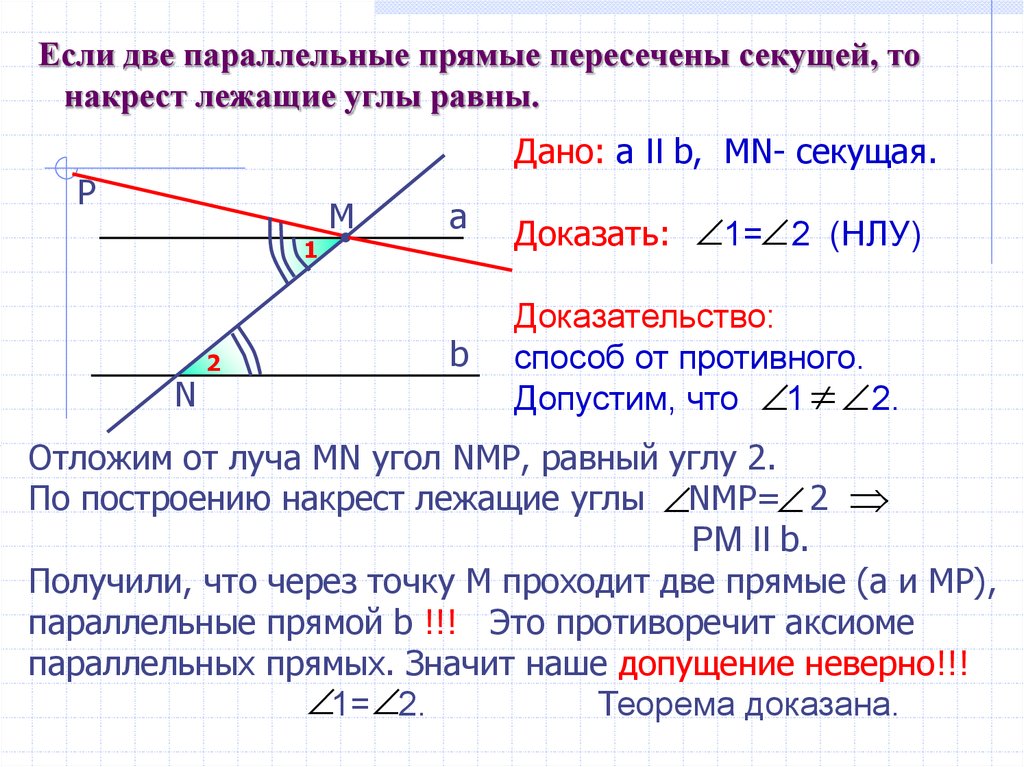
Если две параллельные прямые пересечены секущей, то
накрест лежащие углы равны.
Дано: a II b, MN- секущая.
Р
1
N
2
M
а
Доказать: 1= 2 (НЛУ)
b
Доказательство:
способ от противного.
Допустим, что 1 2.
Отложим от луча МN угол NМР, равный углу 2.
По построению накрест лежащие углы NМР= 2
РМ II b.
Получили, что через точку М проходит две прямые (а и МР),
параллельные прямой b !!! Это противоречит аксиоме
параллельных прямых. Значит наше допущение неверно!!!
1= 2.
Теорема доказана.

5.

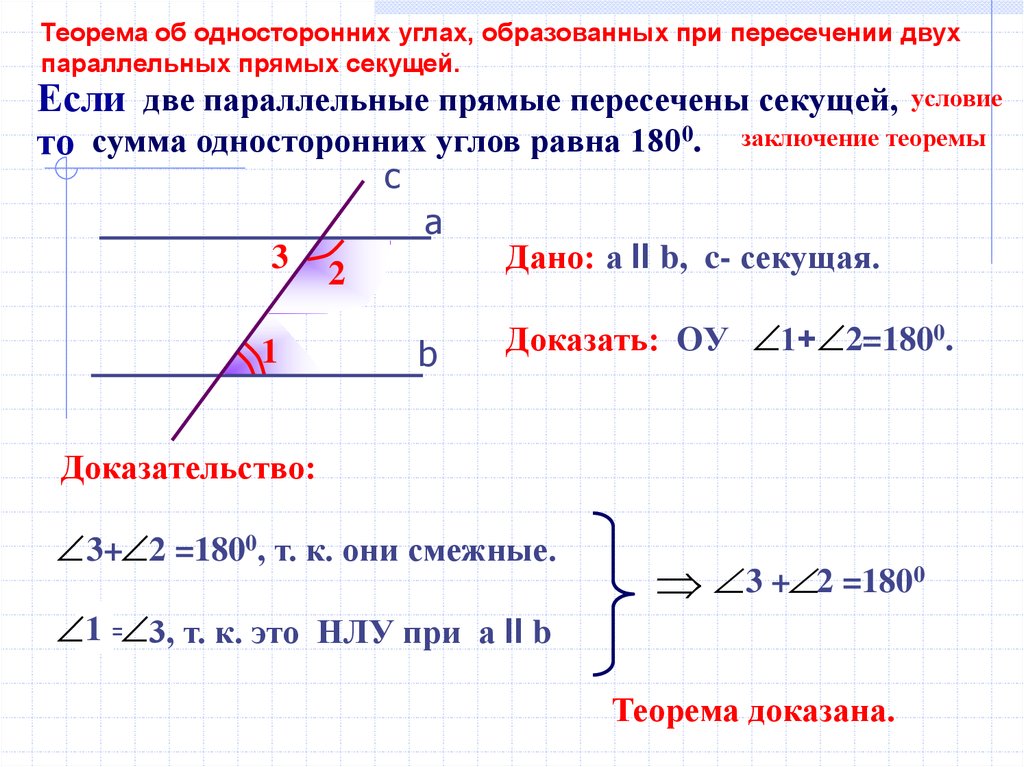
Теорема об односторонних углах, образованных при пересечении двух
параллельных прямых секущей.
Если две параллельные прямые пересечены секущей, условие
то сумма односторонних углов равна 1800.
заключение теоремы
c
а
3
1
2
b
Дано: а II b, c- секущая.
Доказать: OУ 1+ 2=1800.
Доказательство:
3+ 2 =1800, т. к. они смежные.
11= 3, т. к. это НЛУ при а II b
3 + 2 =1800
Теорема доказана.

6.

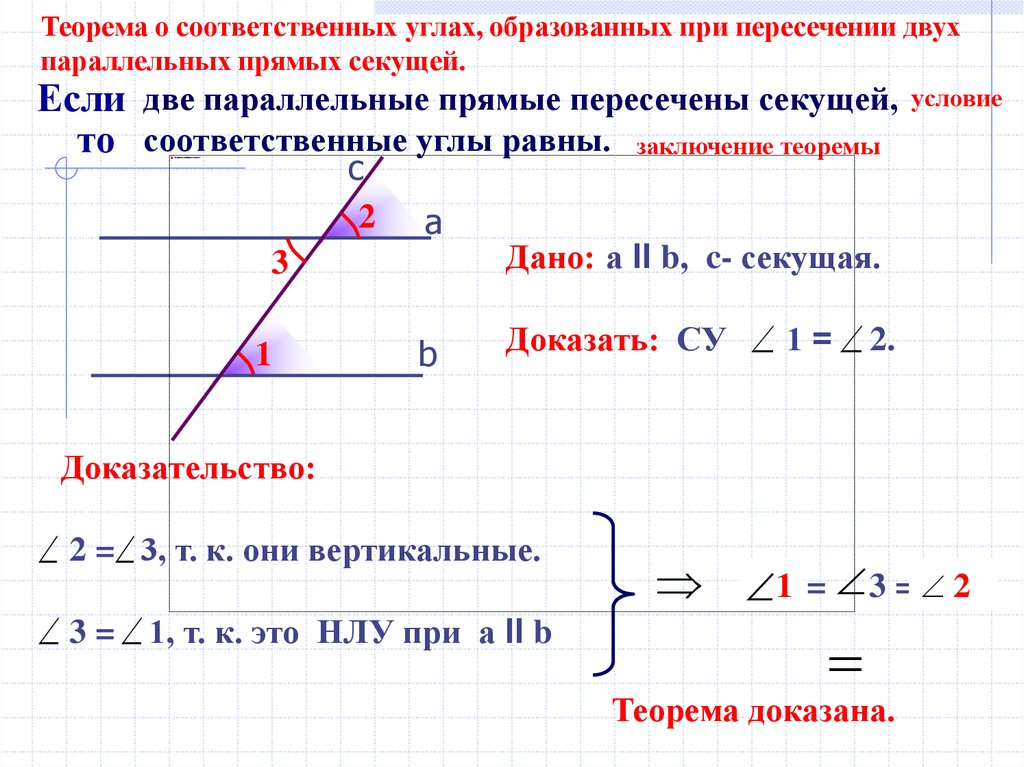
Теорема о соответственных углах, образованных при пересечении двух
параллельных прямых секущей.
Если две параллельные прямые пересечены секущей,
то соответственные углы равны. заключение теоремы
c
2
а
3
1
b
условие
Дано: а II b, c- секущая.
Доказать: СУ 1 = 2.
Доказательство:
2 = 3, т. к. они вертикальные.
3 = 1, т. к. это НЛУ при а II b
11 = 3 =
22
Теорема доказана.

7.

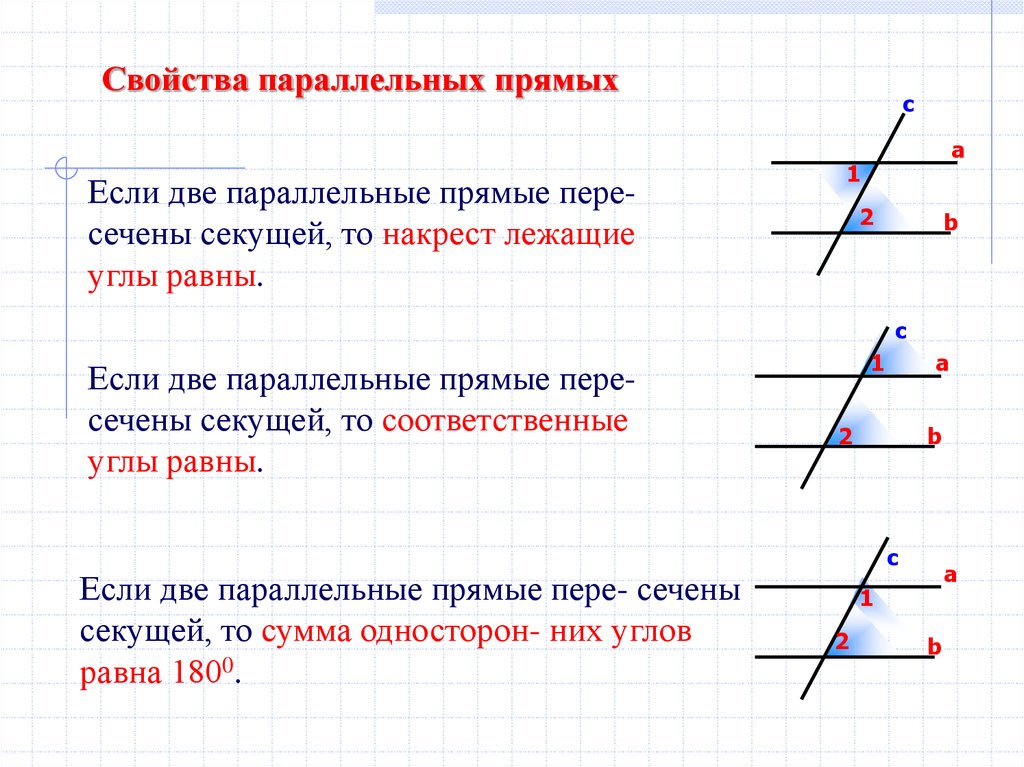
Свойства параллельных прямых
Если две параллельные прямые пересечены секущей, то накрест лежащие
углы равны.
c
а
1
2
b
c
Если две параллельные прямые пересечены секущей, то соответственные
углы равны.
Если две параллельные прямые пере- сечены
секущей, то сумма односторон- них углов
равна 1800.
1
а
2
b
c
а
1
2
b

8.

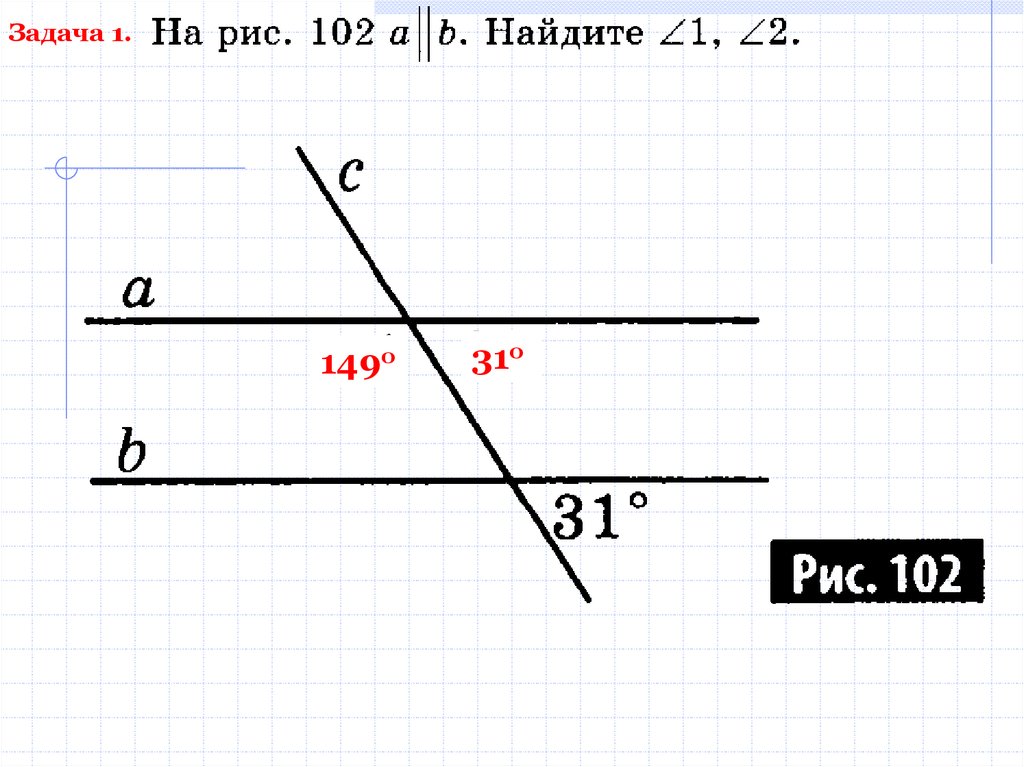
Задача 1.
149о
31о

9.

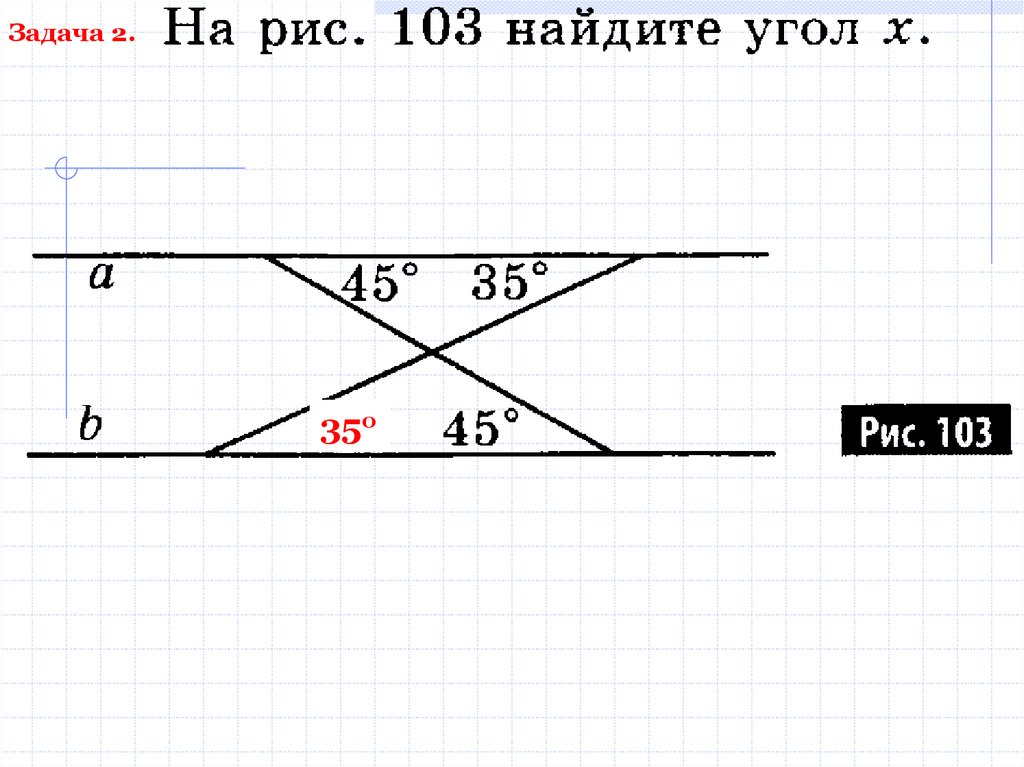
Задача 2.
35о

10.

Задача 3. Две параллельные прямые пересечены третьей. Один из
односторонних углов, образованных при этом, на 58о
больше другого. Найдите эти углы.
с
Дано: а || b, с – секущая,
а
2 - 1 = 58о
2 х + 58
1
х
b
Найти:
1 и 2

11.

Задача 4. Две параллельные прямые пересечены третьей. Один из
односторонних углов, образованных при этом, в три раза
больше другого. Найдите эти углы.
с
Дано: а || b, с – секущая,
а
2 3х
1
х
2 = 3 1
b
Найти:
1 и 2

12.

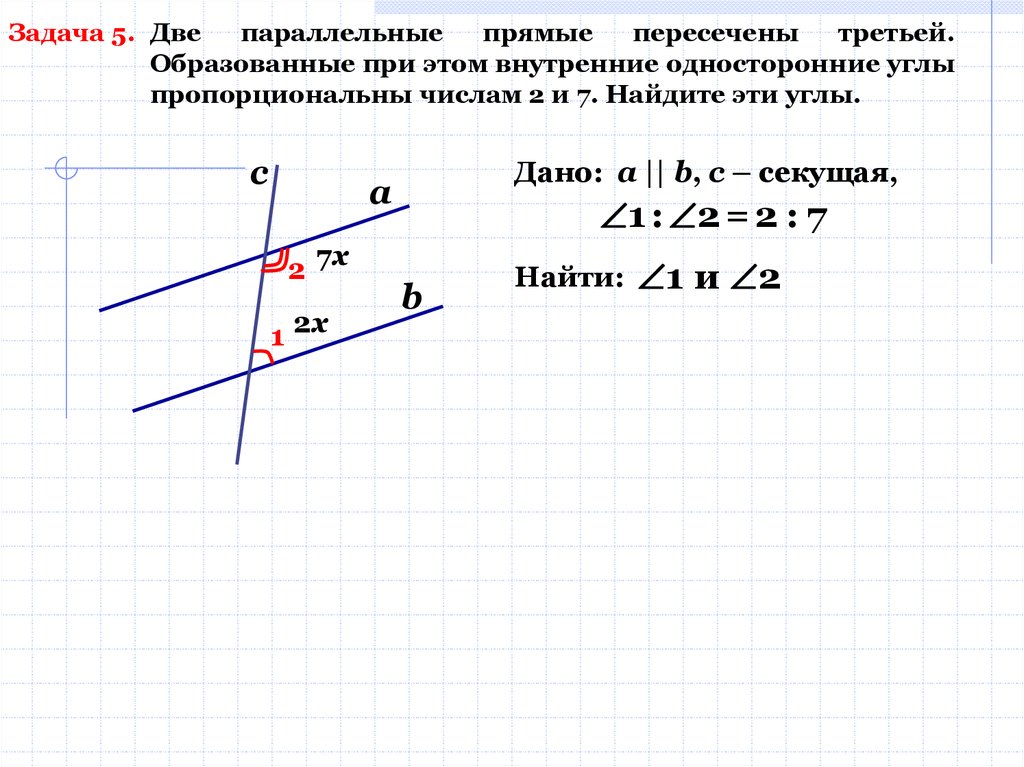
Задача 5. Две
параллельные
прямые
пересечены
третьей.
Образованные при этом внутренние односторонние углы
пропорциональны числам 2 и 7. Найдите эти углы.
с
Дано: а || b, с – секущая,
а
2 7х
1 2х
1 : 2 = 2 : 7
b
Найти:
1 и 2

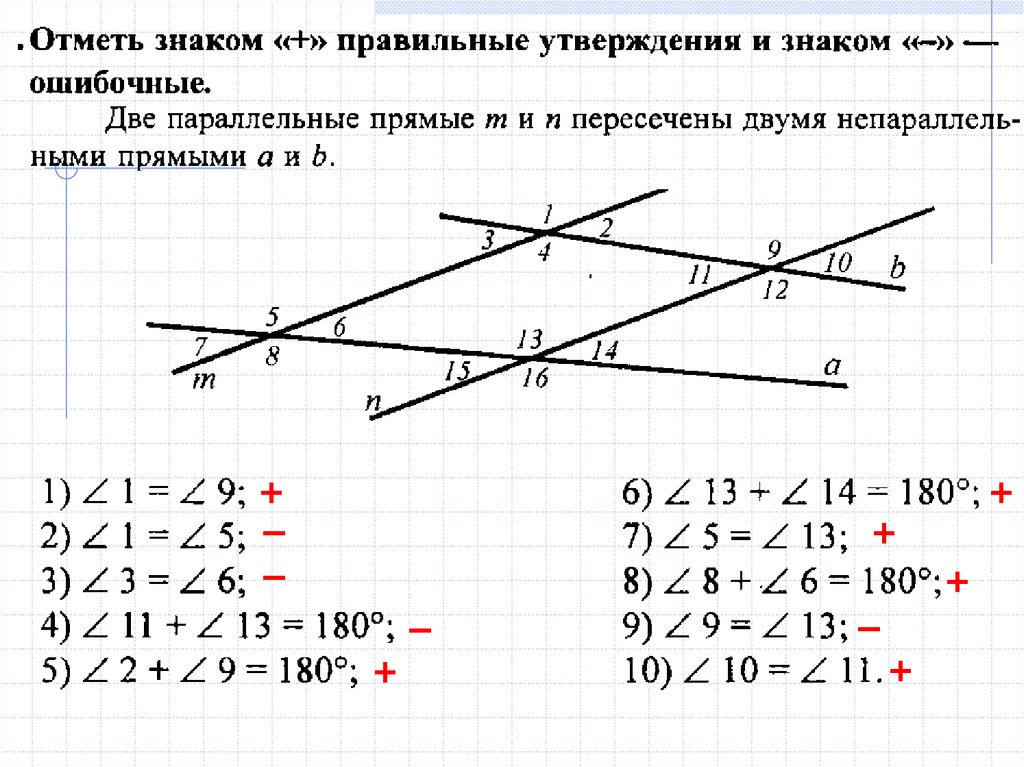
13.

+
–
–
+
+
+
–
+
–
+

14.

п. 27 – 29, вопросы 6 – 15
(устно,
стр.68).
Решить задачи № 203(а), 208.