Перестановки. Розміщення. Комбінації. Алгебра. 11 класс

1. АЛГЕБРА 11

Перестановки.
Розміщення.
Комбінації.

2. Бесіда за питаннями

1. Що послужило поштовхом до
створення комбінаторики ?
2. Які два правила лежать в основі
розв'язання задач комбінаторики?
3. Сформулюйте правила суми та
добутку.

3. Бесіда за питаннями

4. Що називають факторіалом?
5. Як позначають факторіал ?
6. Що вивчає комбінаторика ?
7. Які сполуки вивчає
комбінаторика ?

4. Комбінаторика

Комбінаторика – розділ математики,
у якому вивчають способи вибору та
розташування елементів з деякої
скінченної множини, які
відповідають певним умовам
Вибрані групи елементів називають сполуками
Розміщення
Перестановки
Комбінації

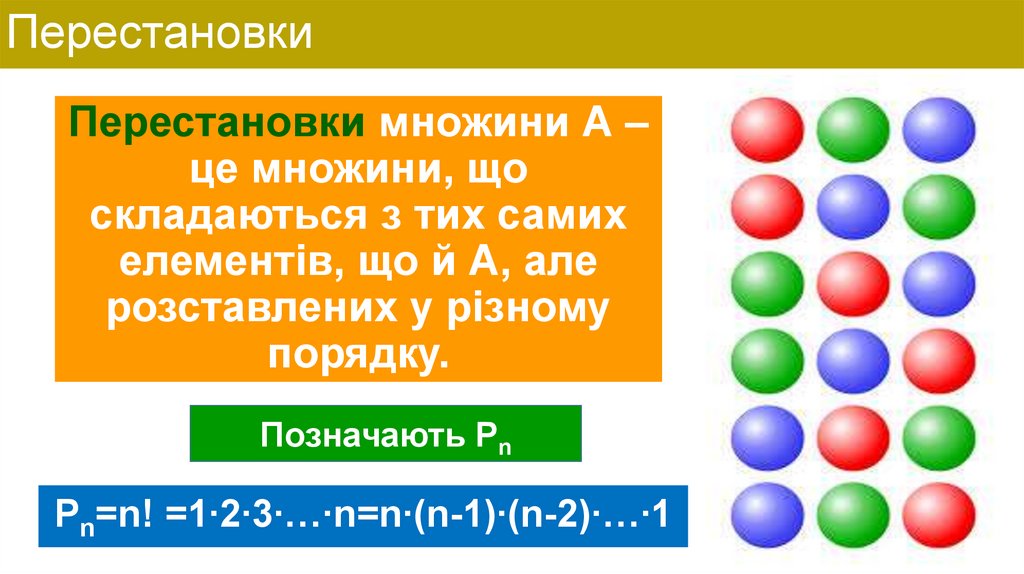
5. Перестановки

Перестановки множини А –
це множини, що
складаються з тих самих
елементів, що й А, але
розставлених у різному
порядку.
Позначають Pn
Pn=n! =1∙2∙3∙…∙n=n∙(n-1)∙(n-2)∙…∙1

6. Розв'язування задач

Скількома
способами можна
розставити на
полиці 7 книжок?
Р7 = 7! = 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 = 5040

7. Розв'язування задач

Скільки різних чотирицифрових чисел можна
скласти з цифр 0; 1; 2; 3, якщо в кожному числі
жодна з цифр не повторюється?
1. З чотирьох цифр 0; 1;
2; 3 можна утворити Р4
перестановок.
2. Відняти ті, які
починаються з 0 - Р3.
Отже, шукана кількість чотирицифрових чисел
дорівнює: N= Р4 - Р3 = 4! - 3! = 3!(4 - 1) = 6 ∙ 3 = 18.

8. Розміщення

Будь-яка впорядкована
підмножина з m елементів
даної n-елементної
множини називається
розміщенням з n
елементів по m.

9. Розв'язування задач

Розклад на день
містить 6 уроків.
Визначити кількість
всіх можливих
розкладів при виборі з
9 предметів, при умові,
що жоден предмет не
стоїть у розкладі двічі.

10. Комбінації

Комбінацією з n
елементів по m
називається будь-яка
невпорядкована m елементна підмножина
даної n - елементної
множини.

11. Розв'язування задач

У вазі 8 червоних і 3 білих
троянди. Скількома
способами з вази можна
вибрати: 1) три троянди;
2) дві червоні і одну білу
троянду?

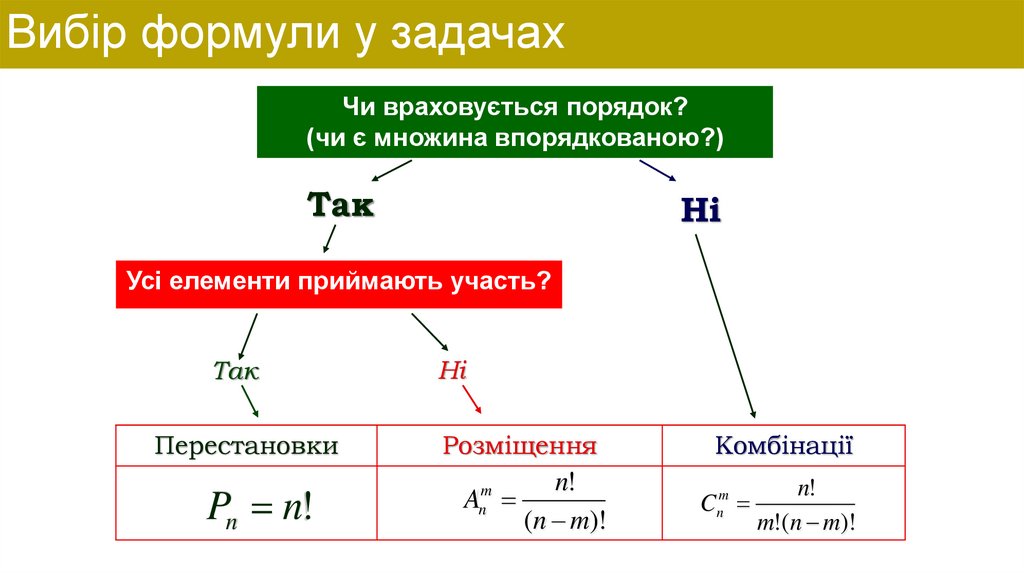
12. Вибір формули у задачах

Чи враховується порядок?
(чи є множина впорядкованою?)
Так
Ні
Усі елементи приймають участь?
Так
Ні
Перестановки
Розміщення
Pn n!
n!
A
(n m)!
m
n
Комбінації
Cnm
n!
m!(n m)!

13. Розв'язування задач

З 30 учнів класу треба вибрати
відповідальних за дисципліну і
навчання. Скількома способами
це можна зробити?
870
30!
1
5
435
Інша
відповід
ь

14. Розв'язування задач

Скількома способами
можна вибрати трьох
чергових з групи в 20
чоловік?
6
20!
114
0
6840
Інша
відповідь

15. Розв'язування задач

Скількома способами
можна вісім учнів
вишикувати в колону по
одному?
8
64
256
40320
Інша
відповід
ь

16. Розв'язування задач

У коробці знаходяться 10 синіх і
6 червоних куль. Скількома
способами з коробки можна
витягти одну кулю будь-якого
кольору?
60
10
6
16
Інша
відповідь

17. Розв'язування задач

Маємо чотири різні конверти без
марок і три різні марки. Скількома
способами можна вибрати
конверт і марку для відправки
листа?
3
4
7
12
Інша
відповідь

18. Бесіда за питаннями

1. Які види сполук ви знаєте ?
2. Що називають перестановкою? За
якою формулою обчислюють?
3. Що називають розміщеннями ? За
якою формулою обчислюють ?
4. Що називають комбінаціями ? За
якою формулою обчислюють ?

19.

Домашнє завдання
Опрацювати §14
Виконати вправи № 14.16, 14.20,
14.39, 14.54