Комбінаторні правила суми та добутку

1.

Матеріали уроку
«Комбінаторні правила суми та добутку»
(А.Мерзляк, Д.Номіровський, В.Полонський, М.Якір),
п. 13

2.

ЕЛЕМЕНТИ КОМБІНАТОРИКИ,
ТЕОРІЇ ЙМОВІРНОСТЕЙ І
СТАТИСТИКИ
Комбінаторні
правила
суми
та добутку

3.

Комбінаторика – розділ математики, який вивчає способи
розв’язування задач про вибір і розміщення елементів деякої
множини на основі якихось умов.
Термін «комбінаторика» ввів Готфрід Вільгельм Лейбніц —
провідний німецький філософ, логік, математик, фізик,
мовознавець та дипломат. Передбачив принципи сучасної
комбінаторики.
Підґрунтям для розв’язування більшості
комбінаторних задач
є два правила:
правило суми та правило добутку

4.

Приклад 1
Деякий учень проживає від школи на певній відстані. До його
мікрорайону
можна добратися зі школи 2 автобусами або, навпростець, 3 безпечними
шляхами. Скількома способами учень може вибрати дорогу додому?
Розв'язання
Оскільки всього є 2 + 3 = 5 шляхів додому, то, очевидно, відповідь:
5 способів вибору шляху.

5.

Приклад 2
На столі у секретаря лежать 12 олівців та 7 ручок. Для запису
термінової інформації секретар навмання вибирає олівець або ручку.
Скількома способами він може це зробити?
Розв'язання
12+7 = 19
Відповідь: 19 способів

6.

Приклад 3
Скільки можна скласти чотирицифрових кодів для банківської картки?
Розв'язання
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Кількість способів скласти код:
_∙ _∙ _∙ _-?
10 ∙ 10 ∙ 10 ∙ 10 = 10 4 = 10 000
Відповідь: 10 000 варіантів кодів

7.

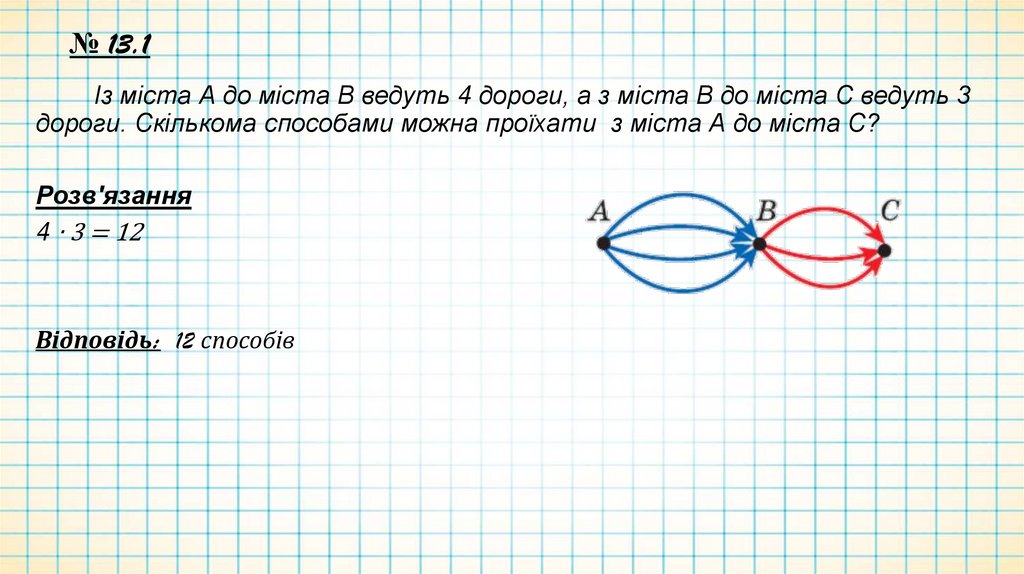
№ 13.1
Із міста А до міста В ведуть 4 дороги, а з міста В до міста С ведуть 3
дороги. Скількома способами можна проїхати з міста А до міста С?
Розв'язання
4 ∙ 3 = 12
Відповідь: 12 способів

8.

Розв'язування вправ
№ 13.3
Розглядатимемо склади з двох букв, перша з яких позначає приголосний
звук, а друга — голосний. Скільки таких різних складів можна скласти з букв
слова:
1) шабля;
2) шаровари?
Розв'язання
1) У слові «шабля» 3 різних приголосних та 2 різні голосні літери, тому
3∙2= 6
2) У слові «шаровари» 3 різних приголосних та 3 різні голосні літери, тому
3∙3= 9
Відповідь: 1) 6 складів; 2) 9 складів

9.

№ 13.4
У корзині лежать 10 яблук і 7 груш. Антон вибирає яблуко або
грушу. Після цього Максим вибирає яблуко та грушу. У якому випадку
Максим має більше можливостей для вибору: коли Антон узяв
яблуко чи коли Антон узяв грушу?
Розв'язання
1) Нехай Антон вибрав яблуко. Тоді Максиму залишається
9 яблук та 7 груш. Тоді у нього кількість способів для вибору обох фруктів:
9 ∙ 7 = 63
2) Якщо ж Антон вибрав грушу, тоді Максиму залишається 10 яблук та 6
груш.
Тоді кількість способів для вибору обох фруктів:
10 ∙ 6 = 60
Зрозуміло, що 63 > 60.
Відповідь: Максим має більше можливостей для вибору, якщо Антон візьме
яблуко

10.

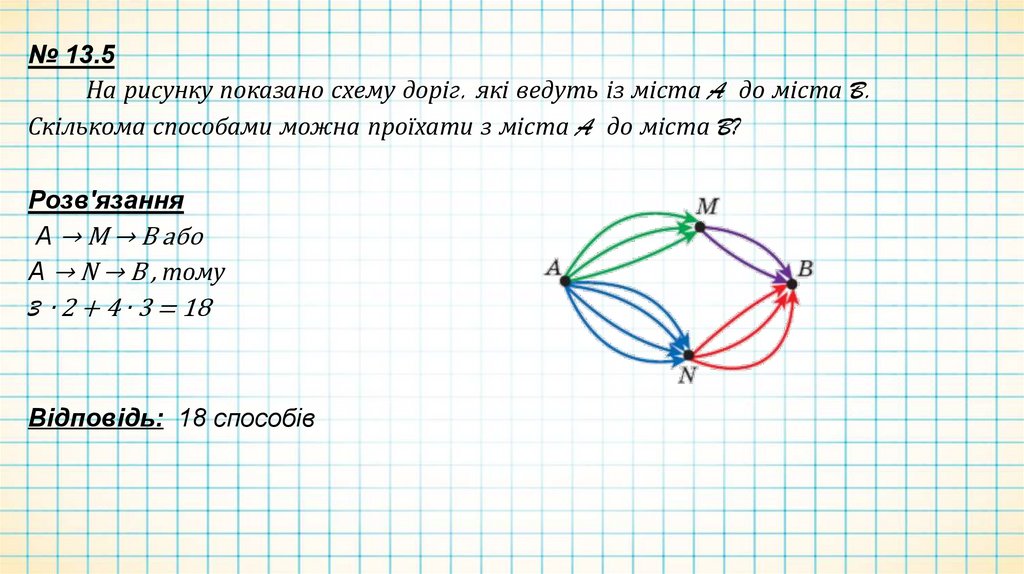
№ 13.5
На рисунку показано схему доріг, які ведуть із міста A до міста B.
Скількома способами можна проїхати з міста A до міста B?
Розв'язання
А → М → В або
А → N → В , тому
3 ∙ 2 + 4 ∙ 3 = 18
Відповідь: 18 способів

11.

Розв'яжіть, будь ласка, самостійно: № 13.2,
№ 13.2
Кафе пропонує в меню 3 перші страви, 6 других страв і 5 третіх
страв. Скільки існує способів вибрати обід із трьох страв (по одній страві
кожного виду)?
Розв'язання
3 ∙ 6 ∙ 5 = 90
Відповідь: 90 способів

12.

Рекомендую виконати самостійно: № 13.6, 13.11, 13.14.
ДЯКУЮ ЗА УВАГУ!
ДО ПОБАЧЕННЯ!