Similar presentations:
Квадратичная функция, её график и свойства
1.
Квадратичнаяфункция, её график и
свойства.
Презентация подготовлена
Бех О.Н.,
учителем математики
МБОУ СОШ №24
2.
Цели:• повторить свойства квадратичной
функции;
• закрепить их знание при построении
графиков квадратичной функции;
• подготовка к государственной
(итоговой) аттестации
3.
Тест1. Функция вида y = ax² + bx + c, где a, b и c – … числа, … ≠ 0,
x – … переменная, называется … функцией.
2. Значения x, при которых квадратичная функция y (x) = 0,
называются … этой функции.
3. Кривая, являющаяся графиком функции y = ax² + bx + c,
называется … .
4. График функции y = x² симметричен относительно оси … .
5. Точку пересечения параболы с её осью … называют … … .
6. Функция y = x² является … на промежутке x ≥ 0 и убывающей
на промежутке x…0 .
7. При a … 0 ветви параболы y = ax² + bx + c направлены вверх,
а при a … 0 – вниз.
8. Координаты вершины параболы y = ax² + bx + c можно найти
по формулам: m = - ― ,
n = y(m) = a … + b … + c.
4.
Тест1. Функция вида y=ax² + bx + c, где a, b и c – некоторые числа, a≠0,
x – независимая переменная, называется квадратичной
функцией.
2. Значения x, при которых квадратичная функция y (x) = 0,
называются нулями этой функции.
3. Кривая, являющаяся графиком функции y = ax² + bx + c,
называется параболой.
4. График функции y = x² симметричен относительно оси y.
5. Точку пересечения параболы с её осью симметрии называют
вершиной параболы .
6. Функция y = x² является возрастающей на промежутке x ≥ 0 и
убывающей на промежутке x ≤ 0 .
7. При a > 0 ветви параболы y = ax² + bx + c направлены вверх, а
при a < 0 – вниз.
8. Координаты вершины параболы y = ax² + bx + c можно найти по
b
формулам: m = , n = y(m) = am² + bm + c.
2a
5.
Прочитайте графикУ
9
4
1
-1
1
2
3
Х
6.
Выполните заданияЗадание 1
У
• Определите, график
какой функции
изображен на рисунке
А. у = - (х-3)2 + 1
Б. у = (х+3) 2 - 1
В. у = (х-1) 2 + 3
-3
-1
Х
7.
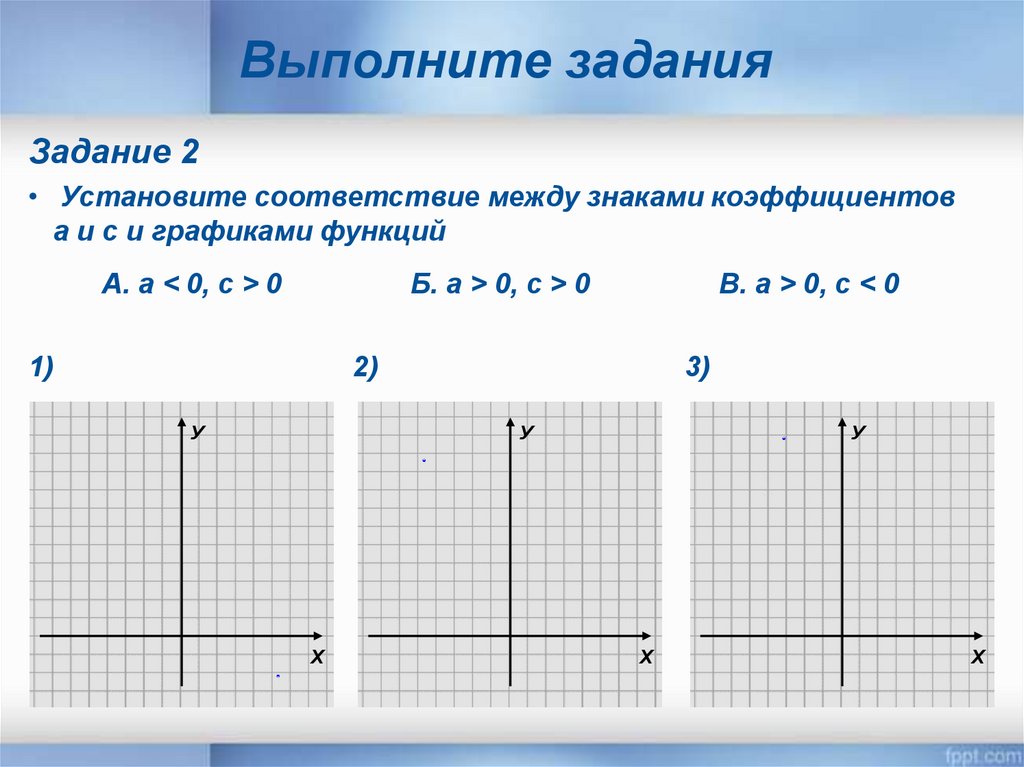
Выполните заданияЗадание 2
• Установите соответствие между знаками коэффициентов
a и c и графиками функций
А. а < 0, c > 0
Б. а > 0, c > 0
1)
В. а > 0, c < 0
2)
У
3)
У
Х
У
Х
Х
8.
Выполните заданияЗадание 3
• Установите соответствие между графиками функций и
формулами, которые их задают
1) у = х2 - 7х + 9
2) у = - х2 - 7х - 9
А)
3) у = - х2 + 7х - 9
Б)
В)
У
У
У
Х
Х
Х
9.
Повторим• Восстановите алгоритм построения графика квадратичной
функции
Найти координаты
вершины параболы и
отметить её в
координатной
плоскости
Провести через
вершину параболы
прямую,
параллельную оси
OY – ось симметрии
параболы
Соединить
отмеченные точки
плавной
линией
Построить ещё
несколько точек,
принадлежащих
параболе
10.
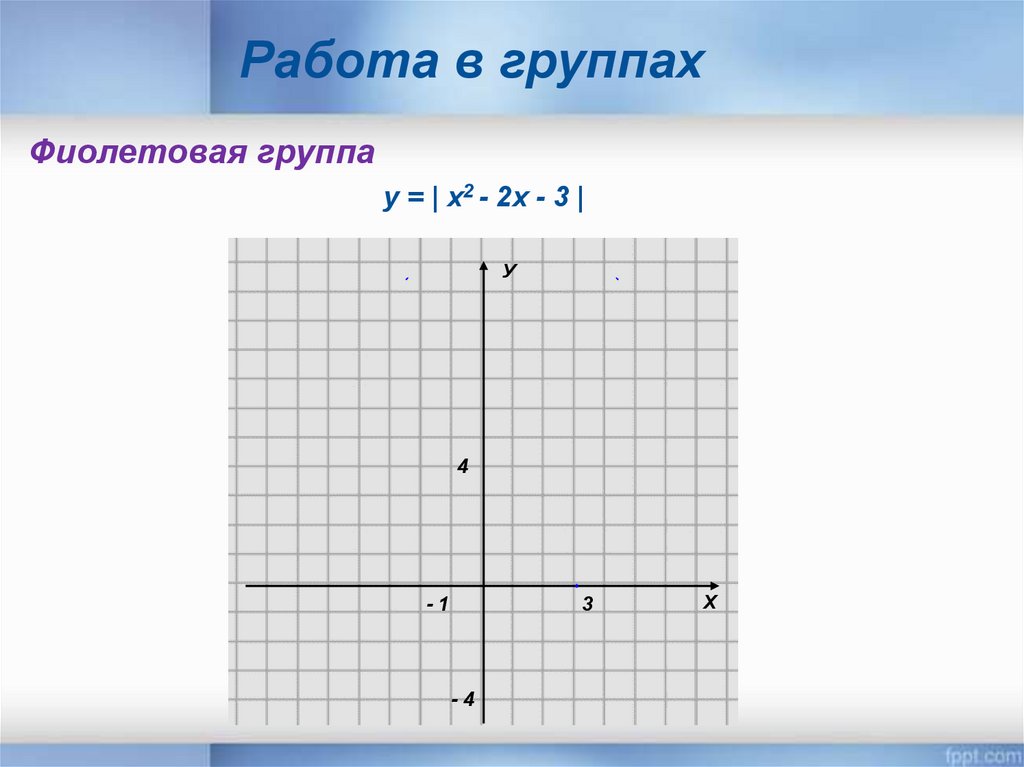
Работа в группахФиолетовая группа
у = | х2 - 2х - 3 |
У
4
-1
3
-4
Х
11.
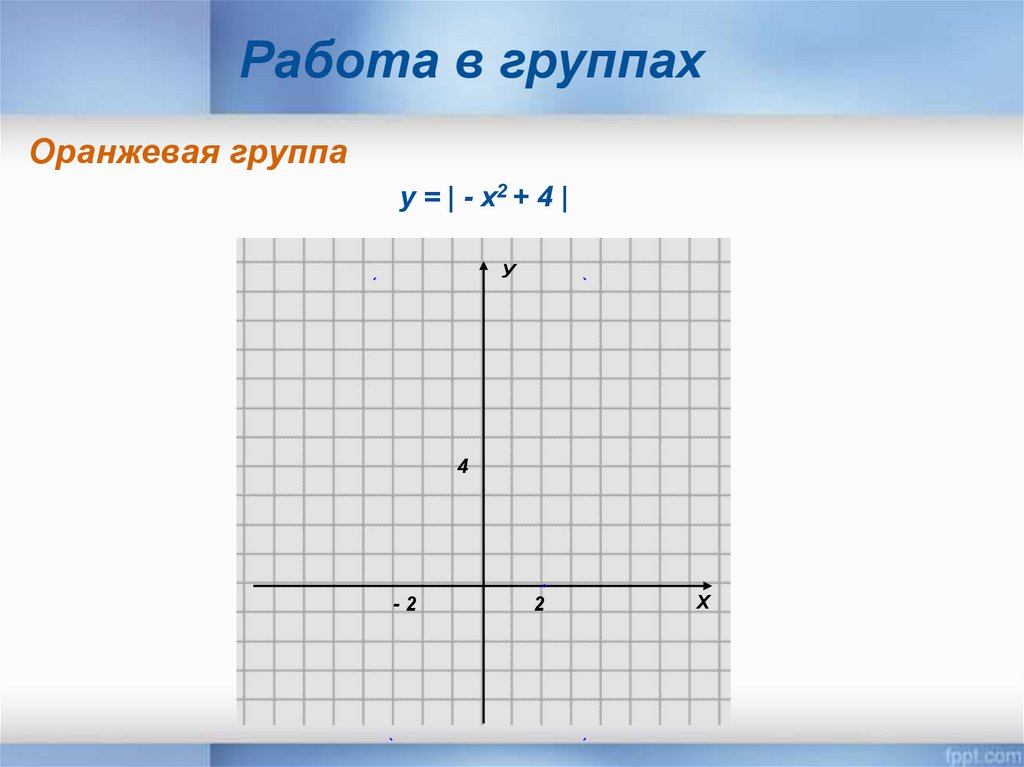
Работа в группахОранжевая группа
у = | - х2 + 4 |
У
4
-2
2
Х
12.
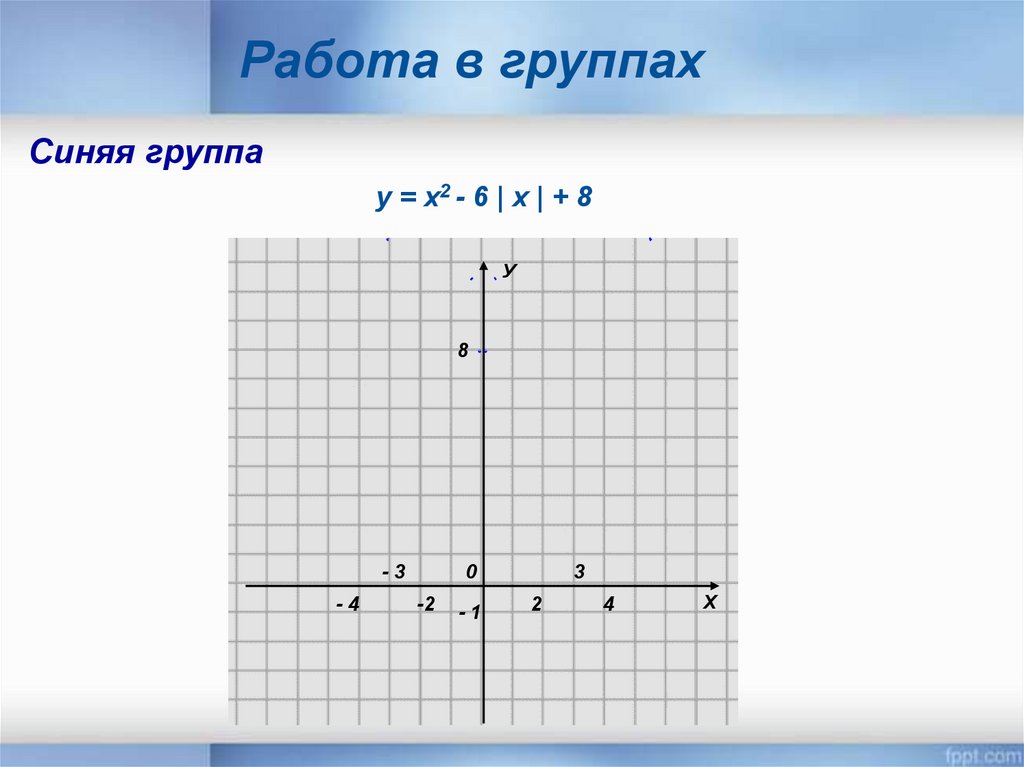
Работа в группахСиняя группа
у = х2 - 6 | х | + 8
У
8
-3
-4
0
-2
-1
3
2
4
Х
13.
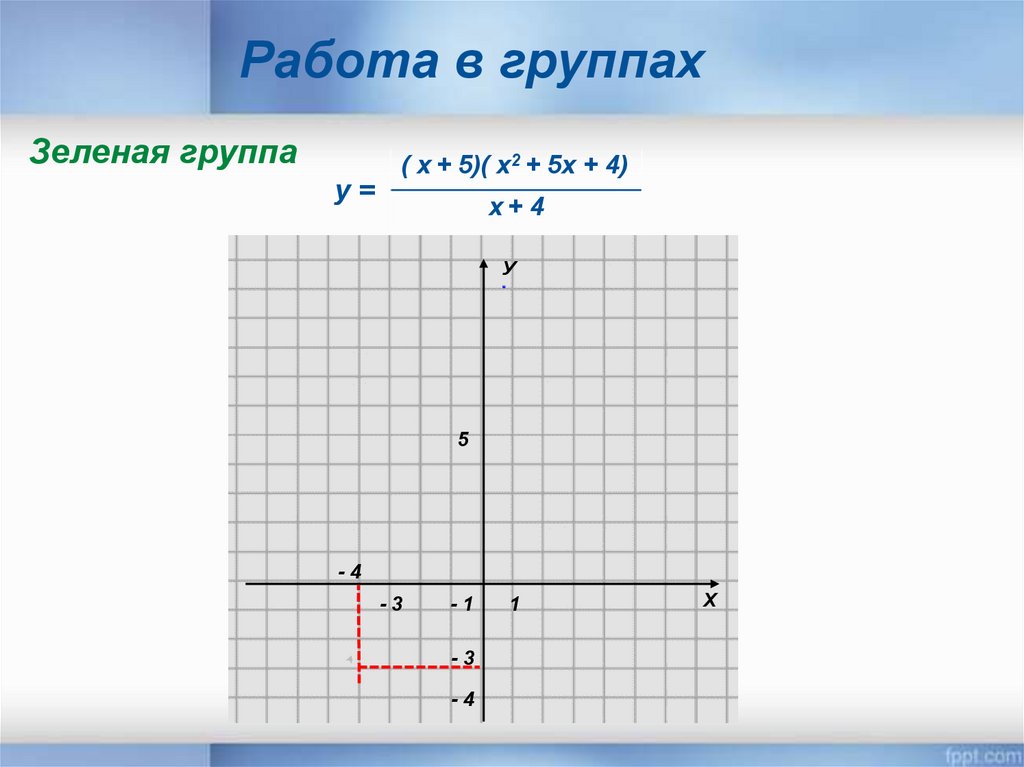
Работа в группахЗеленая группа
у=
( х + 5)( х2 + 5х + 4)
х+ 4
У
5
-4
-3
-1
-3
-4
1
Х
14.
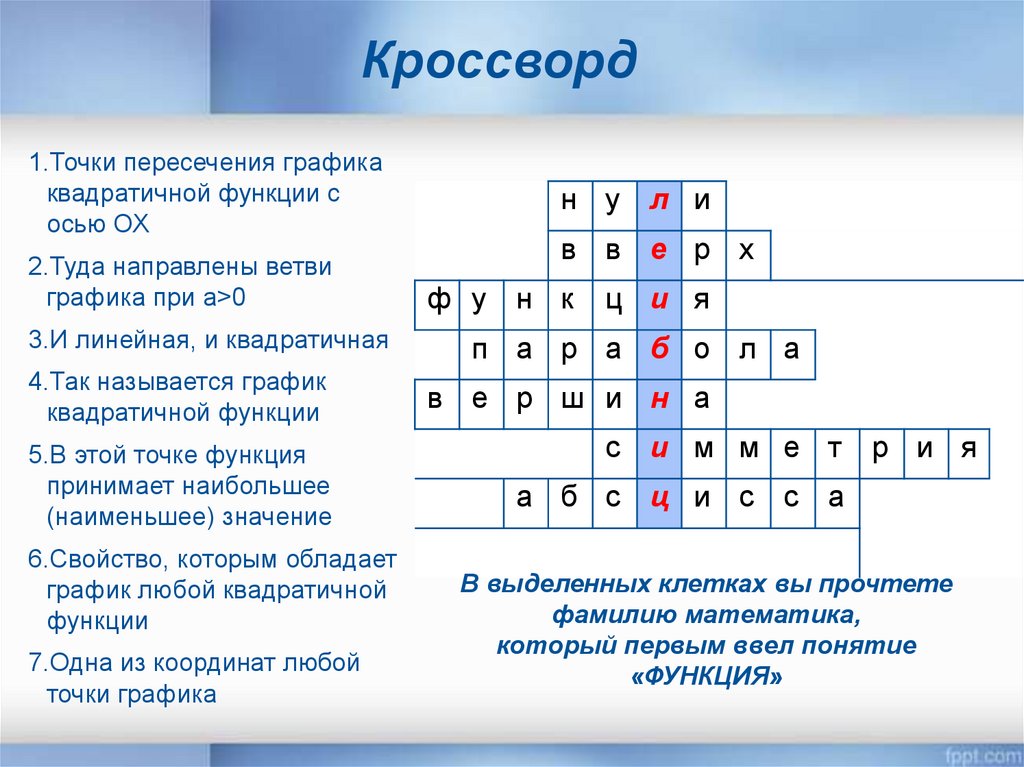
Кроссворд1.Точки пересечения графика
квадратичной функции с
осью ОХ
2.Туда направлены ветви
графика при а>0
1
2
3
4
3.И линейная, и квадратичная
4.Так называется график
квадратичной функции
5.В этой точке функция
принимает наибольшее
(наименьшее) значение
6.Свойство, которым обладает
график любой квадратичной
функции
7.Одна из координат любой
точки графика
5
6
7
В выделенных клетках вы прочтете
фамилию математика,
который первым ввел понятие
«ФУНКЦИЯ»
15.
Кроссворд1.Точки пересечения графика
квадратичной функции с
осью ОХ
2.Туда направлены ветви
графика при а>0
3.И линейная, и квадратичная
4.Так называется график
квадратичной функции
5.В этой точке функция
принимает наибольшее
(наименьшее) значение
6.Свойство, которым обладает
график любой квадратичной
функции
7.Одна из координат любой
точки графика
н у л и
в в е р х
ф у н к
ц и я
п а р а б о л а
в е р ш и н а
с и м м е т
р и я
а б с ц и с с а
В выделенных клетках вы прочтете
фамилию математика,
который первым ввел понятие
«ФУНКЦИЯ»
16.
Великий математикСаксонский математик,
философ, логик, механик,
физик, юрист, историк,
дипломат,
изобретатель и языковед.
Основатель
дифференциального и
интегрального исчислений.
Готфрид Вильгельм
Лейбниц
(1646-1716)
17.
Домашнее задание• выберите одно из заданий с функцией,
график которой вы хотите построить
1. Постройте график функции у = | х2 - х - 2 |. Какое наибольшее число
общих точек график данной функции может иметь с прямой,
параллельной оси абсцисс?
2. Постройте график функции у = | 2х2 – 6 |х| + 4 |
3. Постройте график функции у = х2 – | 2х + 1 | и определите, при каких
значениях m прямая у = m имеет с графиком ровно три общие точки
4. Постройте график функции у = х2 - 2х - 15. Перечисли свойства.
• творческое задание
подготовить сообщение о Лейбнице












 mathematics
mathematics








