Сложение векторов. Правило треугольника. Подготовка к контрольной работе

1.

05.02.2024
К л а с с н а я р а б о т а.
Подготовка к контрольной
работе.

2.

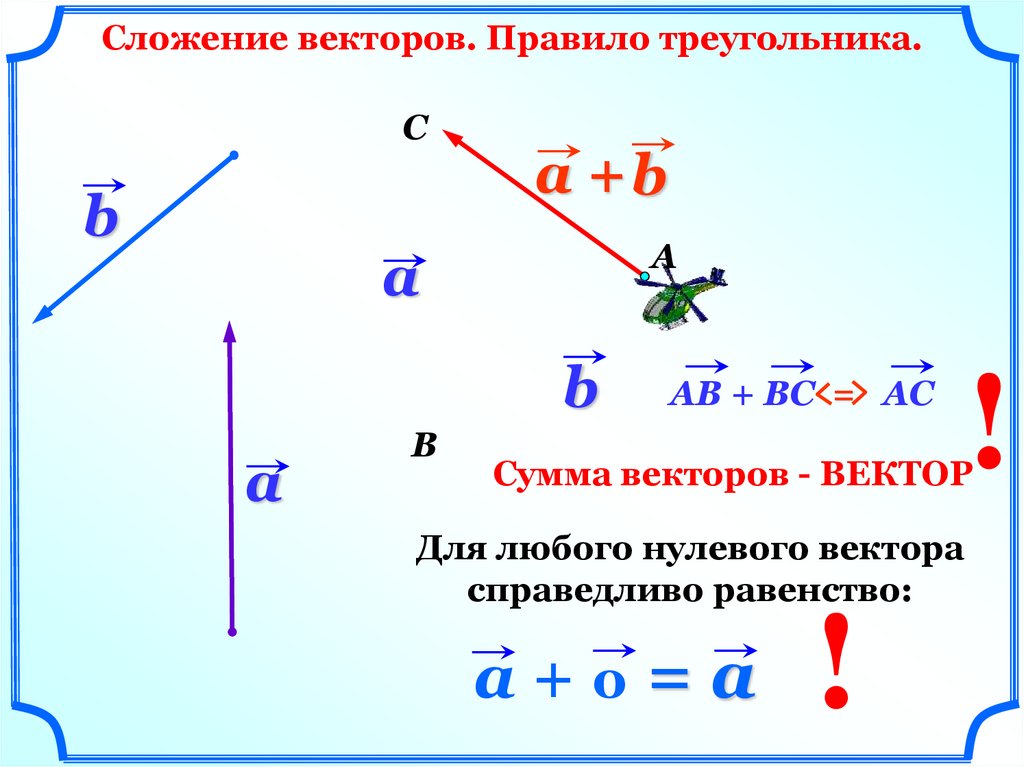
Сложение векторов. Правило треугольника.
C
b
a +b
A
a
b
a
B
AB + BC = AC
!
Сумма векторов - ВЕКТОР
Для любого нулевого вектора
справедливо равенство:
a+0=a
!

3.

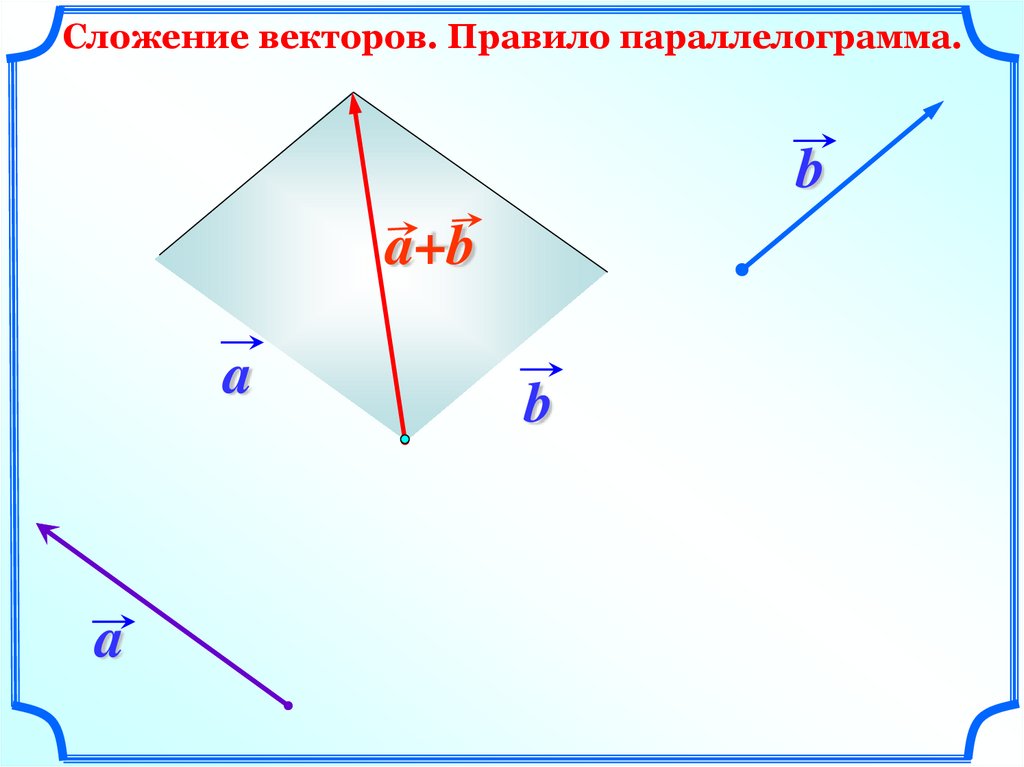
Сложение векторов. Правило параллелограмма.
b
a+b
a
a
b

4.

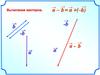
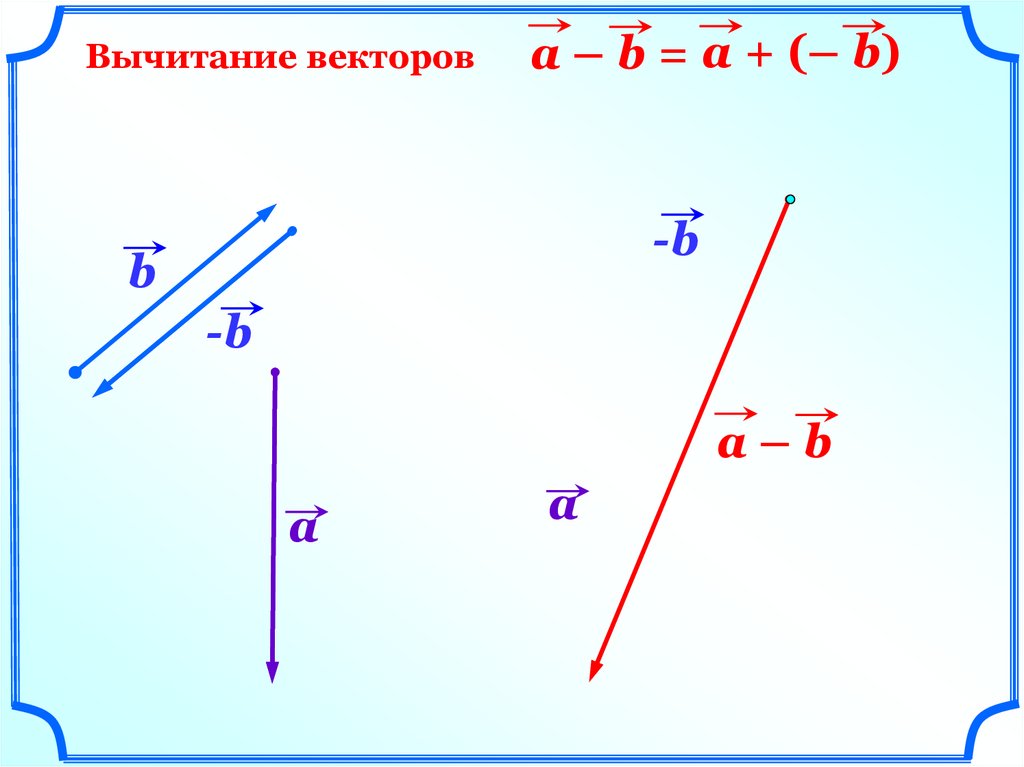
Вычитание векторов
а – b = а + (– b)
-b
b
-b
а–b
a
a

5.

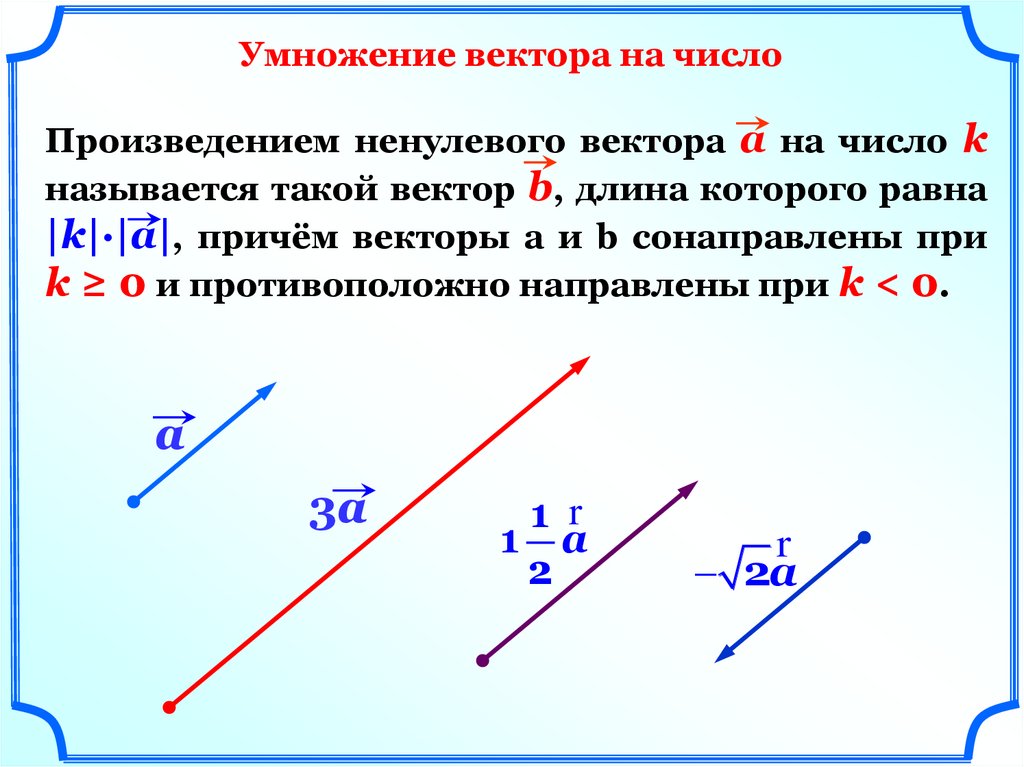
Умножение вектора на число
Произведением ненулевого вектора а на число k
называется такой вектор b, длина которого равна
|k|·|a|, причём векторы а и b сонаправлены при
k ≥ 0 и противоположно направлены при k < 0.
a
3a
1 r
1 а
2
r
2а

6.

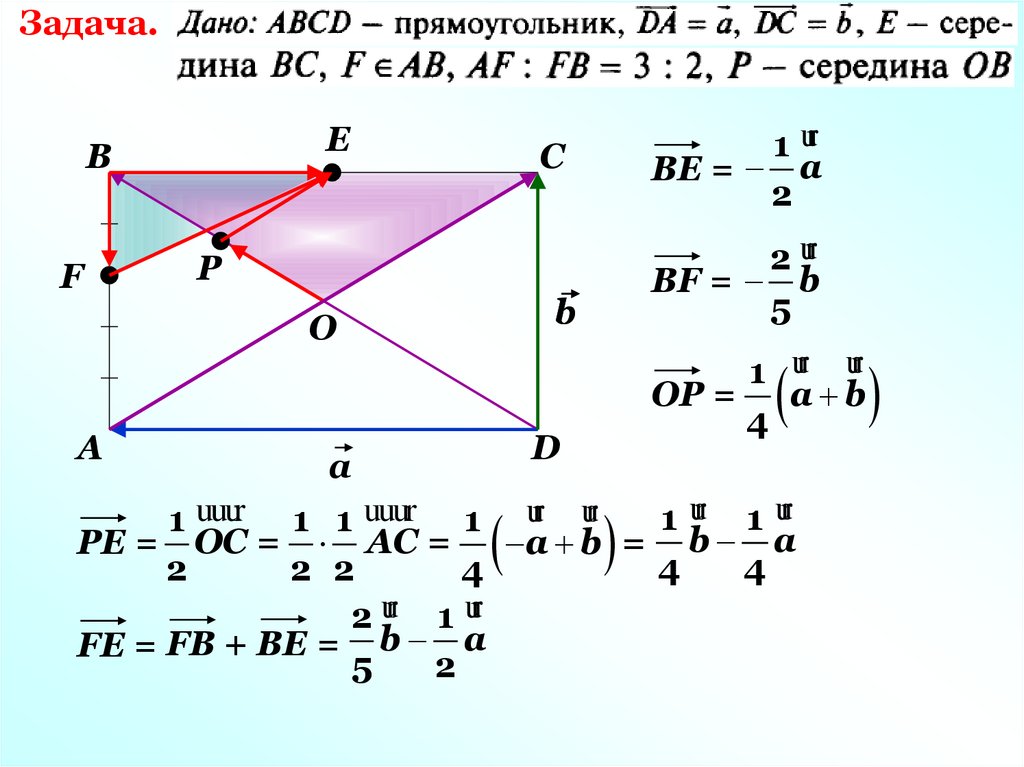
Задача.
E
B
F
C
2 ur
BF = b
5
P
b
O
A
1 ur
BE = a
2
1 ur ur
a b
OP =
4
D
a
1 ur 1 ur
1 uuur 1 1 uuur 1 ur ur
PE = OC = AC =
a b = b a
4
4
2
2 2
4
2 ur 1 ur
FE = FB + BE = b a
5
2

7.

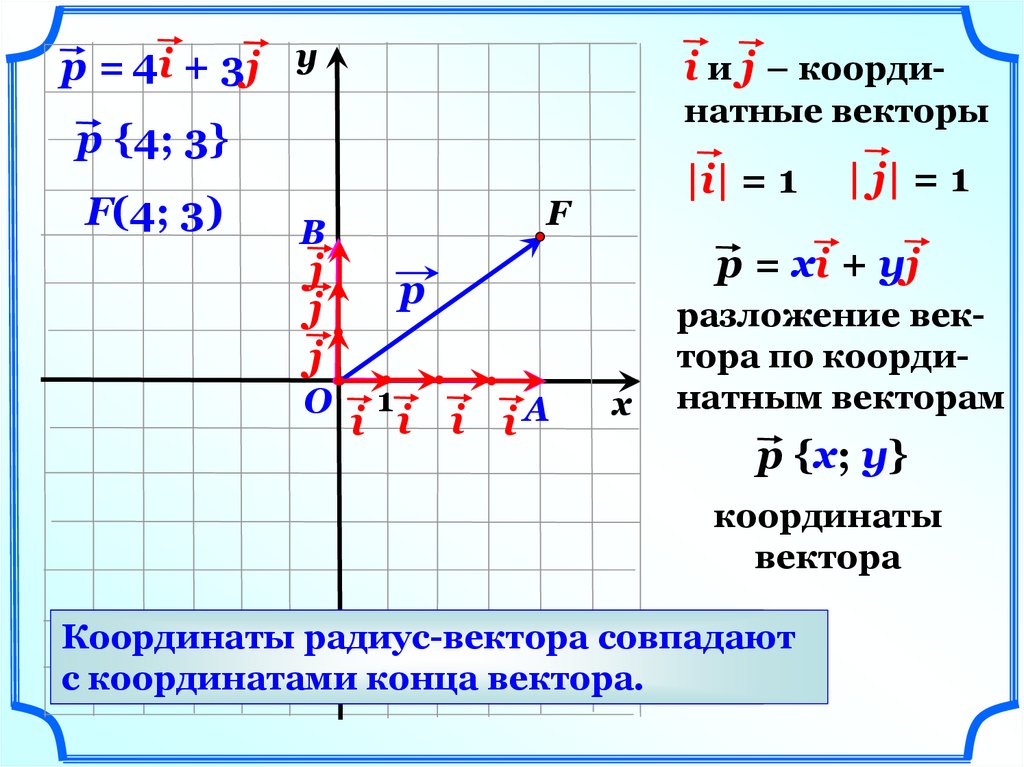
p = 4i + 3j y
i и j – координатные векторы
p {4; 3}
F(4; 3)
F
B
j
j
j
О
|i| = 1
p = xi + yj
p
1
i i i iA
| j| = 1
х
разложение вектора по координатным векторам
p {х; y}
координаты
вектора
Координаты
Вектор,
начало
радиус-вектора
которого совпадает
совпадают
с
началом
с
координатами
координат
конца
– радиус-вектор.
вектора.

8.

№ 926(в)
+
3а {– 21; – 3}
– 2b {2; – 14}
+
1
с {– 2; 3}
2
v {– 21; – 14}

9.

Признак коллинеарности двух векторов
Если координаты одного вектора пропорциональны координатам другого, то эти векторы коллинеарны.
х1 у1
=
=k
х2 у2
а{x1; у1} и b{х2; у2} – кол-
линеарны.
Если k > 0, то векторы сонаправленные.
Если k < 0, то векторы противоположно
направленные.

10.

Пример.
Коллинарны ли векторы
а{9; – 15} и b{– 3; 5}?
9
х1
=–3
=
х2 3
у1 15
=– 3
=
5
у2
k=–3
Ответ: коллинеарны, противоположно
направлены.

11.

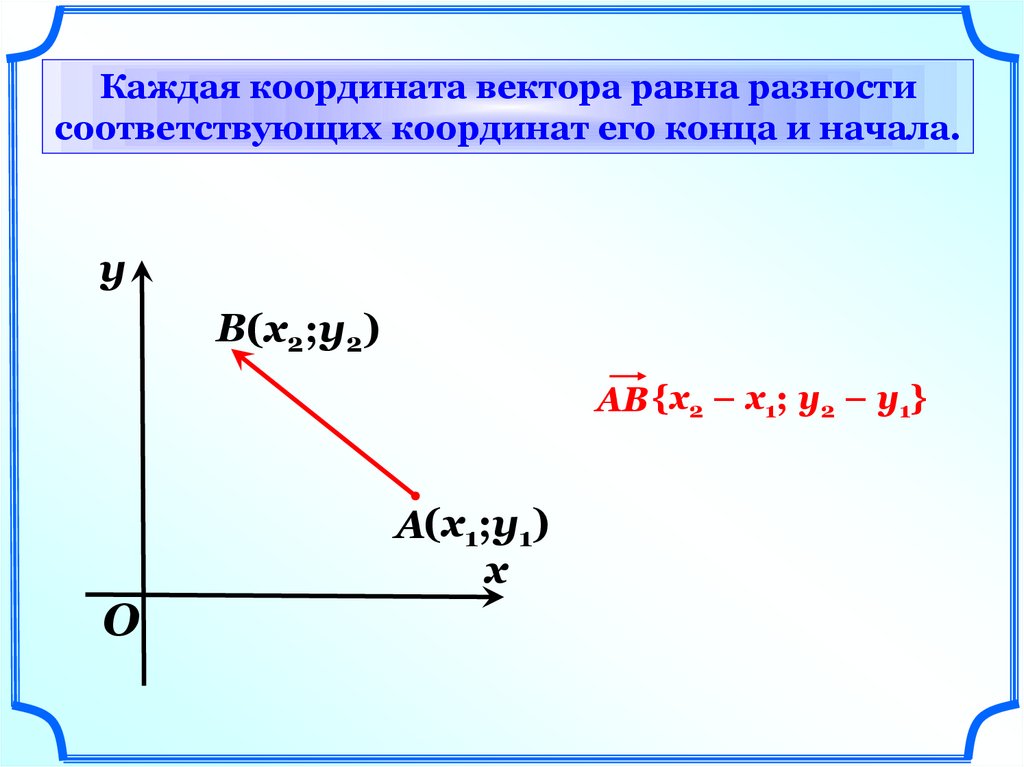
Каждая координата вектора равна разности
соответствующих координат его конца и начала.
у
B(x2;y2)
АВ {х2 – х1; у2 – y1}
A(x1;y1)
x
O

12.

№ 934(а,б)
B(x2;y2)
а) АВ {– 2 – 2; 7 – 7}
АВ {– 4; 0}
A(x1;y1)
АВ {х2 – х1; у2 – y1}
б) АВ {– 5 + 5; 27 – 1}
АВ {0; 26}

13.

Координаты середины отрезка.
Каждая координата середины отрезка равна
полусумме соответствующих координат его
концов.
у
B(x2;y2)
х1 + х2 у1 + у2
;
C
2
2
A(x1;y1)
x
O

14.

Задача.
А(– 2; 4)
Точка М – середина отрезка
ВС, значит
О(х0; у0)
С(6; 1)
М(4;
М(х1;0)
у1)
В(2; – 1)
6+2
х1 =
=4
2
1 + ( 1)
у1 =
=0
2
Точка О – середина отрезка АМ, значит
2 + 4
х0 =
=1
2
Ответ: О(1; 2).
4+0
у0 =
=2
2

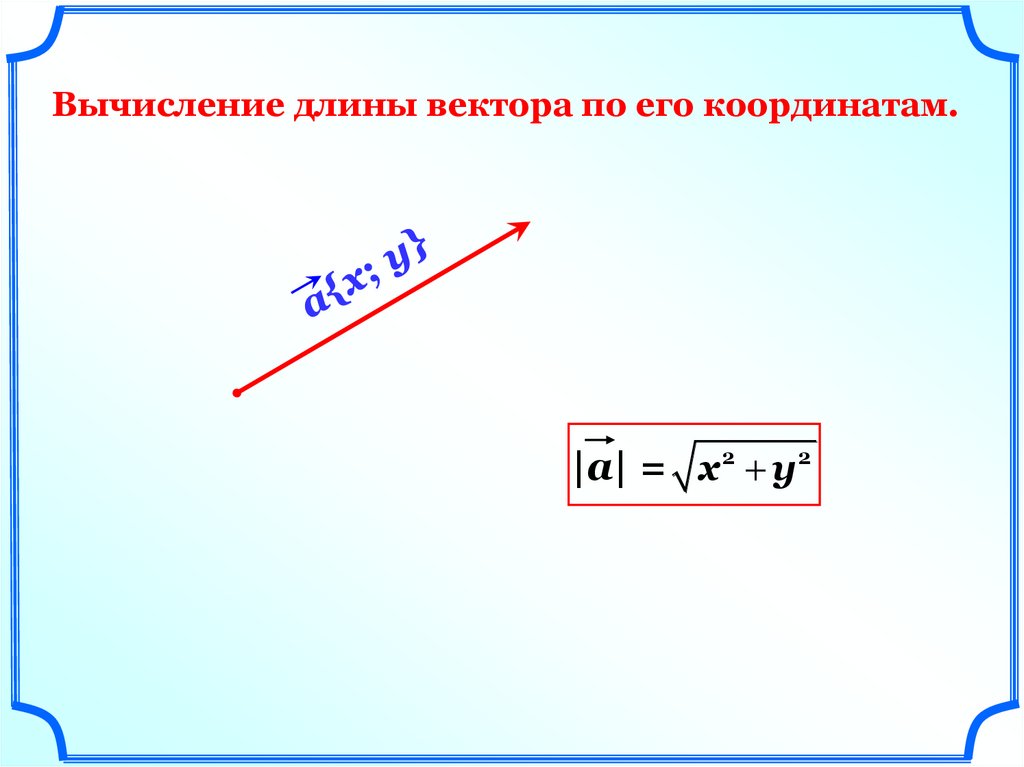
15.

Вычисление длины вектора по его координатам.
|a| = х 2 у2

16.

Задача.
AB {2 – 5; 1 – (– 3)}
AB {– 3; 4}
|AB| = ( 3)2 + 4 2 = 5
AM {5 – 5; 3 – (– 3)}
AM {0; 6}
|AM| = 02 +62 = 6

17.

Расстояние между двумя точками.
y
M2(x2;y2)
d
M1(x1;y1)
O
x
d = M1 M2 = ( х2 х1 )2 (у2 у1 )2

18.

Задача.
2 + 6 4 4
;
K
2
2
В(10; – 1)
K(2; 0)
А(– 2; 4) K(х; у) С(6; – 4)
АВ = (10+2)2 +( 1 4)2 =
122 + 52 = 13
2
2
4
+
3
=5
ВС = (10 6) +( 1+ 4) =
2
2
ВK = (10 2)2 +( 1 0)2 = 82 +12 = 65

19.

Скалярное произведение векторов
а · b = | а | · | b | · cos(а; b)
а·b=0
а ^b
а·b>0
(а; b) < 90
а·b<0
(а; b) > 90
о
а2 = |а|2
о

20.

Скалярное произведение векторов в
координатах.
Скалярное произведение векторов
а {х1; y1} и b {х2; y2}
выражается формулой
а · b = х1х2 + у1у2

21.

Косинус угла α между ненулевыми векторами
а {х1; у1} и b{х2; у2} выражается формулой:
cos α =
а·b
|а| · |b|
соs α =
х1 х2 + у1у2
х12 + у12 х22 + у22

22.

1.
а · с = 2 · 8 + 4 · (– 4) = 16 – 16 = 0
Значит, а ^ с
а · b = 2 · (– 3) + 4 · 6 = – 6 + 24 ≠ 0
Значит, а и b не перпендикулярны.

23.

1.
cos α =
b·c
|b| · |c|
=
(– 3) · 8 + 6 · (– 4)
( 3)2 +62 82 +( 4)2
=
48
48
48
8
=
=
= – 0,8 < 0
=
=
45 80 3 5 4 5 12 5 2 5
Ответ: 2) – 0,8; 3) тупой.

24.

25.

№ 1048
B(– 1; 5)
АВ{– 3; – 3}
АС{1; – 7}
C(3; 1)
А(2; 8)
cosA =
АВ · АС
|АВ| · |АС|
=
(– 3) · 1 + (– 3) · (– 7)
( 3)2 +( 3)2 12 +( 7)2
6
6
18
=
= 0,6
=
=
100 10
3 2 50
=

26.

№ 1048
B(– 1; 5)
ВА{3; 3}
ВС{4; – 4}
C(3; 1)
А(2; 8)
cosВ =
ВА · ВС
|ВА| · |ВС|
=
3 · 4 + 3 · (– 4)
32 + 32 42 +( 4)2
=0

27.

№ 1048
B(– 1; 5)
СВ{– 4; 4}
СА{– 1; 7}
C(3; 1)
А(2; 8)
cosС =
СВ · СА
|СВ| · |СА|
=
(– 4) · (– 1) + 4 · 7
( 4)2 + 4 2 ( 1)2 +7 2
8
8
32
= 0,8
=
=
=
100 10
4 2 50
=

28.

№ 1050
Скалярный квадрат вектора равен квадрату его
длины.
а2 = |а|2
|а + b|2 = (a + b)2 = a2 + 2ab + b2 =
= 52 + 2 · 5 · 8 · cоs60о + 82 =
1
= 25+2 40 +64 = 129
2
|а + b| = 129
|а – b| = 7

29.

№ 1052
р · q = (a – b – с) · (а – b + с) =
= a2 – аb + ас – аb + b2 – bс – ас + bс – c2 =
0
= a2 – 2ab + b2 – c2 = 25 – 16 + 4 = 13

30.

№ 1053
а · b = (3р – 2q) · (р + 4q) =
= 3р2 + 12рq – 2рq – 8q2 = 3 – 8 = – 5

31.

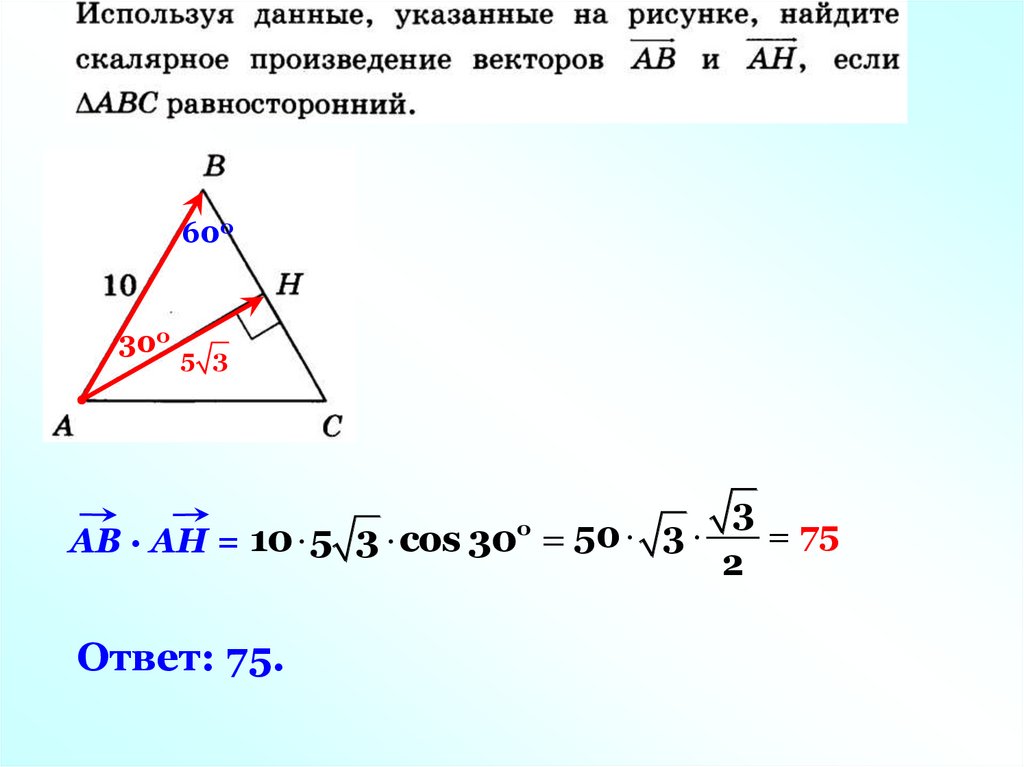
600
300
5 3
3
75
АВ · АН = 10 5 3 соs 30 50 3
2
о
Ответ: 75.