Функции. Подготовка к контрольной работе. Урок 26

1.

17.10.2023
К л а с с н а я р а б о т а.
Подготовка к контрольной
работе.

2.

План исследования функции
1. Область определения
2. Область значений
3. Нули функции
4. Промежутки знакопостоянства
5. Промежутки монотонности
6. Наибольшее и наименьшее значения
7. Чётность функции
8. Асимптоты

3.

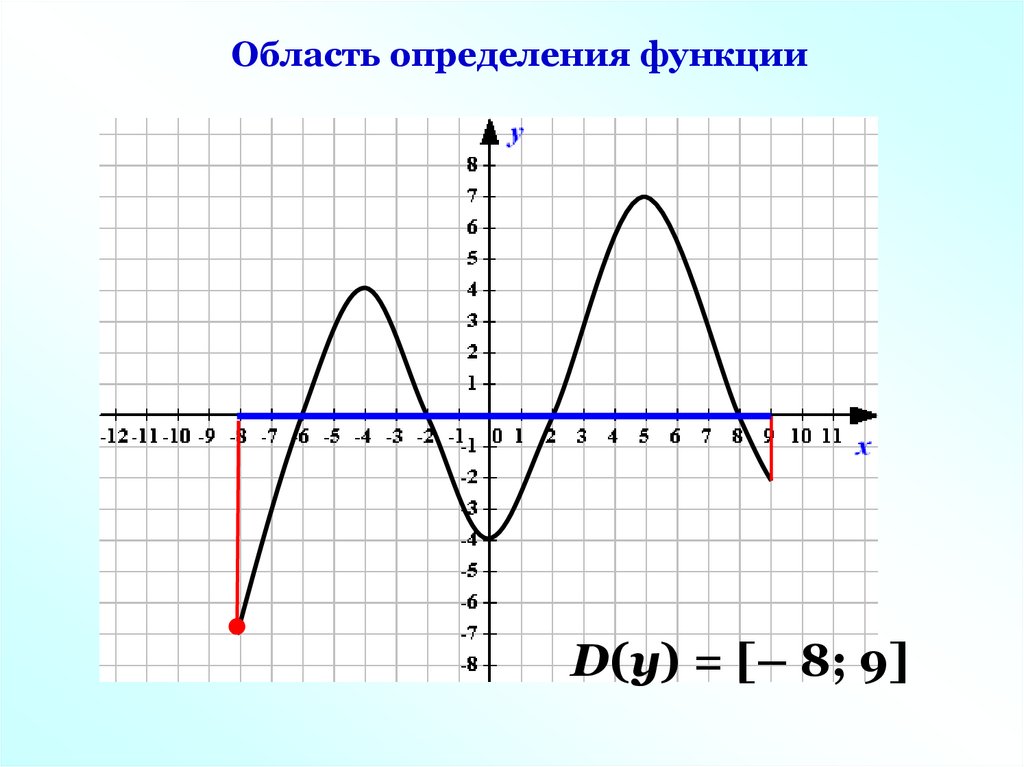
D(у) – все значения независимой
переменной (х).

4.

Область определения функции
D(у) = [– 8; 9]

5.

Для нахождения области определения
функции заданной формулой необходимо
проверить
выполнение
следующих
условий:
1)
знаменатели дробей, входящих
формулу, не должны равняться нулю;
в
2) если формула содержит квадратные корни, то подкоренные выражения должны
быть неотрицательны (≥ 0).

6.

№1
Найдите область определения функции:
х +2
у=
2 3х + х2
х+2≥0
х2 – 3х + 2 ≠ 0
х+2≥0
х2 – 3х + 2 ≠ 0
х ≥–2
х1 ≠ 2
х2 ≠ 1
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
-2
1
2
D(у) = [ – 2; 1), (1; 2), (2; +∞).
x

7.

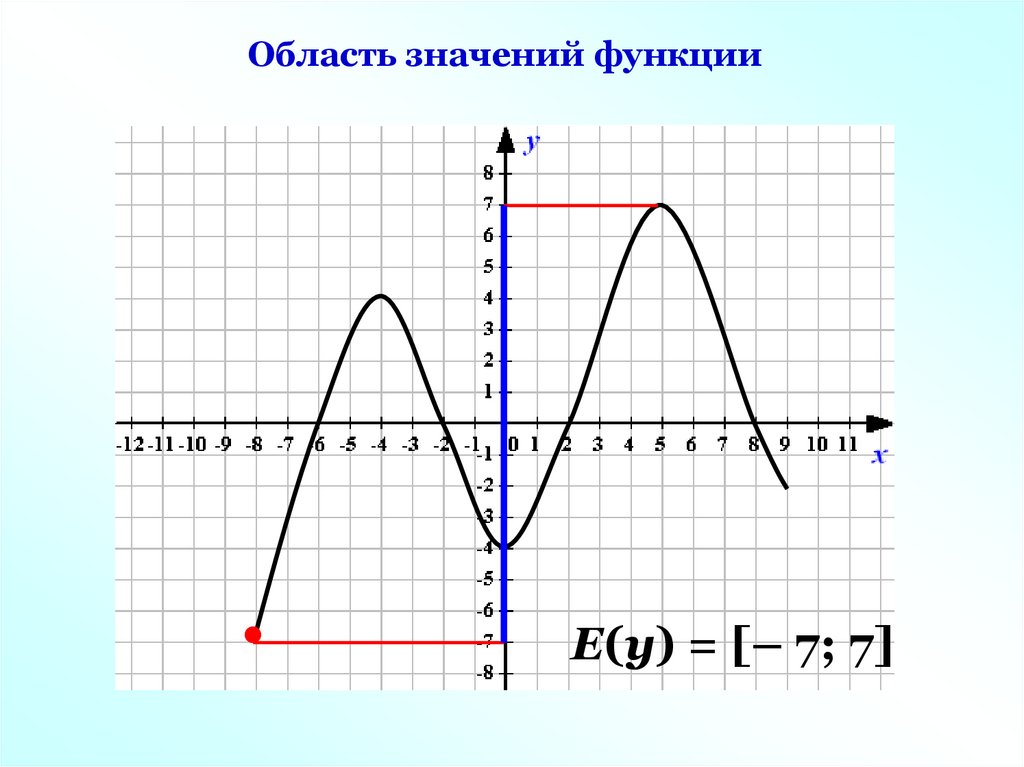
Область значений функции
Е(у) = [– 7; 7]

8.

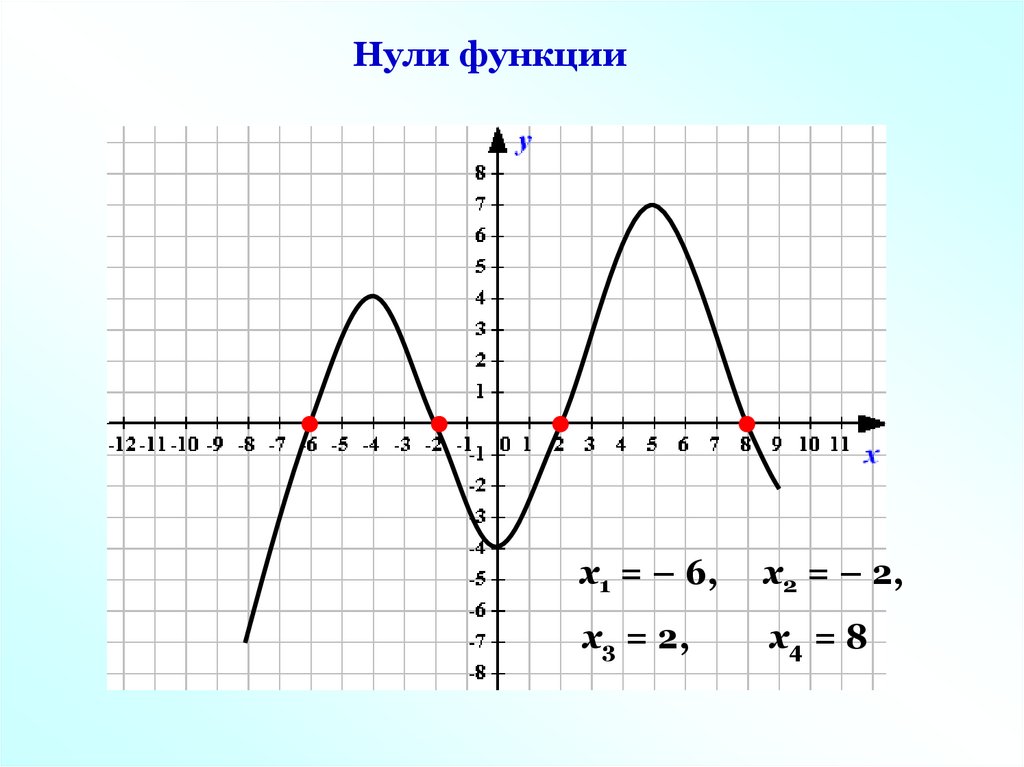
Нули функции
х1 = – 6,
х2 = – 2,
х3 = 2,
х4 = 8

9.

№ 2 Найдите нули функции: у = 12х2 + 2х – 10.
12х2 + 2х – 10 = 0
6х2 + х – 5 = 0
у2 + у – 5 · 6 = 0
у1 = 5
у2 = – 6
5
х1 =
6
х2 = – 1
5
Ответ: х1 =
6
х2 = – 1.

10.

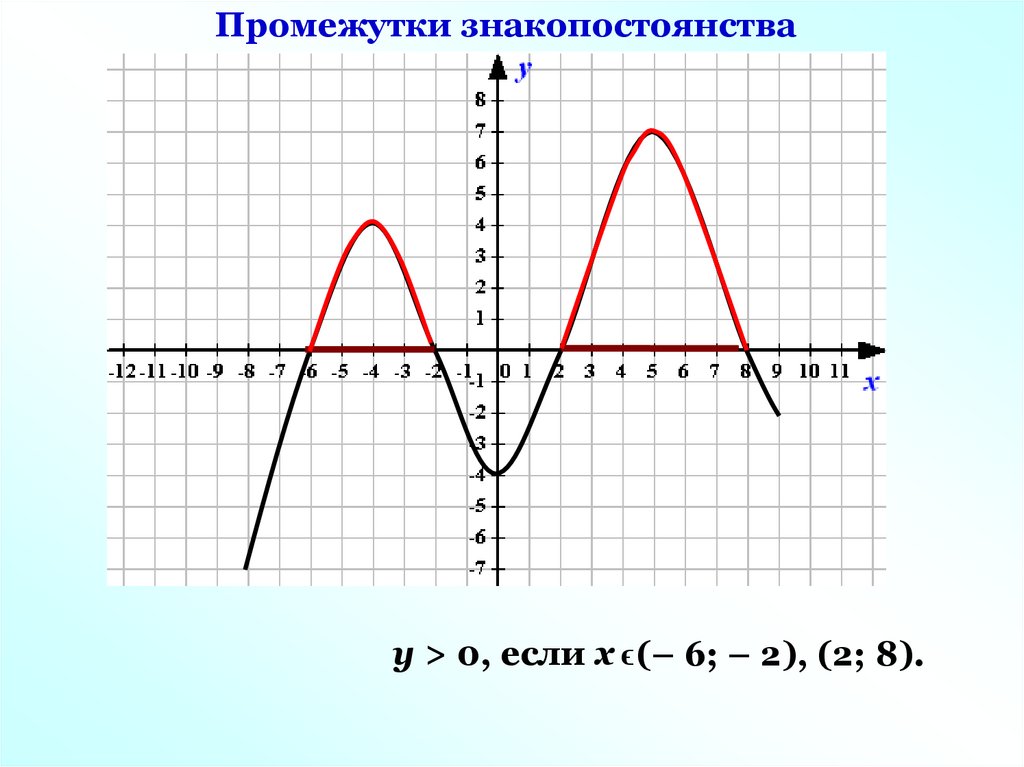
Промежутки знакопостоянства
у > 0, если х ϵ (– 6; – 2), (2; 8).

11.

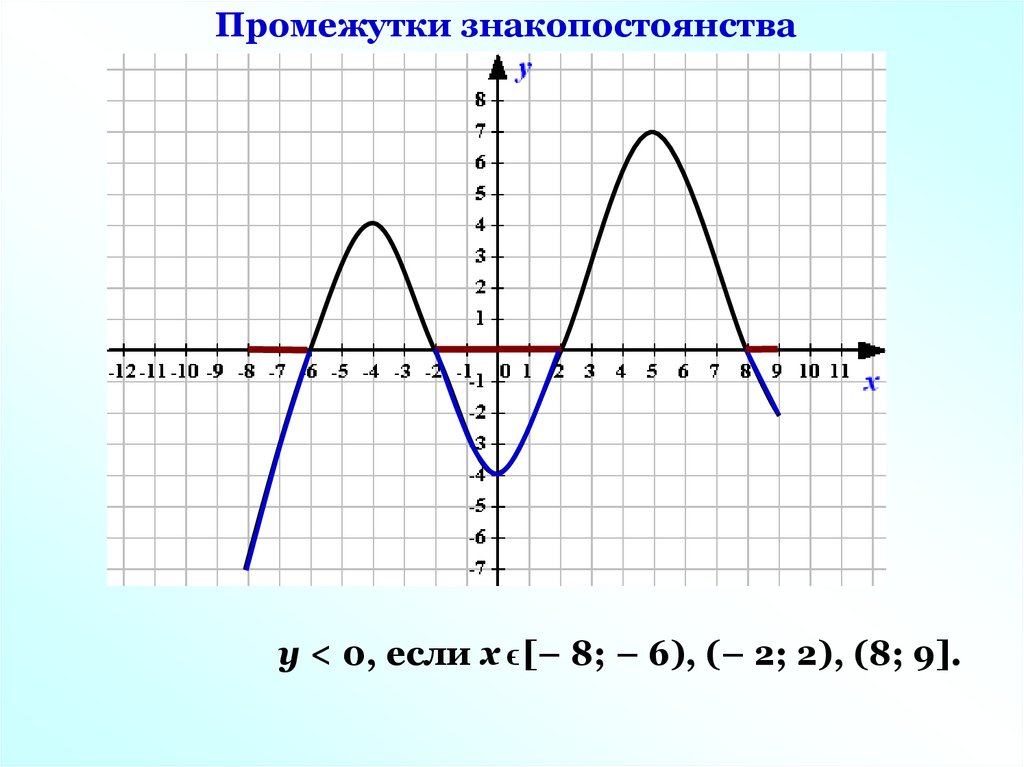
Промежутки знакопостоянства
у < 0, если х ϵ [– 8; – 6), (– 2; 2), (8; 9].

12.

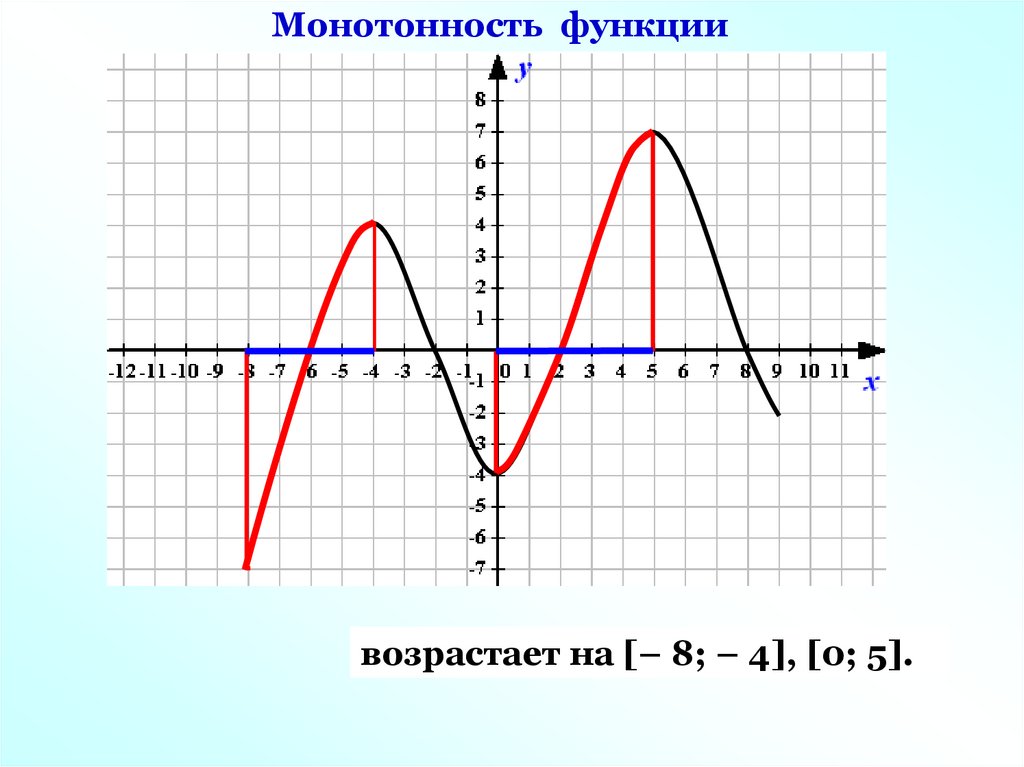
Монотонность функции
возрастает на [– 8; – 4], [0; 5].

13.

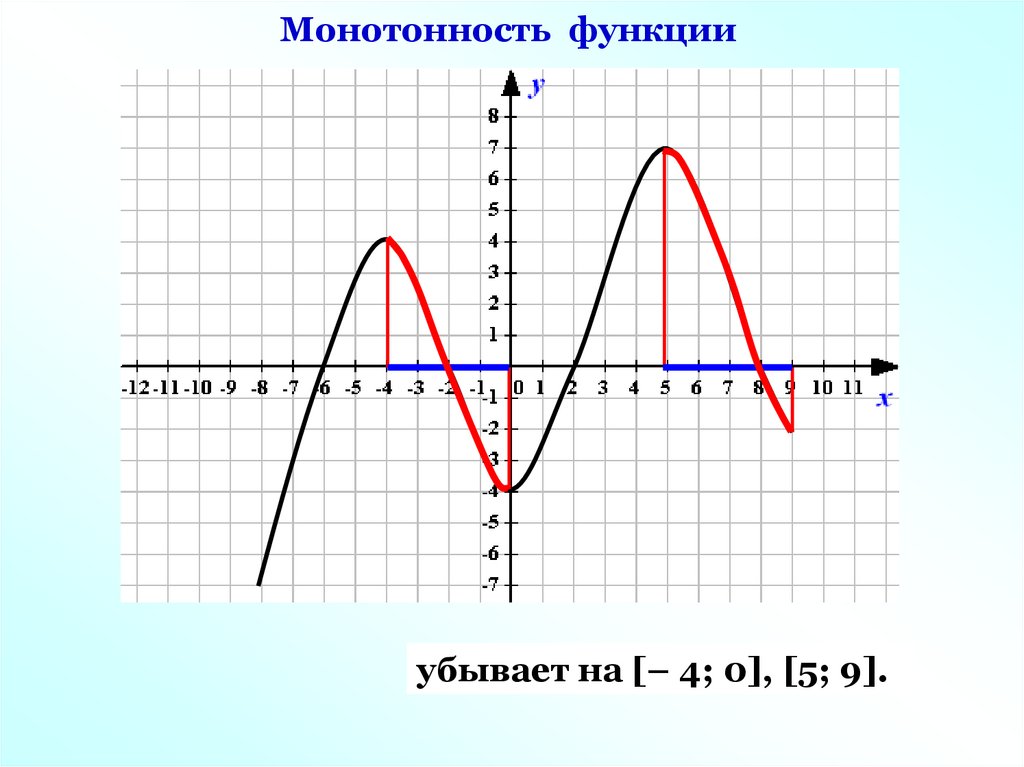
Монотонность функции
убывает на [– 4; 0], [5; 9].

14.

y
y2
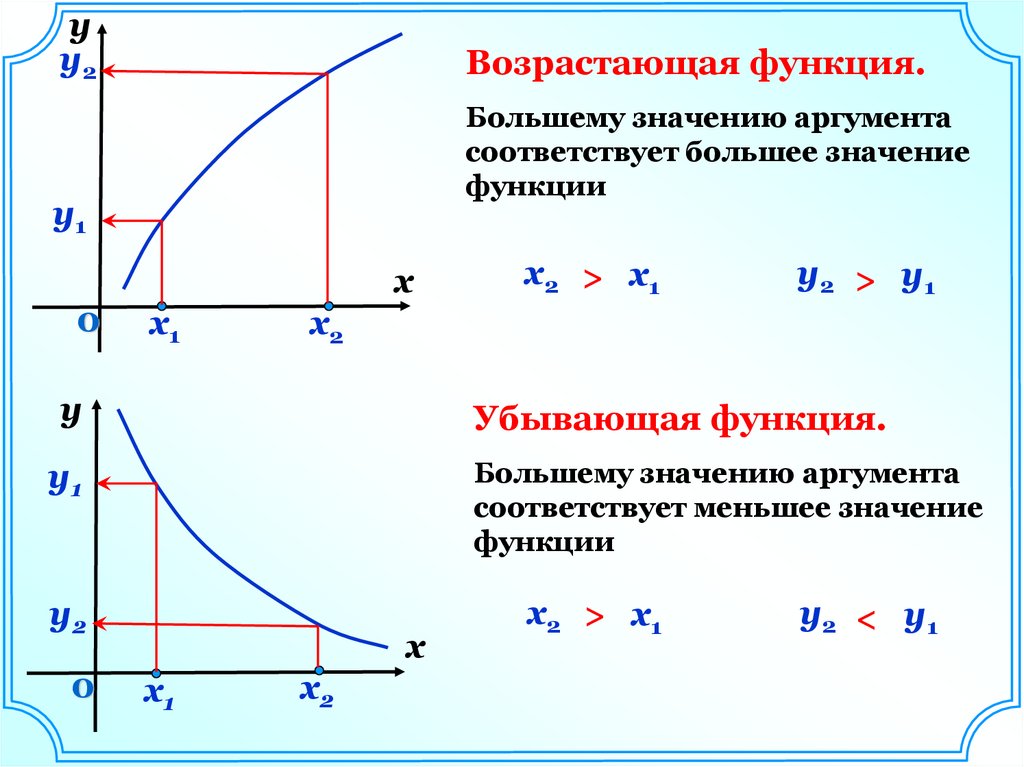
Возрастающая функция.
Большему значению аргумента
соответствует большее значение
функции
y1
0
x
x1
x2 > x1
y2 > y1
x2
y
Убывающая функция.
y1
Большему значению аргумента
соответствует меньшее значение
функции
y2
0
x
x1
x2
x2 > x 1
y2 < y 1

15.

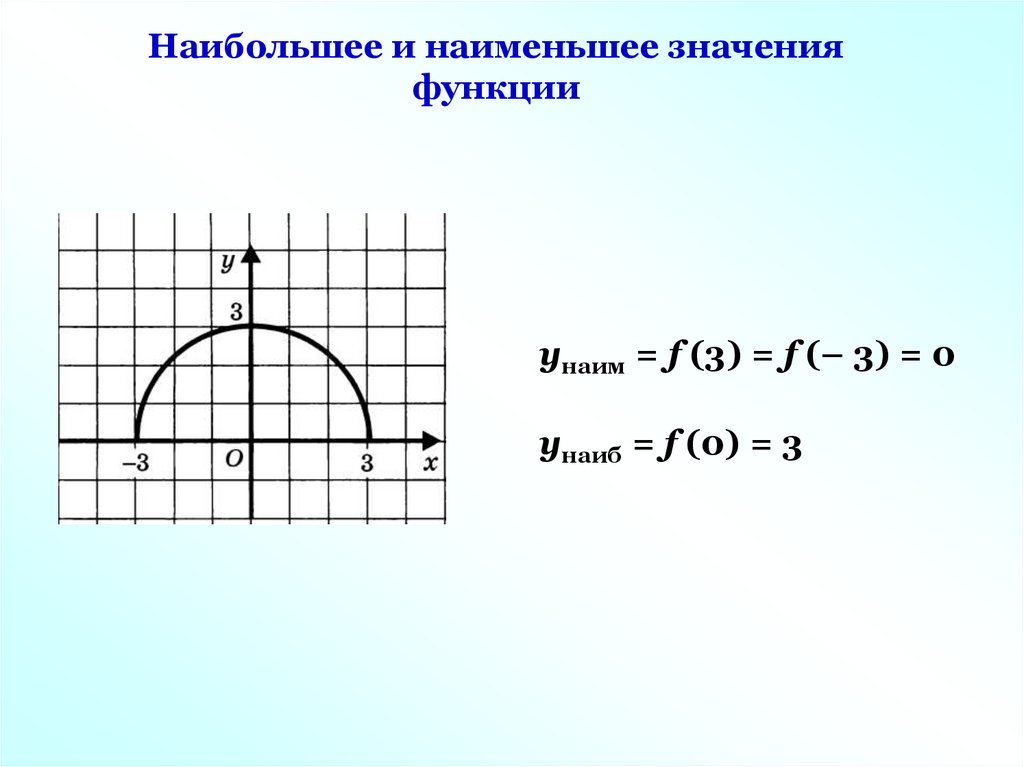
Наибольшее и наименьшее значения
функции
унаим = f (3) = f (– 3) = 0
унаиб = f (0) = 3

16.

Чётная функция
1) Область определения симметрична
относительно 0.
2) f(– х) = f(х), для любых х ϵ D(f).
Пример. у = 2х4 – х2
1) D(f) = (– ∞; + ∞)
2) f(– х) = 2·(– х)4 – (– х)2 = 2х4 – х2 = f(х)
Ф-ция у = 2х4 – х2 чётная.

17.

Нечётная функция
1) Область определения симметрична
относительно 0.
2) f(– х) = – f(х), для любых х ϵ D(f).
Пример. у = 3х5 – х3
1) D(f) = (– ∞; + ∞)
2) f(– х) = 3·(– х)5 – (– х)3 = – 3х5 + х3 =
= – (3х5 – х3) = – f(х)
Ф-ция у = 3х5 – х3 нечётная.

18.

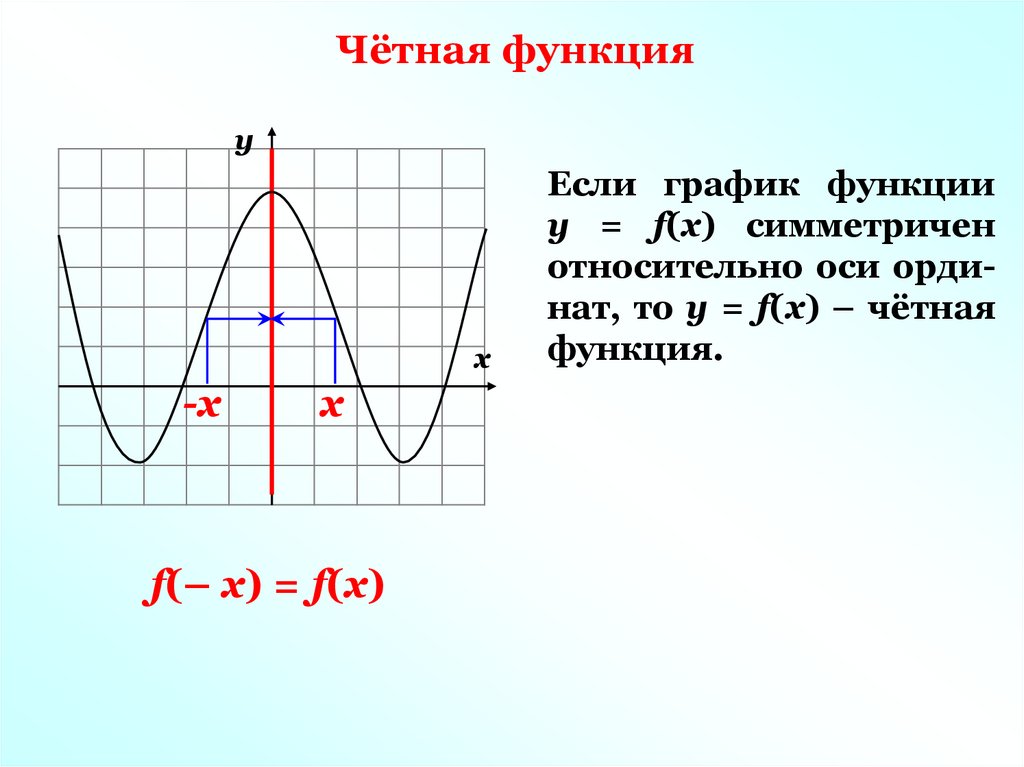
Чётная функция
у
х
-x
x
f(– х) = f(х)
Если график функции
у = f(х) симметричен
относительно оси ординат, то у = f(х) – чётная
функция.

19.

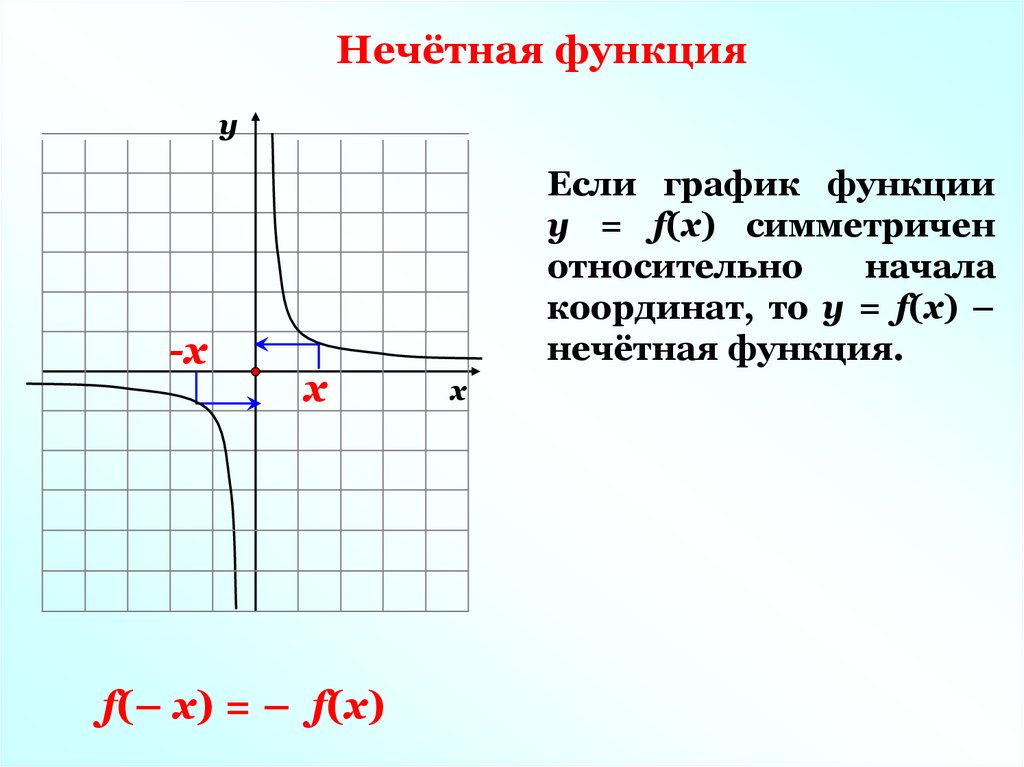
Нечётная функция
у
-x
x
f(– х) = – f(х)
Если график функции
у = f(х) симметричен
относительно
начала
координат, то у = f(х) –
нечётная функция.
х

20.

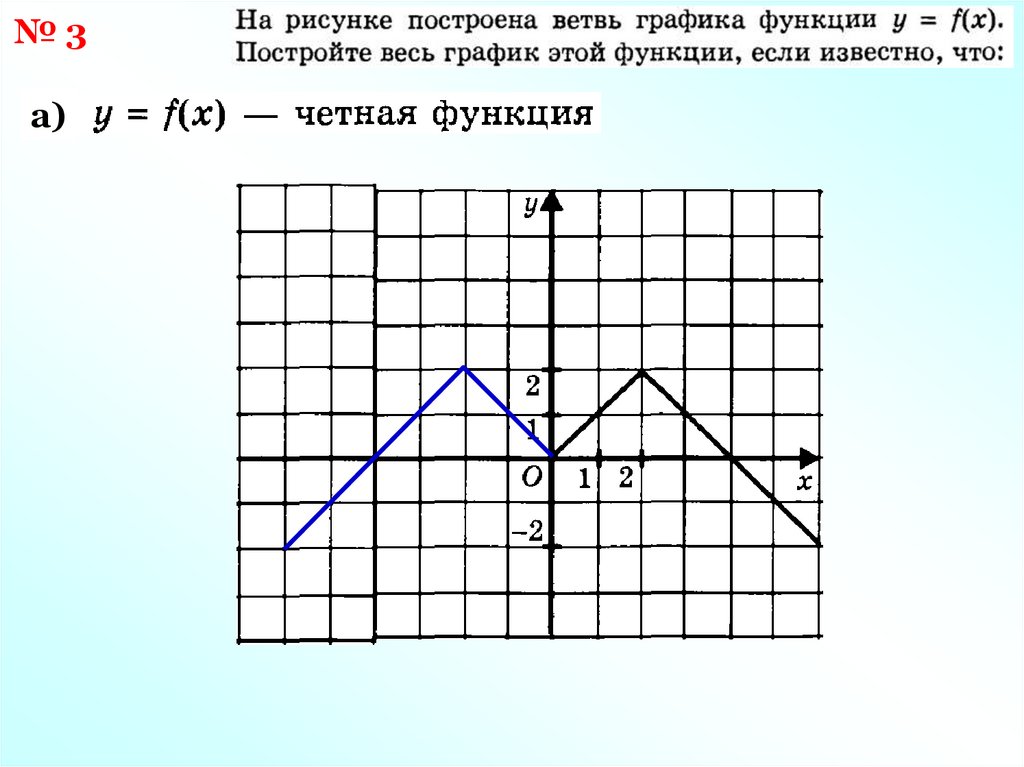
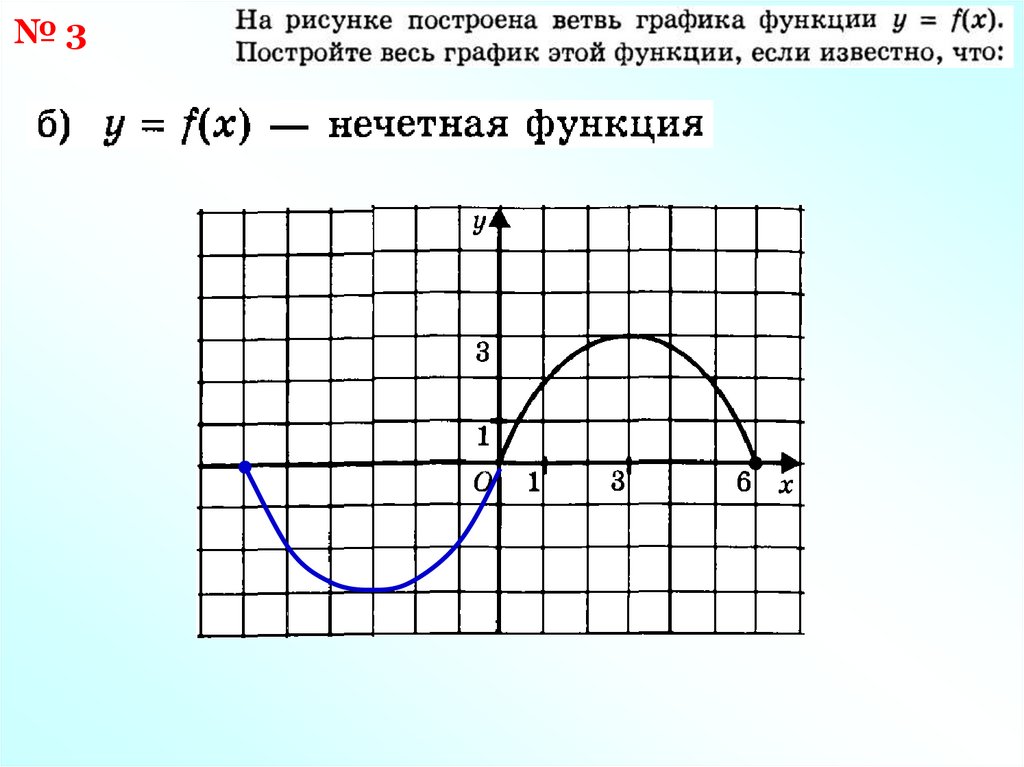
№3
а)

21.

№3

22.

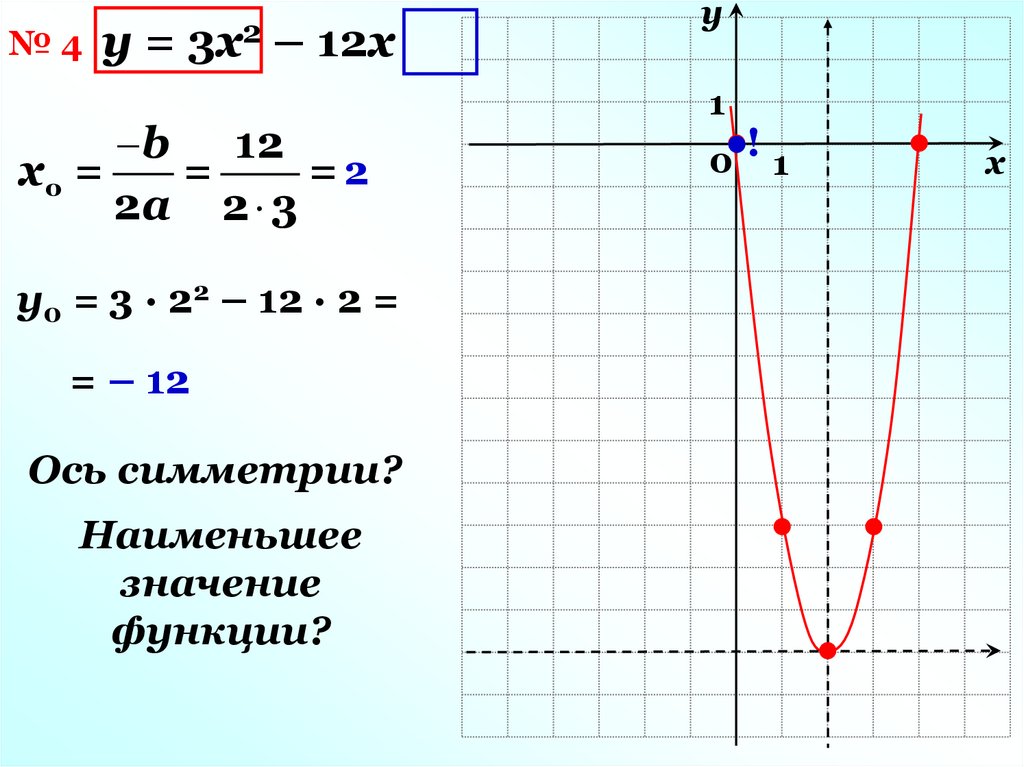
№ 4 y = 3x2 – 12x
b
12
хо =
=
=2
2a 2 3
у0 = 3 · 22 – 12 · 2 =
= – 12
Ось симметрии?
Наименьшее
значение
функции?
у
1
0!1
х

23.

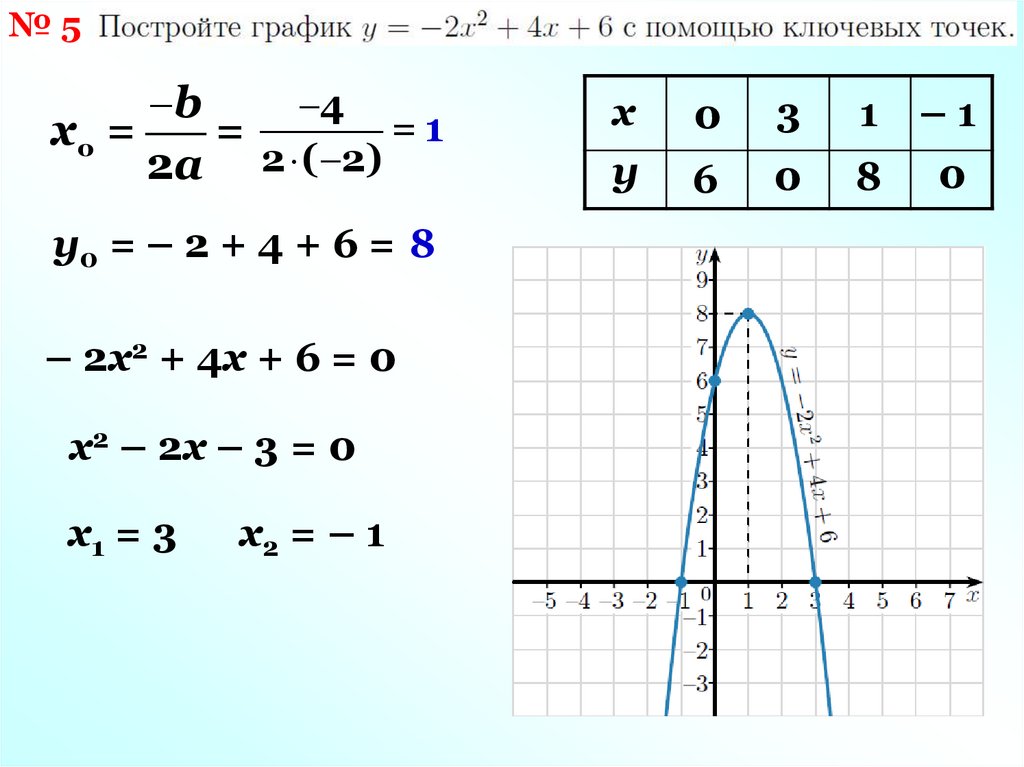
№5
b
4
=1
хо =
=
2a 2 ( 2)
у0 = – 2 + 4 + 6 = 8
– 2х2 + 4х + 6 = 0
х2 – 2х – 3 = 0
х1 = 3
х2 = – 1
х
у
0
3
1
–1
6
0
8
0

24.

Подготовиться к
контрольной работе