Случайная величина и распределение вероятностей

1.

«Случайные величины. Закон
распределения случайной
величины»

2.

Случайная величина
Случайной называется величина, которая в
результате испытания может принять то или иное
числовое значение, причем заранее неизвестно, какое
именно.
Случайная величина связана со
случайным событием.
Если случайное событие качественная
характеристика
испытаний, то случайная величина
его
количественная
характеристика.

3.

Случайная величина
Если для какой-либо величины ее измерение
повторять многократно в практически одинаковых
условиях, то обнаружится, что всякий раз получаются
несколько отличные друг от друга результаты.
Таким образом, возможные значения случайных
величин принадлежат некоторым числовым множествам.
Случайным является то, что на этих множествах
величины могут принять любое значение, но какое
именно, заранее сказать нельзя.

4.

Случайная величина
Случайные
величины
латинскими буквами
обозначают
заглавными
X ,Y , Z ,
а их возможное значение – прописными буквами
xi , y i , z i
При
многократных
испытаниях
определенные
значения случайной величины могут встречаться
несколько раз, поэтому для задания случайной величины
недостаточно перечислить все её возможные значения.

5.

Случайная величина
Так же необходимо знать, как часто могут появляться
те или иные значения в результате испытания при одних
и тех же условиях, т.е. нужно задать вероятности их
появления.
Вероятность того, что случайная величина примет
определенное значение обозначают:
P( X x1 ) p1
и т.д.

6.

Виды случайных величин
1
2
• Дискретные величины
• Непрерывные величины
1

7.

Дискретные случайные величины
Дискретные – такие случайные величины, которые
принимают счетное множество значений, т.е. такое
множество, элементы которого можно подсчитать.
значения чисел на
верхней грани
брошенной игральной
кости

8.

Дискретные случайные величины
Так же примерами дискретных случайных величин
могут служить
Число при
попаданий в
мишень
Число вызовов за
сутки

9.

Непрерывные случайные величины
Непрерывные – такие случайные величины, которые
могут принимать любые значения, но в определенном
интервале. Занумеровать все значения такой величины
просто невозможно, поэтому они образуют несчетное
множество.
чаще всего к ним
относятся значения
некоторых
физических величин

10.

Непрерывные случайные величины
Так же примерами непрерывных случайных величин
могут служить
Рост детей
Расстояние, которое
пролетит ядро

11.

Закон распределения
Закон распределения случайной величины - это
соответствие,
установленное
между возможными
значениями случайной величины и их вероятностями.
Законы распределения могут быть заданы тремя
способами: табличным, графическим, аналитическим.
Способ задания зависит от типа случайной величины.

12.

Закон распределения
Простейшим способом задания закона распределения
является табличный способ.
Табличную форму задания называют также рядом
распределения.
n
При этом pi 1 , где суммирование распространяется
i 1
на все (конечное или бесконечное) множество
возможных значений данной случайной величины .

13.

Решение задач
№ 1. Даны вероятности значений случайной величины
: значение 10 имеет вероятность 0,3; значение 2 –
вероятность 0,4; значение 8 – вероятность 0,1; значение 4
– вероятность 0,2. Построить ряд распределения
случайной величины .
Решение: расположив значения случайной величины в
возрастающем порядке, получим ряд распределения:

14.

Решение задач
Возьмем на плоскости хОр точки (2; 0,4), (4; 0,2), (8;
0,1) и (10; 0,3). Соединив последовательные точки
прямолинейными отрезками, получим многоугольник
(или полигон) распределения случайной величины
p
0,4
Многоугольником распределения вер
оятностей данной величины называют
ломаную, звенья которой соединяют
соседние
точки.
Иногда
вместо
«многоугольника» используют термин
полигон, но этот вариант больше в ходу в
математической статистике
0,3
0,2
0,1
0
2
4
6
8
10
x

15.

Решение задач
№ 2. Разыгрываются две вещи стоимостью по 5000 руб
и одна вещь стоимостью 30000 руб. Составить закон
распределения выигрышей для человека, купившего
один билет из 50.
Решение:
Искомая случайная величина представляет собой
выигрыш и может принимать три значения: 0, 5000 и
30000 руб. Первому результату благоприятствует 47
случаев, второму результату - два случая и третьему –
один случай. Найдем их вероятности:
P( x1 )
47
0,94
50
P( x2 )
2
0,04
50
P ( x3 )
1
0,02
50

16.

Решение задач
Закон распределения случайной величины имеет вид:
В качестве проверки найдем
P( x1 ) P( x2 ) P( x3 ) 0,94 0,04 0,02 1

17.

№ 4. Задай с помощью таблицы распределение
вероятностей случайной величины X, равной числу
орлов, выпавших при двух бросках монеты.
Значение
Вероятность
0
1
2

18.

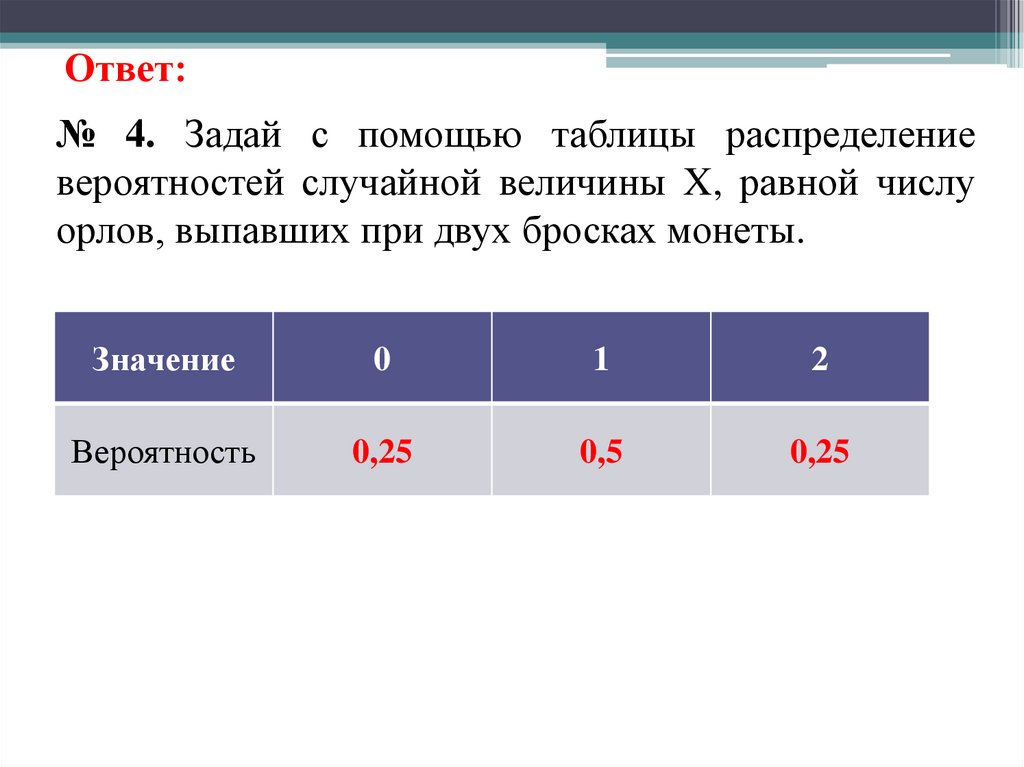
Ответ:
№ 4. Задай с помощью таблицы распределение
вероятностей случайной величины X, равной числу
орлов, выпавших при двух бросках монеты.
Значение
0
1
2
Вероятность
0,25
0,5
0,25

19.

№ 5. В таблице дано распределение вероятностей
некоторой
случайной
величины.
Одна
из
вероятностей неизвестна. Найди её.
Решение:
Напоминаю основное свойство распределения: сумма всех
вероятностей равна единице.
Исходя из этого, мы от единицы должны отнять сумму всех
вероятностей, то есть 1 – (0,12 + 0,24 + 0,13 + 0,27) = 0,24.
Ответ: 0,24.

20.

№ 6. Распределение вероятностей
величины Х задано таблицей.
случайной
Значение Х
0
0,5
1
1,5
2
Вероятность
0,15
0,11
0,08
0,5
0,25
Найдите вероятность события «Х < 1,5»
Решение:
1) Выбираем значения Х, которые меньше 1,5. Получается,
что у нас остаётся три значения: 0, 0,5 и 1.
2) 0,15 + 0,11 + 0,08 = 0,34.
Ответ: 0,34.

21.

Домашнее задание
№1. В таблице построено распределение случайной
величины «сумма очков при бросании двух
игральных костей». Заполните недостающие
ячейки (ответы запишите в виде десятичной
дроби).

22.

№2. В таблице дано распределение вероятностей
некоторой
случайной
величины.
Одна
из
вероятностей неизвестна. Найди её.

23.

№3. Распределение вероятностей случайной
величины Х задано таблицей.
Значение Х
0
0,5
1
1,5
2
Вероятность
0,05
0,24
0,1
0,15
0,46
Найдите вероятность события «Х > 1»