Similar presentations:
Моменты импульса (угловые моменты). Часть вторая
1.
Русакова Н.П.Квантовая механика и квантовая химия
Лекция № 7
Моменты импульса
(угловые моменты)
Часть вторая
3 курс ХТФ
2.
Русакова Н.П.Квантовая механика и квантовая химия
Часть 2
Моменты импульса
Лекция № 7
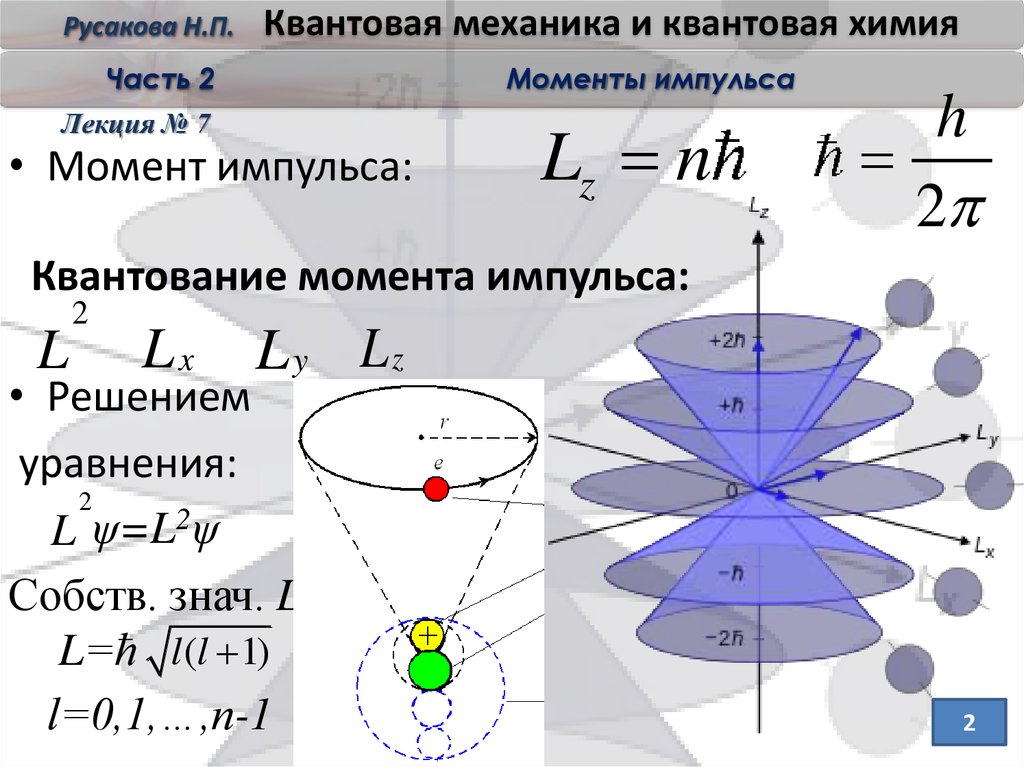
• Момент импульса:
Lz n
h
2
Квантование момента импульса:
L
2
Lx
Ly Lz
• Решением
уравнения:
2
L ψ=L2ψ
Собств. знач. L
L=ћ l (l 1)
l=0,1,…,n-1
2
3.
Русакова Н.П.Квантовая механика и квантовая химия
Часть 2
Моменты импульса
Лекция № 7
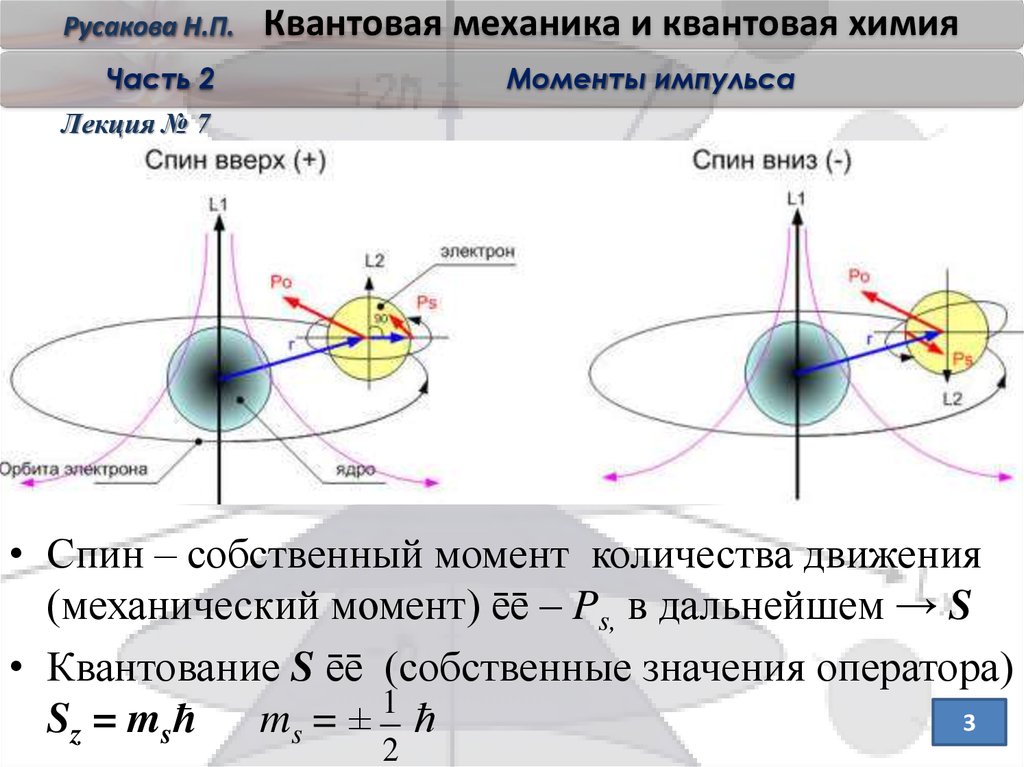
• Спин – собственный момент количества движения
(механический момент) ēē – Ps, в дальнейшем → S
• Квантование S ēē (собственные значения оператора)
3
Sz = msћ
ms = ± 1 ћ
2
4.
Русакова Н.П.Квантовая механика и квантовая химия
Часть 2
Моменты импульса
Лекция № 7
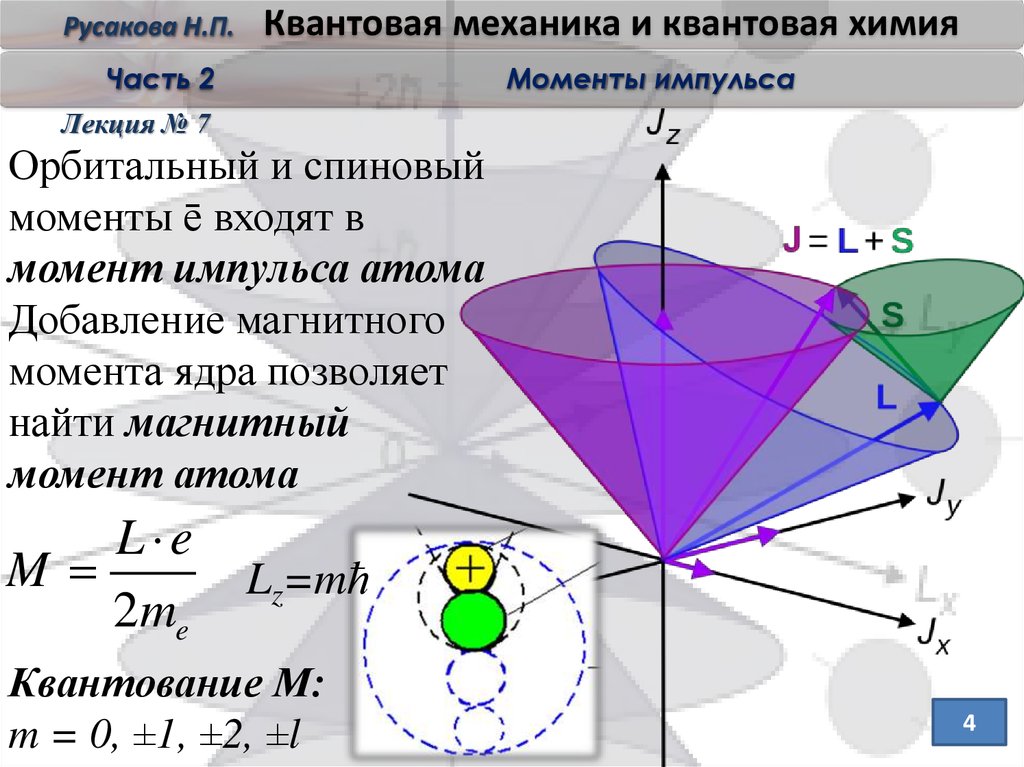
Орбитальный и спиновый
моменты ē входят в
момент импульса атома
Добавление магнитного
момента ядра позволяет
найти магнитный
момент атома
L e
M
2me
Lz=mћ
Квантование М:
m = 0, ±1, ±2, ±l
4
5.
Русакова Н.П.Часть 2
Квантовая механика и квантовая химия
Моменты импульса
Лекция № 7
Полный момент импульса молекулы. Зачем??
Основная характеристика молекулы – полная энергия:
Ĥψ = Еψ
Е = T + U = Tt + Tr + Tv + Uen + Unn + Uee
внешние силы
внутренние силы
1
T = Tt + Tr + Tv T = mi v 2 0,i
2 i
Классич. мех.:
p mv
Мера мех. движения тела
5
6.
Русакова Н.П.Квантовая механика и квантовая химия
Часть 2
Моменты импульса
Лекция № 7
Полный импульс системы материальных точек:
p mi vi
i
2
Одновременное значение могут иметь: L и одна из
проекций оператора импульса на оси. Две остальные
остаются неопределёнными. Поэтому вектор момента
импульса не имеет определённого направления и не
может быть изображён (как в классической мех.).
Инерция I
-Это явление сохранения покоя или сохранения скорости прямолинейного равномерного движения при
компенсации (или отсутствии) внешних воздействий
2
Для расчёта I вводят инерциальную
систему отсчёта 6
I mr
7.
Русакова Н.П.Часть 2
Квантовая механика и квантовая химия
Моменты импульса
Лекция № 7
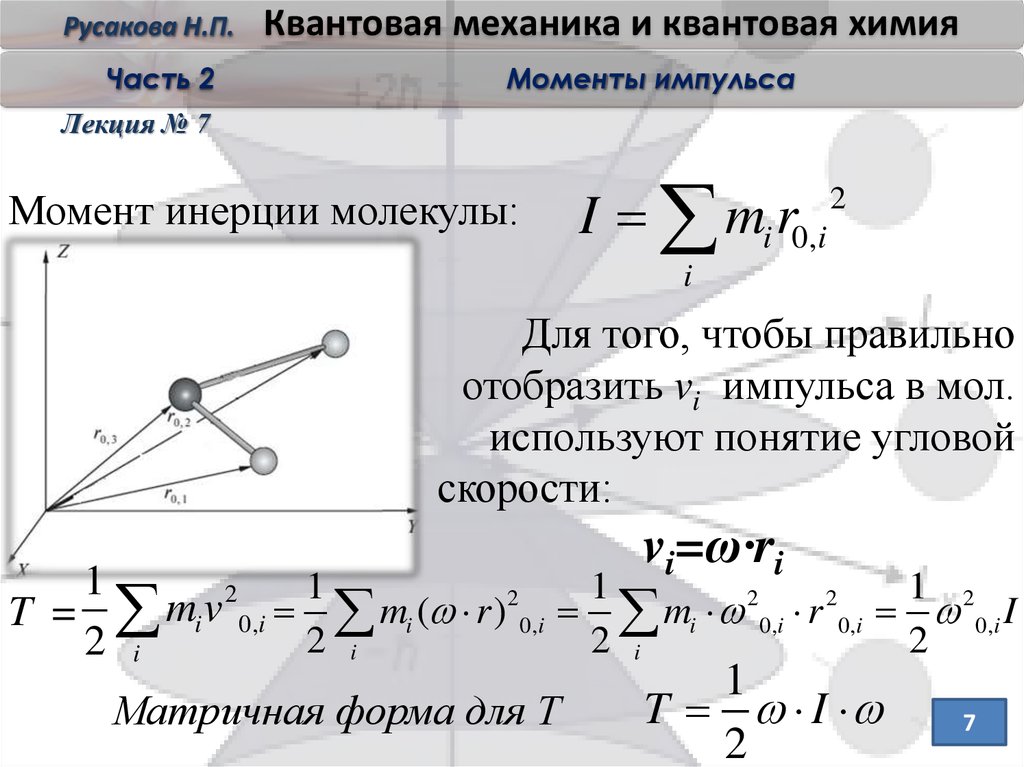
Момент инерции молекулы:
I mi r0,i
2
i
Для того, чтобы правильно
отобразить vi импульса в мол.
используют понятие угловой
скорости:
vi=ω·ri
1
1
1
1 2
2
2
2
2
T = mi v 0,i mi ( r ) 0,i mi 0,i r 0,i 0,i I
2 i
2 i
2
2 i
Матричная форма для Т
1
T I
2
7
8.
Русакова Н.П.Квантовая механика и квантовая химия
Часть 2
Моменты импульса
Лекция № 7
В системе центра масс угловая скорость и
момент инерции записываются в виде матриц:
-ω задается ко- и контрвариантным способом
-I – тензором второго ранга
1
T I
2
1
x
2
y
I xx
z I
yx
I zx
I xy
I yy
I zy
I xz
I yz
I zz
x
y
z
8
9.
Квантовая механика и квантовая химияРусакова Н.П.
Часть 2
Моменты импульса
Лекция № 7
• Матрица тензора момента
инерции состоит из компонент
центробежных моментов I=
Она является матрицей интегралов по элементу массы:
I xx ( y z )dm
2
2
I yy ( x z )dm
2
2
I zz ( x y )dm
2
2
I xx
I
yx
I zx
I xy
I yy
I zy
I xz
I yz
I zz
I xy I yx ( xy )dm
I yz I zy ( yz )dm
I xz I zx ( zx)dm
9
10.
Русакова Н.П.Часть 2
Квантовая механика и квантовая химия
Моменты импульса
Лекция № 7
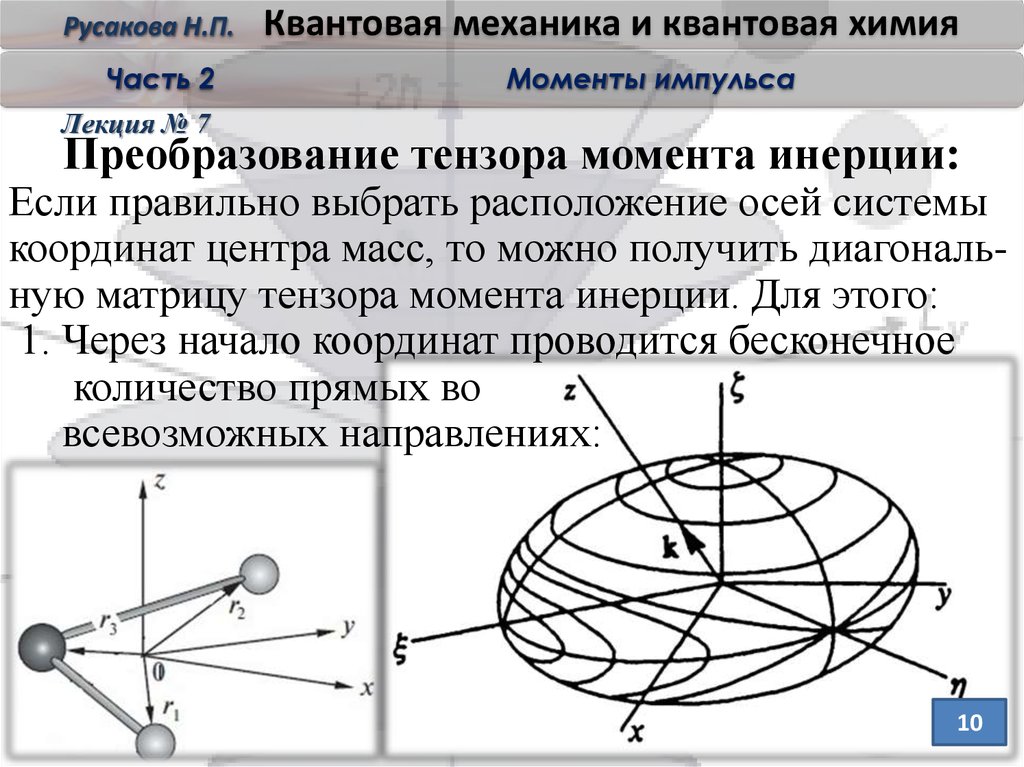
Преобразование тензора момента инерции:
Если правильно выбрать расположение осей системы
координат центра масс, то можно получить диагональную матрицу тензора момента инерции. Для этого:
1. Через начало координат проводится бесконечное
количество прямых во
всевозможных направлениях:
10
11.
Русакова Н.П.Часть 2
Квантовая механика и квантовая химия
Моменты импульса
Лекция № 7
Преобразование тензора момента инерции:
1
2. На прямых откладываются отрезки длиной r
3. Из них получается поверхность
I
Iij xi x j 1
Эллипсоид энергии (ЭЭ)
- уравнение поверхности:
суммирование инерций всех
точек по координатам
ЭЭ, расположенный в центре
масс молекулы – центральный
эллипсоид энергии
11
12.
Русакова Н.П.Часть 2
Квантовая механика и квантовая химия
Моменты импульса
Лекция № 7
Эллипсоид энергии
В ЭЭ выбираются три взаимно перпендикулярные оси
таким образом, чтобы недиагональные элементы матрицы тензора момента инерции (содержащие произведение координат) обращались в нуль:
I xy I yx I yz I zy I xz I zx 0
I xx
В этих осях ЭЭ получается
единичную диагональную мат- 0
рицу тензора момента инерции
0
0
I yy
0
0
0 1
I zz 12
13.
Русакова Н.П.Часть 2
Квантовая механика и квантовая химия
Моменты импульса
Лекция № 7
Эллипсоид энергии
Оси ЭЭ, при которых
I xy I yx I yz I zy I xz I zx 0
- главные оси тензора момента инерции: a, b, c.
- диагональные компоненты матрицы Iaa, Ibb, Icc –
главные моменты инерции молекулы
1 2
1 2
2
2
T I ( I aa I bb I cc )
2
2
13
14.
Русакова Н.П.Квантовая механика и квантовая химия
Часть 2
Моменты импульса
Лекция № 7
Потенциальная энергия: U = Uen + Unn + Uee
Для атома Н:
1
Ze
U en
4 0 r
2
Для многоэлектронных атомов:
U эф
Ze
l (l 1)
2
4 0 r
2mr
1
2
2
U = Uэф + Uвал =
= Uэф + (Uen + Unn + Uee)вал
14
15.
Русакова Н.П.Часть 2
Квантовая механика и квантовая химия
Моменты импульса
Лекция № 7
СПАСИБО ЗА ВНИМАНИЕ!
15
16. Задание на усвоение
Фамилия, Имя1. Кинетическая энергия системы
2. Через какую физическую величину можно
связать инерцию с импульсом в квантовой
механике?
3. Тензор момента инерции в системе центра
масс
4. Тензор момента инерции в системе главных
осей
16
17.
Русакова Н.П.Часть 2
Квантовая механика и квантовая химия
Моменты импульса
Лекция № 7
16













 physics
physics








