Напряженно-деформированное состояние

1.

I. НАПРЯЖЕННОДЕФОРМИРОВАННОЕ
СОСТОЯНИЕ
1

2. НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ

• Нормальное σ = Fn/S
и
касательное τ = Ft /S
напряжения
2

3. НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ

• Абсолютная деформация
Δl = lн – lк
ΔV = Vн - V к
Относительная деформация
ε = Δl / lн
ΔV/V = εv
3

4.

НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ
СОСТОЯНИЕ
ns
nt
O
S
2
2
2
ns n t
4

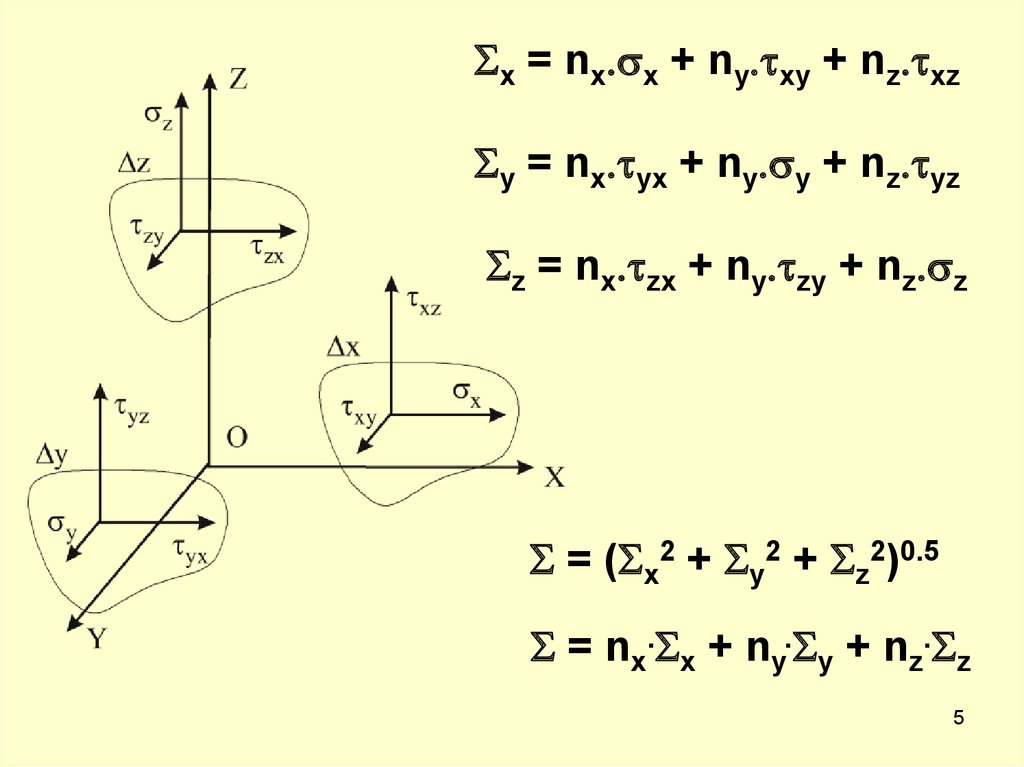
5.

x = nx. x + ny. xy + nz. xz
y = nx. yx + ny. y + nz. yz
z = nx. zx + ny. zy + nz. z
= ( x2 + y2 + z2)0.5
= nx. x + ny. y + nz. z
5

6. Напряженное состояние в точке, физический смысл компонент

х ху хz
,
Tн ух у уz
zx zy z
где
σx, σy, σz – нормальные напряжения
τxy, τxz, τzy – касательные
напряжения
6

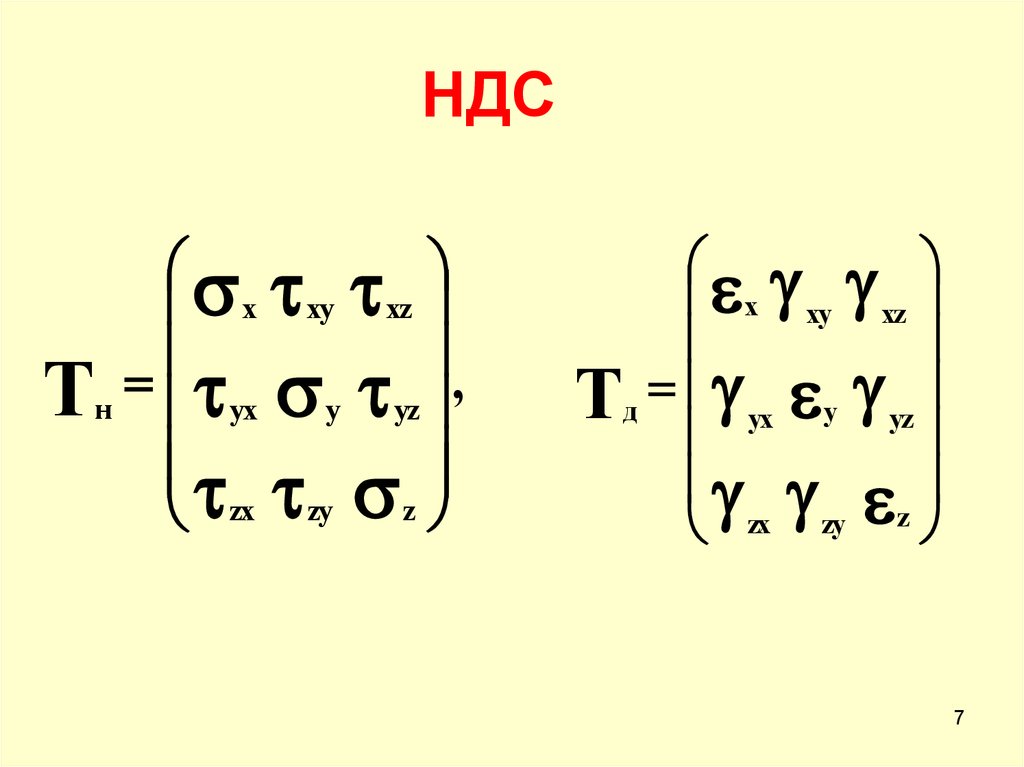
7. НДС

х ху хz
Tн ух у уz ,
zx zy z
х ху хz
Tд ух у уz
zx zy z
7

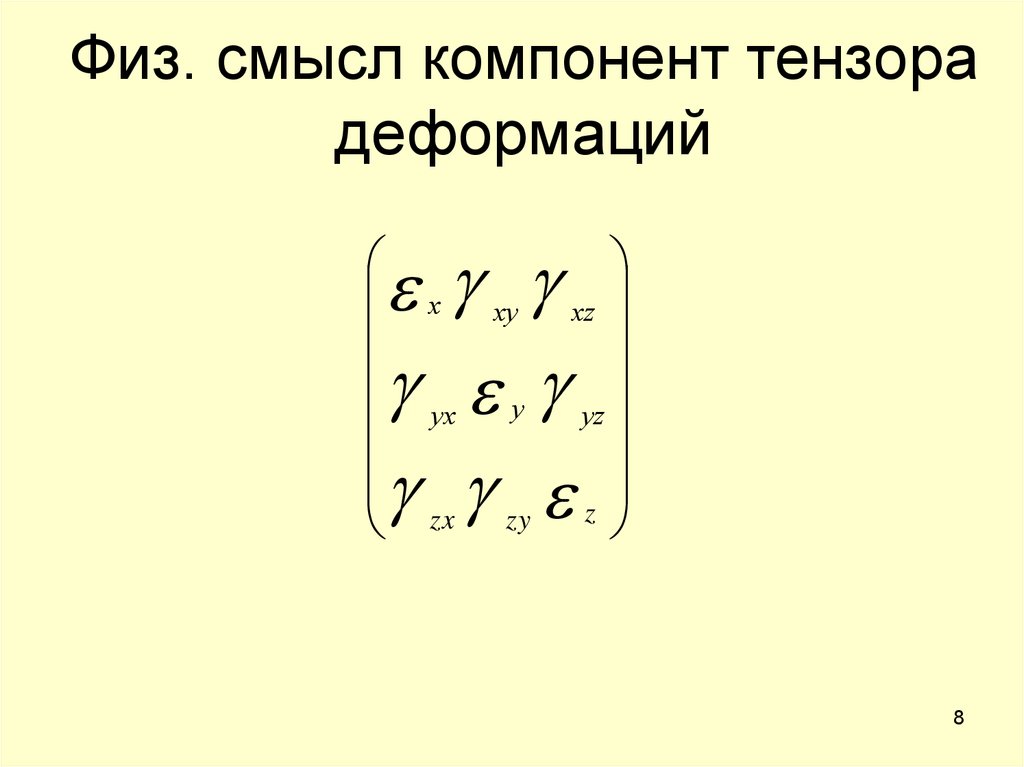
8. Физ. смысл компонент тензора деформаций

х ху хz
ух у уz
zx zy z
8

9. Разложение тензоров

Tн T Т
ш
н
д
н
Tд T T
ш
д
д
д
9

10.

0 0
T 0 0
0 0
ср
ш
ср
Н
Шаровой тензор
ср
0
0
ср
Tдш 0 ср 0
0 0
ср
Тензор-девиатор
( )
T
( )
(
ср
х
ху
хz
Д
Н
ух
zx
ср
у
zy
)
уz
z
ср
х ср
Д
Tд
ух
zx
ху
у
хz
уz
z ср
ср
zy
10

11. Физический смысл компонент

Среднее нормальное
напряжение:
ср
x y z
3
Средняя линейная
относительная
деформация
ср
( z y x )
3
Относительная объемная деформация:
x y z v V / V
11

12. Другой вид тензоров

Главные нормальные
напряжения
12

13. Главные нормальные напряжения

T
í
1 0 0
0 2 0 ,
0 0 3
σ 1 > σ 2 > σ 3,
ср
1 2 3
3
0
0 0
T 0 0 , T 0
0
0 0
0
1
ср
Н
Н
ср
ср
2
0
0
ср
Д
Ш
,
ср
3
ср
13

14. Главные касательные напряжения и их особенности

2 3
1 3
1 2
1
, 2
, 3
,
2
2
2
1 ,
Д
1
2 ,
Д
2
3 ,
Д
3
14

15.

Инварианты
I 1 (Tн ) x y z
I 2 (Tн ) x у y z z x
2
xy
x
xy
xz
I 3 (Тн ) yx
y
yz
zx
zy
z
2
xz
2
yz
15

16. Инварианты тензоров

• В механике разрушения большую роль играют первый инвариант тензора напряжений
I1(Tн) = 1 + 2 + 3
• и второй инвариант девиатора
напряжений:
Д
н
I 2 (T
( )
)
1
2
2
( 2 3 ) ( 1 3 )
,
6
2
2
• Через второй инвариант вводятся понятия
интенсивности напряжений:
16

17. Интенсивности напряжений

i 3I 2 (Т ),
Д
н
i
(
i
2 ) ( 2 3 ) ( 3 1 )
2
2
1
(
i I 2 (T ) ,
д
н
2 ) ( 2 3 ) ( 3 1 )
6
2
1
2
2
2 0,5
,
2 0,5
.
17

18. Вывод

• Напряженное состояние в любой точке
деформируемого тела определено,
если в любой точки этого тела известны
значения среднего нормального
напряжения σср и интенсивности
касательного напряжения τi
18

19. Инвариант и интенсивности деформаций

Д
д
I 2 (T
(
)
2 ) ( 2 3 ) ( 3 1 )
6
2
1
2
2
i 2 I 2 (Т ) / 3
Д
д
i 2 I 2 (Т )
Д
д
19

20. Вывод

• Деформация тела заключается в изменении формы от действия касательных
напряжений и изменении объема под
действием всестороннего давления.
20

21. ГЕОСТАТИЧЕСКОЕ ДАВЛЕНИЕ В ПОРИСТЫХ ГОРНЫХ ПОРОДАХ

• Пористые горные породы всегда насыщены
жидкостью. Пластовое и поровое давления.
Pn ж gH Pрав н. Pг ,
ñð Ðn ,
ýô
Pn
0
0
0
Pn
0
0
0
Pn
21

22. Другой вид тензора деформаций

• Тензору напряжений, записанному через
главные нормальные напряжения, соответствует тензор деформации вида
0
0
1
0
0
TД
2
0 0
3
• ε1 , ε2 , ε3 – главные линейные деформации.
• γ1 = ε2 - ε3 , γ2 = ε1 - ε3 , γ3 = ε1 - ε2 – главные
сдвиги.
22

23. Компоненты нормальных напряжений в координатах: а – прямоугольных; б - цилиндрических

23

24.

Работа упругой деформации
W = (s1e1 + s2e2 + s3e3) / 2,
W = Wф + Wv,
1 = s1 + ср,
2 = s2 + ср,
3 = s3 + ср
1 = e1 + ср,
2 = e2 + ср,
3 = e3 +
ср
Wф = (s1e1 + s2e2 + s3e3) / 2,
24

25.

Wv = 3 ср ср/ 2,
s1 = 2Ge1,
s2 = 2Ge2,
s3 = 2Ge3
ср = K ср,
W = ср2/(2K) + i2/(2G)
25

26. Некоторые вопросы к 1-му рейтингу

• Строение тензора напряжений, физический смысл
компонент.
• Шаровой тензор и тензор-девиатор; физический
смысл разложения тензора напряжений на эти
слагаемые.
• Изменение объема и формы «точки»; что
обеспечивает и то и другое?
• Главные касательные напряжения.
• Строение тензора деформаций, физический смысл
компонент.
• Шаровой тензор деформаций и тензор-девиатор
деформаций; физический смысл разложения тензора
деформаций на эти слагаемые.
26

27. Некоторые вопросы к 1-му рейтингу

• Тензор напряжений через главные нормальные
напряжения
27