Центральные и вписанные углы

1. Центральные и вписанные углы

ЦЕНТРАЛЬНЫЕ И
ВПИСАННЫЕ
УГЛЫ
Геометрия
8 класс

2. Цели урока:

ЦЕЛИ УРОКА:
Познакомиться с понятием центрального угла.
Познакомиться с понятием вписанного угла.
Установить связь между градусными мерами
центрального и вписанного углов,
опирающихся на одну и ту же дугу.

3. Центральный угол

ЦЕНТРАЛЬНЫЙ УГОЛ
Угол с вершиной в центре
окружности называется
центральным углом.
Если дуга АВ меньше
полуокружности или
является полуокружностью,
то её градусная мера
считается равной градусной
мере центрального угла
АОВ. Если же дуга больше
полуокружности, то её
градусная мера равна
360º - АОВ.

4. Вписанный угол

ВПИСАННЫЙ УГОЛ
Угол,
вершина
которого лежит на
окружности, а
стороны пересекают
окружность,
называется
вписанным углом.

5. Теорема о вписанном угле

ТЕОРЕМА О ВПИСАННОМ УГЛЕ
Вписанный угол равен половине дуги, на
которую он опирается.

6. Следствие 1

СЛЕДСТВИЕ 1
Вписанные
углы,
опирающиеся на одну
и ту же дугу, равны.

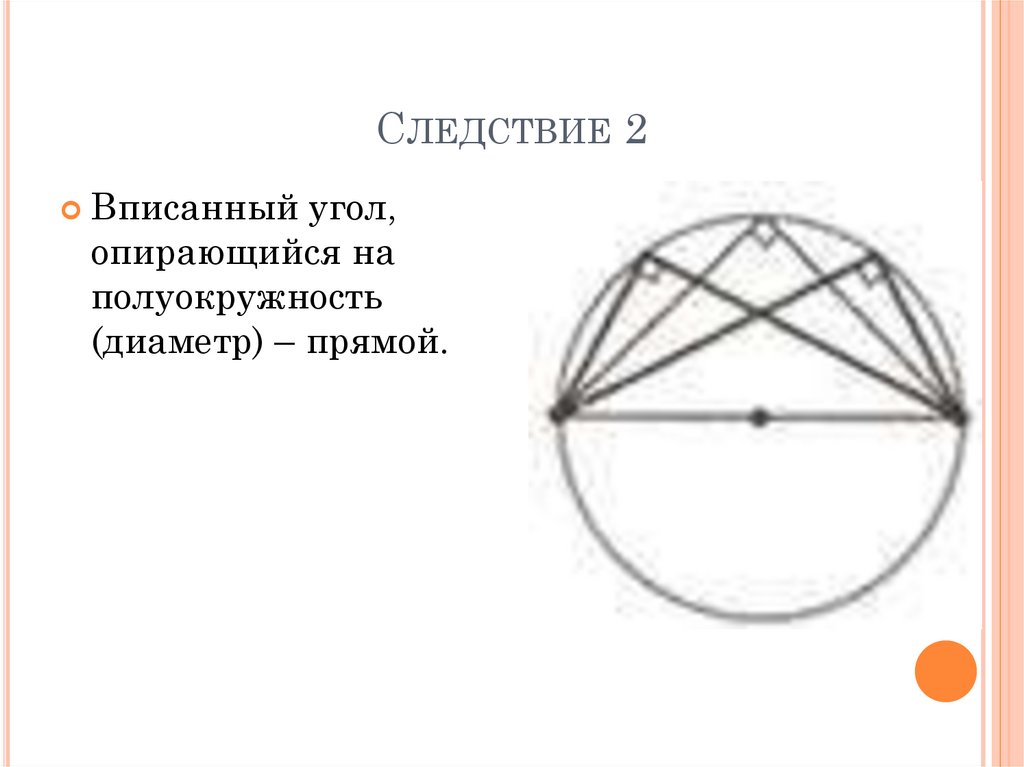
7. Следствие 2

СЛЕДСТВИЕ 2
Вписанный
угол,
опирающийся на
полуокружность
(диаметр) – прямой.

8. Установите связь между центральным и вписанным углами, опирающимися на одну и ту же дугу.

ЦЕНТРАЛЬНЫМ И ВПИСАННЫМ
УГЛАМИ, ОПИРАЮЩИМИСЯ НА ОДНУ
И ТУ ЖЕ ДУГУ.

9.

Определите
неизвестные углы.

10. Домашнее задание:

ДОМАШНЕЕ ЗАДАНИЕ:
§2, №650, 654.