Similar presentations:
Возведение в квадрат суммы и разности двух выражений
1.
ПРЕЗЕНТАЦИЯ К УРОКУ ПО ТЕМЕ:«ВОЗВЕДЕНИЕ
В КВАДРАТ СУММЫ И РАЗНОСТИ
ДВУХ ВЫРАЖЕНИЙ»
Плехова Людмила Анатольевна,
учитель математики МБОУ
«СОШ п. Нивенское»
Багратионовский район
Калининградская область
2.
ПСИХОГЕОМЕТРИЯ3.
Цели урока:Образовательные:
-вывести формулы квадратов суммы и разности двух чисел;
-сформировать умение учащихся практически применять эти формулы для
упрощения выражений, рационального вычисления числовых выражений.
Развивающие :
-развивать логическое мышление, внимание, память, сообразительность,
культуру математической речи и культуру общения.
Воспитывающие:
-воспитывать ответственное отношение к деятельности, высокой
познавательной активности и самостоятельности;
-воспитывать интерес к математике как учебному предмету через
современные технологии преподавания;
- воспитывать чувство ответственности.культуры диалога.
4.
Эпиграф урока:Знание только тогда знание,
когда оно приобретено усилиями
своей мысли, а не памятью.
(Л.Н.Толстой)
5.
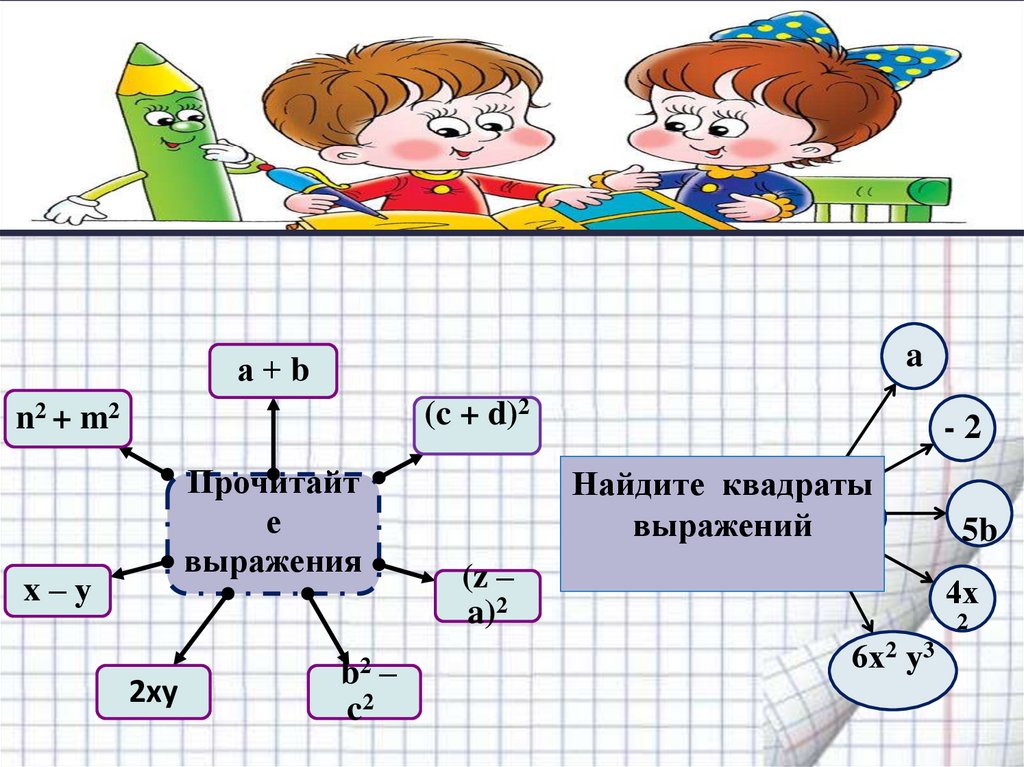
aа+b
(c + d)2
n2 + m2
Прочитайт
е
выражения
x–у
2ху
b2
c2
-2
Найдите квадраты
выражений
(z –
a)2
–
5b
4х
2
6х2 у3
6.
36а225x4
х6с8
100
64
Представьте
в виде
квадрата
49 b2c2
7.
а и bНайдите
3b и -5с
удвоенное
произведение
выражений
0,4х и 2х2
0,5y и 6
8.
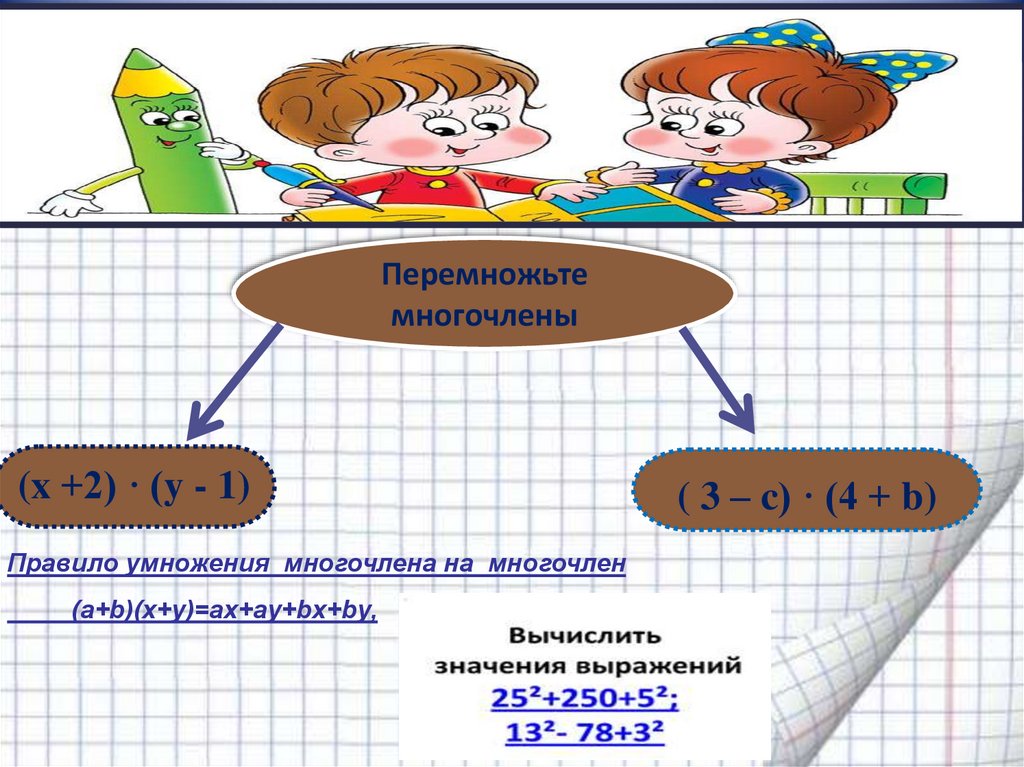
Перемножьтемногочлены
(x +2) · (y - 1)
Правило умножения многочлена нa многочлен
(a+b)(x+y)=ax+ay+bx+by,
( 3 – c) · (4 + b)
9.
1 вариант• (y + b) (y +b)
• (с + d ) (c +d)
• (х + 2) (х+2)
2 вариант
• (x – y) (x – y)
• (m - n) (m- n)
• (a – 2) (a – 2)
К плану
10.
ИССЛЕДОВАТЕЛЬСКАЯРАБОТА
№
I
II
(y + b) 2
(c + d)2
(х + 2)2
III
y 2 + 2yb + b2
c2 + 2cd + d2
х2 + 4х + 4
x2 – 2xy + y2
m2 – 2mn + n2
a2 – 4a + 4
1.
(y + b) (y +b)
2.
(с + d ) (c +d)
3.
(х + 2)(х+2)
4.
(x – y) (x – y)
5.
(m - n) (m- n)
(x – y)2
(m - n)2
6.
(a – 2)(a – 2)
(a – 2)2
11.
ПРОВЕРКА(6х + y) 2 = 36х2 + 12xy + y2
(
(5 - 4b) 2 = 25 - 40b + 16b2
12.
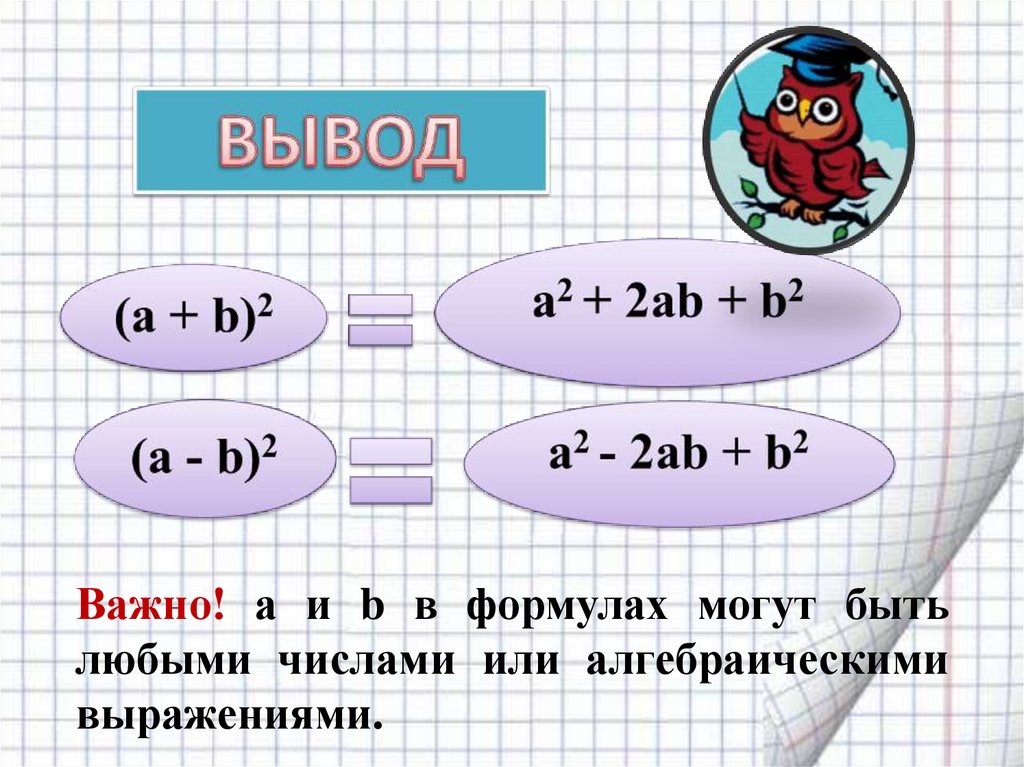
Важно! а и b в формулах могут бытьлюбыми числами или алгебраическими
выражениями.
13.
(а + b)2 =а2 + 2аb +b2(а - b)2 =а2 - 2аb+b2
Квадрат суммы двух
выражений равен
Квадрат разности двух
выражений равен
квадрату первого выражения
квадрату первого выражения
плюс удвоенное произведение минус удвоенное произведение
первого и второго выражений
первого и второго выражений
плюс
квадрат
выражения
второго плюс
квадрат
выражения
второго
14.
ПРИМЕРЫ15.
,К плану
16.
Заполнить таблицуВыражение
Квадрат
1
выражения
Удвоенное
произведение
Квадрат
2
выражения
Итог
(а + 4)2
а2
8а
16
а2 + 8а + 16
(8 - х)2
64
16х
х2
64-16х + х2
(2y + 1)2
4у2
4у
1
4у2 + 4у + 1
(0,5b - 2)2
0,25b2
2b
4
0,25b2 –2b + 4
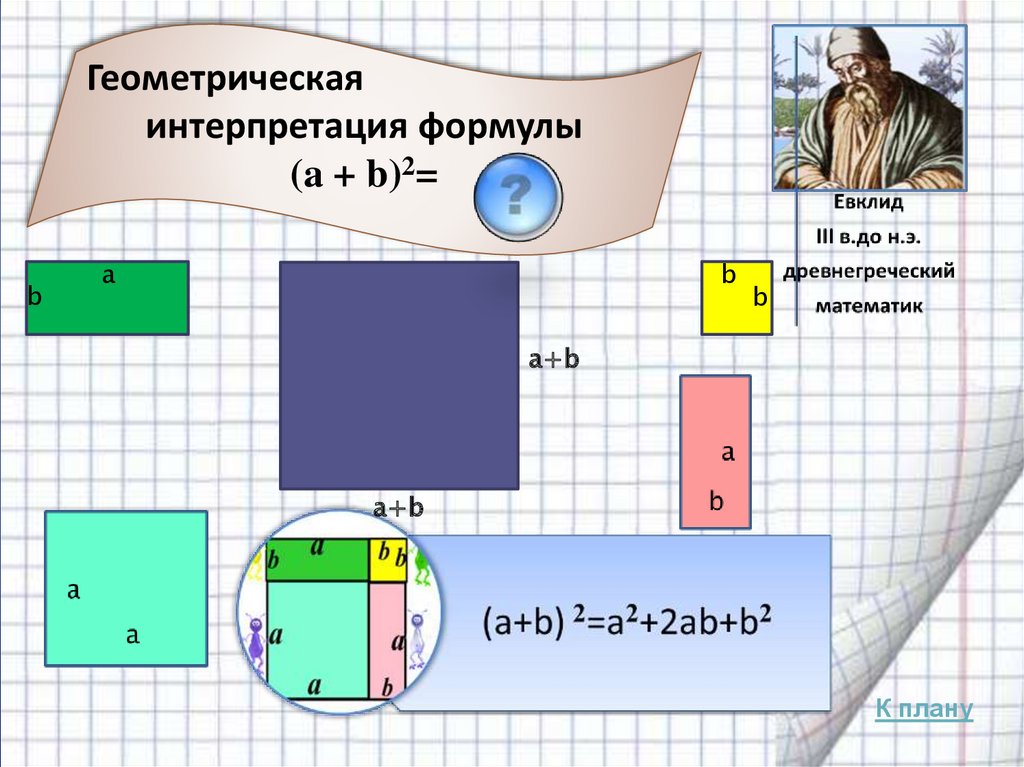
17.
Геометрическаяинтерпретация формулы
(a + b)2=
b
a
b
b
a+b
a+b
К плану
18.
1)( a b) a ab b ;2
2
2
2)( a b) a b 2ab;
2
2
2
3)( x y ) x 2 xy y;
2
2
4)( p q ) p 2 pq q ;
2
2
2
5)( m n) m n 2mn;
2
2
2
6)( c d ) 2 c 2 cd d 2 ;
7)(b 3) 9 6b b ;
2
2
8)( x 5) x 10 x 25;
2
2
9)(9 y ) 2 81 18 y y 2 ;
10)( c 10) 20c c 100.
2
2
19.
Формулы сокращённого умноженияприменяются в некоторых случаях для
упрощения вычислений. Например:
99 100 1 100 2 100 1 1 10000 200 1 9801
2
2
1. Вычислить:
(30+1) 2
(30-1) 2
2
2
512
492
20.
ПРОВЕРКА21.
3. Преобразуйте выражения:(а-7) 2
( 5+х) 2
(7-а) 2
(-5-х) 2
22.
(а - b)2 = (b - а)2(-а - b)2 =(а + b)2
ПРОВЕРКА
25²+250+5²=(25+5) ²=30²=900
13²- 78+3² =(13-3)²=10²=100
К плану
23.
САМОСТОЯТЕЛЬНАЯ РАБОТАА. Представить в виде многочлена:
2 ВАРИАНТ
1 ВАРИАНТ
а) 3 х ;
а ) 2 х ;
2
2
б ) а 6 ;
б ) b 3 ;
2
2
в ) 2 х 1 ;
в ) 4 х 1 ;
2
2
г ) 3х 4 у ;
г ) 2 х 3 у ;
2
2
В. Вычислите:
2
д) х 5 .
1 ВАРИАНТ
2
2
д) х 5 .
2
2 вариант
а)792 ; б )1012.
а)392 ; б )1032.
С. Представить в виде квадрата двучлена:
2ВАРИАНТ
1 ВАРИАНТ
a)4 p 2 4ap a 2 ;
а)4а 4аb b ;
2
2
2
2
б
)
49
n
14
nm
m
.
б )36 p 12 px x .
2
2
24.
ПРОВЕРКАА. Представить в виде многочлена:
2 вариант
1 вариант
а)4 4 х х ;
а )9 6 х х 2 ;
б )b 6b 9;
б )а 2 12а 36;
в )16 x 8 x 1;
в )4 х 2 4 х 1;
2
2
2
г )9 х 2 24 ху 16 у 2 ;
г )4 x 12 xy 9 y ;
2
2
д) х 4 10 х 2 25.
д) x 10 x 25.
4
В. Вычислите:
2 вариант
1 вариант
а )79 2 80 1 6400 160 1 6241;
2
2
а)392 (40 1) 2 1600 80 1 1521;
б )1012 100 1 10000 200 1 10201. б )1032 (100 3) 2 10000 600 9 10609.
2
С. Представить в виде квадрата двучлена:
1 вариант
а ) 2 а b ;
2
б ) 6 p x .
2
2 вариант
2
a ) 2 p a ;
2
б ) 7 n m .
25.
Критерии оценок:«5», если правильно 8-9;
Вы молодец!
«4», если правильно 6-7;
Чуть внимательнее!
«3», если правильно 4-5.
Вы сегодня не настроились
на работу.
26.
-С какими формулами мы познакомились сегодня на уроке?-Почему эти формулы называются формулами сокращенного умножения?
-Чему равен квадрат суммы двух выражений?
-Чему равен квадрат разности двух выражений?
-Как вы думаете, зачем нужны нам эти формулы и стоит ли их запоминать?
- Понравился ли вам урок?
Домашнее задание.
Выучить правила и формулы квадрата суммы и квадрата разности, п.
32.
На оценку «3» : № 800, 803(а,б,в), 810а-г
На оценку «4,5»: № 804, 808, 810д-з
формулы (a-b)2.
,
доказать геометрический смысл
Выставление оценок.






















 mathematics
mathematics








