Similar presentations:
Программа TINA 9.0
1.
Лекция 32022
1
2.
Программа TINA 9.0Toolkit for Interactive Network Analysis
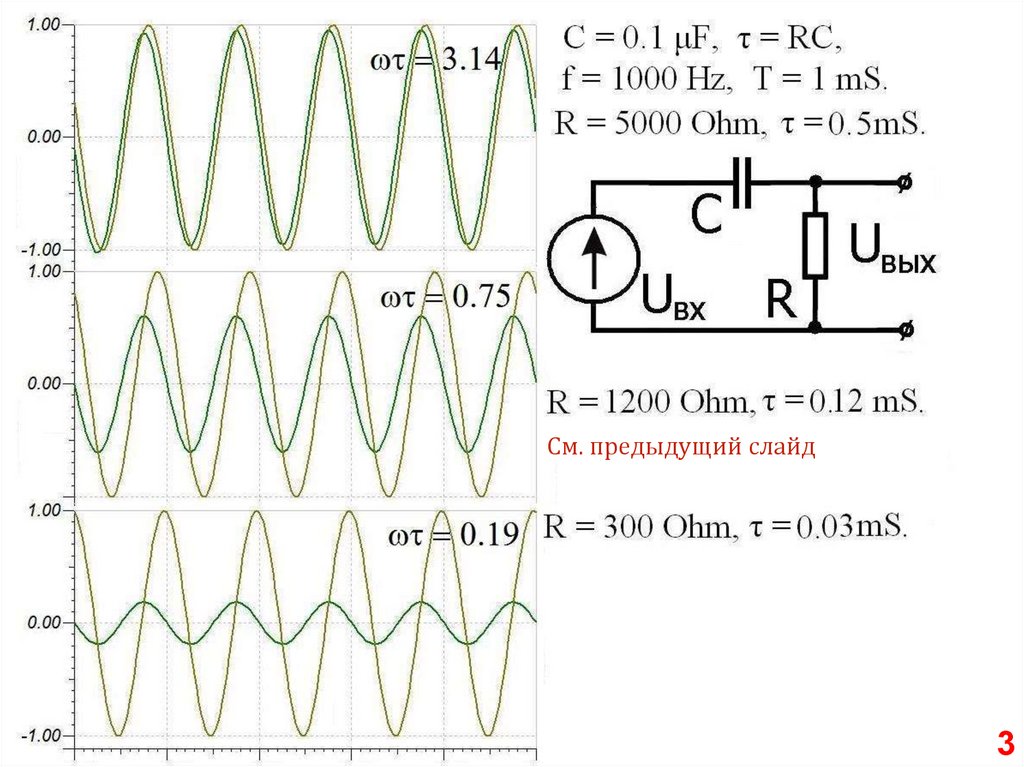
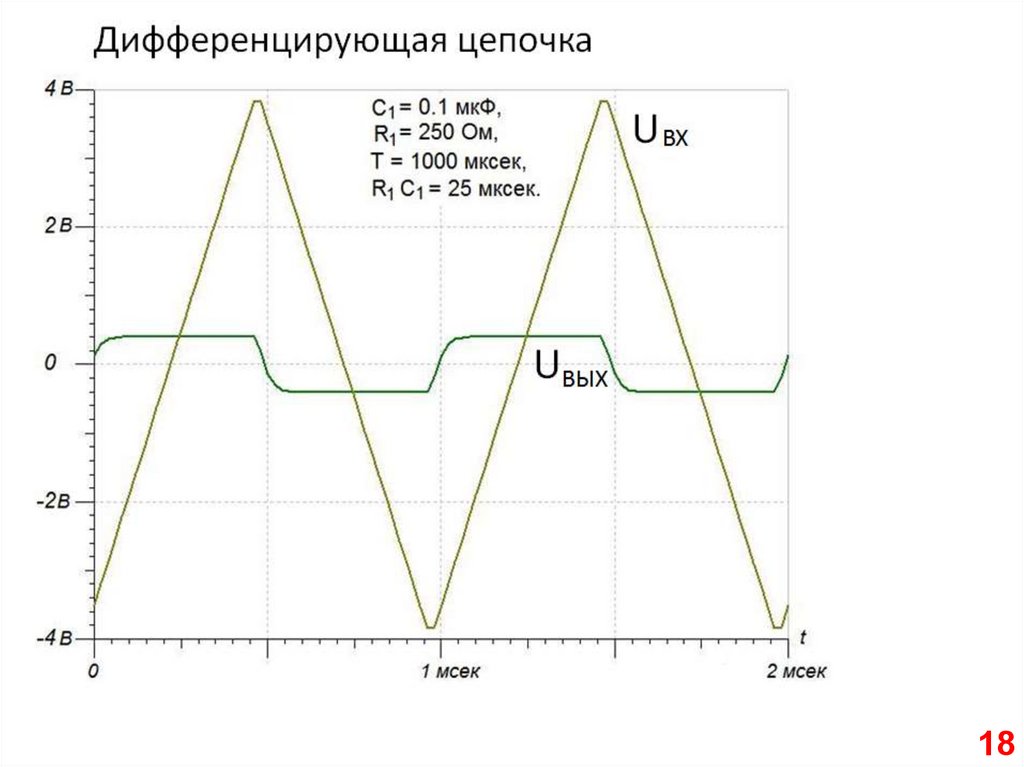
Дифференцирующая цепочка
7.07 5.65 4.26
9.91
!
2
3.
См. предыдущий слайд3
4.
45.
56.
67.
78.
89.
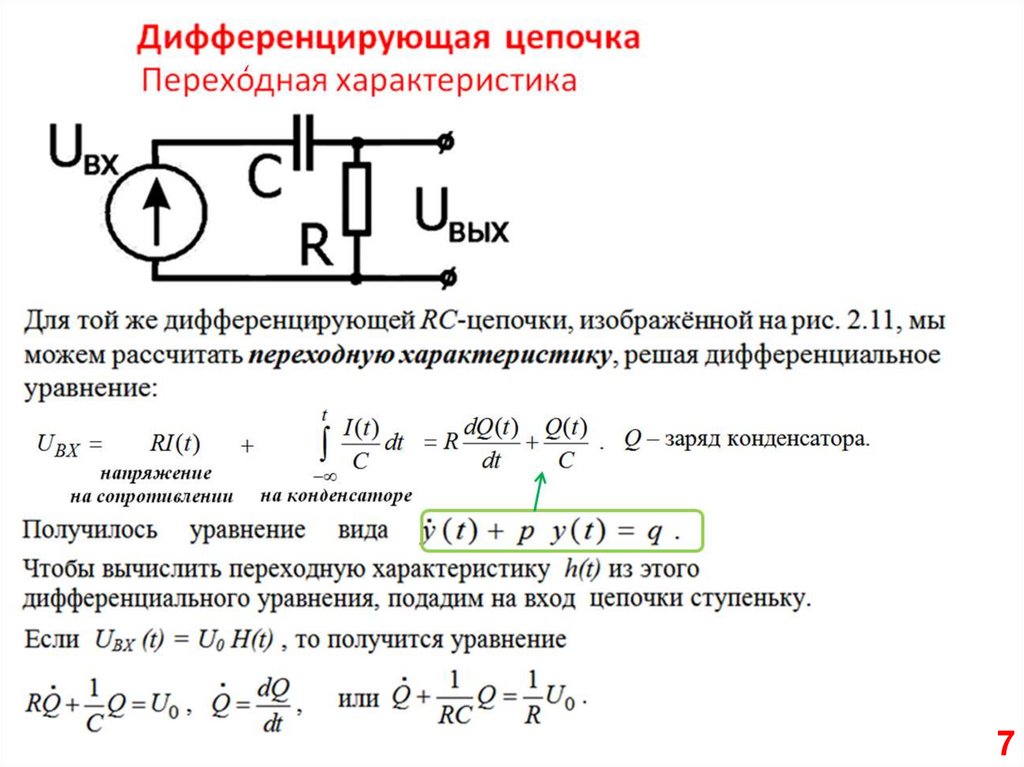
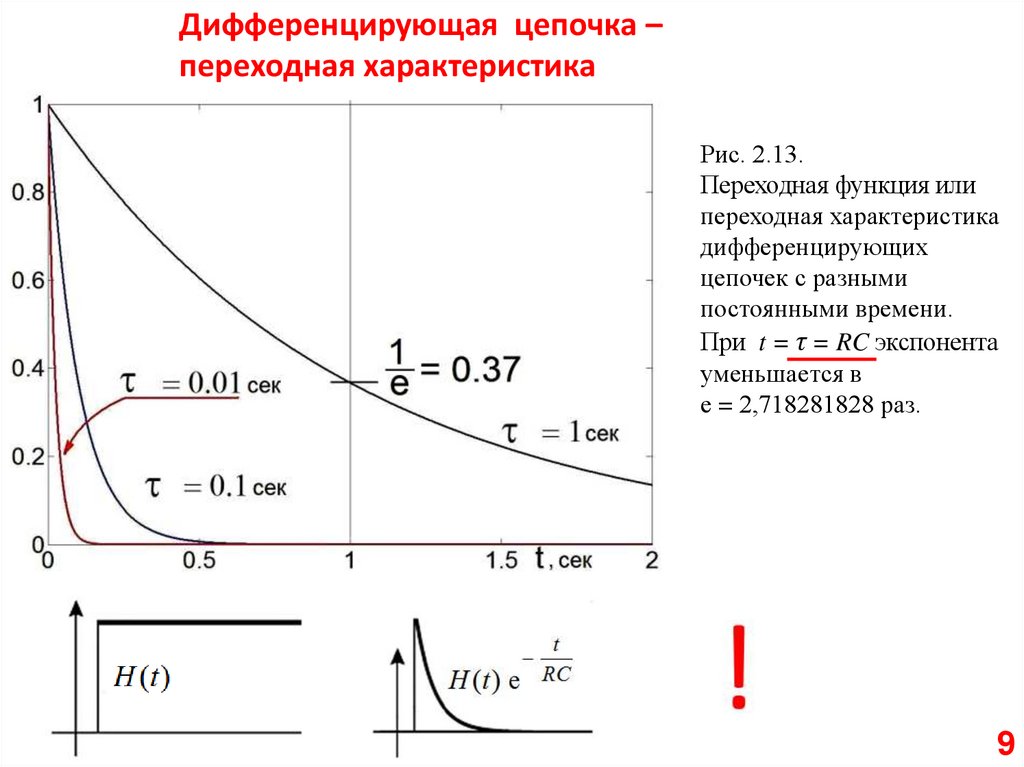
Дифференцирующая цепочка –переходная характеристика
Рис. 2.13.
Переходная функция или
переходная характеристика
дифференцирующих
цепочек с разными
постоянными времени.
При t = τ = RC экспонента
уменьшается в
е = 2,718281828 раз.
9
10.
Рис. 2.11.10
11.
1112.
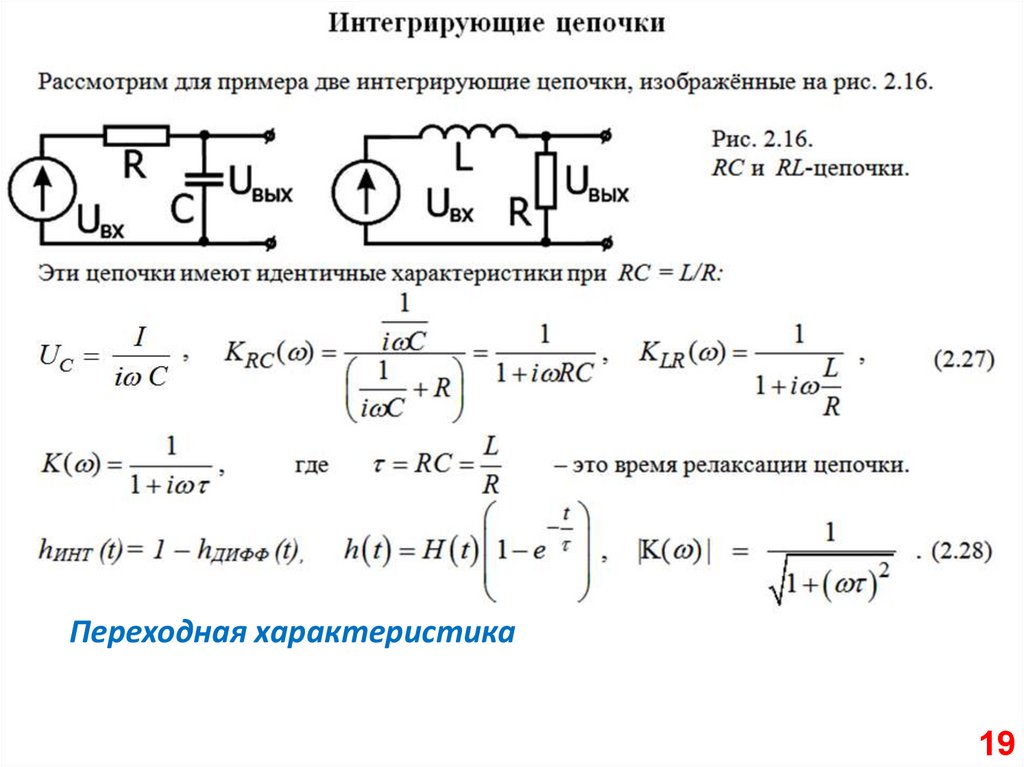
RCRL
12
13.
, K ( ) 1; 0, K ( ) i .13
14.
1415.
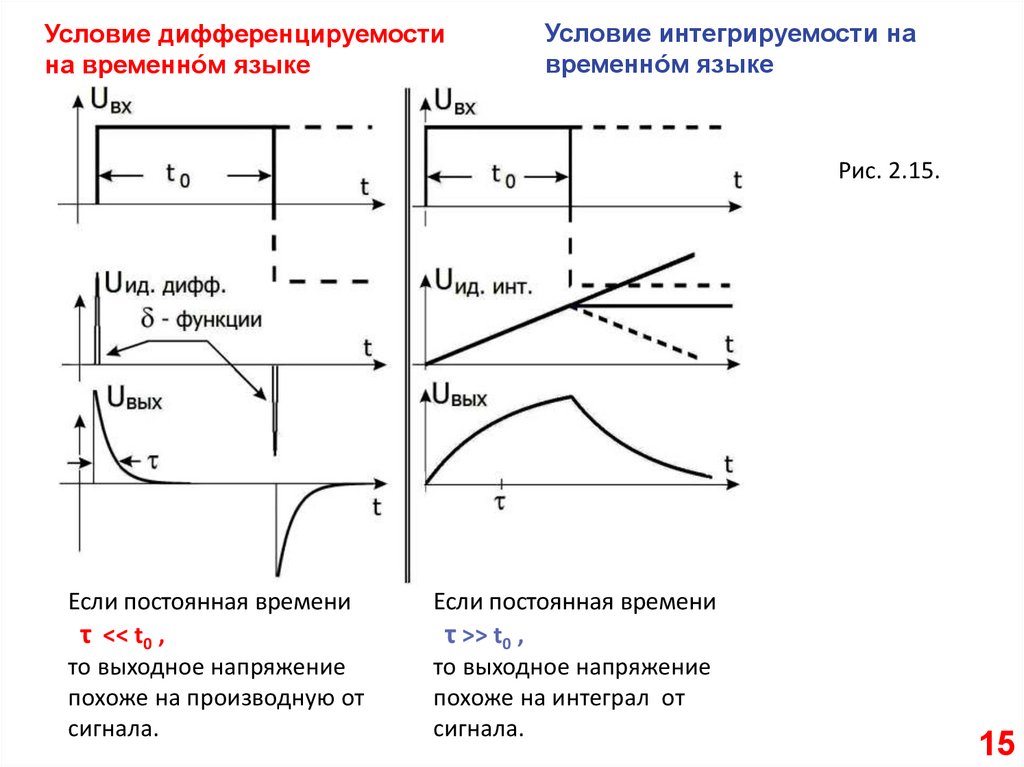
Условие дифференцируемостина временно́м языке
Условие интегрируемости на
временно́м языке
Рис. 2.15.
Если постоянная времени
τ << t0 ,
то выходное напряжение
похоже на производную от
сигнала.
Если постоянная времени
τ >> t0 ,
то выходное напряжение
похоже на интеграл от
сигнала.
15
16.
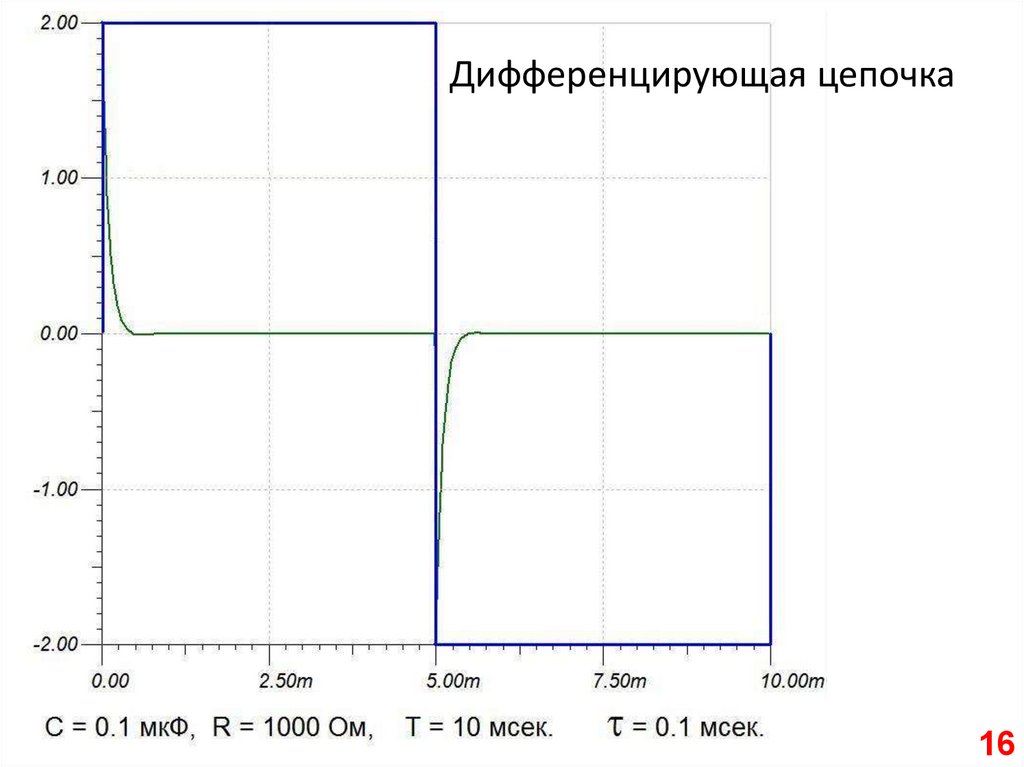
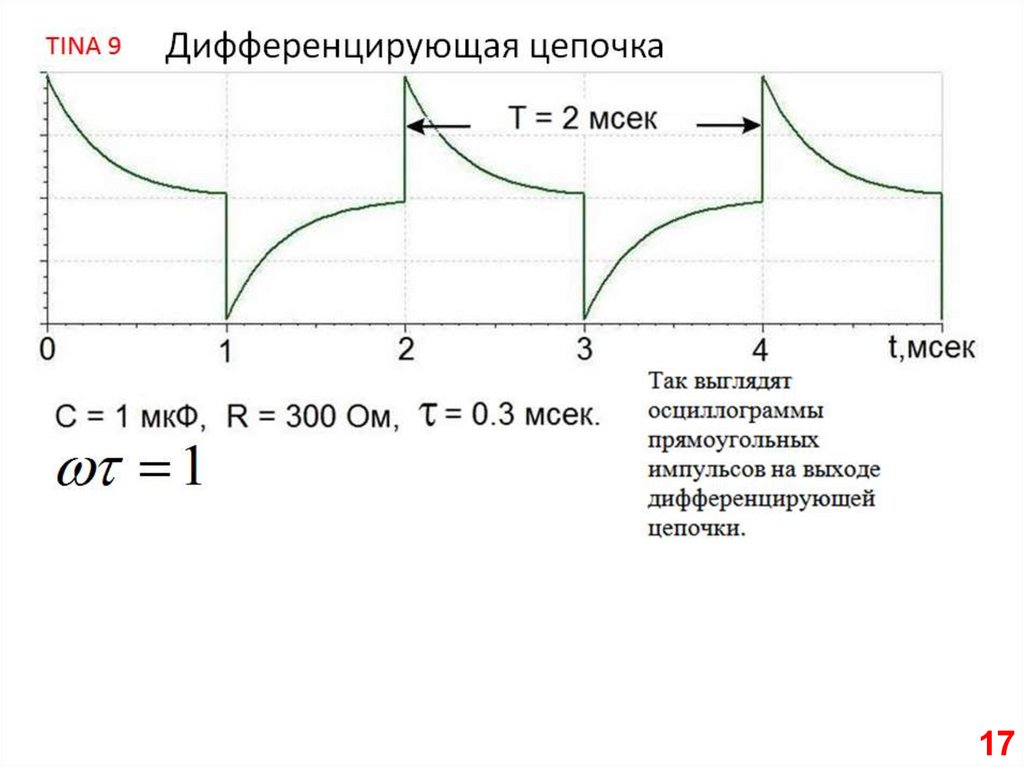
Дифференцирующая цепочка16
17.
1718.
1819.
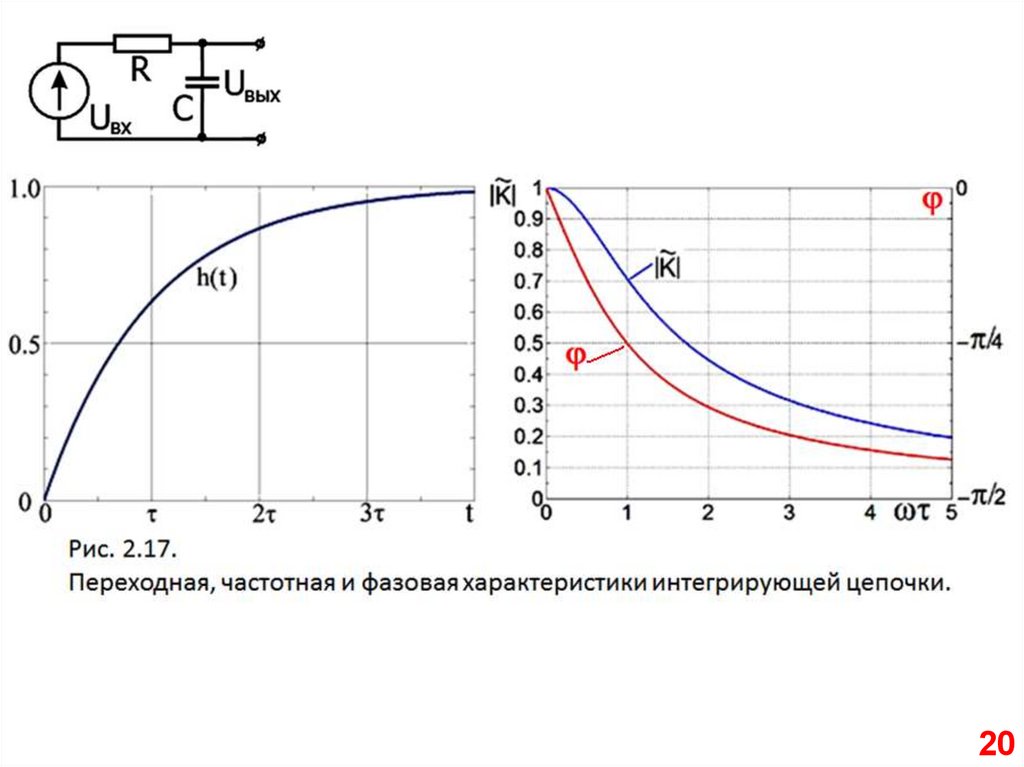
Переходная характеристика19
20.
2021.
2122.
2223.
2324.
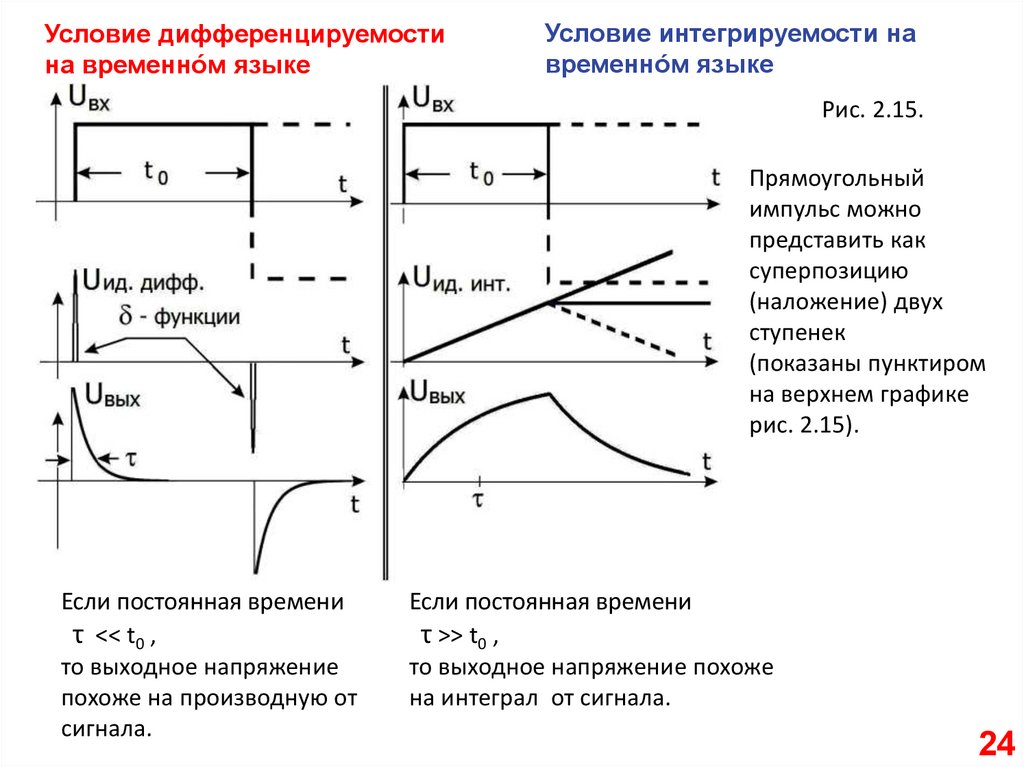
Условие дифференцируемостина временно́м языке
Условие интегрируемости на
временно́м языке
Рис. 2.15.
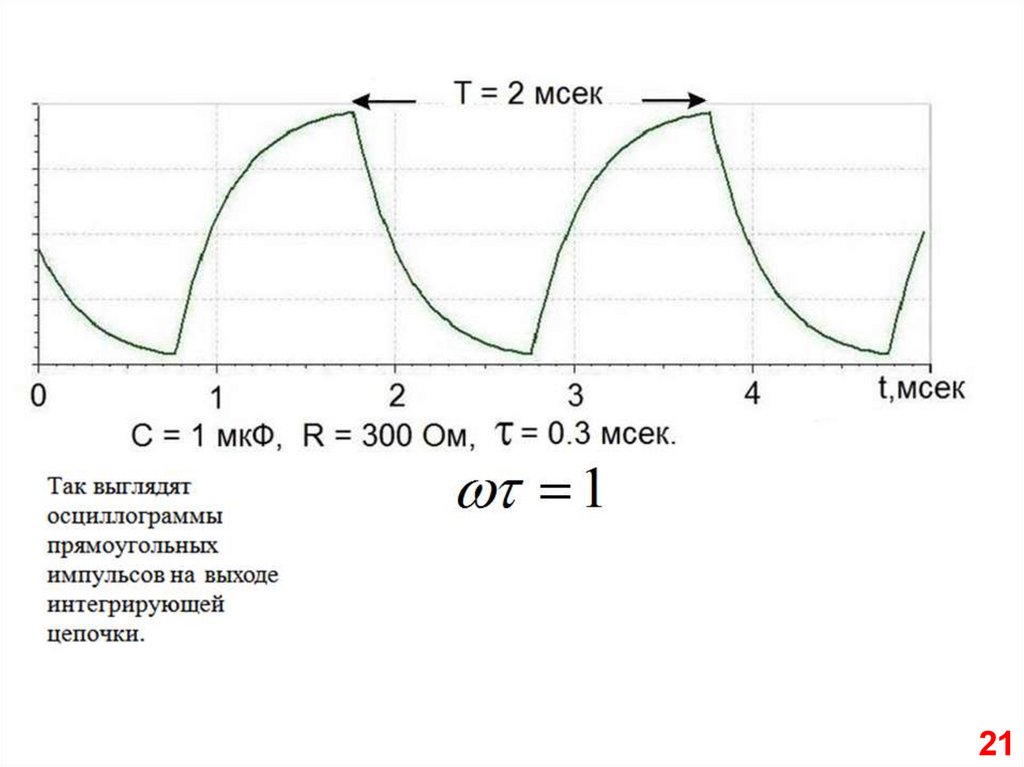
Прямоугольный
импульс можно
представить как
суперпозицию
(наложение) двух
ступенек
(показаны пунктиром
на верхнем графике
рис. 2.15).
Если постоянная времени
τ << t0 ,
то выходное напряжение
похоже на производную от
сигнала.
Если постоянная времени
τ >> t0 ,
то выходное напряжение похоже
на интеграл от сигнала.
24
25.
2526.
2627.
2728.
2829.
2 2 i 02 0 .Решая это квадратное уравнение и используя начальные условия, получим:
1,2 i 0
2
где
2
i 01,
01 0 ,
2
I (t ) A1e
i 1t
A2e
A1e
t i 01t
A1e
( i 01 )t
2
i 2t
A2e
t i 01t
A2e
( i 01 )t
, *
29
30.
*i
i
30
31.
3132.
3233.
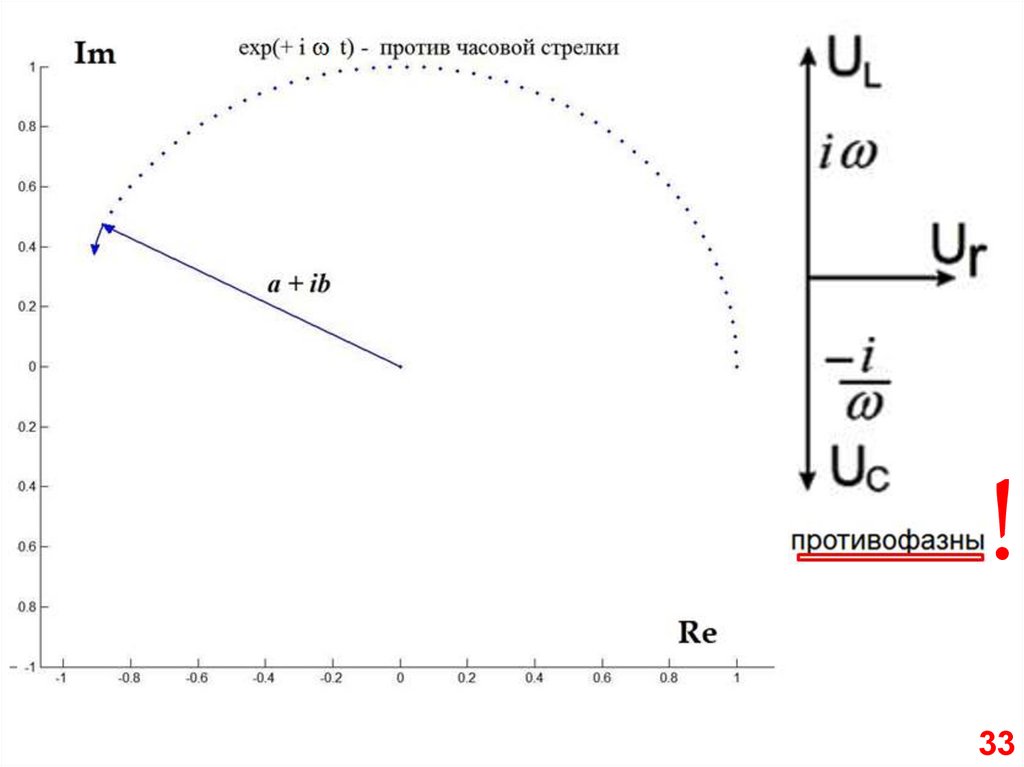
!33
34.
3435.
e35
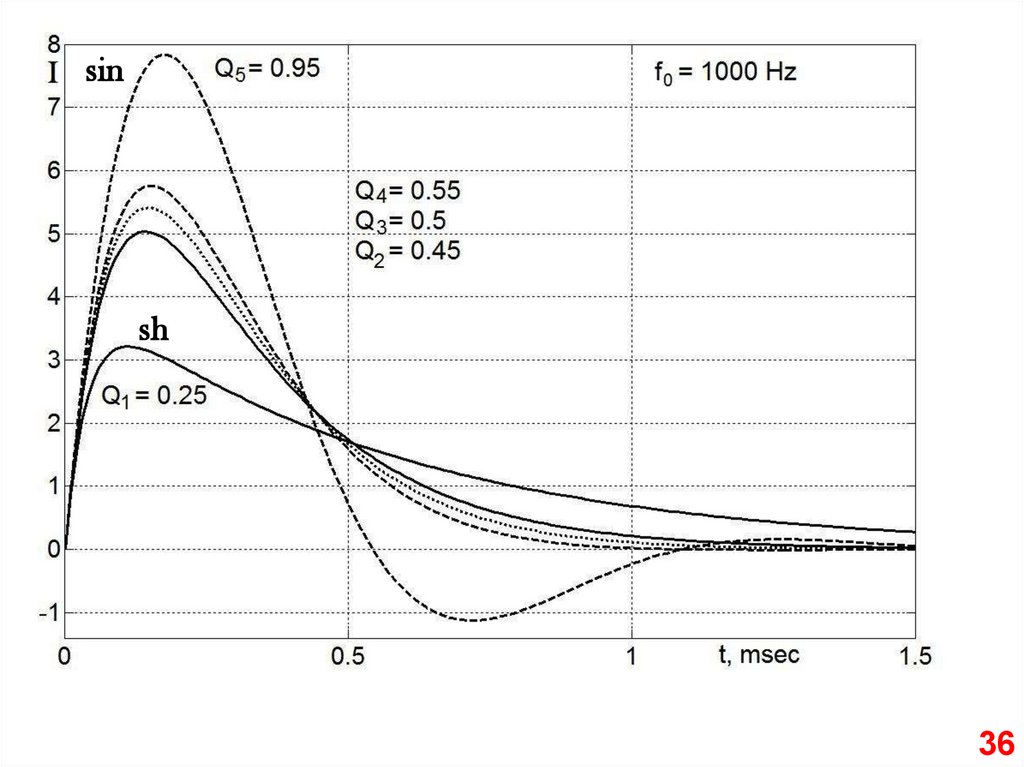
36.
sinsh
36
37.
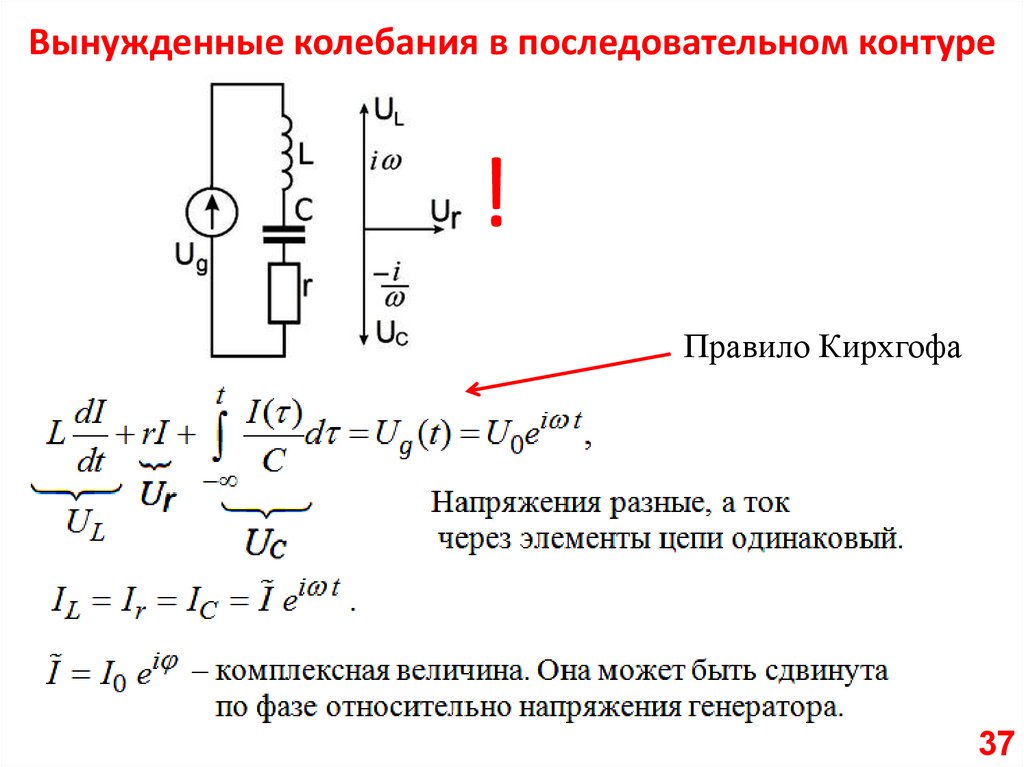
Вынужденные колебания в последовательном контуре!
Правило Кирхгофа
37
38.
3839.
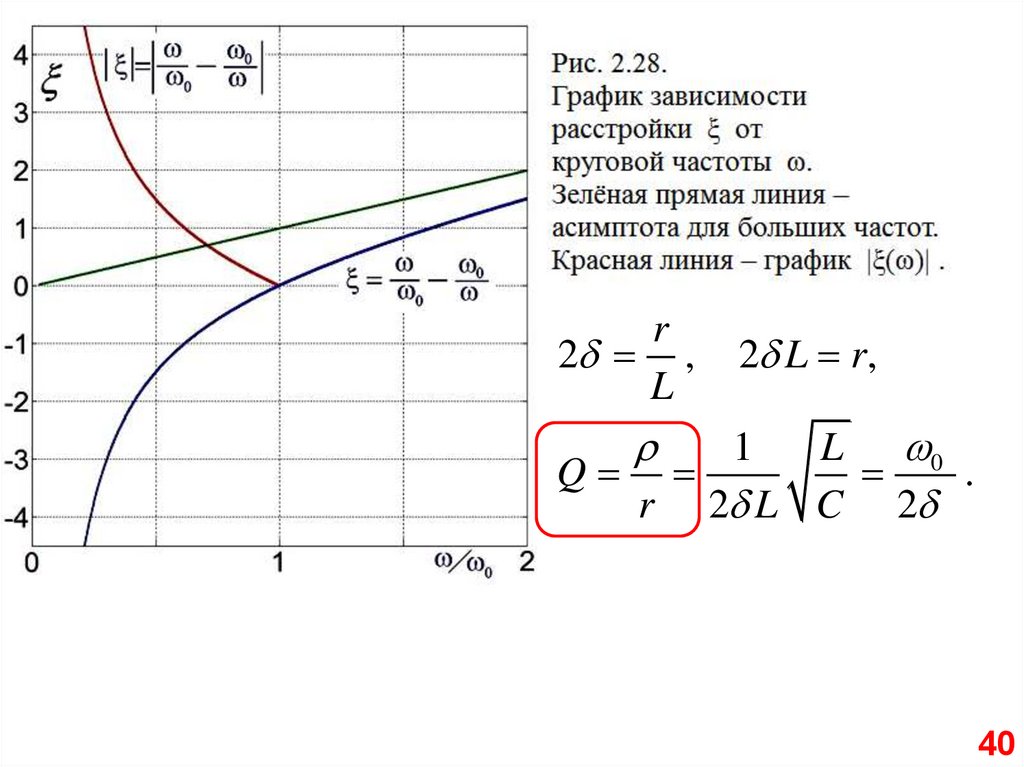
3940.
r2 ,
L
2 L r,
L 0
Q
.
r 2 L C 2
1
40
41.
(2.42)Q
r
(2.43)
см. (2.39)
39 слайд
41
42.
4243.
(2.44)43
44.
!Сумма напряжений на ёмкости и индуктивности равна нулю,
p.t.o.
а импеданс контура минимален и равен r. В этом случае
фазы колебаний напряжений UL и UC таковы, что они
компенсируют друг друга – это называется резонансом напряжений.
На резонансе амплитуды напряжений UL и UC в Q раз больше напряжения
генератора!
44
45.
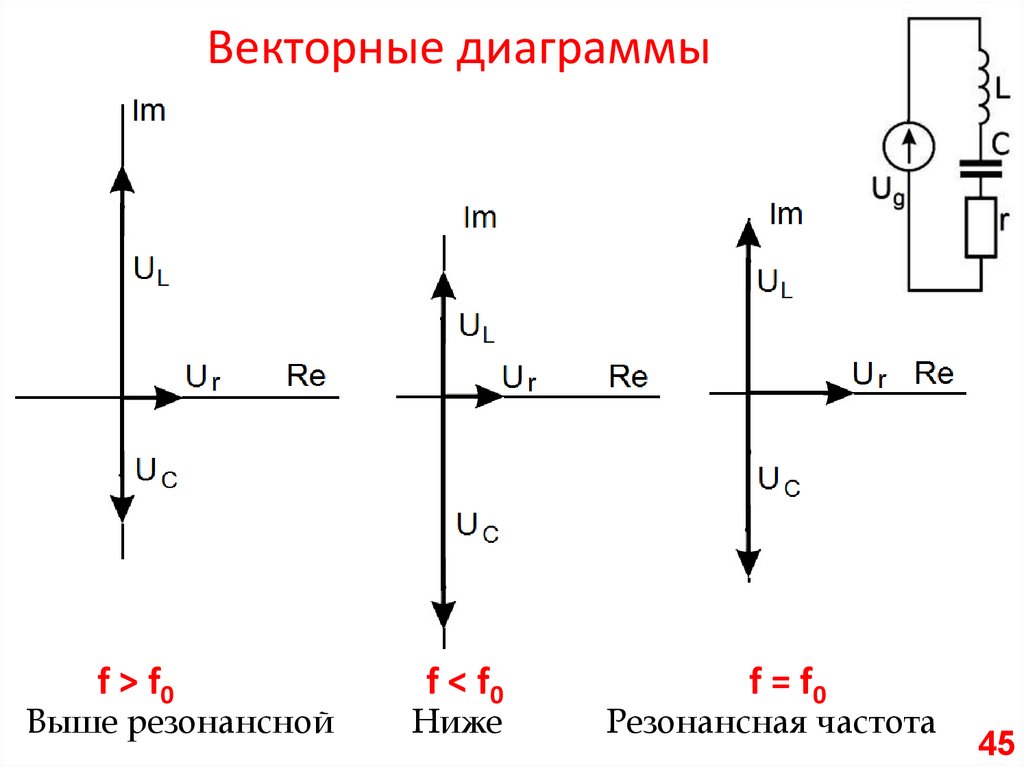
Векторные диаграммыf > f0
Выше резонансной
f < f0
Ниже
f = f0
Резонансная частота
45
46.
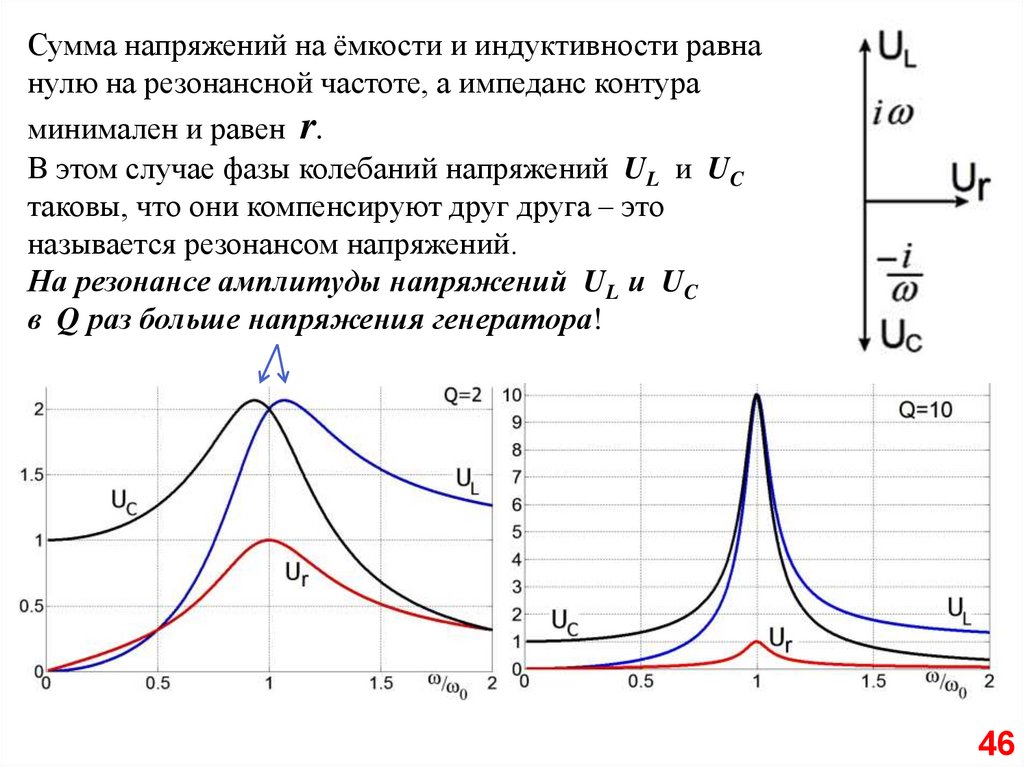
Сумма напряжений на ёмкости и индуктивности равнанулю на резонансной частоте, а импеданс контура
минимален и равен r.
В этом случае фазы колебаний напряжений UL и UC
таковы, что они компенсируют друг друга – это
называется резонансом напряжений.
На резонансе амплитуды напряжений UL и UC
в Q раз больше напряжения генератора!
46
47.
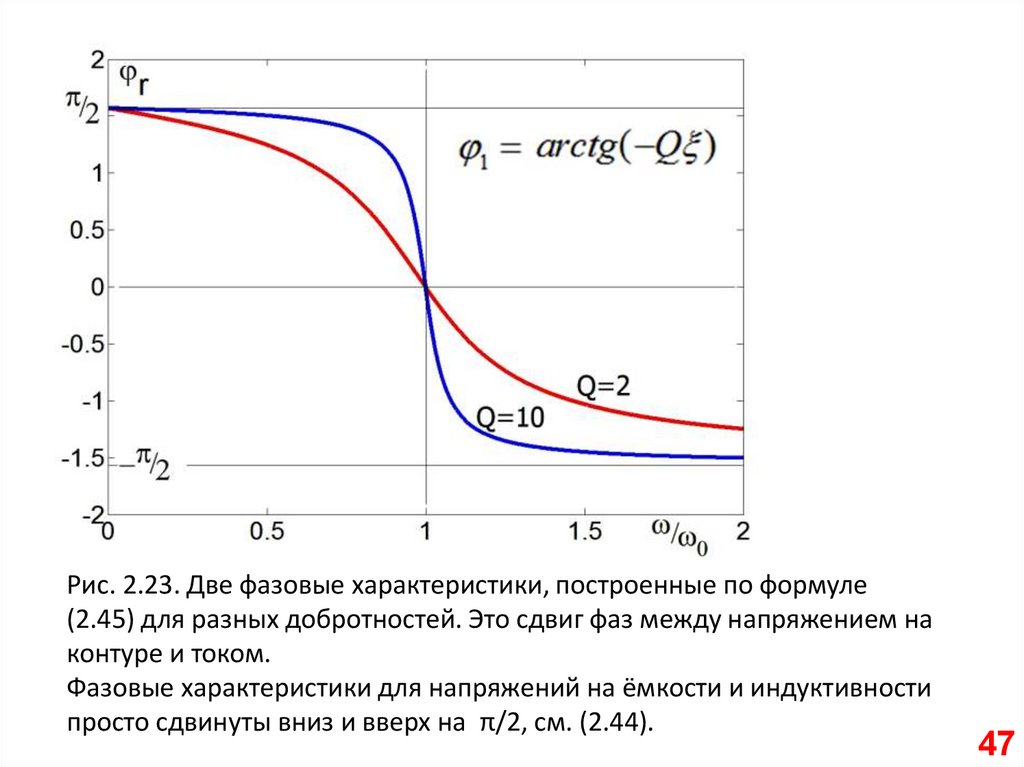
Рис. 2.23. Две фазовые характеристики, построенные по формуле(2.45) для разных добротностей. Это сдвиг фаз между напряжением на
контуре и током.
Фазовые характеристики для напряжений на ёмкости и индуктивности
просто сдвинуты вниз и вверх на π/2, см. (2.44).
47
48.
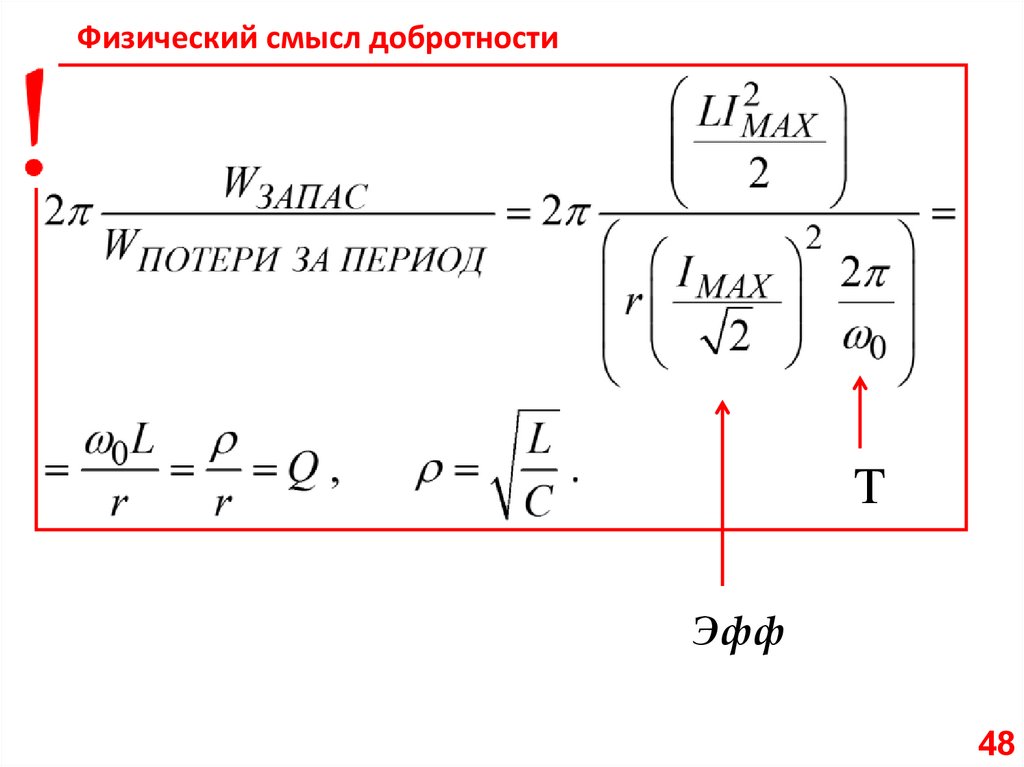
Физический смысл добротностиT
Эфф
48
49.
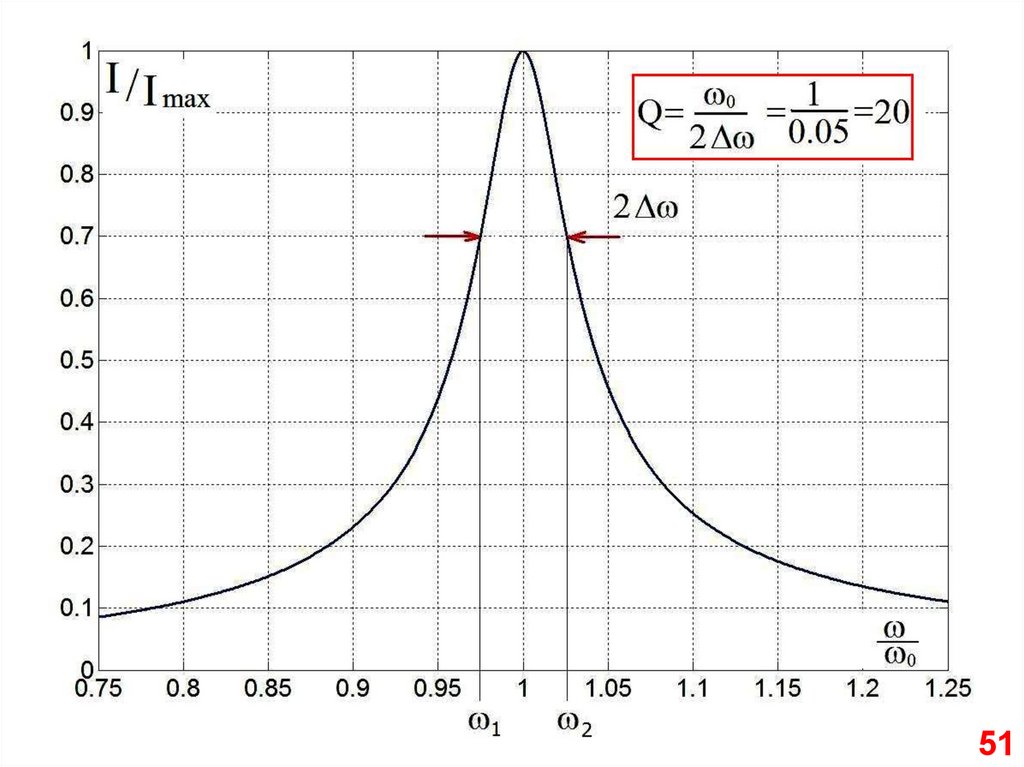
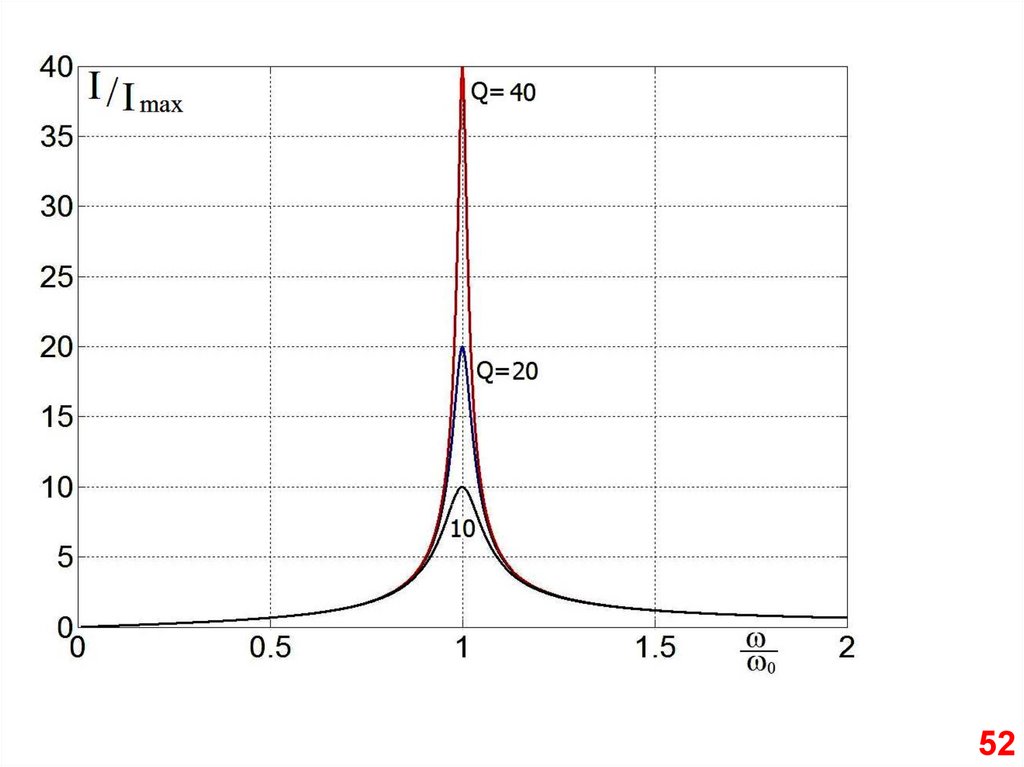
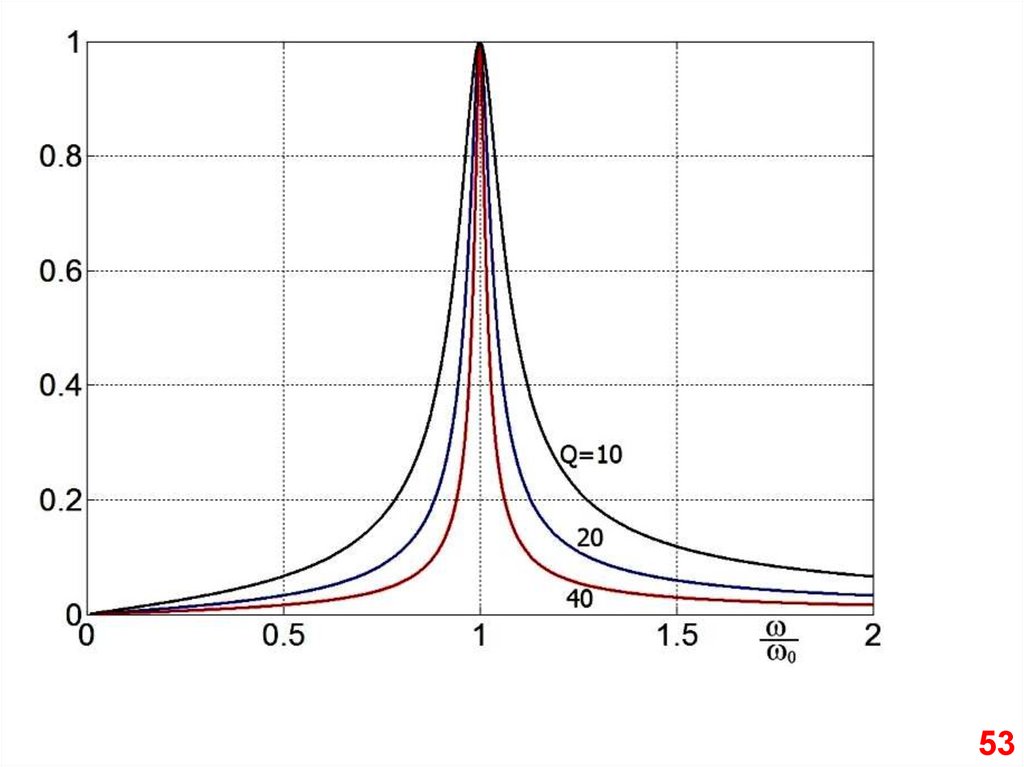
“Ширина” резонансной кривой49
50.
5051.
5152.
5253.
5354.
p.t.o.54
55.
5556.
5657.
5758.
5859.
5960.
6061.
The END61



















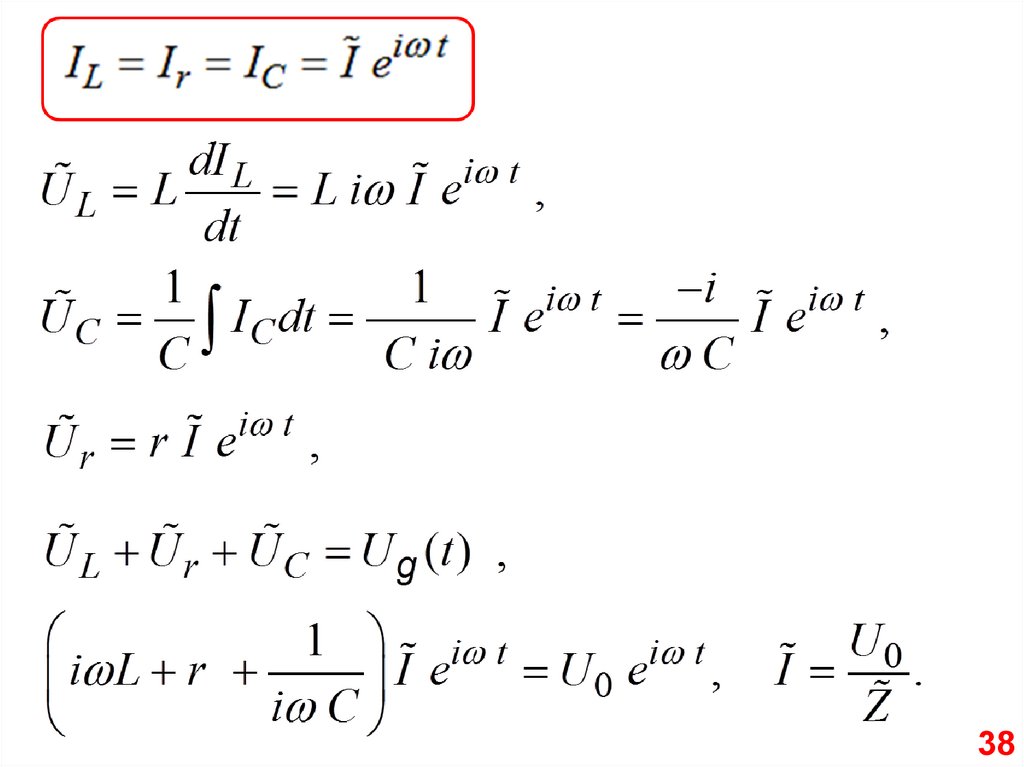













 physics
physics electronics
electronics








