Similar presentations:
Множини та операції над ними
1. Множини та операції над ними
12.
Роман Сікорський – польськийматематик, академік польської АН.
Основні роботи присвячені теорії
булевої алгебри – одному з розділів
сучасної математики.
“ Світ математичних понять дуже
різноманітний, ускладнений. Але всі
математичні поняття можна звести
до одного-єдиного…
Цим поняттям є множина. ”
Роман Сікорський
2
3.
Множина - це сукупність, зібрання деякихпредметів будь-якої природи.
множина букв
українського
алфавіту
множина цифр десяткової
нумерації
4.
Для позначення множин використовуютьсялітери латинського алфавіту або фігурні дужки:
множина А або {0, 1, 2, 3, 4, 5}.
Предмети, з яких складається множина, називаються
її елементами.
Дві множини називаються рівними, якщо вони
складаються з однакових елементів.
• Елемент а належить
множині М
а М
• Елемент b не належить
множині М
b
М
4
• У множині немає
елементів
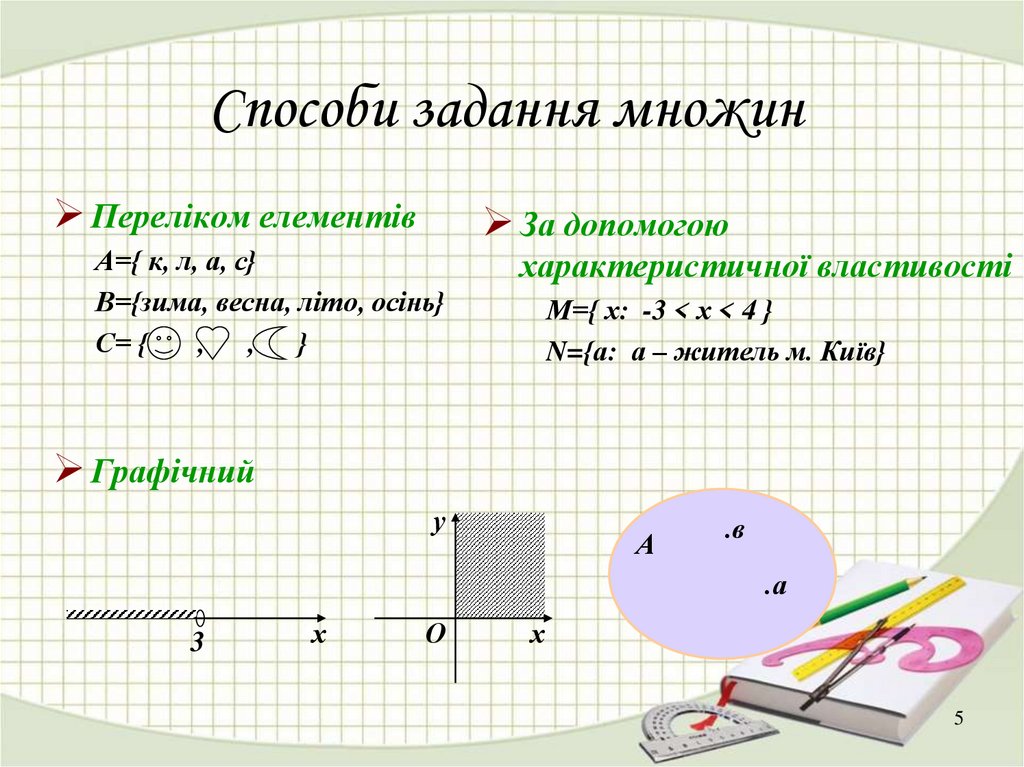
5. Способи задання множин
Переліком елементівЗа допомогою
А={ к, л, а, с}
В={зима, весна, літо, осінь}
С= {
, , }
характеристичної властивості
М={ х: -3 < х < 4 }
N={а: а – житель м. Київ}
Графічний
у
А
.в
.а
3
х
О
х
5
6. Множина A називається підмножиною множини B, якщо кожний елемент множини A є елементом множини B. А В
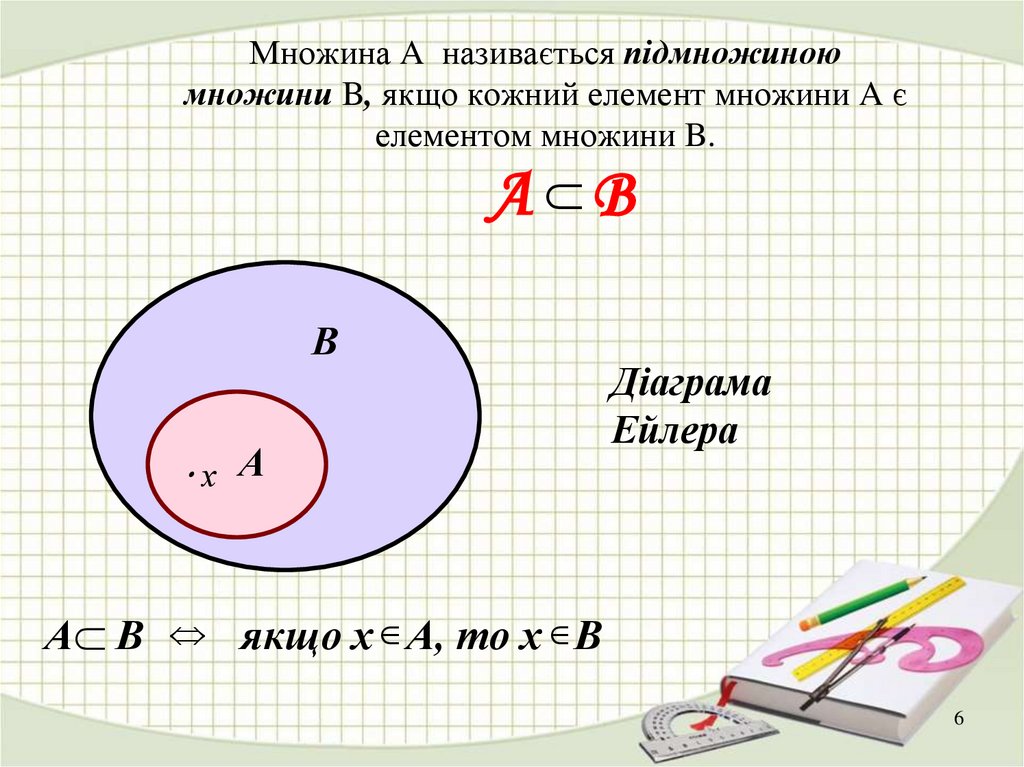
Множина A називається підмножиноюмножини B, якщо кожний елемент множини A є
елементом множини B.
А В
В
х А
Діаграма
Ейлера
А В якщо х А, то х В
6
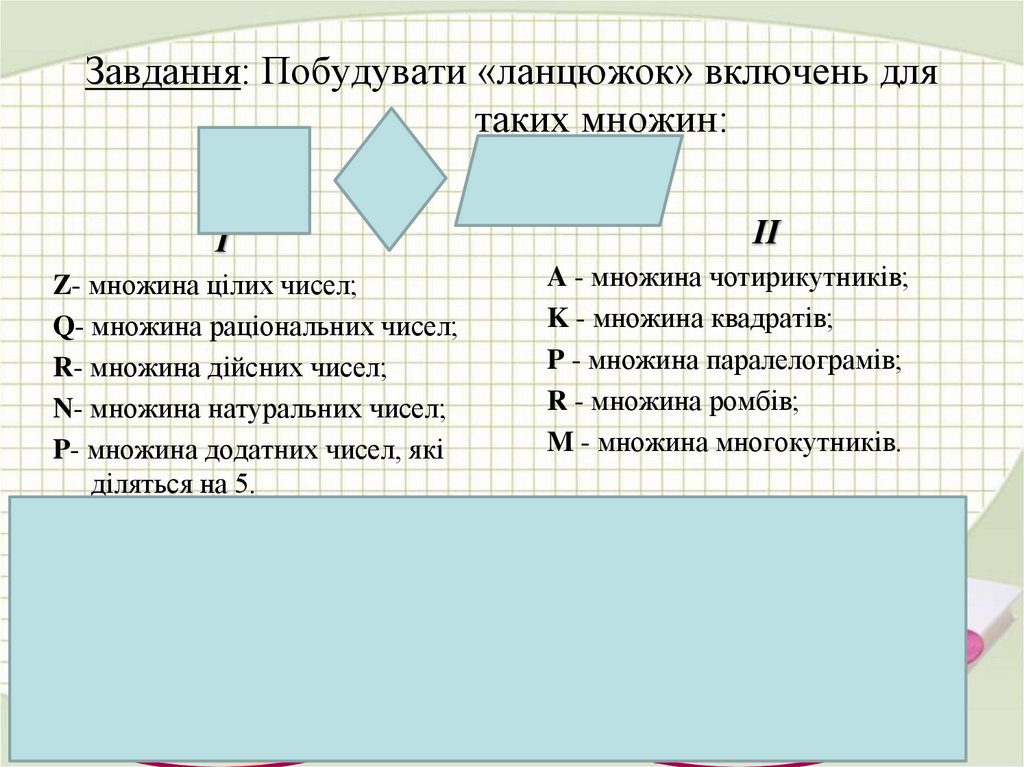
7. Завдання: Побудувати «ланцюжок» включень для таких множин:
ІІІ
Z- множина цілих чисел;
Q- множина раціональних чисел;
R- множина дійсних чисел;
N- множина натуральних чисел;
P- множина додатних чисел, які
діляться на 5.
P N Z Q R
P
N
Z
Q
R
A - множина чотирикутників;
K - множина квадратів;
P - множина паралелограмів;
R - множина ромбів;
M - множина многокутників.
K R P A M
K
R
P
A
M
7
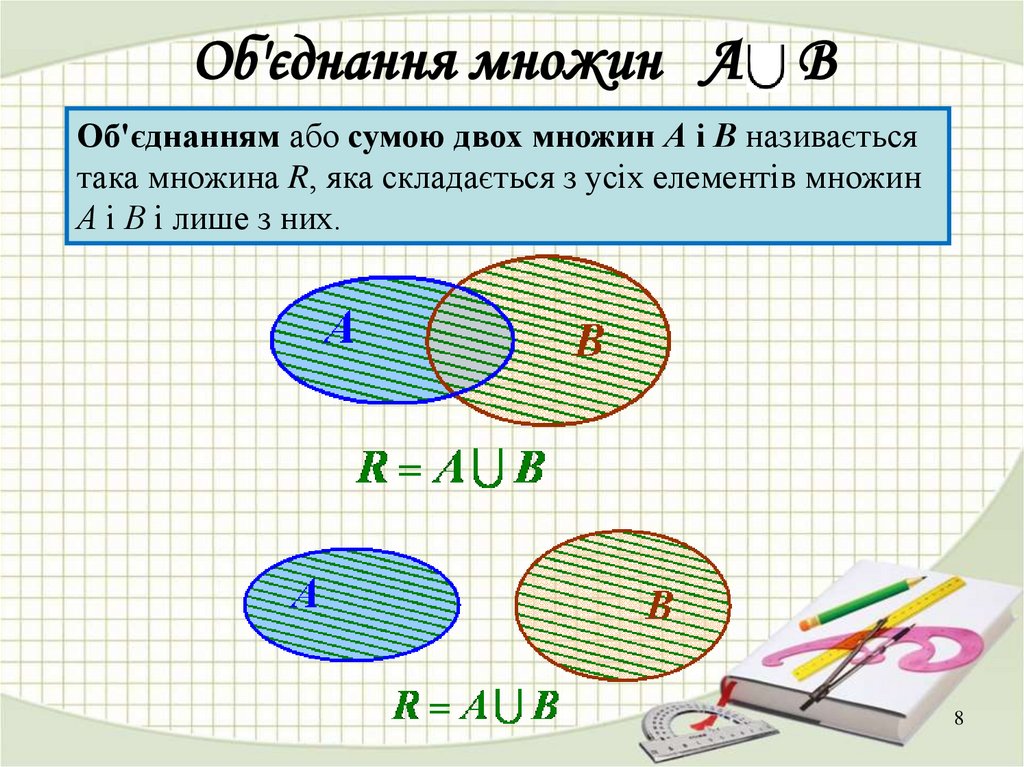
8. Об'єднання множин А В
Об'єднанням або сумою двох множин А і В називаєтьсятака множина R, яка складається з усіх елементів множин
А і В і лише з них.
8
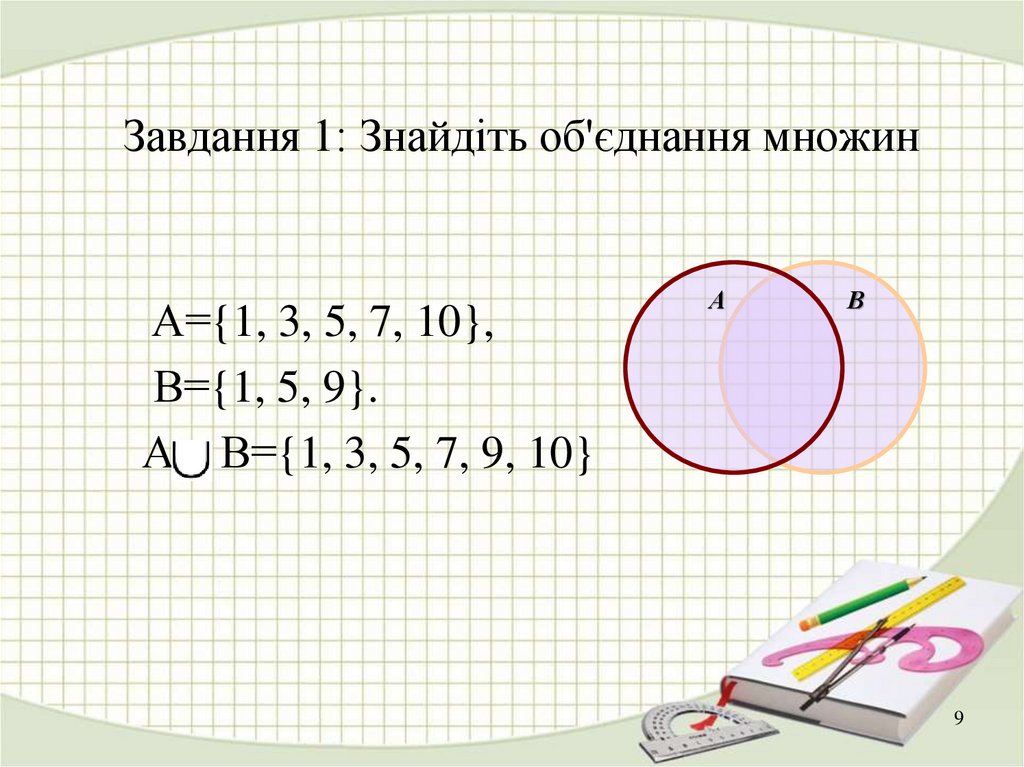
9. Завдання 1: Знайдіть об'єднання множин
А={1, 3, 5, 7, 10},В={1, 5, 9}.
А В={1, 3, 5, 7, 9, 10}
А
В
9
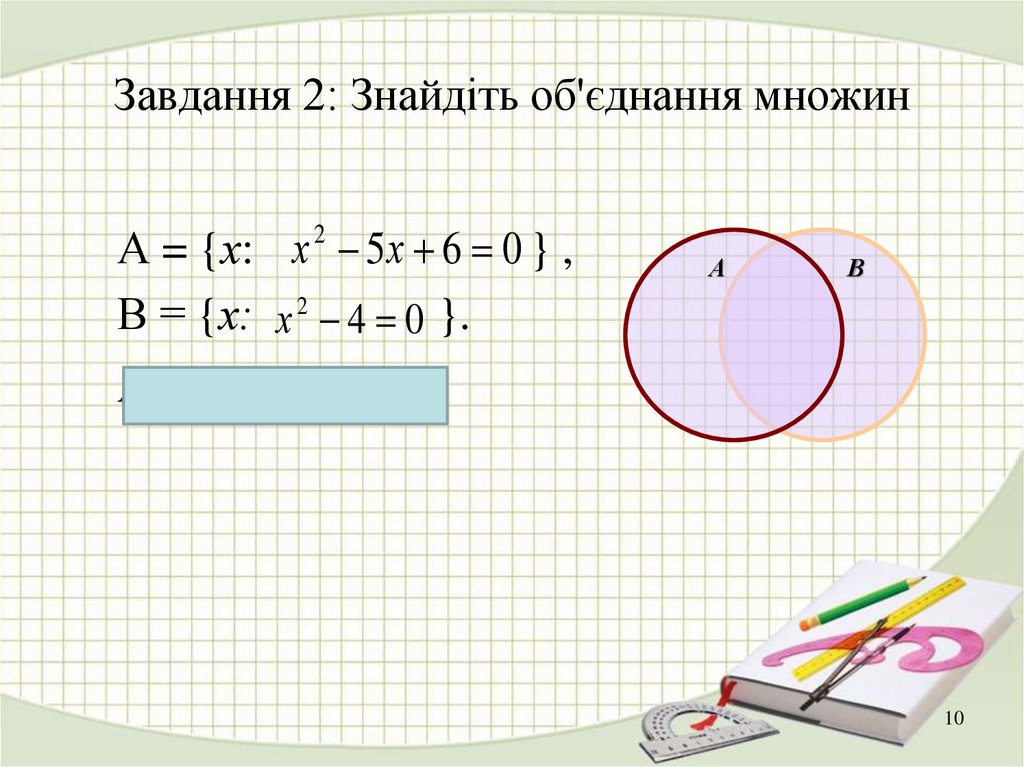
10. Завдання 2: Знайдіть об'єднання множин
А = {х: х 5 х 6 0 } ,В = {х: х 2 4 0 }.
2
А
А
В
В={-2; 2; 3}
10
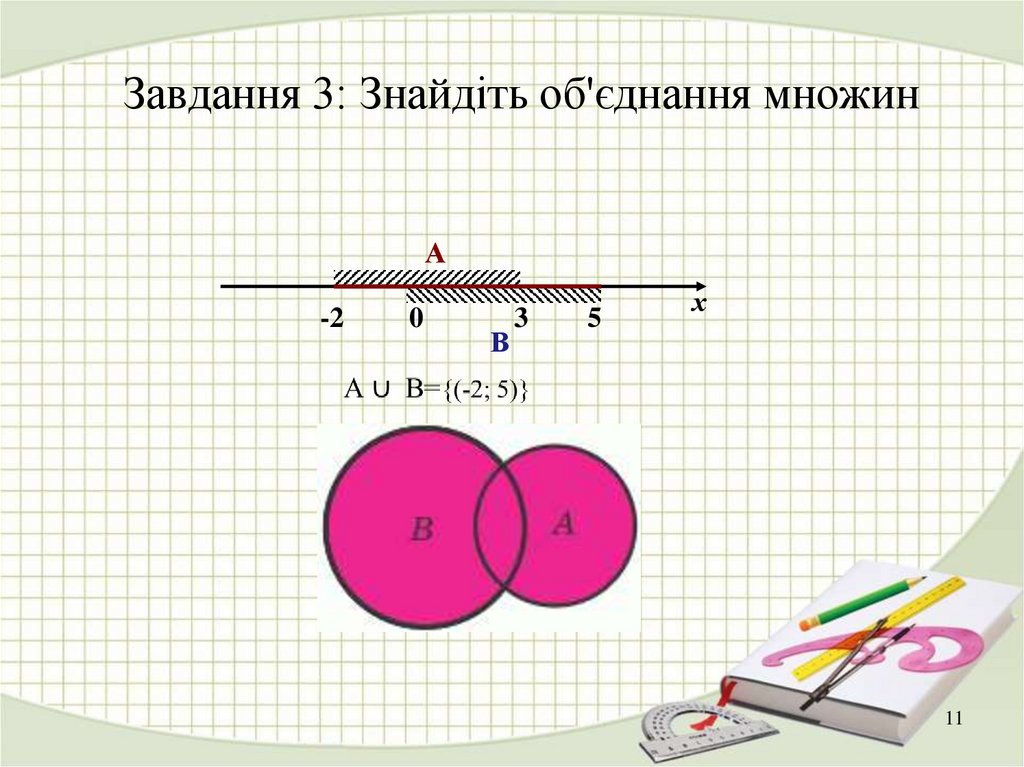
11. Завдання 3: Знайдіть об'єднання множин
А-2
0
В
3
5
х
11
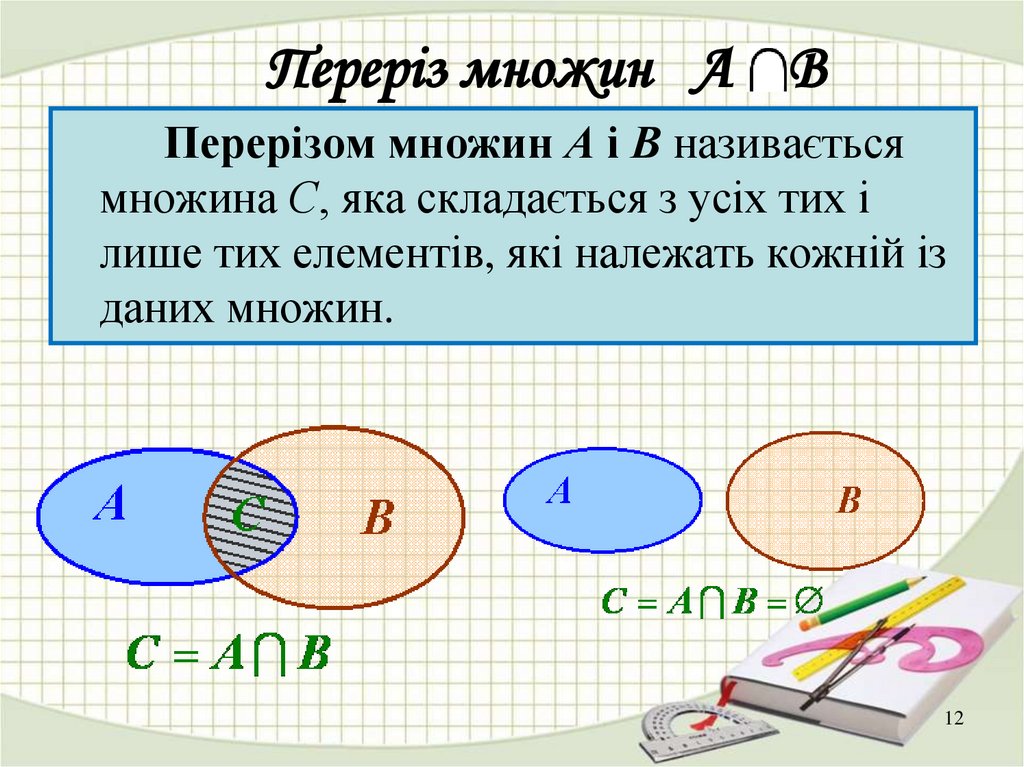
12. Переpіз множин А В
Перерізом множин А і В називаєтьсямножина С, яка складається з усіх тих і
лише тих елементів, які належать кожній із
даних множин.
12
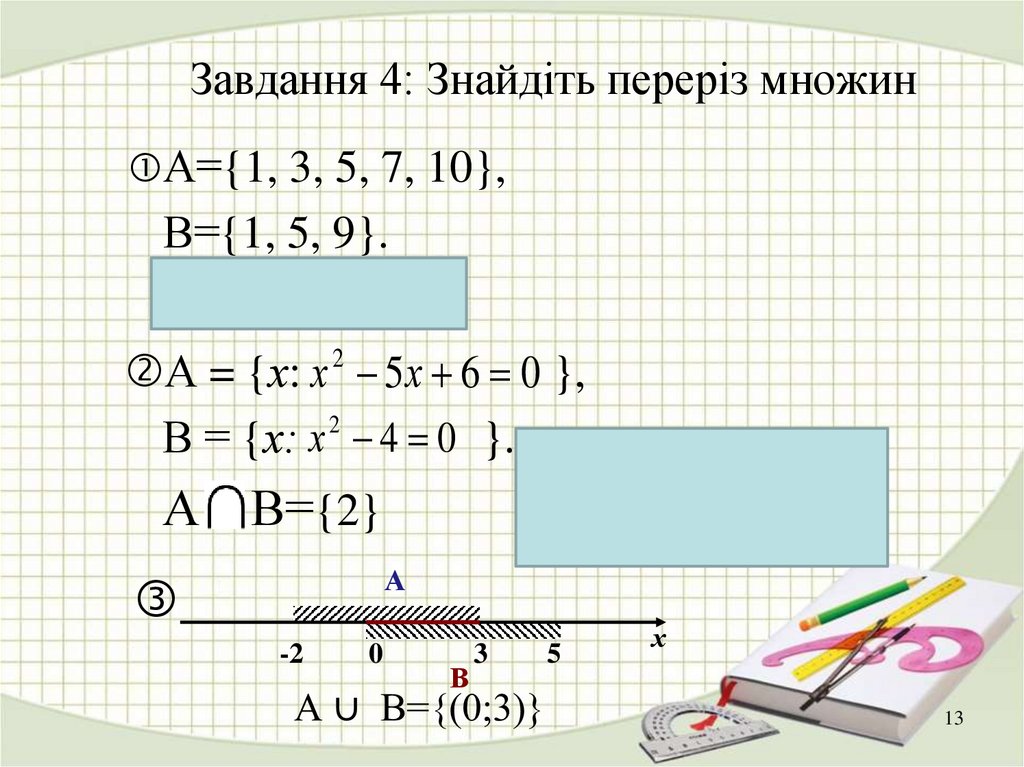
13. Завдання 4: Знайдіть переріз множин
А={1, 3, 5, 7, 10},В={1, 5, 9}.
А В={1, 5}
А = {х: х 5 х 6 0 },
В = {х: х 2 4 0 }.
2
А
В={2}
А
-2
0
В
3
5
х
13
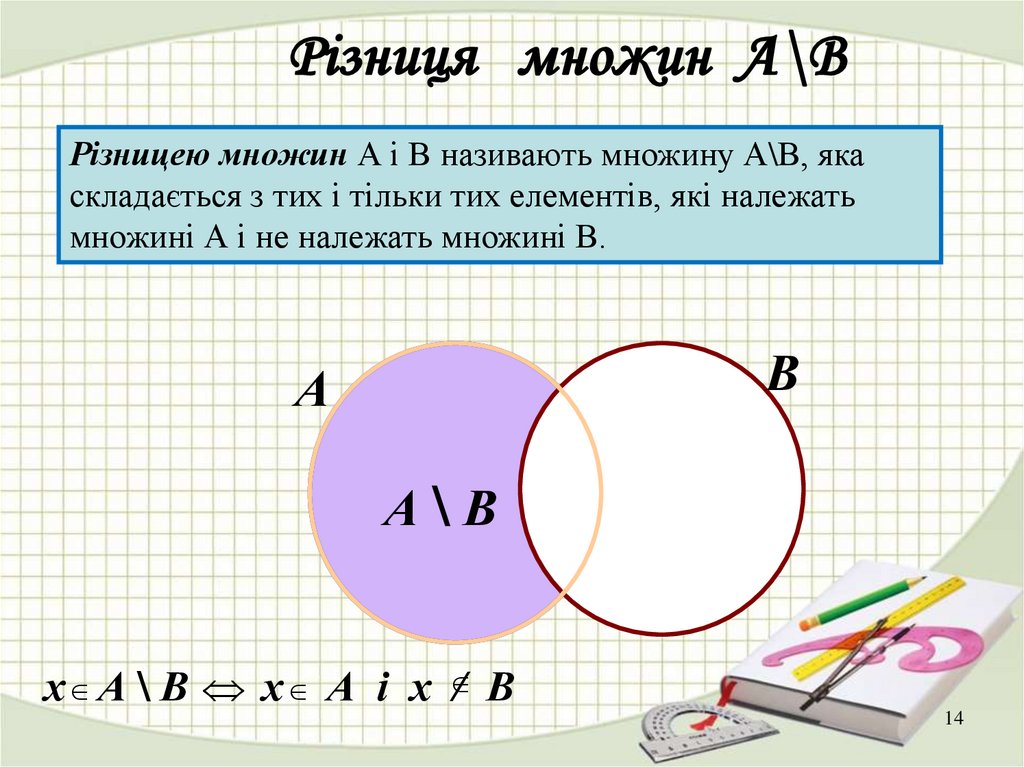
14. Різниця множин А\В
Різницею множин А і В називають множину А\В, якаскладається з тих і тільки тих елементів, які належать
множині А і не належать множині В.
В
А
А\В
х А \ В х А і х / В
14
15. Завдання 5: Знайдіть різниці множин
А={1, 3, 5, 7, 10},В={1, 5, 9}.
А \ В={3, 7, 10},
В \ А={ 9 }.
А = {х: х 2 5 х 6 0 } ,
В = {х: х 2 4 0 }.
А \ В={3},
В \ А={-2}
15
16.
Завдання 6. Знайдіть перетин, об'єднання ірізницю множин K i L,
якщо K = {1, 2, 3, 4, 5, 6, 7}, L = {2, 4, 6}.
Варіанти відповідей:
1. {1, 2, 3, 4, 5, 6, 7}
2. {2, 4, 6}
3. {1, 3, 5, 7}
4. порожня множина
5. {1, 2, 2, 3, 4, 4, 5, 6, 6, 7}






 mathematics
mathematics








