Similar presentations:
Регулярні множини. (Тема 3)
1. Тема 3: Регулярні множини
• 1. Регулярні множини і регулярні вирази• 2. Побудова регулярного виразу по
праволінійній граматиці
• 3. Алгоритм побудови праволінійної
граматики по регулярному виразу
2. 1. Регулярні множини і регулярні вирази
Нехай V - скінченний алфавіт. Рекурсивно регулярнамножина в алфавіті визначається так:
1) –регулярна множина в алфавіті V;
2) {e} –регулярна множина в алфавіті V;
3) {a}–регулярна множина в алфавіті V
для всіх a є V;
4) якщо – P,Q регулярні множини в V, то
P U Q, PQ, P*– регулярні множини в
алфавіті V ;
5) Ніщо інше не є регулярною множиною в V.
3. Регулярний вираз в алфавіті V визначається рекурсивно:
• 1) - регулярний вираз, що позначає регулярну множину ;• 2) e - регулярний вираз, що позначає регулярну множину {e};
• 3) якщо а V, то а - регулярний вираз, що позначає регулярну множину
{a};
• 4) якщо p,q - регулярні вирази, що позначають регулярні множини P,Q, то
(p+q) регулярний вираз, що позначає регулярну
множину P Q;
(pq) регулярний вираз, що позначає регулярну
– множину PQ;
(p)* регулярний вираз, що позначає регулярну
– множину P*;
• 5) ніщо інше не є регулярним виразом.
4. Приклади регулярних виразів.
1) 01 позначає множину {01};
2) 0* позначає множину {0}*;
3) (0+1)* позначає множину {0,1}*;
4) (0+1)*011 позначає множину усіх ланцюжків, що
складаються з нулів і одиниць і закінчуються
ланцюжком 011;
5)
(a+b)(a+b+0+1)* позначає множину усіх
ланцюжків з множини {a,b,0,1}*, що починаються з
а або b;
6) (11+00)*(01+10)(11+00)*
5. Тотожності над регулярними виразами
1)2)
3)
4)
5)
6)
( ) ( )
( )
e e
* *
7) * e
8) ( ) ( )
9) ( )
10) = =
11)
( * ) * *
12)
=
Доведення. 1) Нехай , позначають множини A, B.
Тоді + позначає A B,
+ позначає B A.
Оскільки A B =B A, то + = + .
6. 2. Побудова регулярного виразу по праволінійній граматиці
Рівняння з регулярнимикоефіцієнтами:
X= X+ ,
(1)
, – регулярні вирази.
X= *
(2)
– розв’язок (1)
При =e
* = * +
(3)
X= *( + ) - також розв’язок (1), оскільки + =(6) + + .
X= * - найменша нерухома точка рівняння (1).
7.
Стандартна система лінійних рівняньрегулярними коефіцієнтами має вигляд:
з
X 1 11 X 1 12 X 2 1n X n 1
X X X X
2
21 1
22 2
2n n
2
. . . . . . . . . . . . . . . . . . . . . . .
X n n1 X 1 n 2 X 2 nn X n n
ij i — регулярні вирази, X i — змінні (i,j=1,2,…,n).
11
X 1 11 X 1
12 X 2 ... 1n X n 1
X 1 ( 11 ) *
8. X= X+ X= *
G ({S , A, B}, {0,1}, P, S )P:
S 0 A | 1S | e
A 0 B | 1A
B 0 S | 1B
X= X+
X= *
x1 1 x1 0 x2 e
x1 1* (0 x2 e)
x2 1 0 x3
*
x3 01* (0 x2 e) 1x3
S x1 , A x 2 , B x3
x1 0 x 2 1x1 e
x 2 0 x3 1x 2
x 0 x 1x
1
3
3
x3 01*0 x2 01* 1x3
01*01*0 x3 01* 1x3
*
(01*01*0 1* ) x3 01
x3 (01*01*0 1)* 01*
x2 1*0(01*01*0 1)* 01*
x1 1* (01*0(01*01*0 1)* 01* e)
9. Завдання додому: Розв’язати систему рівнянь із регулярними коефіцієнтами:
G=({S,A,B},{0,1}, P, S)l=1*(01*0(01*01*+1)*01*+e)
Завдання додому:
Розв’язати систему рівнянь із
регулярними коефіцієнтами:
A1 (01 1) A1 A2
A2 11 1A1 00 A3
A e A A
1
2
3
*
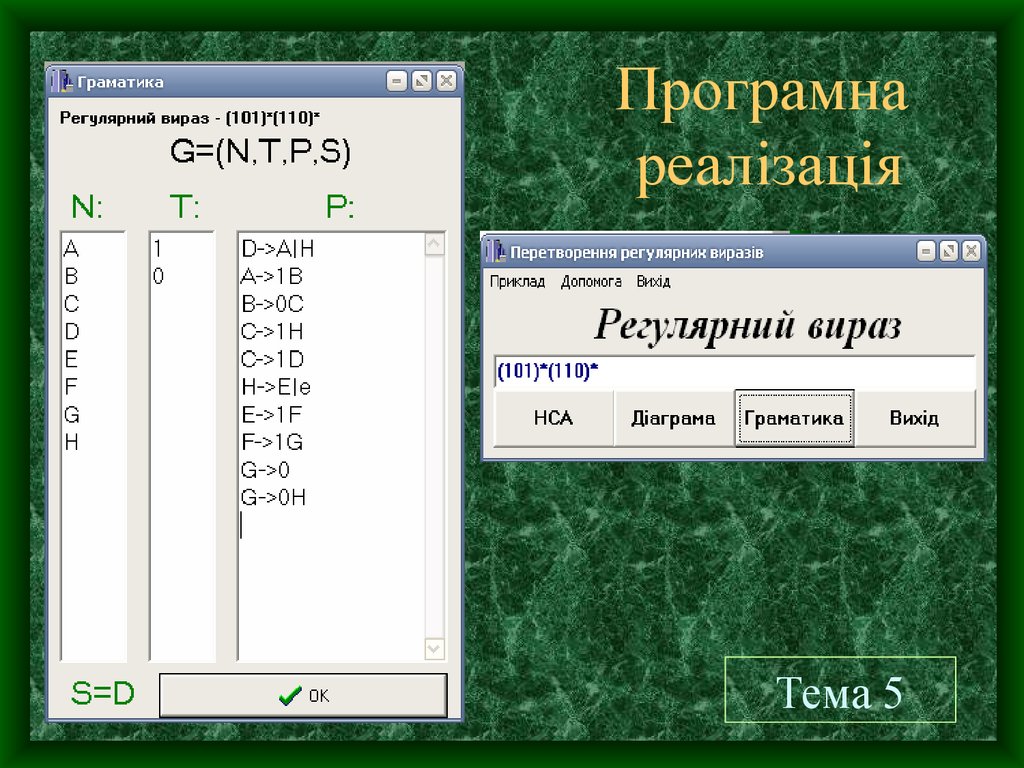
10.
Програмнареалізація
11. 3. Алгоритм побудови праволінійної граматики по регулярному виразу
1. Для регулярного виразу : G ({S}, T , , S )2. Для регулярного виразу e : G ({S}, T ,{S e}, S )
3. Для регулярного виразу a, a T : G ({S}, T ,{S a}, S )
Нехай ми маємо регулярні вирази
l1 :G1 ( N 1 , T , P1 , S1 )
l 2 :G2 ( N 2 , T , P2 , S 2 )
N 1 N 2 .
4. Для l1 l 2 : G3 ( N 1 N 2 S 3 , T , P1 P2 {S 3 S1 | S 2 }, S 3 )
5. Для l1l 2 : G4 ( N 1 N 2 , T , P4 , S1 )
P4 :
а) якщо A xB P1 , то це правило належить P4
б) якщо A x P1 , тоді A xS 2 P4
в) всі правила з P2 належать P4.
12.
6. Для (l1 ) * : G5 ( N1 S 5 , T , P5 , S 5 )P5 :
а) якщо A xB P1 , то це правило належить
A x
P5
б) якщо A x P1 , то
A xS 5
в) S 5 S1 | e належить P5
Приклад 2. l=(101)*(010)*
P5 :
l1 101
l 2 010
P1 : S1 101
P2 : S 2 010
l3 (101)
l 4 (010)
*
*
P3 :
P4 :
S 3 S1 | e
S4 S2 | e
S1 101
S2 010
S1 101S 3
S2 010S4
S3 S1 | S4
S1 101S4
S1 101S3
S4 S2 | e
S2 010
S2 010S4
P5
13.
P5 :S3 S1 | S4
S1 101S4
S3 S
S1 A
S1 101S3
S2 B
S4 S2 | e
S4 C
S2 010
S2 010S4
l=(101)*(010)*
P5 P
P:
S A|C
A 101C | 101S
C B |e
B 010 | 010C
G=({S,A,B,C},{0,1}, P, S)
Завдання додому: Для регулярного
виразу
l=(01)*(0+1)
побудувати
праволінійну граматику.













 mathematics
mathematics








