Similar presentations:
Формулы сокращенного умножения
1.
Формулы сокращенного умножения1. a b a b a b .
2
2
2. a b a b a b
2
a 2 ab b .
2
2
3. a b a b a b
2
a 2 ab b .
2
2
2.
Формулы сокращённого умножения1) Квадрат суммы двух выражений
1) a b a 2ab b
2
2
2
2) Квадрат разности двух выражений
2) a b a 2ab b
2
2
2
Разложение на множители (обратные формулы)
1) a 2ab b a b
2
2
2
2) a 2ab b a b
3) Разность квадратов двух выражений
2
2
a b ( a b) ( a b)
2
2
2
3.
Формулы сокращённого умноженияСумма кубов двух выражений
a b (a b) (a ab b )
3
3
2
2
Разность кубов двух выражений
a b (a b) (a ab b )
3
3
2
2
Куб суммы двух выражений
a b
3
a 3a b 3ab b
3
2
2
3
Куб разности двух выражений
a b
3
a 3a b 3ab b
3
2
2
3
4.
№1 .Преобразуйт е в многочлен(5b 4 x) 5b 4 x
2
2
(5b) (4 x)
2
2
25b 16 x .
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
5.
№2. Преобразуйт е в многочлен(3 y 5) 3 y 5
(3 y ) (5)
2
2
9 y 25.
2
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
6.
№3. Преобразуйт е в многочлен(a 3)
2
a 2 a 3 3
2
2
a 6 a 9.
2
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
7.
№4. Преобразуйт е в многочлен(x 4)
2
2
x 2 x 4 4
2
x 8 x 16.
2
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
8.
№5. Преобразуйт е в многочлен(2 x y )
2
2
(2 x) 2 2 x y y
2
4 x 4 xy y .
2
a b a b
2
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
9.
№6. Разложит е на множит ели.
25b 16 x
2
2
(5b) (4 x)
(5b 4 x) 5b 4 x .
2
a b a b
2
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
10.
№7. Разложит е на множит ели.
9 y 25
2
(3 y ) (5)
2
2
(3 y 5) 3 y 5 .
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
11.
№8. Разложит е на множит ели.
a 6a 9
2
a 2 a 3 3
2
2
(a 3) .
2
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
12.
№9. Разложит е на множит ели.4 x 4 xy y
2
2
(2 x) 2 2 x y y
2
2
(2 x y ) .
2
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
13.
№10. Упрост ит ь выражения.1) c 2 c 3 с 1
2
2
с 2с 3с 6 (с 2с 1)
2
2
с с 6 с 2с 1 3с 7.
2
2)3 a с 6ac
2
2
3 a 2ac с 6ac
2
3a 6ac 3c 6ac
2
2
2
2
3a 3c 3(a c ).
2
a b a b
2
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
14.
№1.Разложит е на множит ели.8 a 2 a
2
2
( 2 a ) ( 2 2a a )
3
3
3
(2 a ) (4 2a a ).
2
=
(
_
+
(
+
_
3
(
2
_
+
+
2
(
3
15.
№2.Разложит е на множит ели.x y (x ) ( y )
12
9
4 3
3 3
( x y ) (( x ) x y ( y ) )
4
3
4 2
4 3
3 2
( x y ) ( x x y y ).
+
_
3
=
(
8
_
+
4 3
(
3
3
(
2
_
+
6
+
2
(
4
16.
№3.Разложит е на множит ели.b 27a b (3a )
3
3
3
3
(b 3a) (b 3ab (3a) )
2
2
(b 3a) (b 3ab 9a ).
+
_
3
=
(
_
+
(
3
(
2
2
_
+
+
2
(
2
17.
№4.Разложит е на множит ели.64c a b (4c ) (ab)
6
3 3
2 3
3
(4c ab) (( 4c ) 4c ab (ab) )
2
2 2
2
(4c ab) (16c 4abc a b ).
+
_
3
=
(
_
+
(
3
4
(
2 2
2
_
+
+
2
(
2
18.
№5 .Преобразуйт е в многочленa) x y x xy y
2
2
x y .
3
3
б ) x 2 y x 2 xy 4 y
2
2
x (2 y ) x 8 y .
+
_
3
=
(
_
+
3
(
3
3
(
2
_
+
3
+
2
(
3
19.
№6 .Преобразуйт е в многочленa) x y x xy y
2
2
x y .
3
3
б ) x 2 y x 2 xy 4 y
2
2
x (2 y ) x 8 y .
+
_
3
=
(
_
+
3
(
3
3
(
2
_
+
3
+
2
(
3
20.
Уст ноПредст авит ь в виде удвоенного произведения:
16
2
9x
25a
2
0,64в
4
y
4
x y
2
0,25а
50 x
2
3т
0,5 p
ав
2
6
21.
Уст ноПредст авит ь в виде квадрат а одночлена:
4a
2
9x
0,25 x y
4
0,64а
4 2
0,01a b
2
2
25a
2
0,04 x
1 2 2
ab
9
4
6
9 2 4
x y
16
9 4 6
1 m n
16
22.
Уст ноПредст авит ь в виде куба одночлена:
ab
6 9
x y
3 6
8m n
9 27
125k b
3 3
0,064а b
3 9
0,008 р q
12 15
1 9
p
64
27 18
p
125
125 24
a
216
23.
Уст ноРазложит ь на множит ели:
a 8
3
b 27
3
216 m
3
64a 1
3
a b 1
1 3 8 3
a b
8
27
3 3
24.
Уст ноРазложит ь на множит ели:
a 8
9
27 b
3 3
3
x y c
3
3 9
a m n
1 6 9
a b
8
6
(2с 1) 64
3
25.
Самостоятельная работа №11 вариант
2 вариант
№1.Упростить выражение
1)(b 3) b 3 ;
2)( 2c 1) 2c 1 ;
3)( x 3 y ) x 3 y ;
4)(10a b) b 10a ;
1)( a 2) a 2 ;
2)(3b 1) 3b 1 ;
3)( a 2b) a 2b ;
4)( 4a b) b 4a ;
№2.Разложите на множители:
1)9 p 2 4; 4)36 x 2 25 y 2 ;
1
2) c 2 ; 5)a 2b 2 9;
36
3)4 x 2 y 2 ; 6) a 4 81;
1)4 x 2 1;
4)49 x 121a ;
2 2
2
2
5
)
x
y 1;
2)m a ;
4
2
2
6
)
a
16;
3)a 9 y ;
2
2
26.
Проверим №1:1 вариант
1)(b 3) b 3 b 2 9
2)( 2c 1) 2c 1 4c 2 1
3)( x 3 y ) x 3 y x 2 9 y 2
4)(10a b) b 10a 100a 2 b 2
2 вариант
1)( a 2) a 2 a 2 4
2)(3b 1) 3b 1 9b 2 2 1
2
a
4b
3)( a 2b) a 2b
4)( 4a b) b 4a 16a 2 b 2
2
_
2
=(
_
) (
+
)
27.
Проверим №2 (1 вариант)1)9 p 2 4 3 p 2 3 p 2
1
2) c 2 1 c 1 c
36
6
6
3)4 x 2 y 2 2 x y 2 x y
4)36 x 2 25 y 2 6 x 5 y 6 x 5 y
5)a 2b 2 9 ab 3 ab 3
6) a 4 81 9 а 2 9 а 2
2
_
2
=(
_
) (
+
)
28.
Проверим №2 (2 вариант)1)4 x 2 1 2 x 1 2 x 1
2)m 2 a 2 m a m a
3)а 2 9 y 2 a 3 y a 3 y
4)49 x 2 121a 2 7 x 11a 7 x 11a
5) x 2 y 2 1 xy 1 xy 1
6) a 4 16 4 а 2 4 а 2
2
_
2
=(
_
) (
+
)
29.
Самостоятельная работа №21 вариант
2 вариант
Разложить на множители
1)(3 x 1) 4 x 3
1)( 2a 7b) 3a 5b
2
2
2
2
2)( a b c) a b c 2)( x y a)2 x y a 2
2
2
3)9b a 3b
2
2
3)81x 9 x 7 y
2
2
30.
ПРОВЕРИМ!1 вариант
1)(3 x 1) 4 x 3
(3 x 1 4 x 3)(3 x 1 4 x 3) ( x 2)(7 x 4)
( x 2)(7 x 4).
2
2
2)( a b c) a b c
(a b c a b c) (a b c a b c)
(2b 2c) 2a 4a (b c).
2
2
3)9b a 3b (3b) 2 a 3b 2
2
2
(3b) a 3b (3b a 3b) (3b a 3b)
a (6b a ).
2
2
2
_
2
=(
_
) (
+
)
31.
ПРОВЕРИМ!2 вариант
1)( 2a 7b) 3a 5b ( 2a 7b 3a 5b)
( 2a 7b 3a 5b) (12b a ) (5a 2b).
2
2
2)( x y a )
2
2
x y a ( x y a x y a)
( x y a x y a ) 2 y ( 2 x 2a ) 4 y ( x a ).
3)81x 9 x 7 y (9 x) 9 x 7 y
2
2
2
2
(9 x 9 x 7 y ) (9 x 9 x 7 y ) ( 7 y ) (18 x 7 y )
7 y (7 y 18 x ).
2
_
2
=(
_
) (
+
)
32.
Самостоятельная работа №31 вариант
2 вариант
№1.Выполните преобразование:
1)(9 a ) ;
2
2)(8 b) 2 ;
3)(3 y 4) 2 ;
4)(5a 6b) 2 ;
1)( 2 y )3 ;
2)(6 c) 2 ;
3)( 2 x 9) 2 ;
4)(7m 3n) 2 ;
№2.Выполните действия:
1)(( a b) c) 2 ;
2
2)(( a b) c) ;
3)( x y z ) 2 ;
1)( a (b c)) 2 ;
2
2)( a (b c)) ;
3)( x y z ) 2 ;
4)( x y z )( x y z ).
4)( x y z )( x y z ).
33.
Проверим №1:1 вариант
1)(9 a ) 2 9 2 2 9 a a 2 81 18a a 2 .
2)(8 b) 2 82 2 8 b b 2 64 16b b 2 .
3)(3 y 4) 2 (3 y ) 2 2 3 y 4 42 9 y 2 24 y 16.
4)(5a 6b) 2 (5a) 2 2 5a 6b (6b) 2 25a 2 60ab 36b 2 .
2 вариант
1)( 2 y ) 2 23 2 2 y y 3 8 4 y y 3 .
2)(6 c) 2 6 2 2 6 c с 2 36 12c с 2 .
3)( 2 x 9) 2 (2 x) 2 2 2 x 9 92 4 x 2 36 x 81.
4)(7 m 3n) 2 (7m) 2 2 7 m 3n (3n) 2 49m 2 42mn 9n 2 .
(
(
_
+
2
=
2
_
+
2
+
2
34.
Проверим №2 (1 вариант)1)(( a b) c) 2 (a b) 2 2 (a b) c c 2
a 2 2ab b 2 2ac 2bc c 2
a 2 b 2 с 2 2ab 2ac 2bc.
2)(( a b) c) 2 (a b) 2 2(a b)c c 2
a 2 2ab b 2 2ac 2bc c 2
a 2 b 2 c 2 2ab 2ac 2bc.
3)( x y z ) 2
4)( x y z )( x y z )
(
(
_
+
2
=
2
_
+
2
+
2
35.
Проверим №2 (2 вариант)1)( a (b c)) 2 a 2 2a(b c) (b c) 2
a 2 2ab 2ac b 2 2bc c 2
a 2 b 2 c 2 2ab 2ac 2bc.
2)( a (b c)) 2 a 2 2a (b c) (b c) 2
a 2 2ab 2ac b 2 2bc c 2
2
2
2
a b c 2ab 2ac 2bc.
3)( x y z ) 2 ;
4)( x y z )( x y z ).
(
(
_
+
2
=
2
_
+
2
+
2
36.
Учебник Алимова Ш.А. и др.№352
Разложить на множители.
№352
№353
№356
№357
№359
№360
1)25 x 9
2
нечётные
3)64 y 36 x
2
2
2
_
2
=(
_
) (
+
)
37.
Учебник Алимова Ш.А. и др.№353
Разложить на множители.
№352
№353
№356
№357
№359
№360
1 2 16 2
1) y x
9
25
нечётные
3)0,25a 0,49b
2
2
_
2
2
=(
_
) (
+
)
38.
Учебник Алимова Ш.А. и др.№356
Выполнить умножение.
№352
№353
№356
№357
№359
№360
1)( 2b a )( 2b a )
нечётные
3)( y 6 x )( y 6 x )
2
_
2
=(
_
) (
+
)
39.
Учебник Алимова Ш.А. и др.№357
Выполнить умножение.
№352
№353
№356
№357
№359
№360
1)(с d )(c d )
2
2
2
2
нечётные
3)( x y )( y x )
4
3
2
_
3
2
=(
4
_
) (
+
)
40.
Учебник Алимова Ш.А. и др.№359
Вычислить.
№352
№353
№356
№357
№359
№360
1) 48·52=
нечётные
3) 43·37=
2
_
2
=(
_
) (
+
)
41.
Учебник Алимова Ш.А. и др.№359
Вычислить.
№352
№353
№356
№357
№359
№360
1)47·33=
нечётные
3)84·76=
2
_
2
=(
_
) (
+
)
42.
Учебник Алимова Ш.А. и др.№354
Разложить на множители.
№354
№355
№358
№361
№362
1)36 x y 1
2
2
нечётные
3) x y 16
2
2
_
4
2
=(
_
) (
+
)
43.
Учебник Алимова Ш.А. и др.№355
Разложить на множители.
№354
№355
1)a b
4
4
№358
№361
№362
нечётные
3)a 16
4
2
_
2
=(
_
) (
+
)
44.
Учебник Алимова Ш.А. и др.№358
Выполнить умножение.
№354
1)(3a 4b ) (3a 4b )
2
3
2
3
№355
№358
№361
№362
нечётные
3)(0,2m3 0,5 p 4 ) (0,5 p 4 0,2m3 )
2
_
2
=(
_
) (
+
)
45.
Учебник Алимова Ш.А. и др.№361
Разложить на множители.
№354
1)( a b) c
2
2
№355
№358
№361
№362
нечётные
3)( a 2b) 9a
2
_
2
2
2
=(
_
) (
+
)
46.
Учебник Алимова Ш.А. и др.№362
Разложить на множители.
№354
№355
1)( a b) (a c)
2
2
№358
№361
№362
нечётные
3)( 2a b) (2b a)
2
2
_
2
=(
2
_
) (
+
)
47.
Учебник Алимова Ш.А. и др.№363(1,3,5)
Вычислить:
№363
№364
№365
№366
№367
№368
1)47 2 37 2
3)50,7 2 50,62
2
нечётные
2
2 1
5) 6 5
3 3
2
_
2
=(
_
) (
+
)
48.
Учебник Алимова Ш.А. и др.№364(1,3)
Решить уравнения:
1)( x 1) x 1 x 2 2 x 3 ;
№363
№364
№365
№366
№367
№368
нечётные
3)( 2 x 3) 2 x 3 4 x 1 x 1 49;
2
_
2
=(
_
) (
+
)
49.
Учебник Алимова Ш.А. и др.№365(1,3)
Выполнить умножение:
1)(3 x) 3 x 9 x
2
№363
№364
№365
№366
№367
№368
3)( x 1) x 1 x 1
2
2
_
2
=(
_
нечётные
) (
+
)
50.
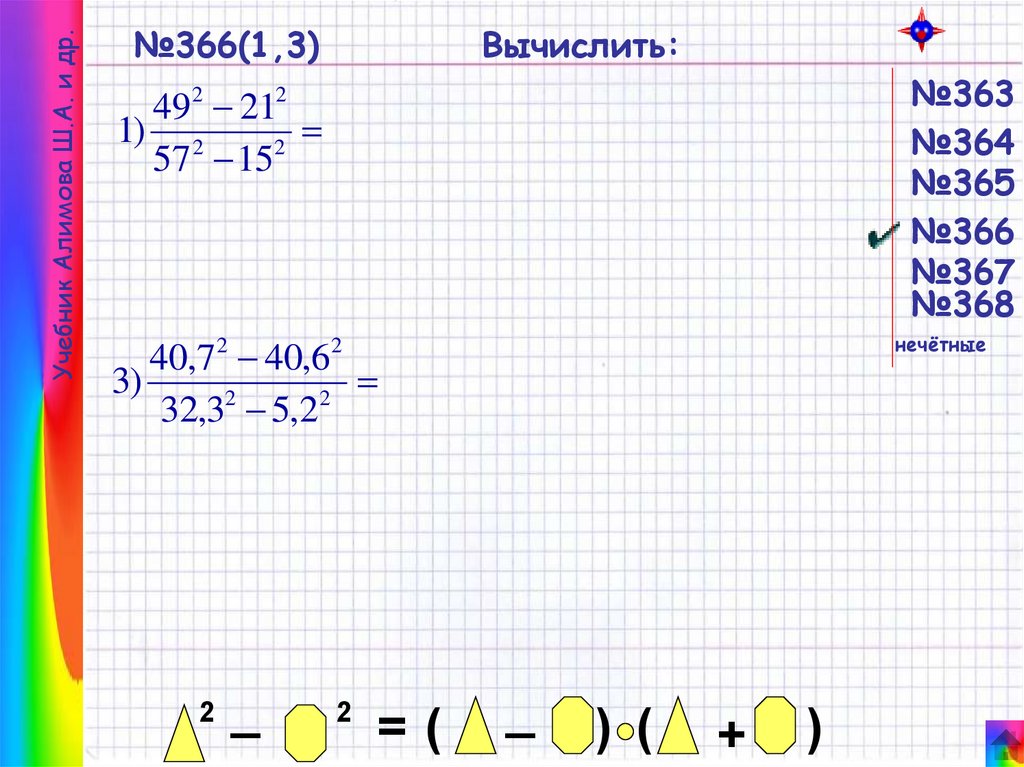
Учебник Алимова Ш.А. и др.№366(1,3)
Вычислить:
№363
№364
№365
№366
№367
№368
492 212
1) 2
2
57 15
нечётные
40,7 2 40,62
3)
2
2
32,3 5,2
2
_
2
=(
_
) (
+
)
51.
Учебник Алимова Ш.А. и др.№367
Доказать, что модуль разности квадратов
двух последовательных натуральных
чисел есть нечётное число.
№363
№364
№365
№366
№367
№368
нечётные
2
_
2
=(
_
) (
+
)
52.
Учебник Алимова Ш.А. и др.№368
Доказать, что при любом натуральном n
число (7n+1)²-(2n-4)² делится на 15.
№363
№364
№365
№366
№367
№368
нечётные
2
_
2
=(
_
) (
+
)
53.
№370(1,3)№371(1,3)
№372(1,3)
№373(1,3)
№374(1,3)
№375(1,3)
№376(1,3)
в виде многочлена
1) (с d )
2
3) (2 x)
2
(
_
+
(
Учебник Алимова Ш.А. и др.
№370(1,3)
Представить квадрат двучлена
2
=
2
_
+
2
+
2
54.
№370(1,3)№371(1,3)
№372(1,3)
№373(1,3)
№374(1,3)
№375(1,3)
№376(1,3)
в виде многочлена
1)( q 2 p )
2
3)(6a 4b)
2
(
_
+
(
Учебник Алимова Ш.А. и др.
№371(1,3)
Представить квадрат двучлена
2
=
2
_
+
2
+
2
55.
№370(1,3)№371(1,3)
№372(1,3)
№373(1,3)
№374(1,3)
№375(1,3)
№376(1,3)
в виде многочлена
1)(0,2 x 0,3 y )
2
2
2 3 3
3) x
4
3
(
_
+
(
Учебник Алимова Ш.А. и др.
№372(1,3)
Представить квадрат двучлена
2
=
2
_
+
2
+
2
56.
№370(1,3)№371(1,3)
№372(1,3)
№373(1,3)
№374(1,3)
№375(1,3)
№376(1,3)
в виде многочлена
1)( 4ав 5а )
2 2
3)(0,2 x 5 xy)
2
(
_
+
2
(
Учебник Алимова Ш.А. и др.
№373(1,3)
Представить квадрат двучлена
2
=
2
_
+
2
+
2
57.
№374(1,3)№370(1,3)
№371(1,3)
№372(1,3)
№373(1,3)
№374(1,3)
№375(1,3)
№376(1,3)
используя ФСУ
1)(90 1)
2
3)101
2
(
_
+
(
Учебник Алимова Ш.А. и др.
Выполнить действия,
2
=
2
_
+
2
+
2
58.
№370(1,3)№371(1,3)
№372(1,3)
№373(1,3)
№374(1,3)
№375(1,3)
№376(1,3)
используя ФСУ
1)72
2
3)997
2
(
_
+
(
Учебник Алимова Ш.А. и др.
№375(1,3)
Выполнить действия,
2
=
2
_
+
2
+
2
59.
№370(1,3)№371(1,3)
№372(1,3)
№373(1,3)
№374(1,3)
№375(1,3)
№376(неч.)
1)1,005
2
3)1,012
2
5)0,992
2
7)0,998
2
(
_
+
(
Учебник Алимова Ш.А. и др.
№376(неч.)
Применяя формулу (1+a)²≈1+2a,
найти приближённое значение числа.
2
=
2
_
+
2
+
2
60.
Разложит ь на множит ели:№383(2,4)
2) 9 6b b
2
№384(2,4)
№385(2,4)
№388(2,4)
№416(2,4)
4) 12ab 3a 12b
2
(
_
+
(
Учебник Алимова Ш.А. и др.
№383(2,4)
2
=
2
2
_
+
2
№417(2,4)
+
2
61.
Учебник Алимова Ш.А. и др.№384(2,4)
Решит ь уравнения:
2)64 x (3 8 x) 87
2
2
№383(2,4)
№384(2,4)
№385(2,4)
№388(2,4)
№416(2,4)
№417(2,4)
4)( 2 x 3) (2 x 3) 12
2
2
62.
Учебник Алимова Ш.А. и др.№385(2,4)
Упрост ит ь выражения:
2)( x y ) ( x y )
2
2
№383(2,4)
№384(2,4)
№385(2,4)
№388(2,4)
№416(2,4)
№417(2,4)
4)( 2a b) (2a b)
2
2
63.
Учебник Алимова Ш.А. и др.№388(2,4)
Вычислит ь:
2)37 126 37 63
2
2
№383(2,4)
№384(2,4)
№385(2,4)
№388(2,4)
№416(2,4)
№417(2,4)
85 17
4) 2
2
85 2 85 17 17
2
2
64.
Учебник Алимова Ш.А. и др.№416(2,4)
Упрост ит ь выражения:
2)(5 x ) (7 x )
2 2
2 2
№383(2,4)
№384(2,4)
№385(2,4)
№388(2,4)
№416(2,4)
4)(7 5 x) (3 x 2)
2
2
№417(2,4)
65.
Учебник Алимова Ш.А. и др.№417(2,4)
Решит ь уравнения:
2)( y 2)( y 3) ( y 2) 5
2
№383(2,4)
№384(2,4)
№385(2,4)
№388(2,4)
№416(2,4)
4)( y 8) ( y 9)( y 5) 117
2
№417(2,4)
66.
Учебник Алимова Ш.А. и др.№395(2,4)
2)1 ( x
2
Разложить на множители
№395(2,4)
2
2 xy y )
№396(2,4,6)
№397(2,4)
№398(2,4)
4)4 x 2 2 xy y 2
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
67.
Учебник Алимова Ш.А. и др.№396(2,4,6)
2) a 2 b 2
Разложить на множители
№395(2,4)
a b
№396(2,4,6)
№397(2,4)
№398(2,4)
4) 1 ( x 2 2 xy y 2 )
6) x 4 x 3 x 1
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
68.
Учебник Алимова Ш.А. и др.№397(2,4)
Вычислить.
382 17 2
2) 2
2
47 19
№395(2,4)
№396(2,4,6)
№397(2,4)
№398(2,4)
47 2 32
4) 2
2
27 2 27 13 13
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2
69.
Учебник Алимова Ш.А. и др.№398(2,4)
Вычислить.
2)37 12,2 22,4 14,6
2
2
№395(2,4)
№396(2,4,6)
№397(2,4)
№398(2,4)
4)97 2,2 99,6 2 2,6 2
a b a b
a 2 b 2 a b 2 a 2 2ab b 2 a b 2 a 2 2ab b 2




































































 mathematics
mathematics








