Формулы сокращенного умножения

1.

Математика
Четырнадцатое февраля
Классная работа
Формулы сокращенного
умножения.

2.

Три пути ведут к знанию:
-Путь размышления самый
благородный,
-Путь подражания самый легкий
-И путь опыта это путь самый горький
Конфуций

3.

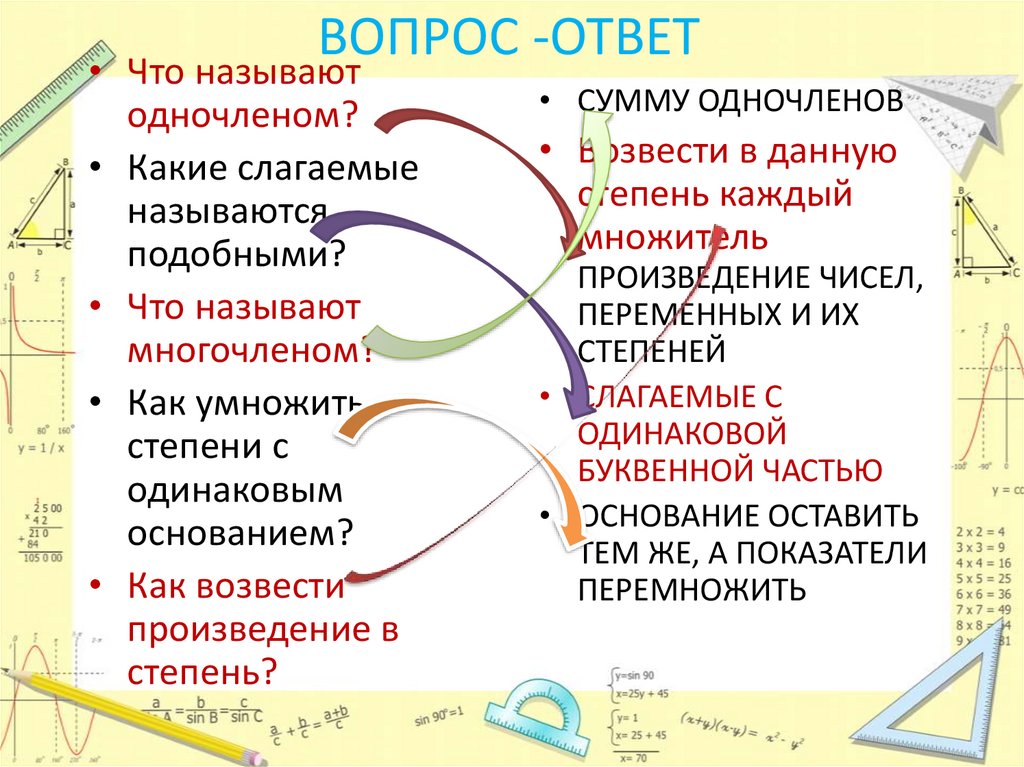
ВОПРОС -ОТВЕТ
• Что называют
одночленом?
• Какие слагаемые
называются
подобными?
• Что называют
многочленом?
• Как умножить
степени с
одинаковым
основанием?
• Как возвести
произведение в
степень?
• СУММУ ОДНОЧЛЕНОВ
• Возвести в данную
степень каждый
множитель
ПРОИЗВЕДЕНИЕ ЧИСЕЛ,
ПЕРЕМЕННЫХ И ИХ
СТЕПЕНЕЙ
• СЛАГАЕМЫЕ С
ОДИНАКОВОЙ
БУКВЕННОЙ ЧАСТЬЮ
• ОСНОВАНИЕ ОСТАВИТЬ
ТЕМ ЖЕ, А ПОКАЗАТЕЛИ
ПЕРЕМНОЖИТЬ

4.

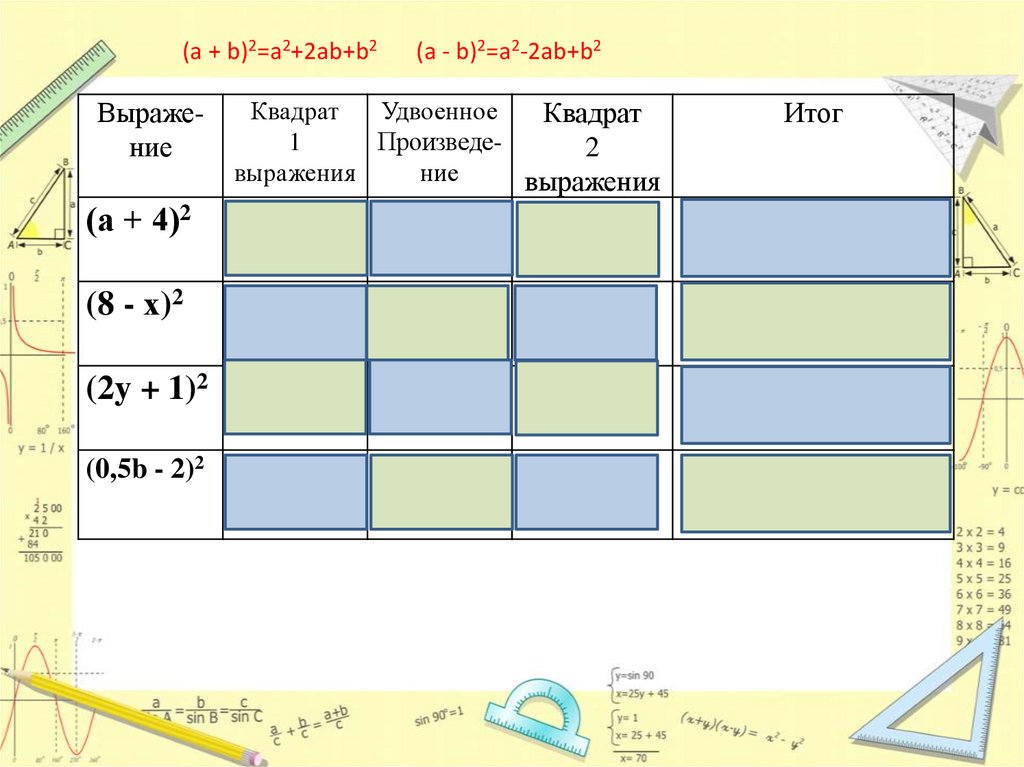
(a + b)2=a2+2ab+b2
Выражение
(а + 4)2
(a - b)2=a2-2ab+b2
Квадрат
Удвоенное
Квадрат
1
Произведе2
выражения
ние
выражения
8a
16
a2
Итог
a2+8a+16
(8 - х)2
64
16x
x2
64-16x+x2
(2y + 1)2
4y2
4y
1
4y2+4y+1
(0,5b - 2)2
0,25b2
2b
4
0,25b2-2b+4

5.

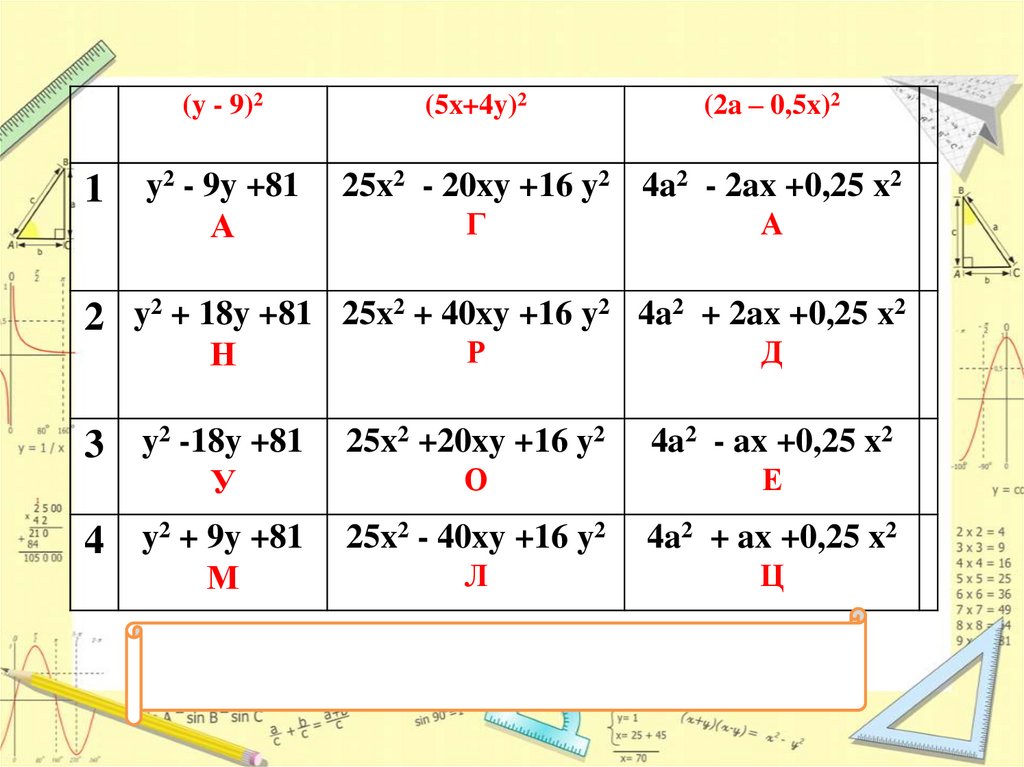
(y - 9)2
1
y2 - 9y +81
А
(5x+4y)2
(2a – 0,5x)2
25x2 - 20xy +16 y2 4a2 - 2ax +0,25 x2
Г
А
2 y2 + 18y +81 25x2 + 40xy +16 y2 4a2 + 2ax +0,25 x2
Н
Р
Д
3 y2 -18y +81
25x2 +20xy +16 y2
4a2 - ax +0,25 x2
О
Е
4 y2 + 9y +81
25x2 - 40xy +16 y2
4a2 + ax +0,25 x2
Л
Ц
Р
А
У
М
У

6.

Представить в виде многочлена:
1) f d
f 2 fd d
2) m 1
m 2m 1
3) 3k 4
9k 24k 16
2
2
2
2
2
2
4) 2 x 7 y
2
4 x 28 xy 49 y
6) b d
7) 5 p 4q
5) c k
2 2
3 2
2
3
4 2
2
4
c 2ck k
2
2
4
b 2b d d
4
2
3
2
6
25 p 40 p q 16q
6
3
4
8

7.

Представить в виде многочлена:
1) s z
s 2 sz z
2) m 1
m 2m 1
3) 4 3k
16 24k 9k
4) 5 x 2 y
25 x 20 xy 4 y
2
2
2
2
2
6) t c
7) 3m 4n
2
5) k p
2
7 2
4
6
3 2
2
2
2
2
k 2k p p
4
2
2
2
t 2t c c
8
4 7
14
9m 24m n 16n
12
6
3
6

8.

Математика
Разность квадратов
двух выражений
ОПРЕДЕЛЕНИЕ
Разность квадратов двух выражений равна произведению их суммы и
разности.
а ² - Ƅ² = ( а - Ƅ)(а – Ƅ)
Левую и правую части можно поменять местами, тогда получаем:
Формула «разность квадратов» очень удобна для разложения многочленов на
множители.

9.

Первичное закрепление
нового материала
Разложи на множители:
1) b² - d²
2) х² - 1
3) - х² +1
4) 36 - с²
5) 4 – 25а²
6) 49а² -100
7) 900 – 81k²
8)с²р² - 1
9) 16х²- 121у²
Проверяем :
1) (b – d)(b + d)
2) (х-1)(х+1)
3) (1-х)(1+х)
4) (6-с)(6+с)
5) (2-5а)(2+5а)
6) (7а-10)(7а+10)
7) (30-9k)(30+9k)
8) (ср-1)(ср+1)
9) (4х-11у)(4х+11у)

10.

Первичное закрепление
нового материала
Разложите на множители,
пользуясь формулой
разности квадратов :
а) (х+9)(х-5)
а) (х+2)²-49 =
б) (х-10+5у)(х-10-5у)
б) (х-10)² - 25у²=
в) (8-у)(2+у)
в) 25- (у-3)²=
г) -6 (2а-2)
г) (а-4)²- (а+2)²=
д) (8у+4)² - (4у-3)²=
Проверяем :
д) (12у+1)(4у+7)

11.

Выполните умножение многочленов, используя
формулу разности квадратов:
• а) (x+2)(x-2)
• б) (y+3)(y-3)
• в) (2x-3y)(2x+3y)
Проверяем :
а) х² - 4
б) у² - 9
в) 4х² - 9у²
• г) (3a-5b)(3a+5b)
г) 9а² - 25b²
• д) (a²-5)(5+a²)
д) а⁴ - 25
• е) (b²+4)(4-b²)
е) 16 -b⁴

12.

Домашнее задание
Выполните умножение многочленов, используя
формулу разности квадратов:
• а) (x+2)(x-2)
• б) (y+3)(y-3)
• в) (2x-3y)(2x+3y)
• г) (3a-5b)(3a+5b)
• д) (a²-5)(5+a²)
• е) (b²+4)(4-b²)

13.

Мало иметь
хороший ум,
главное –
уметь его
применять
Рене Декарт — (1596-1650)
— французский философ,
математик, физик и
физиолог