Ряды Фурье

1.

Ряды Фурье
Опр. 33. Пусть система функций
1 ( x) 2 ( x) n ( x)
ортогональна на [a, b]: C[a, b]
Ряд вида
a1 1( x) a2 2 ( x) an n ( x)
a (x) (32)
n
n
n 1
где ai – числа, называется рядом Фурье по ортогональной на [a, b]
системе функций φ1, φ2 , …, φn

2.

Тригонометрические ряды Фурье
Основная тригонометрическая система функций на [-l ; l ]
1
x
x
2 x
2 x
n x
n x (32*)
, cos
, sin
, cos
, sin
, , cos
, sin
,
2
l
l
l
l
l
l
Опр. 34. Ряд Фурье по основной тригонометрической системе функций
называется тригонометрическим рядом Фурье.
a0
x
x
2 x
2 x
n x
n x
a1 cos
b1 sin
a2 cos
b2 sin
an cos
bn sin
2
l
l
l
l
l
l
a0
n x
n x
bn sin
an cos
2 n 1
l
l
(33)
Если ряд Фурье (33) сходится к некоторой функции f(x) в каждой ее точке
непрерывности, то говорят, что f(x) разлагается в ряд по тригонометрической
системе функций.
Очевидно, это разложение единственно.

3.

a0
x
x
2 x
2 x
n x
n x
f ( x) a1 cos b1 sin
a2 cos
b2 sin
an cos
bn sin
2
l
l
l
l
l
l
Коэффициенты ряда Фурье
1l
a0 f ( x)dx
l l
l
n x
1
an
f ( x) cos
dx
l l
l
l
bn
n x
1
f ( x) sin
dx
l l
l
(34)

4.

Теорема Дирихле.
(достаточные условия сходимости ряда (33) к функции f(x) на отрезке [-l;l])
Пусть на отрезке [-l;l] функция f(x) удовлетворяет условиям:
1) f(x) непрерывна или имеет конечное число точек разрыва первого рода;
2) f(x) монотонна или имеет конечное число точек экстремумов.
Тогда тригонометрический ряд Фурье функции f(x) сходится во всех точках
отрезка [-l; l] и его суммой будет функция S(x), определенная на этом отрезке
следующим образом:
а) S(x)=f(x), если x∈(-l; l) , и x – точка непрерывности функции f(x);
б) S ( x)
f ( x 0) f ( x 0)
, если x∈(-l; l) , и x – точка разрыва функции f(x);
2
f ( l 0) f (l 0)
в) S ( l ) S ( l )
на границе.
2
Причем на любом отрезке не содержащем точек разрыва функции сходимость
тригонометрического ряда Фурье будет равномерной.

5.

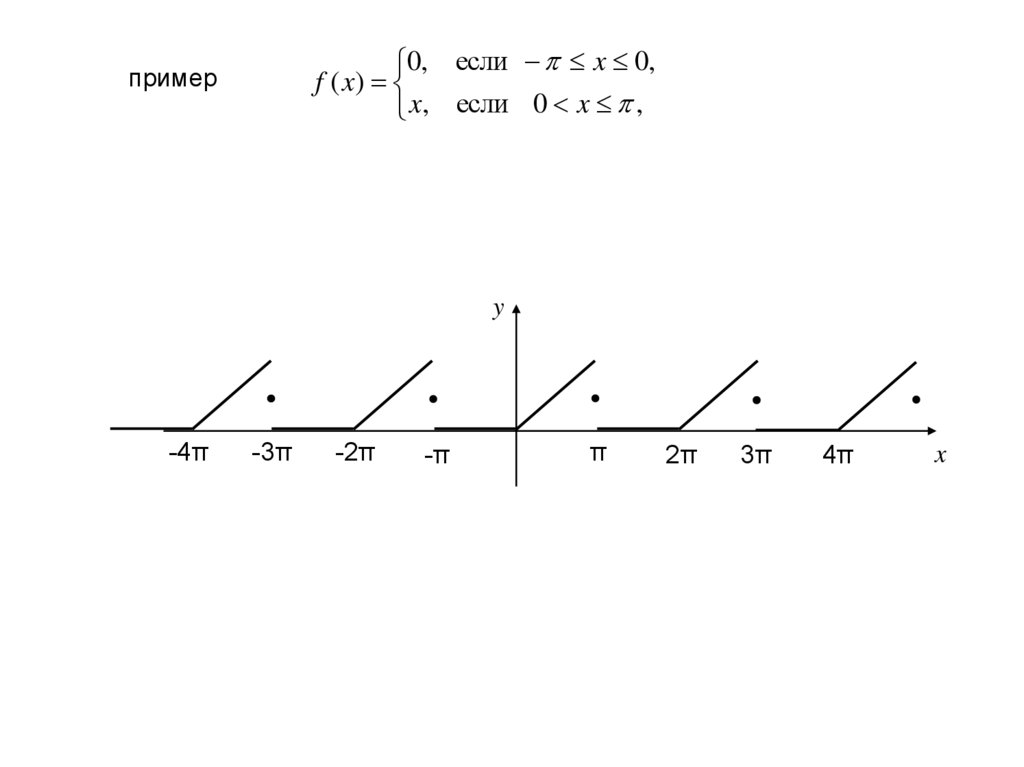
0, если x 0,
f ( x)
x, если 0 x ,
пример
y
-4π
-3π
-2π
-π
π
2π
3π
4π
x

6.

Тригонометрические ряды Фурье для четных и нечетных функций
(неполные ряды Фурье)
2
f(x) – четная => a0
l
Ряд по косинусам:
f(x) – нечетная =>
l
f ( x)dx
0
0
n x
f ( x) cos
dx
l
bn= 0
a
n x
S ( x) 0
an cos
2 n 1
l
a0= 0 an= 0
Ряд по синусам:
2
an
l
l
2
bn
l
n x
S ( x)
bn sin
l
n 1
l
0
(35)
n x
f ( x) sin
dx
l
(36)

7.

Функция, заданная на полуинтервале [ 0 ; l ]
Пусть
f(x) – задана на полуинтервале [ 0 ; l ]
Доопределять f(x) на промежуток [ – l ; 0] можно произвольным образом,
но удобнее сделать это четным или нечетным образом.
Так как доопределение произвольно, то ряд Фурье такой функции
не единственный
пример: f(x) = x-1 задана на [0, π]
y
y
-π
-π
-1
π
доопределим четным образом
x
-1
π
x
доопределим нечетным образом

8.

Функция, заданная на произвольном промежутке
Пусть задана периодическая функция
на интервале [ l ; l +2l ]
f ( x ) с периодом T = 2l
y
S
S
l
-l
λ
λ+2 l
2l
l 2l
l
l
f ( x)dx
l
f ( x)dx
(37)
x

9.

Вывод. При вычислении коэффициентов Фурье для периодической
функции
f ( x ) заданной на интервале [ l ; l +2l ] в силу (37)
1
a0
l
l 2l
1
an
l
1
bn
l
f ( x)dx
l
l 2l
n x
f ( x) cos
dx
l
l 2l
n x
f ( x) sin
dx
l
l
l
(38)