Similar presentations:
Комплексный ряд Фурье. Лекция 8
1.
Комплексный ряд Фурье2.
Тригонометрические формы ряда Фурьеa0
2
2
x(t ) ak cos
kt bk sin
kt
2 k 1
T
T
2
2
ak
x(t ) cos
kt dt , k 0,
T T /2
T
T /2
2
2
bk
x(t )sin
kt dt , k 1,
T T /2
T
T /2
2
3.
Тригонометрические формы ряда Фурье2
x(t ) Ak cos
kt k ,
T
k 0
Ak
2
ak
2
bk
a0
A0
2
амплитудный спектр
Спектр периодического сигнала - дискретный
частота 1-й гармоники
2
1
T
1
F1
T
bk
k arctg
ak
фазовый спектр
3
4.
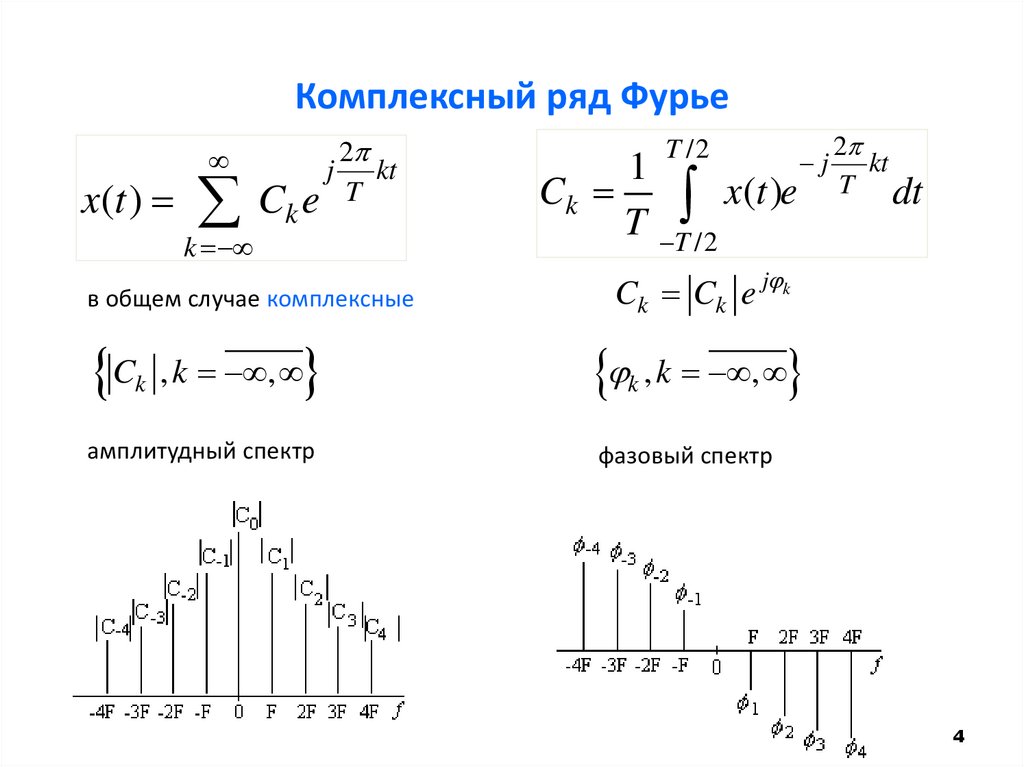
Комплексный ряд Фурьеx(t )
Ck
2
j kt
e T
k
в общем случае комплексные
T /2
1
Ck
x(t )e
T T /2
j
2
kt
T dt
Ck Ck e j k
Ck , k ,
k , k ,
амплитудный спектр
фазовый спектр
4
5.
Тригонометрические формы ряда Фурьеak jbk
Ck
2
ak jbk
C k
2
Отсюда следуют связи
Ck
Ak
2
ak
2
ak
2
bk
a0
C0
2
2
2
bk
a0
A0
2
bk
k arctg
ak
сигнал четный – все синусоидальные компоненты равны 0; сигнал
нечетный – все косинусоидальные компоненты равны нулю (при этом
равна нулю и постоянная составляющая)
5
6.
Тригонометрические формы ряда ФурьеПросуммируем пару
Ck
2
j kt
e T
Ck e
j k
e
C k
j
2
kt
T
2
j kt
e T
Ck e
Ck
j k
e
j
2
j kt
e T
2
kt
T
2
j kt
*
Ck e T
2
2 Ck cos
kt k
T
Тогда ряд Фурье можно записать в тригонометрической форме
2
x(t ) Ak cos
kt k ,
T
2 C , k 0,
k 0
k
Ak
Ak Ck C0 , k 0.
6
7.
Пример.2
T /2
j kt
x(t )e T dt
1
Ck
T T /2
2
2 F
T
U и
C0
U q
T
k и
sin
1
2
U и
2
U
cos
ktdt
k и
T /2
T
T
и
2
и /2
частота повторения импульсов
q T и
скважность импульсной
последовательности
8.
и2
огибающая впервые
пересекает ось абсцисс
f 1 и
Дискреты отстоят друг от друга на
численное
значение
скважности
F 1 T
во сколько раз полуширина
главного лепестка огибающей
спектра больше шага
следования спектральных
составляющих по оси частот
9.
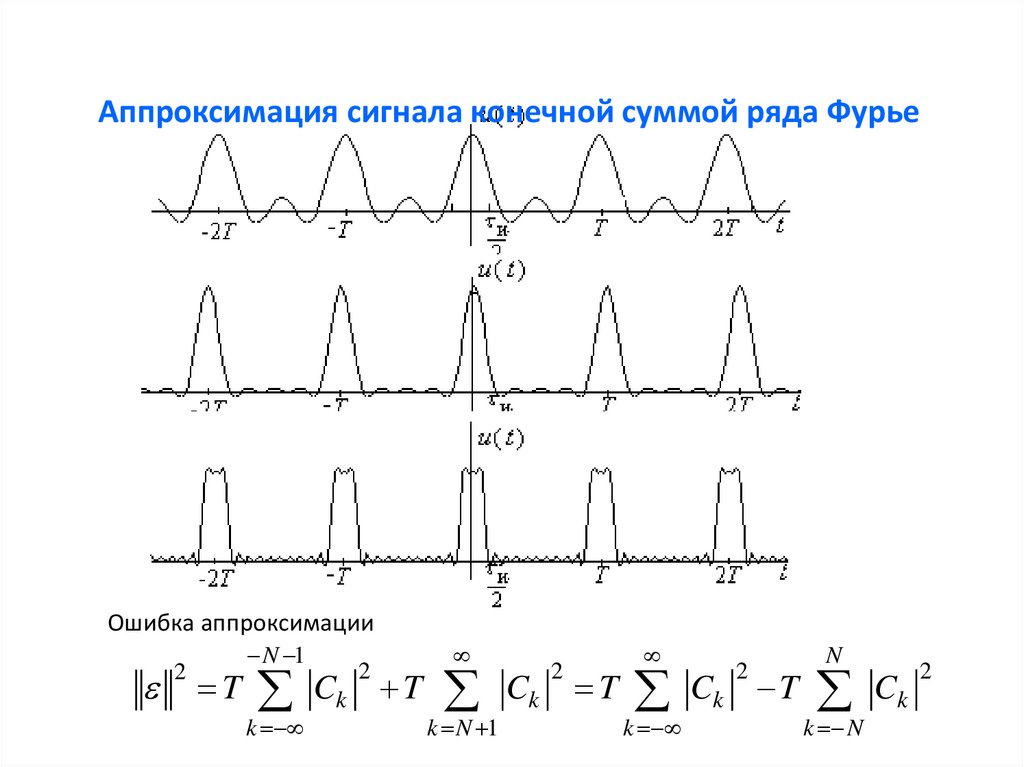
Аппроксимация сигнала конечной суммой ряда ФурьеОшибка аппроксимации
2
T
N 1
k
2
Ck T
k N 1
Ck
2
T
k
2
Ck T
N
k N
Ck
2
10.
Модели детерминированныхсигналов
11.
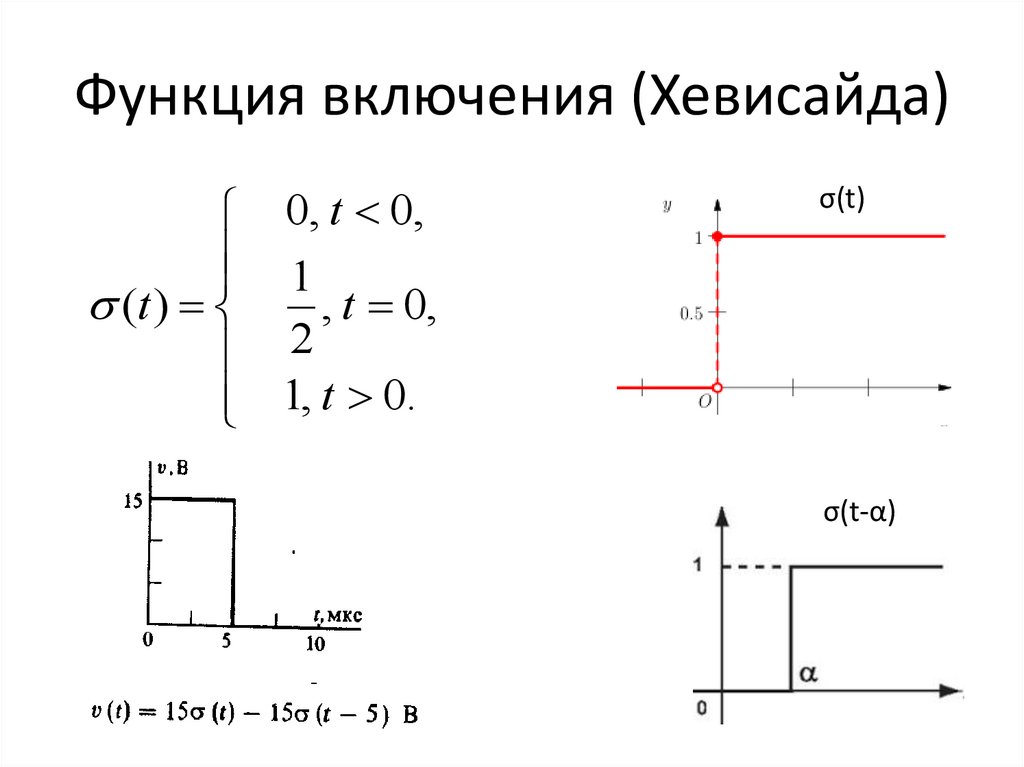
Функция включения (Хевисайда)0, t 0,
1
(t )
, t 0,
2
1, t 0.
σ(t)
σ(t-α)
12.
Дельта-функция (Дирака)1
s (t ) t t
2
2
Дельта-функция, или функции Дирака:
(t ) lim s (t )
0
(
t
)
dt
1
13.
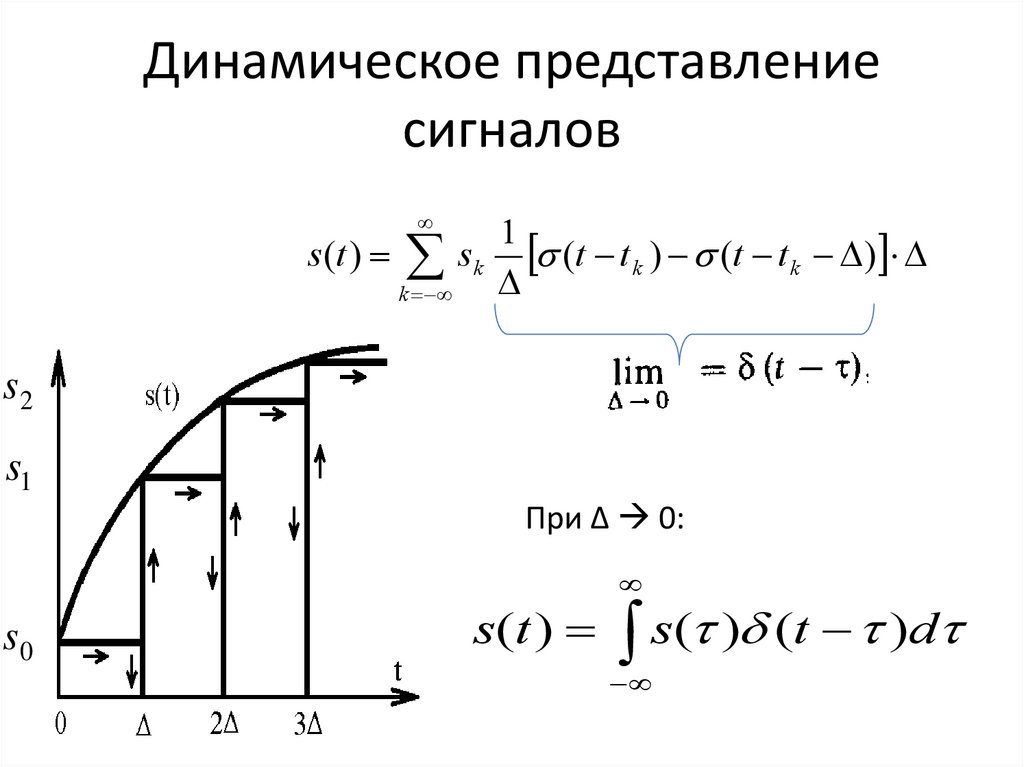
Динамическое представлениесигналов
s(t ) s0 (t ) ( s1 s0 ) (t ) ( s2 s1 ) (t 2 ) ...
s0 (t ) ( s k sk 1 ) (t k )
k 1
s2
s1
При Δ 0:
s0
ds
s(t ) s0 (t ) (t )d
d
0
14.
Динамическое представлениесигналов
1
s (t ) s k (t t k ) (t t k )
k
s2
s1
При Δ 0:
s0
s (t )
s( ) (t )d











 mathematics
mathematics








