Similar presentations:
Ряд Фурье и преобразование Фурье
1.
Ряд ФурьеЖиляков
Ряд Фурье и преобразование Фурье
В. Л. Жиляков
Санкт-Петербургский Государственный Университет, Физический
факультет
12 марта 2022
2.
Тригонометрический ряд ФурьеРяд Фурье
Жиляков
Тригонометрический ряд
Классический тригонометрический ряд – это ряд вида
a0
2
+
X1
=
(ak cos kx + bk sin kx ) ;
k 1
получаемый на базе тригонометрической системы {1,
cos kx ; sin kx ; k 2 Ng
Коэффициенты fa0 ; ak ; bk ; k
или комплексные числа.
2 Ng здесь вещественные
3.
Тригонометрический ряд ФурьеРяд Фурье
Жиляков
Допустим, нам удалось представить непрерывную
функцию в виде тригонометрического ряда. Тогда
коэффициенты разложения однозначно находятся.
Коэффициенты разложения функции в ряд Фурье:
ak
bk
=
=
1
1
Z
f (x ) cos kx dx
Z
f (x ) sin kx dx
4.
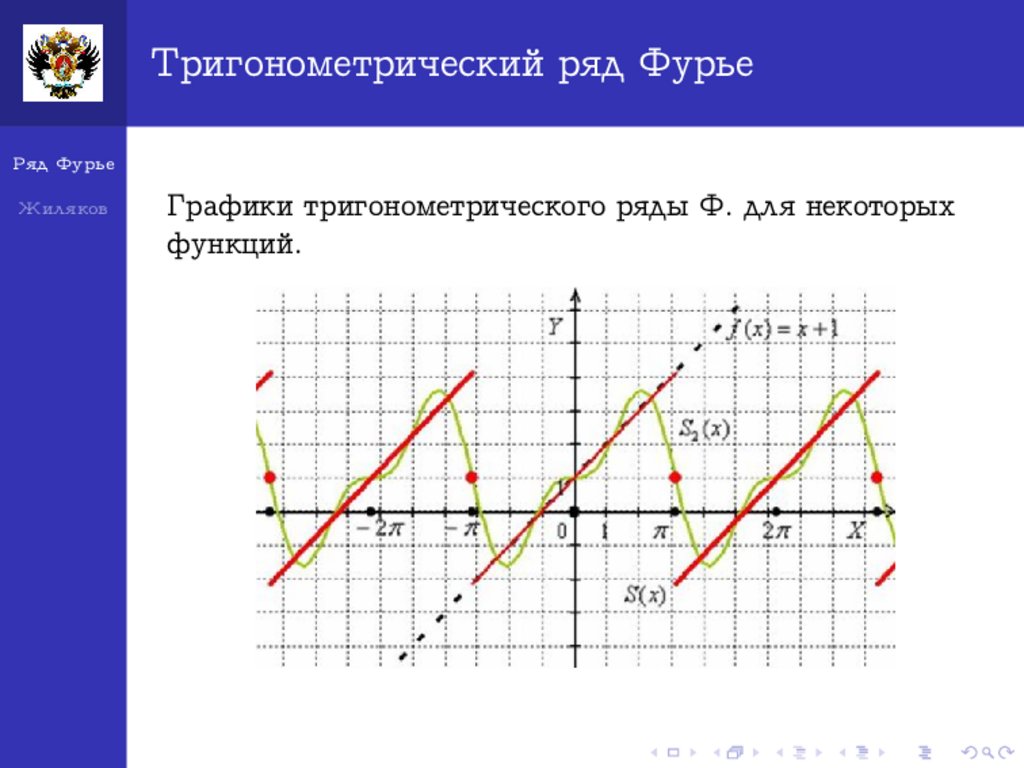
Тригонометрический ряд ФурьеРяд Фурье
Жиляков
Графики тригонометрического ряды Ф. для некоторых
функций.
5.
Тригонометрический ряд ФурьеРяд Фурье
Жиляков
Графики тригонометрического ряды Ф. для некоторых
функций.
6.
Тригонометрический ряд ФурьеРяд Фурье
Жиляков
Тригонометрический ряд Фурье очень важен. Он
необходим
для упрощения анализа
функций
7.
Тригонометрический ряд ФурьеРяд Фурье
Жиляков
Тригонометрический ряд Фурье очень важен. Он
необходим
для упрощения анализа
функций
для работы с радиосигналами
8.
Тригонометрический ряд ФурьеРяд Фурье
Жиляков
Тригонометрический ряд Фурье очень важен. Он
необходим
для упрощения анализа
функций
для работы с радиосигналами
для представления
переодических явлений в других
областях физики







 mathematics
mathematics








