Similar presentations:
Преобразование графика тригонометрической функции у = sin x
1.
Преобразование графикатригонометрической функции
у = sin x
Учитель математики: Заиграева Н.М.
2.
Алгоритм построения графиков• График функции y = sin (x-a) можно получить
параллельным переносом графика функции y = sinx
вдоль оси Ох на а единиц вправо.
• График функции y = sin (x+a) можно получить
параллельным переносом графика функции y = sinx
вдоль оси Ох на а единиц влево.
3.
Сдвиг вдоль оси абсциссПостроить график функции
у=sin(х - 4 )
y = sin x
1,5
+
1
y = sin(x -
4
)
0,5
π/
0
Сдвиг влево
-0,5
-1
-1,5
Построить
график функции
у=sin(х+ )
-
4
1,5
y = sinx
1
y = sin(x +
4
)
0,5
0
-0,5
-
-1
Сдвиг вправо
-1,5
3
4.
Постройте в одной координатной плоскости графикифункций:
y1 = sinx;
у2 = sin(x +
2
);
у3 = sin(x 3 ).
2
5.
Проверка:y1 = sinx;
у2 = sin(x +
2
); у3 = sin(x
3
2
).
y
1
2
0
-1
2
3
2
x
2
3
2
6.
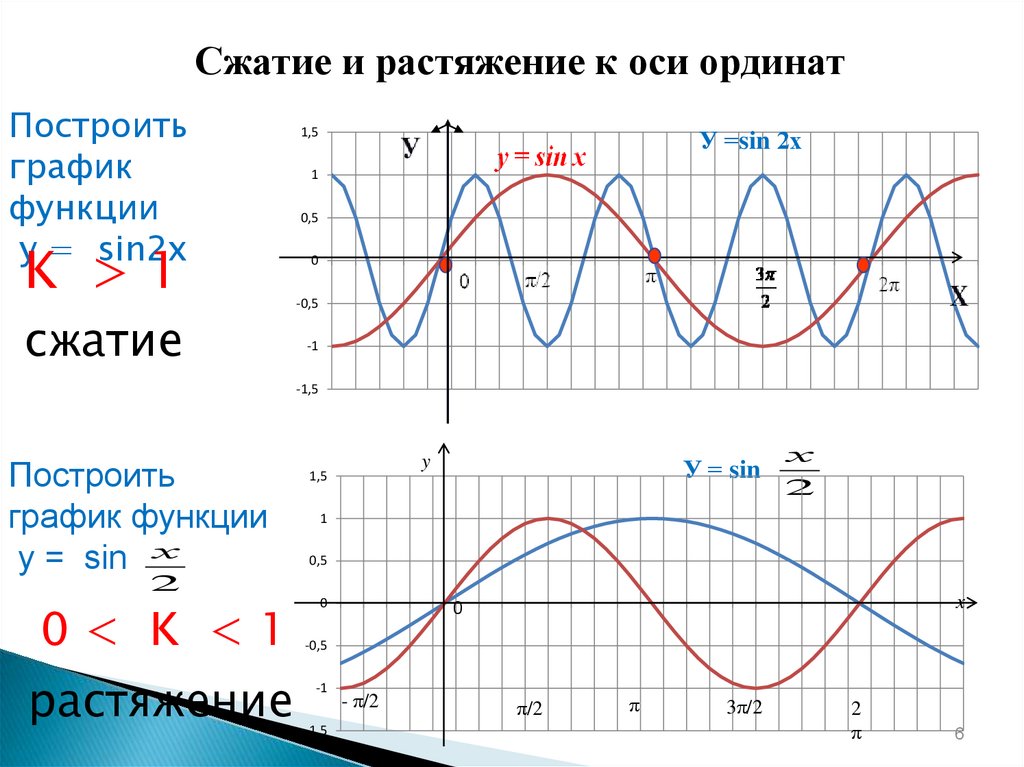
Сжатие и растяжение к оси ординатПостроить
график
функции
у = sin2х
K >1
сжатие
1,5
У =sin 2х
1
0,5
0
-0,5
-1
-1,5
Построить
график функции
у = sin х
y
1,5
У = sin
х
2
1
0,5
2
0< K <1
растяжение
0
x
0
-0,5
-1
-1,5
- π/2
π/2
π
3π/2
2
π
6
7.
Сжатие и растяжение к оси абсциссПостроить график
функции у= 3 sinх
K >
1
растяжение
3,5
3
2,5
2
1,5
1
0,5
0
-0,5
-1
-1,5
-2
-2,5
-3
-3,5
У = 3 sin x
1,5
Построить график 1
0,5
функции
0
у=1/ 3 sinх
0< K <
1 сжатие
у = 1/3 sin x
-0,5
-1
-1,5
7
8.
Постройте в одной координатной плоскости графикифункций:
y1 = sinx;
у2 = 2sinx
у3 = ¼ sinx
9.
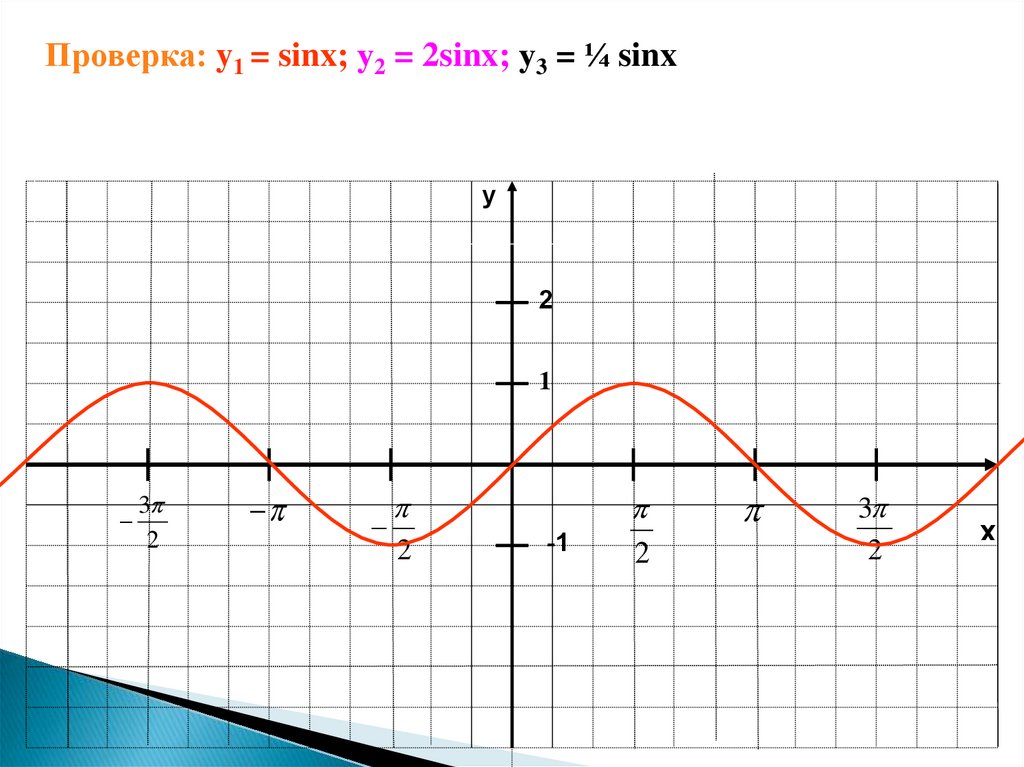
Проверка: y1 = sinx; у2 = 2sinx; у3 = ¼ sinxy
2
1
3
2
2
-1
2
3
2
x
10.
Преобразование графикаy = sinx
4,5
Построить
3,5
график функции2,53
2
у=sinх+3
1,5
y = sinx + 3
4
3
y = sinx
1
+
вверх
Сдвиг вдоль оси ординат
0,5
0
2
-0,5
-1
-1,5
1,5
0,5
Построить
0
график функции-0,5
-1
у=sinх-3
-1,5
1
y = sinx - 3
-2
-2,5
-
-3
-3
вниз
-3,5
-4
-4,5
10
11.
Постройте в одной координатнойплоскости графики функций:
y = sinx;
у = sinx + 2;
у = sinx - 2.
12.
Проверка: y1 = sinx; у2 = sinx + 2; у3 = sinx - 2.y
-1
-2
x
13.
Алгоритм построения графиковy = sin (x) + в :
График функции y = sin (x) + в можно получить
параллельным переносом графика функции y = sin x
вдоль оси Оу на в единиц.
14. Построить график функции:
у1 = sin(x - ) +23
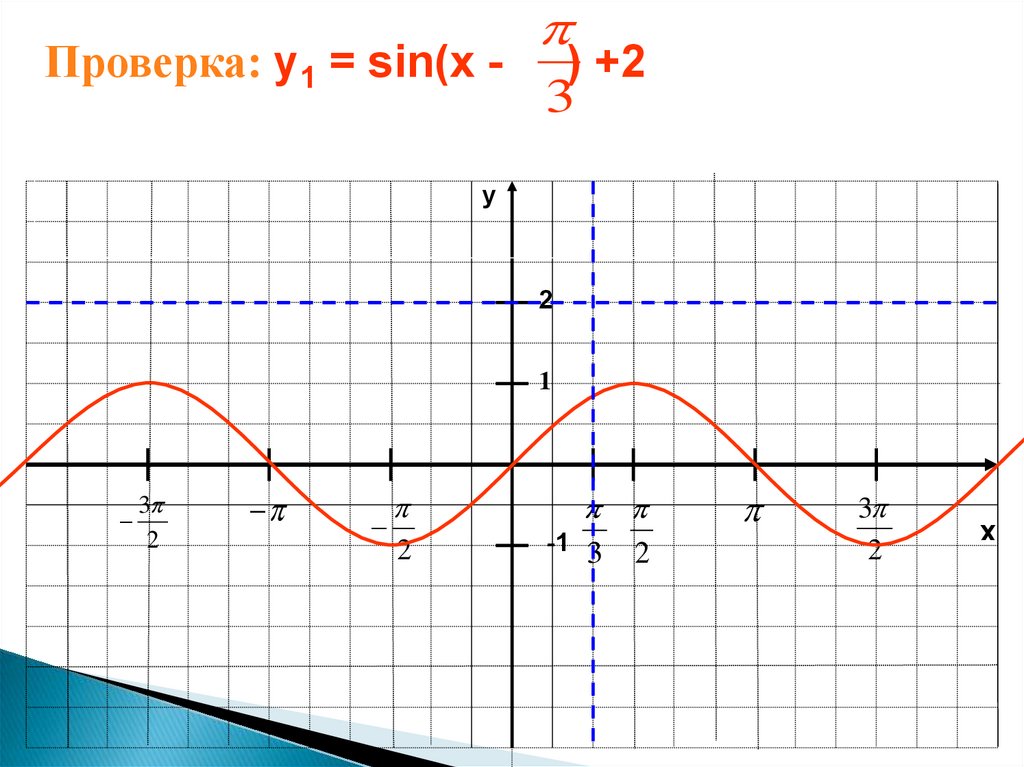
15.
Проверка: у1 = sin(x -) +2
3
y
2
1
3
2
2
-1
3
2
3
2
x
16.
Вывод:График функции y=f(x + t) + m может
быть получен из графика функции
y=f(x) с помощью двух
последовательных сдвигов
на t единиц вдоль оси Ох и на m
единиц вдоль оси Оу.
17.
Самостоятельная работаПостроить графики функций:
Вариант 1.
1. у = sin(x– п/3);
2. у = six+3,5;
3. у = 4sinx
4. у =sin(x – п/4)+3;
5. у = ¼sin(x – п/4)-1;
Вариант 2.
1. y=sin(x - п/4);
2. y=sinx – 1,5;
3. у = 1/3sinx
4. y=sin(x - п/3)-2;
5. y=2sin(x+п/2)-1;














 mathematics
mathematics








