Similar presentations:
Арифметическая прогрессия
1.
2.
ХОЧУ: я хочу пожелать вам, ребята, увеличитьобъём своих знаний в 1,5 раза; хочу пожелать
вам «Ни пуха, ни пера!».
МОГУ: сообщаю, что на уроке можно
ошибаться, сомневаться, консультироваться.
УМЕЮ: мы умеем применять с вами
рациональные способы для решения задач.
ДЕЛАЮ: делаем каждый себе установку
«Понять и быть тем первым, который увидит
ход решения», а вместе с вами сегодня мы
движемся только вперед
3. Кроссворд
1. Как называется график квадратичной функции?2. Математическое предложение, справедливость
которого доказывается.
3. Упорядоченная пара чисел, задающая положение точки
на плоскости.
4. Наука, возникшая в глубокой древности в Вавилоне и
Египте, а учащиеся России начинают её изучать с 7
класса.
5. Линия на плоскости, задаваемая уравнением Y=кх+b
6. Числовой промежуток
7. Предложение, принимаемое без доказательства
8. Прямая, к которой неограниченно приближаются
точки кривой при удалении в бесконечность
9. Название второй координаты на плоскости
10. Французский математик 19 века, «отец» алгебры,
юрист, разгадал шифр, применяемый испанцами в войне
с французами, а нам помог в быстром решении
квадратных уравнений.
4. Проверим
5.
Умение применять формулы …Умение грамотно говорить …
Умение обобщать,
систематизировать …
Умение логически мыслить …
Умение пересказывать …
Умение молчать …
6. Цели урока:
Обобщить теоретические знания по теме;совершенствовать навыки нахождения п-го члена и суммы п
первых членов арифметической прогрессии с помощью
формул;
Развивать познавательный интерес учащихся, учить их
видеть связь между математикой и окружающей жизнью;
развивать грамотную математическую речь;
Воспитывать волю и настойчивость для достижения
конечных результатов;
воспитывать уважительное отношение к одноклассникам.
7. Устная работа:
Являетсяли
заданная
последовательность
арифметической прогрессией, почему?
1.
2.
3.
4.
5.
6.
3; 6; 9; 12; …
-1; -1; -1; …
0; 13; 1; 14; …
xn= 3п – 2;
2
=
25
+
an
n ;
-3; -1; 1; 3; …
8.
• Выразите через аи d а8 , а33 , а100
1
• Найдите а 5 , если а 1 = 4, d =7.
• Найдите а 12 , если а 11= 20, а 13 = 30.
9. Проверь себя!
ПРОВЕРЬ СЕБЯ!1. Да
6. Да
2. Нет
7. 6
3. Нет
8. - 4
4. Да
9. 7
5. Нет
10. - 3
10.
№п/п
Прогрессии
1
Определение
2
Формула n первых членов
3
Название
4
5
Сумма n первых членов
прогрессии
Свойства
Арифметическая
an
d
Геометрическ
ая
bn
g
11.
№п/п
Прогрессии
1
Определение
2
Формула n первых членов
3
Название
Арифметическая an
Геометрическая
bn
an+1= an+d
bn+1=bnq(q≠0,
q≠1)
an= a1+d(n-1)
bn=b1qn-1
d – это разность
Sn
3
4
Сумма n первых членов
прогрессии
Свойства
Sn
(a1 an )n
2
2a1 d (n 1)
n
2
an
an 1 an 1
2
g – это
знаменатель
b1 (q n 1)
Sn
q 1
bn bn 1 bn 1
12.
919
5
7
11
15
17
3
13
13. Математический диктант
МАТЕМАТИЧЕСКИЙ ДИКТАНТ1. Запишите рекуррентную формулу для арифметической
прогрессии.
2. При каком условии арифметическая прогрессия является
возрастающей, при каком – убывающей?
3. Запишите формулу n-го члена арифметической прогрессии.
4. Запишите формулы суммы членов конечной арифметической
прогрессии.
5. Запишите характеристическое свойство арифметической
прогрессии.
14. Проверь!
ПРОВЕРЬ!1.
an an 1 d .
2. Если d > 0, то арифметическая прогрессия возрастающая.
Если d < 0, то арифметическая прогрессия убывающая.
3.
an a1 d n 1 .
a1 an
n
4. S n
2
an 1 an 1
5. an
.
2
2a1 d (n 1)
Sn
n .
2
15. Установи соответствие
УСТАНОВИ СООТВЕТСТВИЕУ
С
Т
А
Н
О
В
И
Т
Е
С
О
О
Т
В
Е
Т
С
Т
В
И
Е
1
2
Формула суммы n первых членов
геометрической прогрессии
Рекуррентное задание арифметической
прогрессии
1
2
3
4
ап а1 d (n 1)
bn b1 q n 1
Sn
an
b1 (1 q n )
,q 0
1 q
an 1 an 1
,n 1
2
5
Sn
a1 a n
2
2
3
Формула n-го члена геометрической
прогрессии
6
a n a1 d (n 1)
4
Разность арифметической прогрессии
7
Sn
5
Формула суммы nпервых членов
арифметической прогрессии
8
6
Рекуррентное задание геометрической
прогрессии
9
Sn
10
q bn 1 : bn
a1 a n
n
2
bn bn 1bn 1 , bn 0, n 1
2a1 d (n 1)
n
2
7
Формула среднего арифметического
11
bn b1 q n
8
Формула суммы бесконечно убывающей
геометрической прогрессии
12
bn 1 bn q
13
q bn 1 bn
9
Формула среднего геометрического
14
d a n 1 a n
10
Формула n-го члена арифметической
прогрессии
15
11
Знаменатель геометрической прогрессии
16
Sn
17
d a n 1 : a n
18
an 1 an d
b1
, q 1
1 q
bn
, q 1
1 q
Sn
16.
12
3
4
5
6
7
8
9
10
11
3
18
2
14
7,9
12
4
15
8
6
10
17. Задача.
Родители ко Дню рождения своего сынаАндрея решили купить и обновить ему
мобильный телефон. Для этого они в
первый месяц отложили 650 рублей, а в
каждый последующий месяц они
откладывали на 50 рублей больше, чем
в предыдущий. Какая сумма будет у
родителей Андрея через 10 месяцев?
…
18.
Дано:a1 650
d 50
n 10
Найти: S10
Решение:
2a1 (n 1)d
Sn
n
2
2 650 9 50
S10
10
2
S10 (1300 450) 5
Ответ:
S10 8750
8750 рублей.
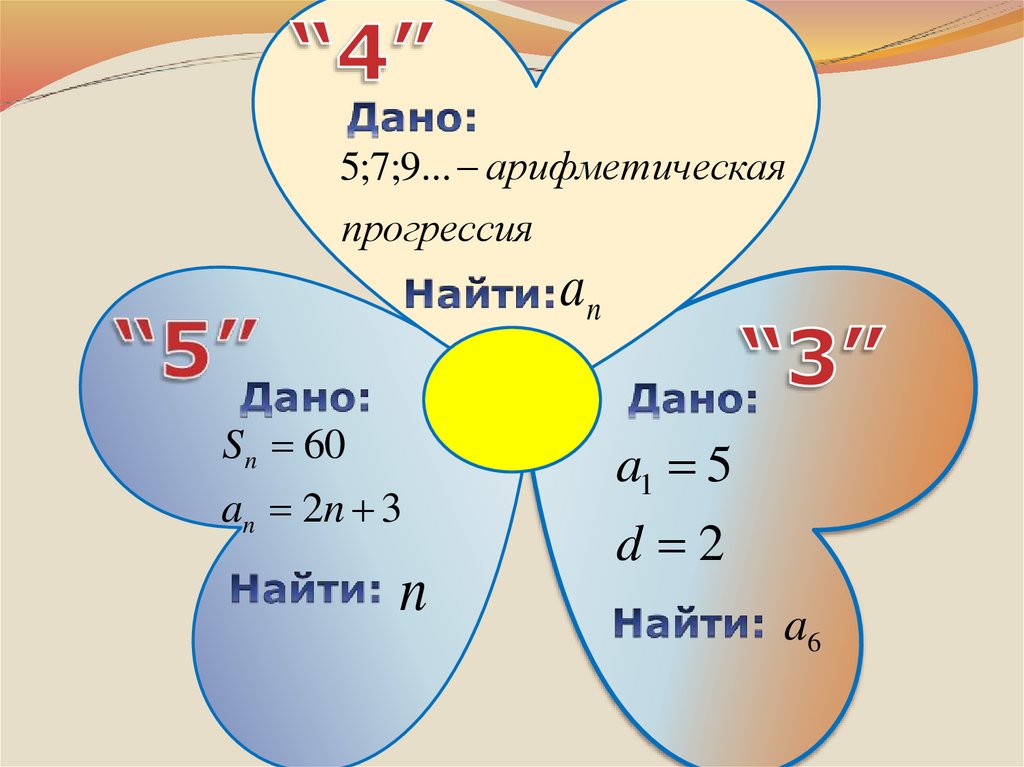
19.
5;7;9... арифметическаяпрогрессия
an
S n 60
an 2n 3
n
a1 5
d 2
a6
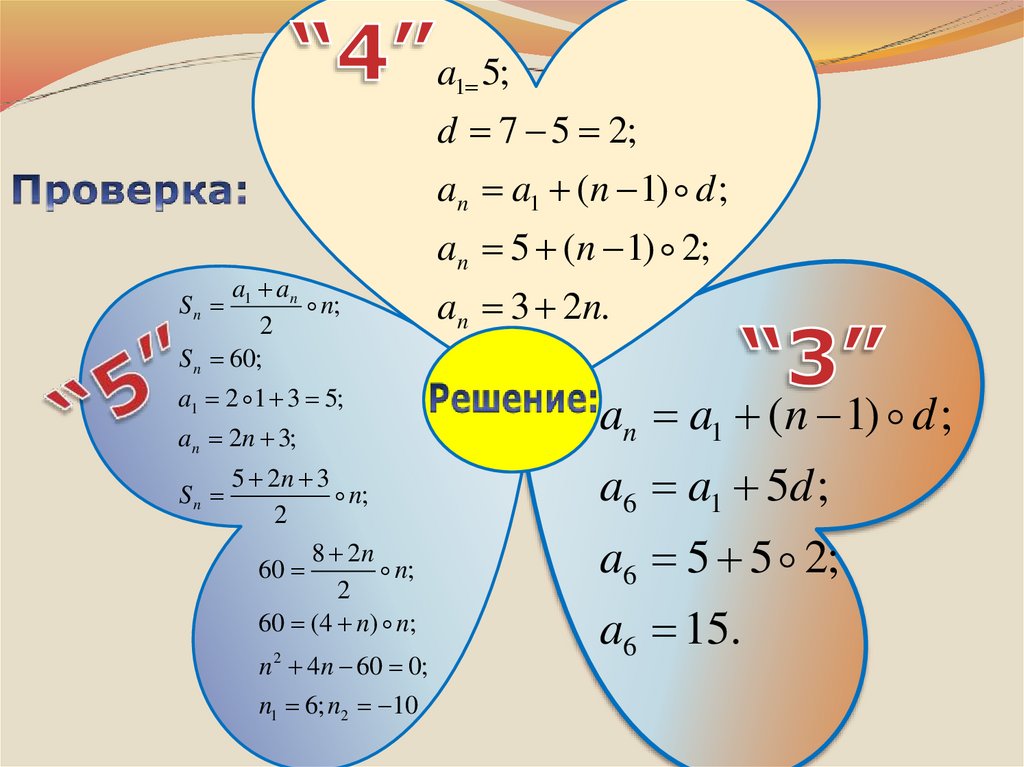
20.
a1 5;d 7 5 2;
an a1 (n 1) d ;
a1 an
n;
2
S n 60;
Sn
a1 2 1 3 5;
an 2n 3;
Sn
5 2n 3
n;
2
8 2n
60
n;
2
60 (4 n) n;
n 4n 60 0;
2
n1 6; n2 10
an 5 (n 1) 2;
an 3 2n.
an a1 (n 1) d ;
a6 a1 5d ;
a6 5 5 2;
a6 15.
21. Задача.
Для участия в международнойматематической игре
«Кенгуру – математика для всех»
в региональный оргкомитет
необходимо подать заявку от школы. В
первый день после указанного срока заявки
на участие подали 5 школ, во второй -7, в
третий - 9 … Через сколько дней в
оргкомитет будет подано 60 заявок
(считая, что полученная закономерность
не будет нарушена)? Сколько заявок
поступит в последний день?
22. Рефлексия.
1.Тест.
Результатом своей личной работы считаю, что я ..
А. Разобрался в теории.
В. Научился решать задачи.
С. Повторил весь ранее изученный материал.
2.
Что вам не хватало на уроке при решении задач?
А. Знаний. Б. Времени.
Д. Решал нормально.
3.
С. Желания.
Кто оказывал вам помощь в преодолении трудностей
на уроке?
А. Одноклассники.
С. Учебник.
Б. Учитель.
Д. Никто.
















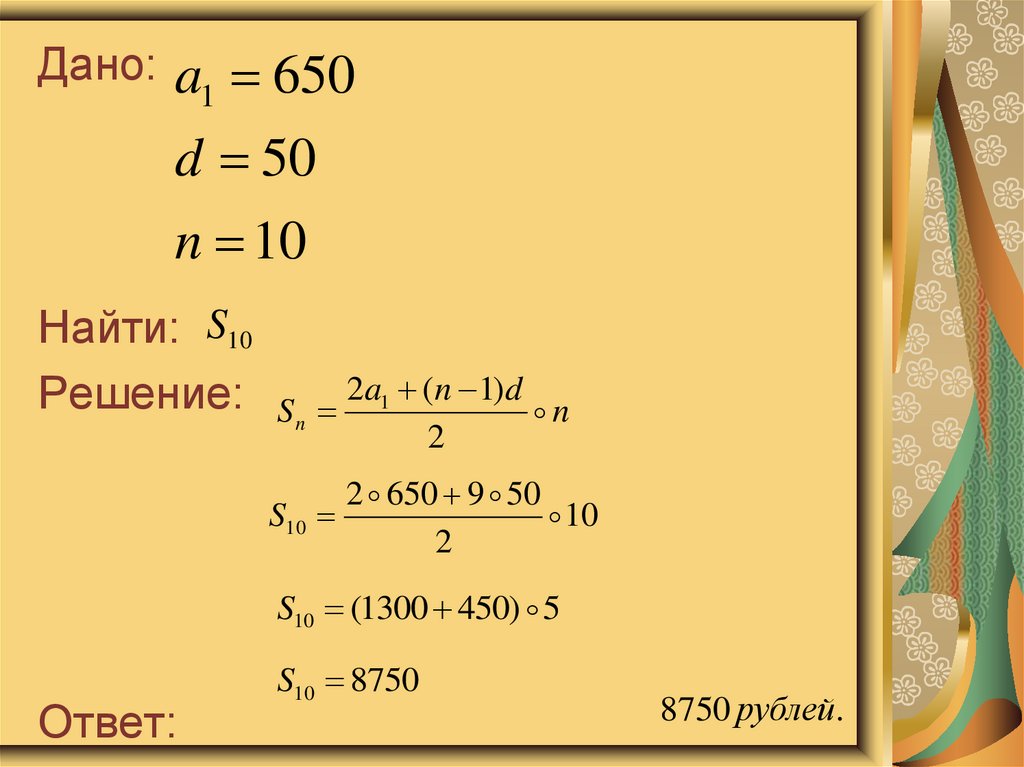


 mathematics
mathematics








