Similar presentations:
Электрические цепи однофазного переменного тока
1. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО ПЕРЕМЕННОГО ТОКА
2. 1. Общие сведения о переменном токе. Получение синусоидальной ЭДС. Графическое изображение. Параметры синусоидального тока.
3.
Переменный ток может бытьпредставлен в виде различных форм
(описан различными способами)
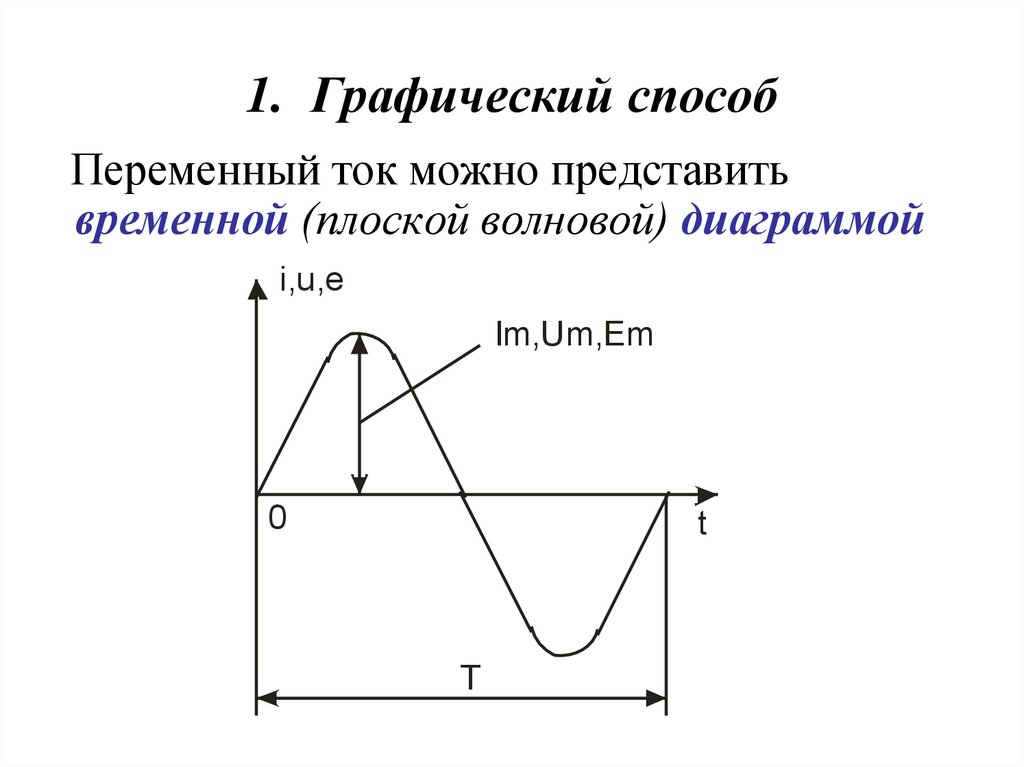
4. 1. Графический способ
Переменный ток можно представитьвременной (плоской волновой) диаграммой
i,u,e
Im,Um,Em
0
t
T
5. Синусоидальные величины характеризуются следующими основными параметрами:
• Период ( Т ) – время, в течение которогопеременная величина совершает полное
колебание.
Единица измерения – секунда (с).
• Частота колебания (циклическая
частота или просто частота) ( f ) –
число периодов в одну секунду.
Единица измерения – 1 Герц (Гц).
6.
Период и частота связаны между собойзависимостью:
1
T
f
7. 2. В виде тригонометрического уравнения
• Наибольшее значение синусоидальнойвеличины называется амплитудным и
обозначается прописными буквами
латинского алфавита с индексами
(Im, Um, Em).
• Значение величины в данный момент
времени называют мгновенным и
обозначают строчной буквой ( i, u, e ).
8.
• Мгновенное значение синусоидальнойвеличины определяют при помощи
тригонометрического уравнения:
i = Im sin ( t + ),
u = Um sin ( t + ),
– круговая (угловая) частота;
= 2 f
– начальная фаза
( t + ) – фаза
9.
Если синусоидальные величиныимеют одинаковую частоту, но
разные начальные фазы, то говорят,
что они сдвинуты по фазе.
Разница начальных фаз называется
углом сдвига фаз.
1 2
10.
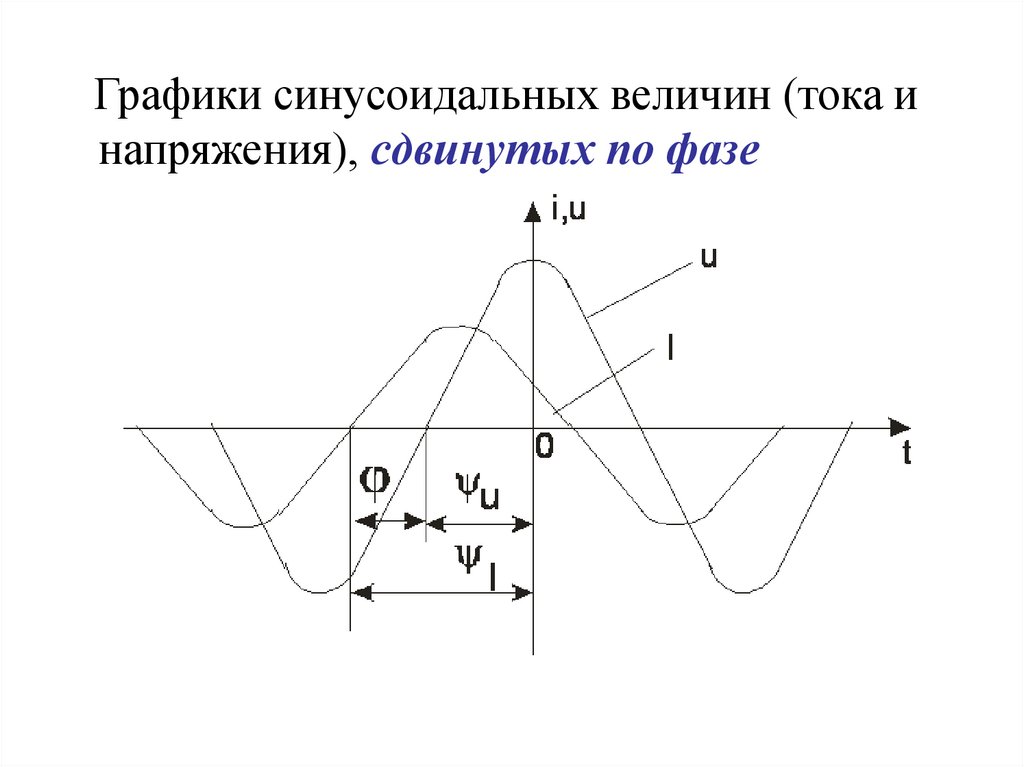
Графики синусоидальных величин (тока инапряжения), сдвинутых по фазе
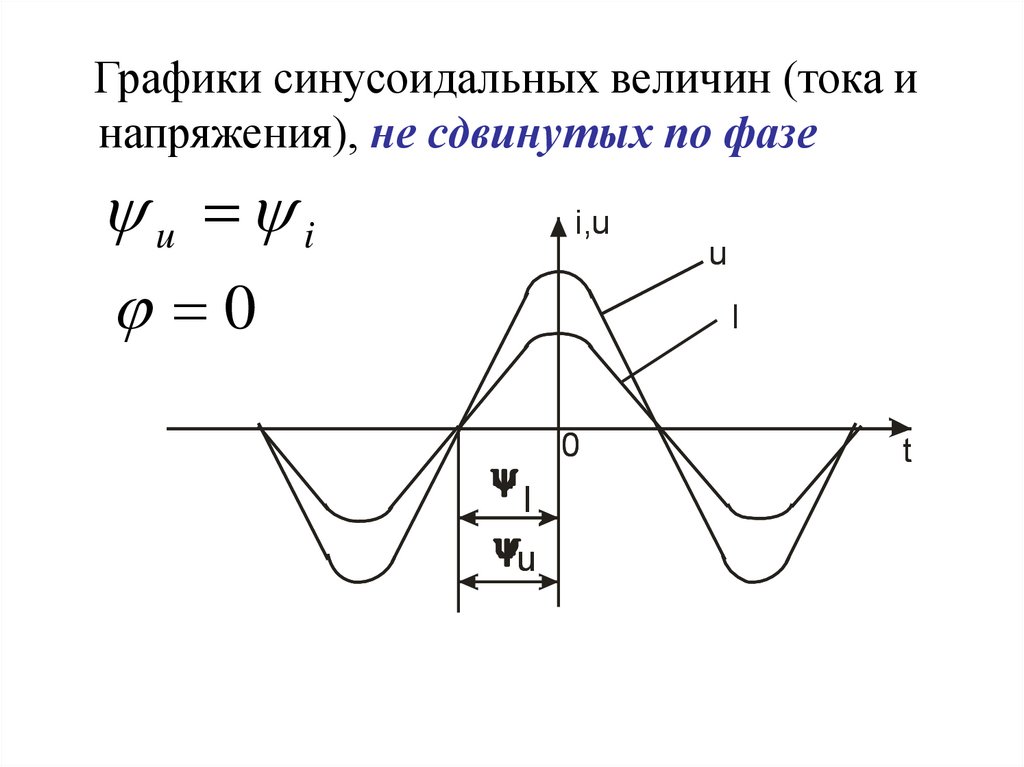
11.
Графики синусоидальных величин (тока инапряжения), не сдвинутых по фазе
u i
0
i,u
u
I
0
I
u
t
12.
Действующее значение переменнойвеличины
I
Im
U
Um
E
Em
2
2
2
0,707 I m
0,707U m
0,707 E m
13.
Среднее значение синусоидальнойвеличины
I
2
I m 0,638 I m
2
U U m 0,638U m
2
E E m 0,638 E m
14. 3. При помощи векторных диаграмм
При расчете цепей переменного тока частоприходится производить операции
сложения и вычитания токов и напряжений.
Когда токи и напряжения заданы при
помощи плоских волновых диаграмм, то
эти операции получаются весьма
громоздкими и производить их неудобно.
Поэтому существует метод построения
векторных диаграмм, который позволяет
существенно упростить действия над
синусоидальными величинами. Суть метода
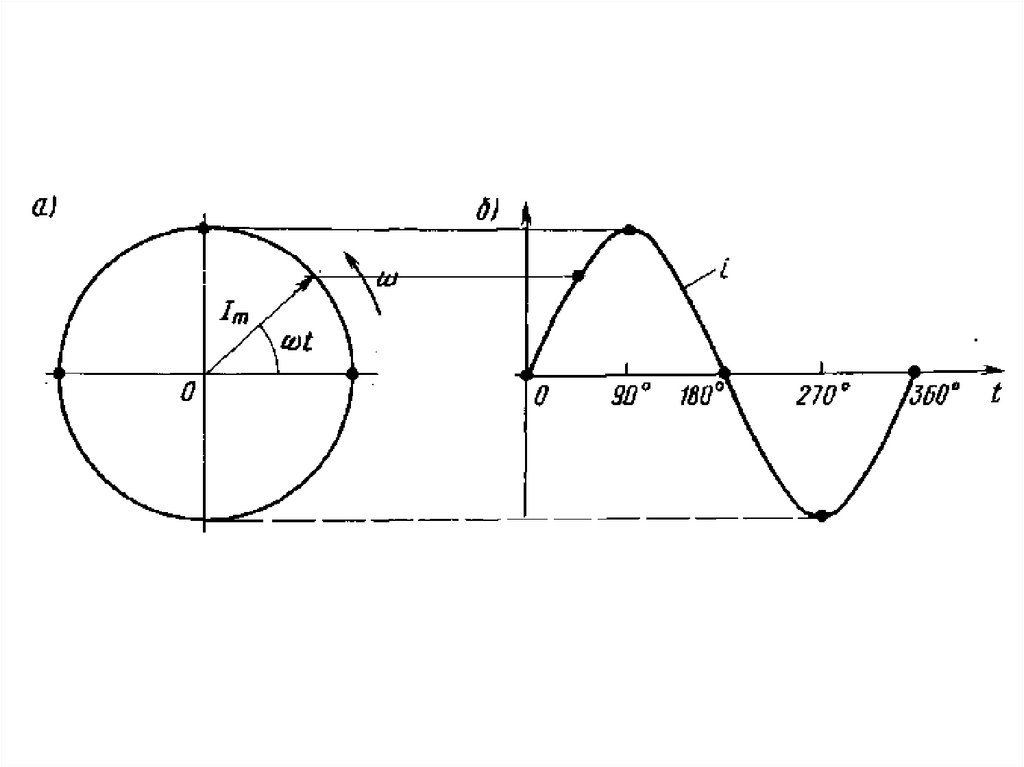
в том, что переменную величину
изображают вращающимся вектором
15.
16.
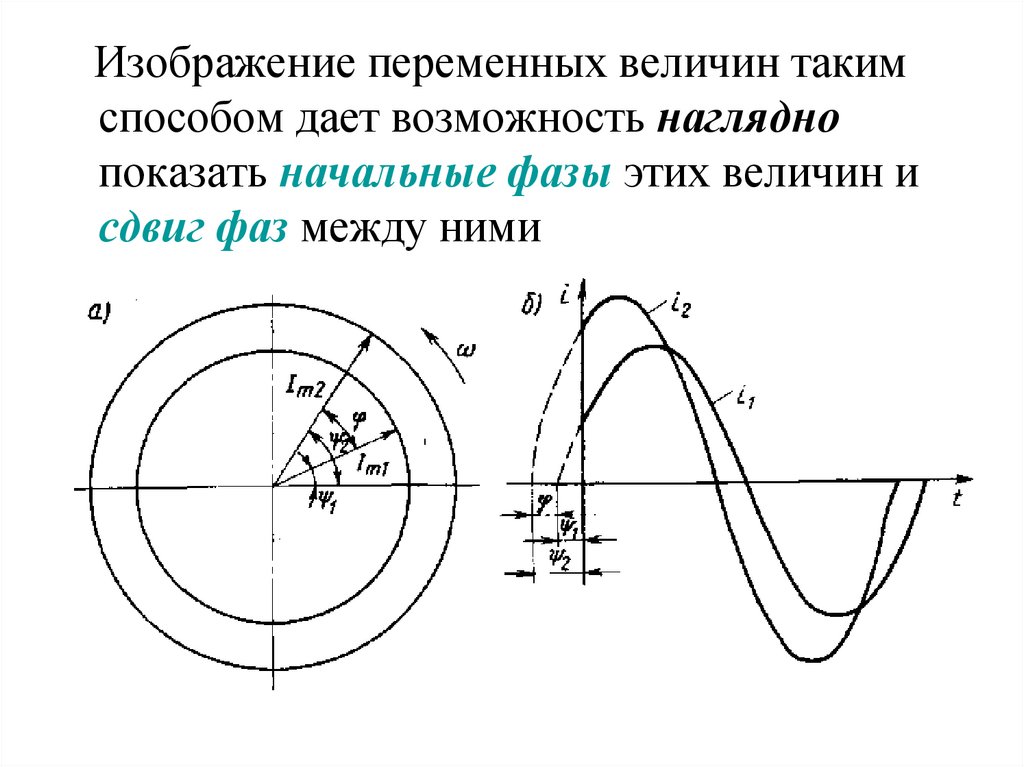
Изображение переменных величин такимспособом дает возможность наглядно
показать начальные фазы этих величин и
сдвиг фаз между ними
17.
• Для построения векторной диаграммывыбирают основной вектор и
направляют его произвольно, а
остальные – в соответствии со сдвигом
по фазе относительно основного.
• Длины векторов выбирают равными
амплитудам периодических величин.
Диаграмму строят в координатном
масштабе (в 1 см – 10 В и т.д.).
18.
• Поворот вектора против часовойстрелки соответствует опережению
по фазе, по часовой – отставанию по
фазе.
• Осуществляют сложение и вычитание
векторов, а вместе с этим сложение и
вычитание самих величин.
19. Домашнее задание
• Евдокимов Ф.Е. Теоретические основыэлектротехники.
Гл.12, § 12.1-12.4, с. 219-231.
• Немцов М.В., Немцова М.Л.
Электротехника и электроника.
Гл. 4, § 4.1-4.5, с. 84-94.














 electronics
electronics








