Similar presentations:
Функция, ее свойства и график. Таблицы значений. Функция у=-х
1. Функция , ее свойства и график
Функцияи график
, ее свойства
Демонстрационный материал
8 класс
Все права защищены. Copyright с 2010. http://www.mathvaz.ru
Copyright с
2. Функция
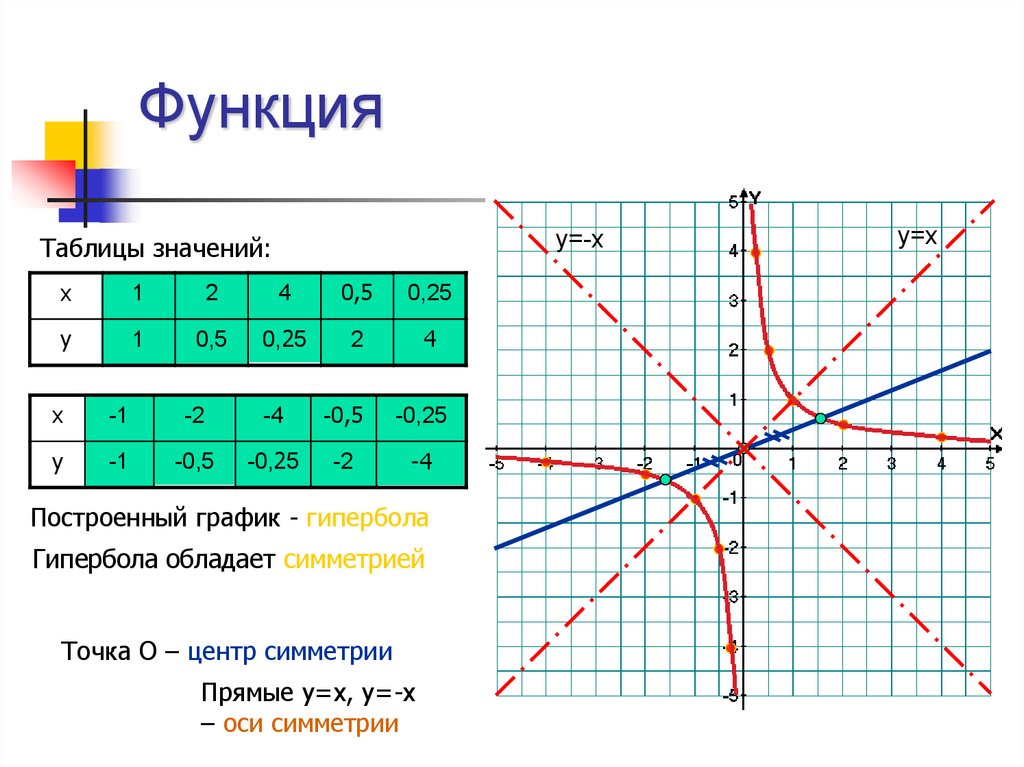
у=-хТаблицы значений:
x
1
2
4
0,5
0,25
y
1
0,5
0,25
2
4
x
-1
-2
-4
-0,5
-0,25
y
-1
-0,5
-0,25
-2
-4
Построенный график - гипербола
Гипербола обладает симметрией
Точка О – центр симметрии
Прямые у=х, у=-х
– оси симметрии
у=х
3. Функция
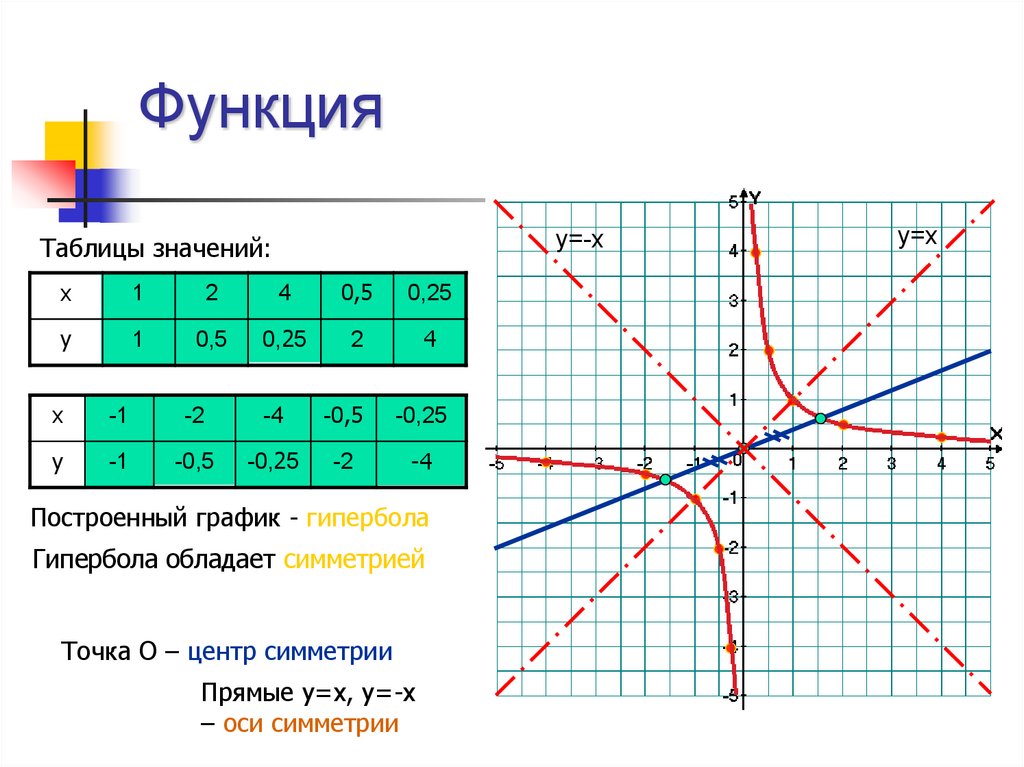
у=-хТаблицы значений:
x
1
2
4
0,5
0,25
y
1
0,5
0,25
2
4
x
-1
-2
-4
-0,5
-0,25
y
-1
-0,5
-0,25
-2
-4
Построенный график - гипербола
Гипербола обладает симметрией
Точка О – центр симметрии
Прямые у=х, у=-х
– оси симметрии
у=х
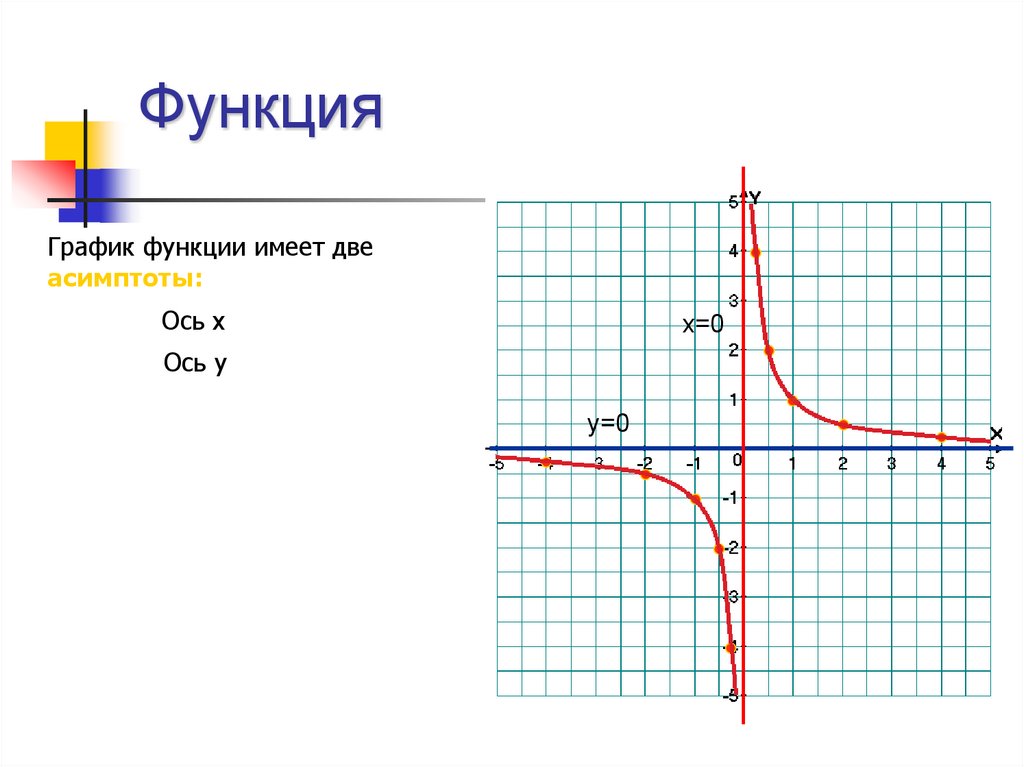
4. Функция
График функции имеет двеасимптоты:
Ось х
х=0
Ось у
у=0
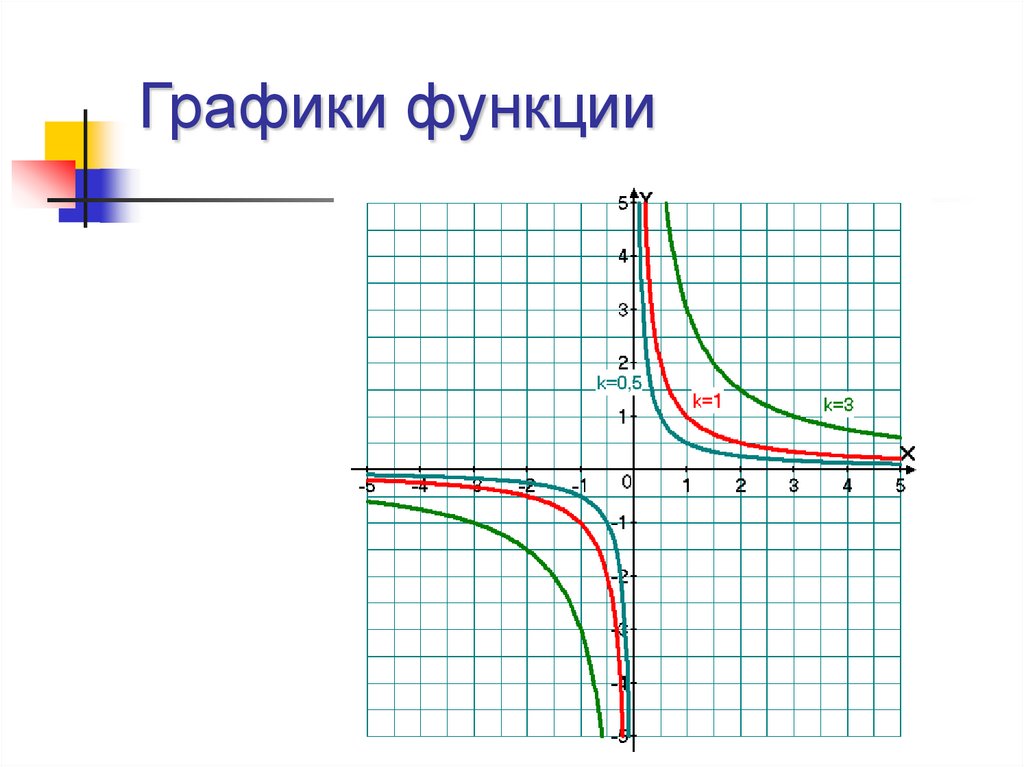
5. Графики функции
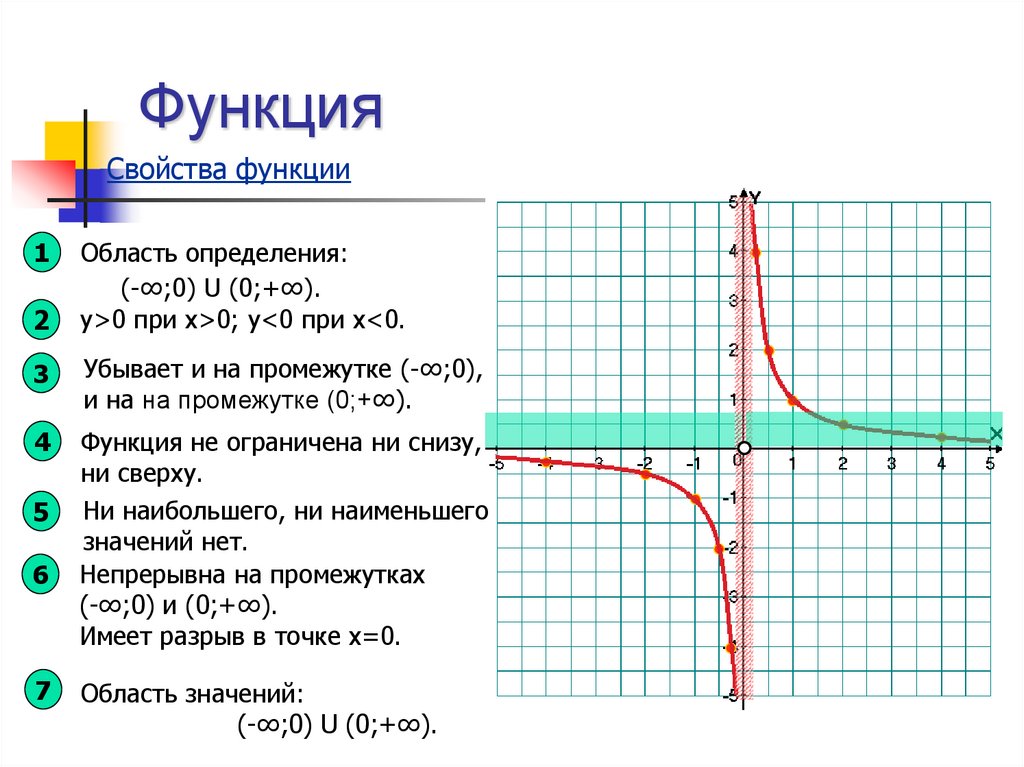
6. Функция
Свойства функции1
2
Область определения:
(-∞;0) U (0;+∞).
у>0 при х>0; y<0 при х<0.
3
Убывает и на промежутке (-∞;0),
и на на промежутке (0;+∞).
4
Функция не ограничена ни снизу,
ни сверху.
Ни наибольшего, ни наименьшего
значений нет.
Непрерывна на промежутках
(-∞;0) и (0;+∞).
Имеет разрыв в точке х=0.
5
6
7
Область значений:
(-∞;0) U (0;+∞).
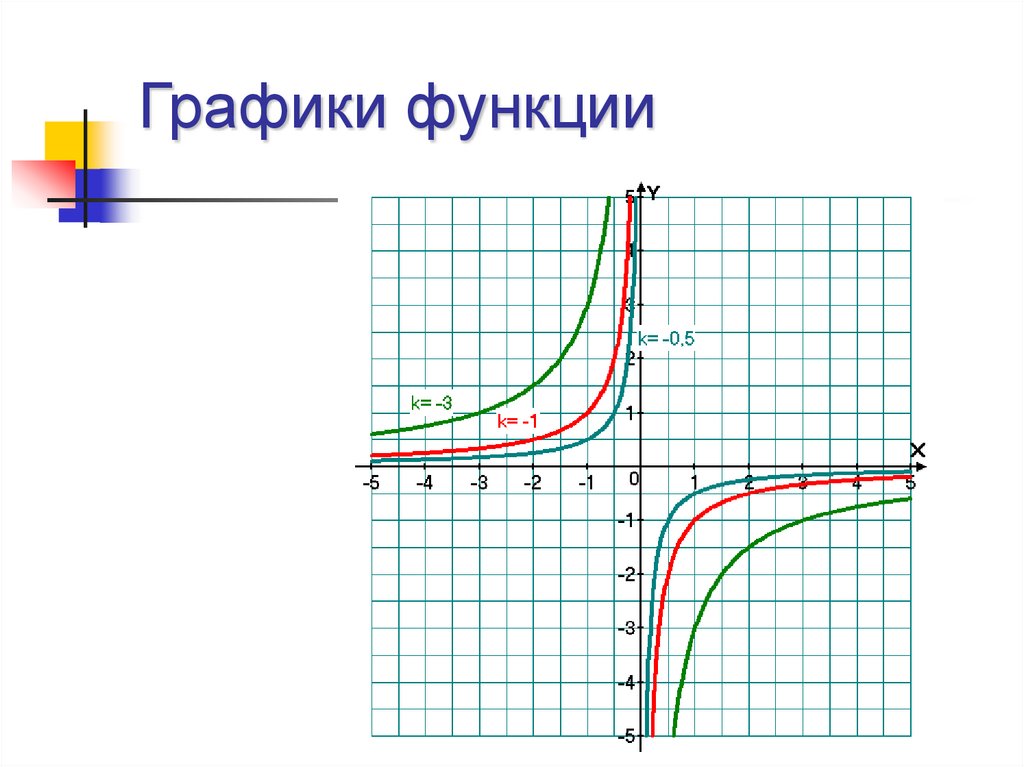
7. Графики функции
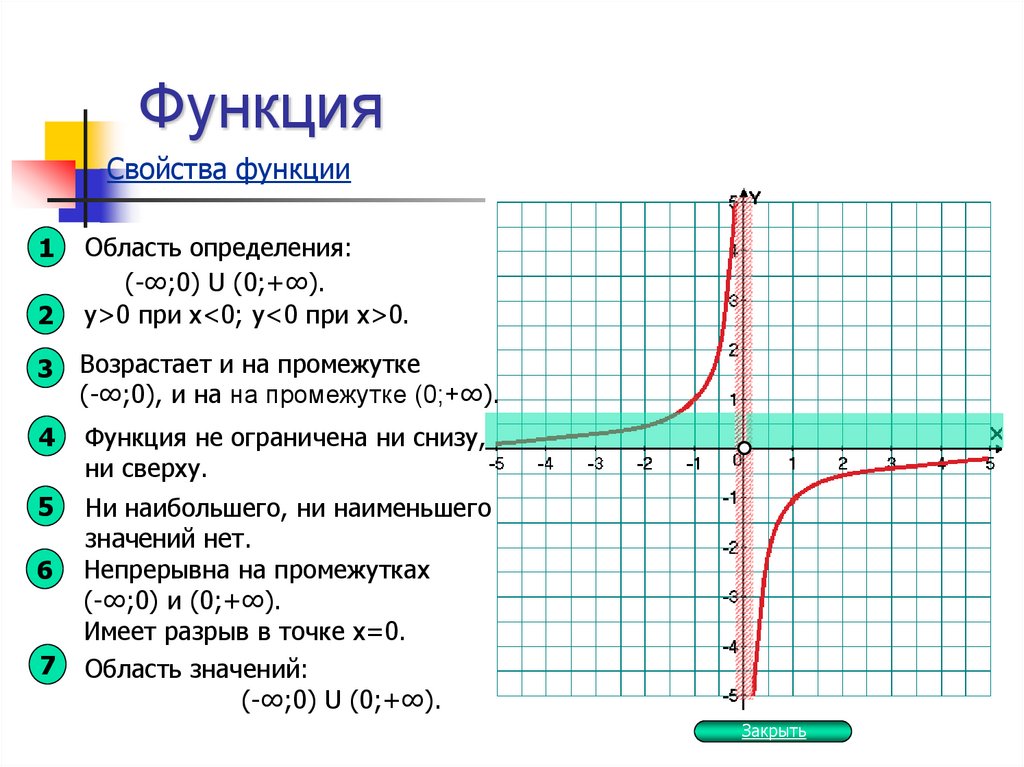
8. Функция
Свойства функции1
2
Область определения:
(-∞;0) U (0;+∞).
у>0 при х<0; y<0 при х>0.
3
Возрастает и на промежутке
(-∞;0), и на на промежутке (0;+∞).
4
Функция не ограничена ни снизу,
ни сверху.
5
Ни наибольшего, ни наименьшего
значений нет.
Непрерывна на промежутках
(-∞;0) и (0;+∞).
Имеет разрыв в точке х=0.
Область значений:
(-∞;0) U (0;+∞).
6
7
Закрыть

 mathematics
mathematics