Similar presentations:
Решение логарифмических уравнений. Теория логарифма
1. Решение логарифмических уравнений
МКОУ «Горшеченская СОШ имениН. И. Жиронкина»
Решение
логарифмических
уравнений
Учит ель Трунаева С.Т.
2.
Расскажи – и я забуду,Покажи – и я запомню,
Дай мне сделат ь самому – и я
научусь!
Кит айская мудрост ь
3. Теория логарифма
• Что называется логарифмом?• Записать основное
логарифмическое тождество.
• Свойства логарифмов
4. Свойства логарифмов
log a 1 0 log a а 1log a ( ху) log a х log a у
х
log a log a х log a у
у
r
log a х r log a х
log a r х
log a
1
log a х
r
log b х
х
log b a
5. Устные задания
log 5 5log 7 1
lg 0,01
log 2
2
1
0
-2
1/2
log 3 81
• 4
2 log2 5
• 5
10
lg15
• 15
log 2 8
lg 100
log 5 125
log 4 64
3
2
3
3
1
log 3
27
log 0 , 5 32
• -3
log 1 9
• -2
3
• -5
6. Решите устно
log 8 16 log 8 4 log 3 33 log 3 11lg 34 lg 3,4
lg 25 lg 4
log 3 log 3 27
log 2 log 2 16
5
log 5 49
log 5 7
log5 2 1
log 3 64
log 3 4
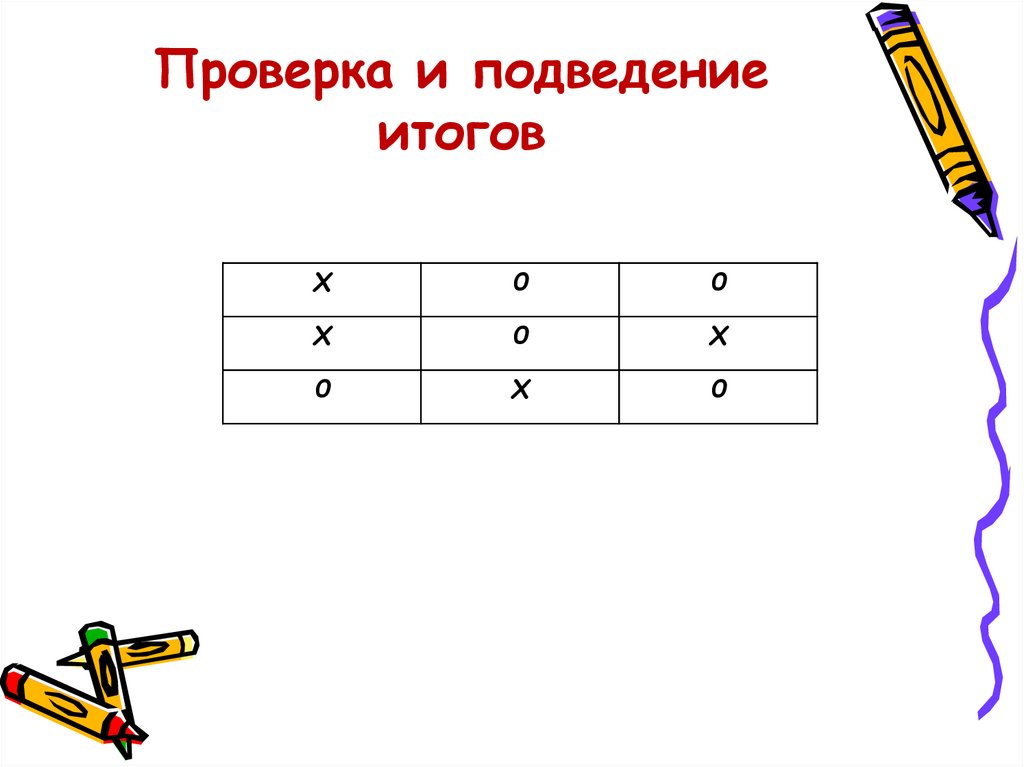
7. Математический диктант «Крестики-нолики»
Мат емат ический дикт ант «Крест ики-нолики»1
2
3
4
5
6
7
8
9
ДА – Х, НЕТ – О
Вопросы:
1.Логарифмом числа в по основанию а называется показатель
степени , в которую надо возвести а, чтобы получить в
2.Логарифмическая функция убывает при а<0
3.Сумма логарифмов чисел равна логарифму суммы чисел
4.Область определения логарифмической функции - множество
положительных чисел
5.Логарифм 1 равен 1
6.Логарифм степени равен произведению показателя степени на
логарифм основания
7.
=2
8. Логарифмическая функция возрастает при а>1
9. Область значений логарифмической функции - множество
положительных чисел
8. Проверка и подведение итогов
Х0
0
Х
0
Х
0
Х
0
9. Найдите корни уравнения
loq x 4 x3
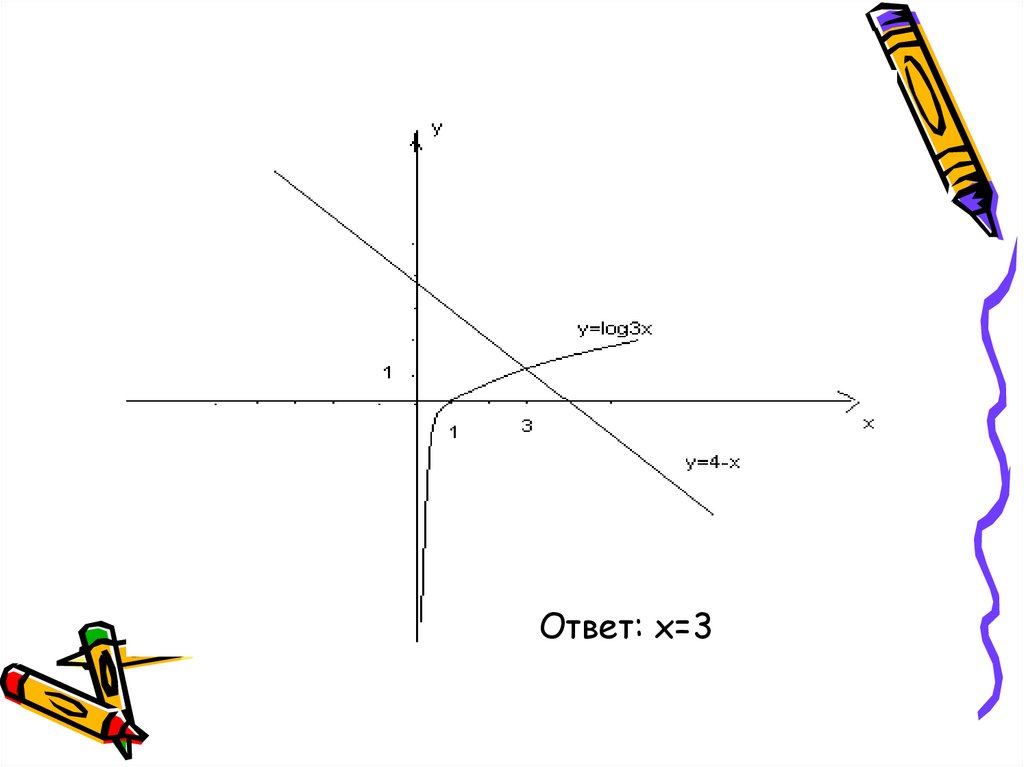
10.
• Для решения ЛУ графическим методом надопостроить в одной и той же системе координат
графики функций, стоящих в левой и правой
частях уравнения и найти абсциссу их точки
пересечения
Найти корни уравнения
loq
3
x 4 x
Так как функция у log3 x возрастающая, а
функция у = 4-х убывающая на (0; + ∞),то
заданное уравнение на этом интервале имеет
один корень.
11.
Ответ: х=312. Простейшее логарифмическое уравнение
log a x b x a , x 0b
Например:
log 3 x 2
одз : x 0
x 3
2
x 9; 9 одз
Ответ : 9
13.
№1. Решить уравненияa) log 2 x 1 3
log 2 x 1 log 2 2
x 1 8
x 7;7 одз
одз :
3
x 1 0
x 1
Ответ : 7
14.
б) log 2 x 1 log 2 x 3 3x 1 0
x 1
одз :
x 1
x 3 0 x 3
log 2 x 1 x 3 log 2 23
x2 4x 3 8
x2 4x 5 0
x1 1;
1 одз
x2 5; 5 одз
Ответ :1
15.
в) lg x 3 2 lg 2 lg xРешение
г ) log 7 36 log 7 3x 12 log 7 4
Решение
д) log x log 4 x 1,5 0
2
4
Решение
Далее
16. Решение уравнения под буквой в
в) lg x 3 2 lg 2 lg xx 3 0 x 3
одз :
x 0
x 0
x 0
lg x 3 lg x lg 22
lg x x 3 lg 4
Согласно свойству:
p log a b log a b p
x 2 3x 4
x 2 3x 4 0
x1 1;
1 одз
x2 4; 4 одз
Ответ :1
Назад
17. Решение уравнения под буквой г
г ) log 7 36 log 7 3x 12 log 7 4одз :
log 7 3 x 12 log 7 36 log 7 4
3 x 12 0
36
log 7 3 x 12 log 7
4
3 x 12 9
3 x 12
x 4
3 x 21
x 7; 7 одз
Ответ : 7
Назад
18. Решение уравнения под буквой д
д) log 24 x log 4 x 1,5 0одз : x 0
1
log x log 4 x 1,5 0
2
Обозначим : log 4 x t log 4 x 1
x 4; 4 одз
t 2 0,5t 1,5 0
2
4
log 4 x 1,5
x 4 1,5
x
1
4
3
2
1
t1 1
x
t 2 1,5
1
x ;
8
43
1
одз
8
Ответ : 0,125;4
Назад
19. Домашнее задание
• №514 (в,г)• №518 (в,г)
• №520 (в,г)
20. Логарифмическая «комедия 2>3»
Логарифмическая «комедия 2>3»• Комедия начинается с
неравенства,
бесспорно правильного.
1 1
4 8
2
3
• Затем следует
1 1
преобразование
тоже не внушающее сомнения
2 2
• Большему числу
соответствует больший
2
3
логарифм, если функция
1
1
1
1
lg lg
2
lg
3
lg
возрастает, значит,
.
2
2
• После сокращения на
• Имеем 2>3.
• В чем ошибка этого
доказательства?
1
lg
2
2
2







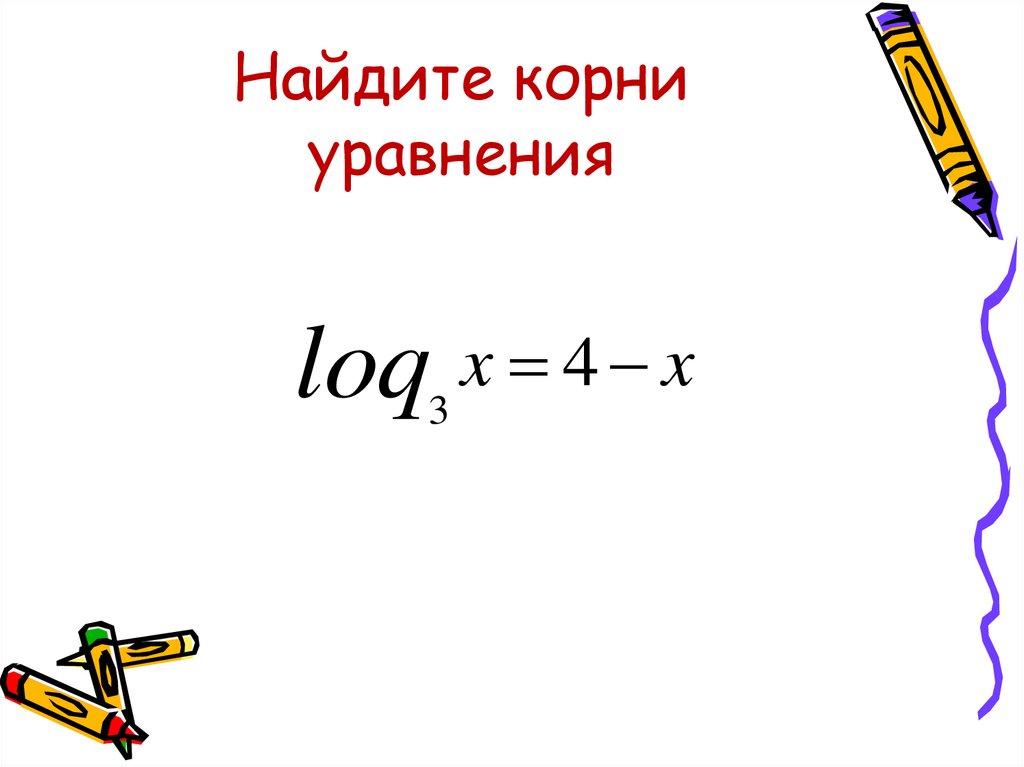











 mathematics
mathematics








