Similar presentations:
Приёмы решения целых уравнений (9 класс)
1.
Приёмы решения целыхуравнений
Янтикова Н.М.
Киреевский ЦО №1.
2.
Цель урока: закрепление умений и навыковрешения уравнений различными приёмами
3.
"Уравнение – это золотой ключ,открывающий все математические
сезамы"
С. Коваль
4.
№ 358(б)Решить уравнение: (x2-x-16)(x2-x+2)=88
Решение:
х2-x=t,
(t-16)(t+2)=88,
t2-14t-120=0,
t=-6, t=20.
t=-6
х2-х= -6,
х2-х=20,
х2-х+6=0
х2-х-20=0
Д=1-24=-23<0-корней нет
х=-4, х=5.
Ответ:х=-4, х=5.
5.
Какое уравнение можно решатьизвлечением квадратных корней?
6.
Тх2 = 9
7.
Какое уравнение решается вынесениемобщего множителя за скобки?
8.
Ау2 - 6у = 0
9.
Какое уравнение можно легко решить спомощью разложения многочлена на
множители?
10.
Рх3 - 8х2 - х + 8 = 0
11.
Какое уравнение легко решаетсяграфически?
12.
Тх3 = 4х - 1
13.
Какое уравнение удобно решить потеореме Виета?
14.
Ах2 + 5х + 4 = 0
15.
Какое уравнение можно решитьразложением разности квадратов?
16.
Лх2 - 4 = 0
17.
Какое уравнение решается методомвведения новой переменной?
18.
Ь(2х2+ 3)2-12(2х2 + 3)+11=0
19.
Каким способом решается последнееуравнение?
20.
Я х3+ 2х2+3х+2=021.
(х-1)(х-2)(х-3)(х-4)=840.((х-1)(х-4))((х-2)(х-3))=840,
(х2-5х+4)(х2-5х+6)=840,
х2-5х+4=t,
t(t+2)=840,
t2+2t-840=0,
t=28,
t=-30,
х2-5х+4=28,
х2-5х+4=-30,
х=8, х=-3.
х2-5х+34=0,
Д=-111<0-корней нет.
22.
№1. х2=t,t>0.t2+5t-6=0
t=-6-не подх.
t=1
х=1,х=-1.
х2=t,t>0.
t2-t-12=0,
t=-3-не подх.
t=4,
х=2,х=-2
23.
№2.А:х(х2-64)=0,
х=0,х=8,х=-8.
В: х2-х=t,
(t+1)(t-7)=65
t2-6t-72=0
t=12, t=-6
х2-х=12, х2-х=-6,
х=4, х=-3, Д=-23<0-корней нет,
С:-4=-1*4=-4»1=-2*2
(х+4)(х2-х-1)=0
х=-4, Д=5
х2(х2-81)=0
х=0,х=9,х=-9.
х2+х=t,
(t+6)(t-4)=144
t2+2t-168=0
t=12, t=-14,
х2+х=12, х2+х=-14,
х=-4, х=3, Д=-55<0-корней нет.
6=1*6=-1*(-6)=2*3=(-2)*(-3)
(х+1)(х2-5х+6)=0,
х=-1,х=2,х=3.











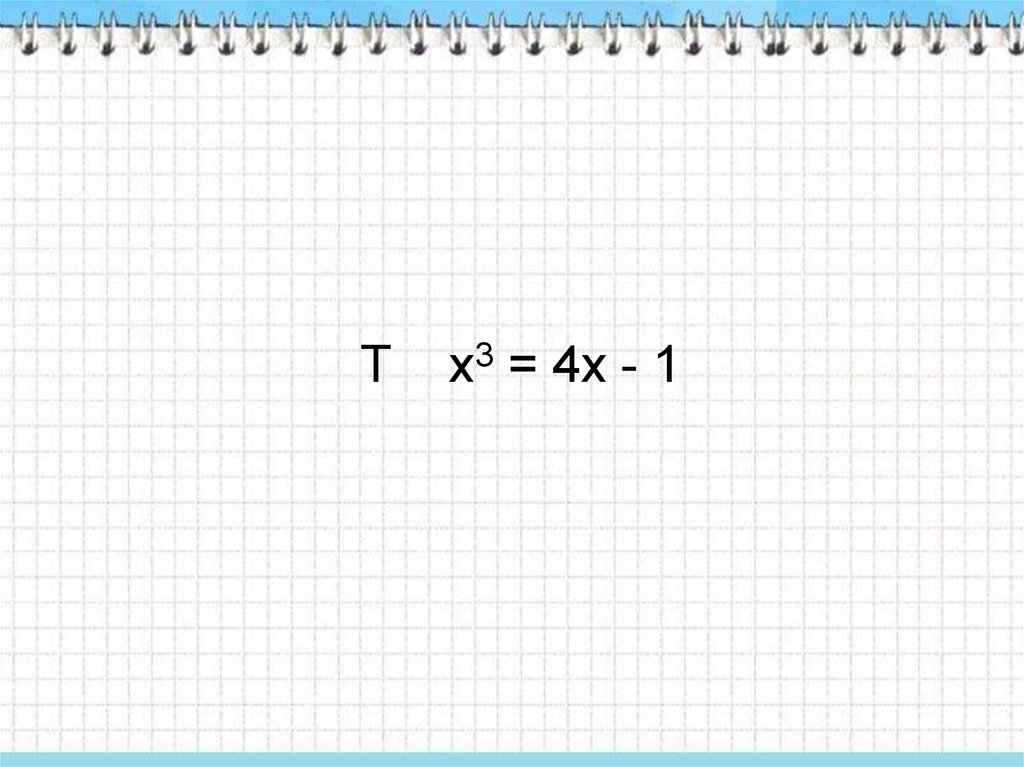

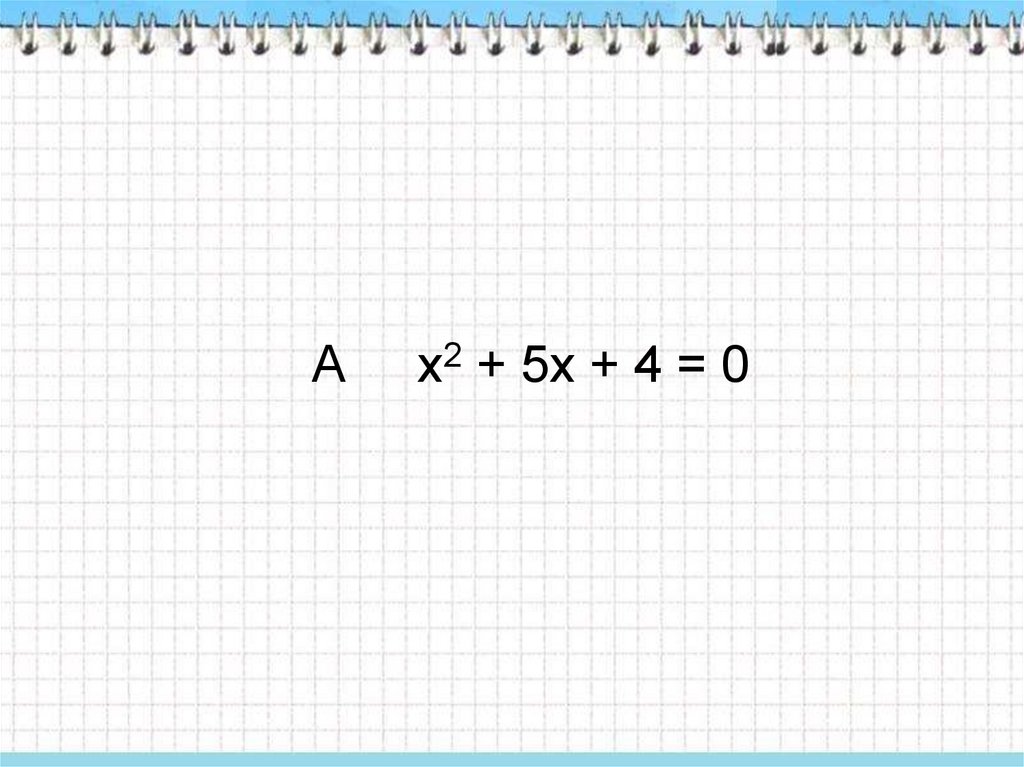










 mathematics
mathematics








