Similar presentations:
Целое уравнение и его корни. 9 класс
1.
Целое уравнение иего корни
9 КЛАСС
2. Продолжите определение:
Уравнением называется …Корнем уравнения называется…
Решить уравнение – это значит …
Какое уравнение называется целым?
3.
Целым уравнением с одной переменной называется уравнение,правая и левая части которого – целые выражения.
( x 5 2) 2 x 3 x10 3( x 2)
x3 ( x3 36) 2( x 8) 2
x10 4 x 5 4 x 3 x10 3x 6 0
x 6 36 x 3 2 x 16 2 0
4 x 5 x 3 3x 2 0
x 6 36 x 3 2 x 14 0
4.
4 x 5 x 3 3x 2 0x 6 36 x 3 2 x 14 0
5.
Уравнение первой степени можно привести к виду:Каждое уравнение первой степени имеет один корень.
6.
Уравнение второй степени можно привести к виду:7.
Задание №1. Найдите ошибки в решении уравнений:А)3 х 3 0
х1 1
2
х 2 1
В)4 х 2 0
х1 2
х 2 2
Б ) 4 х 100
х1 25
2
х2 25
8.
Задания №2. Соотнесите простейшие целые уравнения иответы :
А) х 3х 0
3
2
х2 1
Б)
2
12
5
3
В)9 х х 0
х2 3
Г)
3
13
1 1
1)0; ;
3 3
2) 6;6
3) 5;5
4)0;3
9.
Уравнение третьей степени можно привести к виду:Уравнение третьей степени имеет не более трех
корней.
Уравнение четвертой степени можно привести к виду:
Уравнение четвертой степени имеет не более
четырех корней.
10.
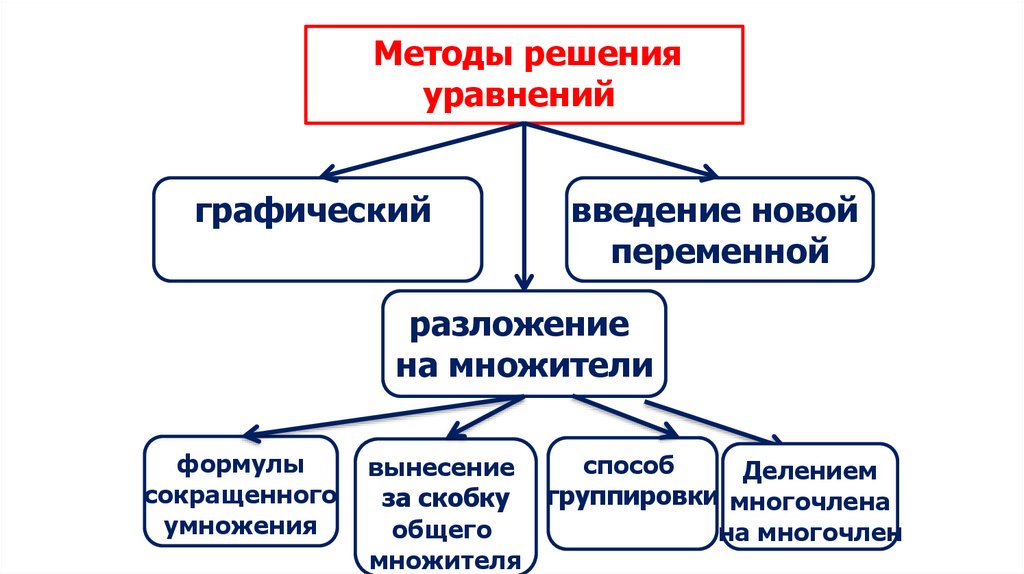
Методы решенияуравнений
графический
введение новой
переменной
разложение
на множители
формулы
сокращенного
умножения
способ
вынесение
Делением
за скобку группировки многочлена
общего
на многочлен
множителя
11.
Некоторые уравнения нетрудно решить с помощьюразложения многочлена на множители.
x 3 27 x 2 x 27 0
x 2 ( x 27) ( x 27) 0
( x 27)( x 2 1) 0
( x 27)( x 1)( x 1) 0
x 27 0
x 27
Ответ:
x 1 0
x 1
x 1 0
x 1
12.
Уравнения, степень которых выше двух, иногда удаетсярешить с помощью введения новой переменной:
( x 2 x 1)( x 2 x 4) 2
( x 2 x 1)( x 2 x 4) 2 0
x 4 2 x 3 4 x 2 5x 2 0
x2 x y
( y 1)( y 4) 2
y 2 5y 6 0
y1 2
y2 3
x2 x 2
x2 x 2 0
x1 1
x2 2
x2 x 3
x2 x 3 0
x3 1,3 x4 2,3
Ответ: 1; -2; ≈ 1,3; ≈-2,3
13.
14.
ax 4 bx 2 c 0Чтобы решить биквадратное уравнение,
вводят новое неизвестное при помощи
равенства у = х2
Тогда исходное уравнение превращается в
квадратное ay 2 by c 0 относительно
неизвестного y.
15.
16 x 4 8 x 2 1 0x2 y
16 y 2 8 y 1 0
y 0,25
x 0,25
2
x1 0,5
x2 0,5
Ответ: 0,5; –0,5.
16.
Устно. Какую подстановку необходимовыполнить, чтобы уравнение стало
квадратным?
а) х4 +2х2 + 1 = 0;
б) х6 – 3х3 + 2 = 0;
в) у8 – 4 = 0.
17.
Задание №8. Решите уравнение1 вариант
4 х 13х 3 0
2 вариант
х 4 10 х 2 25 0
4
2
18.
1 вариант2 вариант
x1 3
x2 3
Корней нет
1
x3
2
1
x4
2
19.
Замечание 1Решить уравнение
x 0
4
Имеет один корень
x 0.
Ответ: x 0.
Решить уравнение
x4 x2 0
Решение:
x4 x2 0
x 2 x 2 1 0
x 2 x 1 x 1 0
x1 0; x2 1; x3 1.
Ответ: -1; 0; 1.
20.
Замечание 2Из рассмотренных примеров видно,
что биквадратное уравнение может иметь
четыре, три, два, один действительный корень,
но может и не иметь корней.
21.
Задание. Установите соответствие:уравнение → способ
1
x x 6x 0
5
А. графический способ
3
x 6x 8 0
Б. разложение на множители
способом вынесения общего
множителя за скобки
3
В. Ввести новую переменную, т.е.
подстановку: t=…
2
4
2
x 3x 4 x 12 0
3
2
4 3
x 2 x 3x 0
5
2
x 2x 2
3
Г. Разложение на множители
способом группировки
Д. Разложение на множители
способом вынесения общего
множителя за скобки, введением
подстановки: t=…




















 mathematics
mathematics