Корни уравнения и знак коэффициента

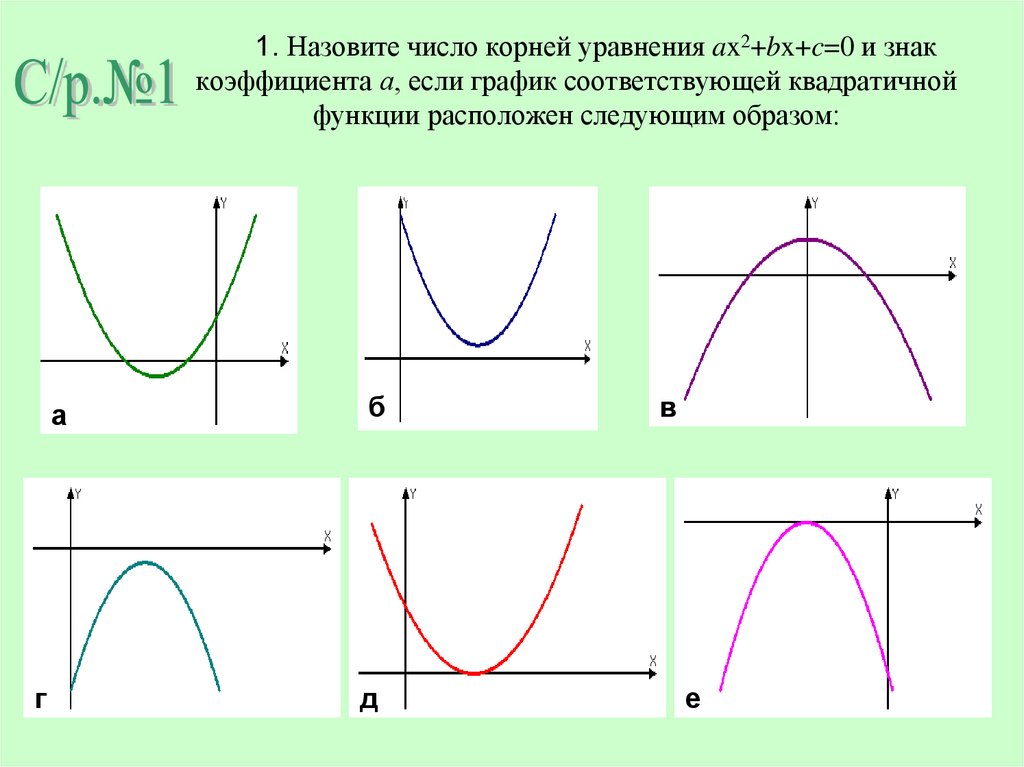
1. 1. Назовите число корней уравнения ax2+bx+c=0 и знак коэффициента а, если график соответствующей квадратичной функции

расположен следующим образом:
а
г
б
д
в
е

2.

2.Найдите корни квадратного трехчлена:
Ι вариант.
а) х2+х-12
б) х2+6х+9.
ΙΙ вариант.
а) 2х2-7х+5;
б) 4х2-4х+1.

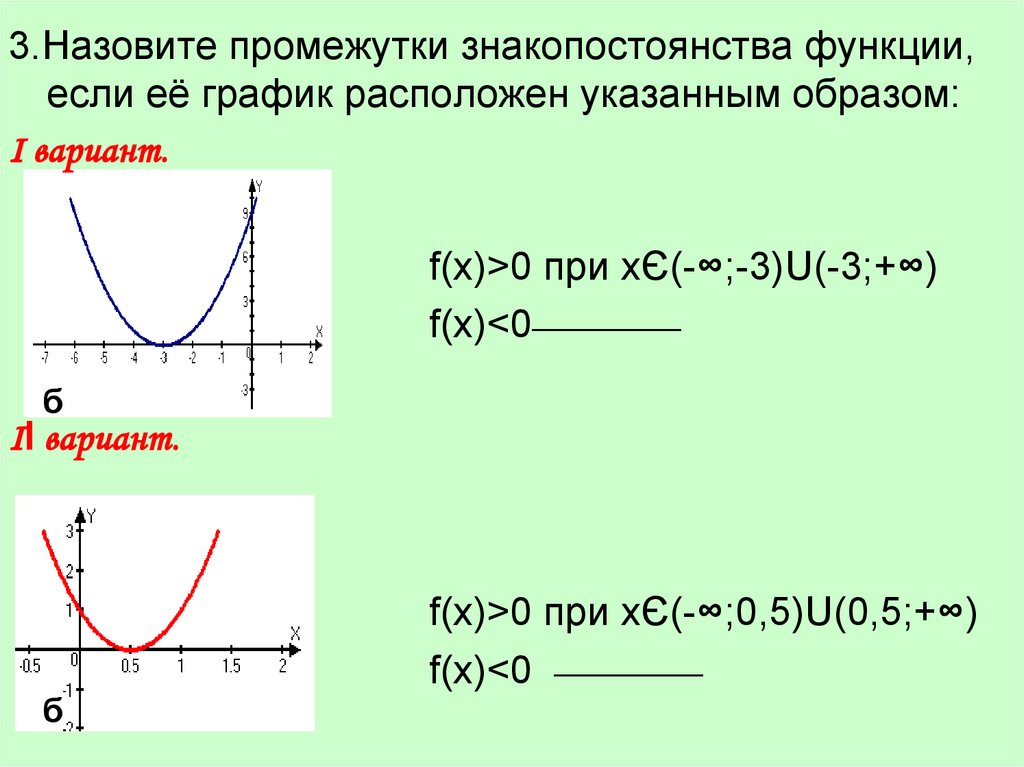
3.

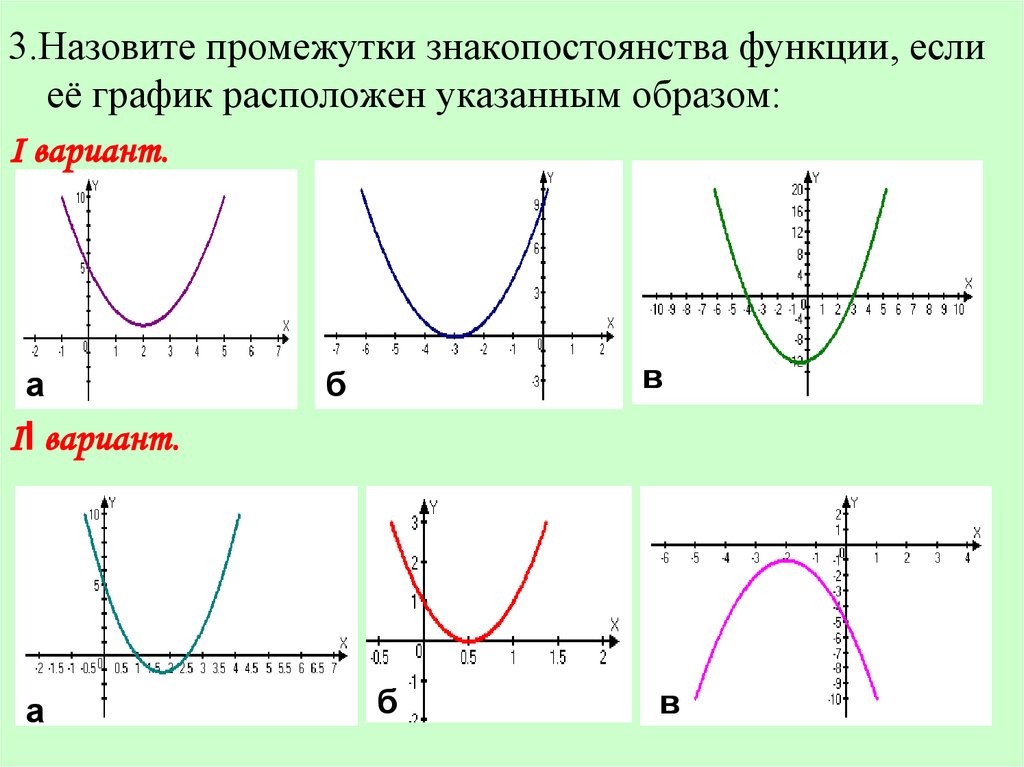
3.Назовите промежутки знакопостоянства функции, если
её график расположен указанным образом:
Ι вариант.
а
в
б
ΙІ вариант.
а
б
в

4.

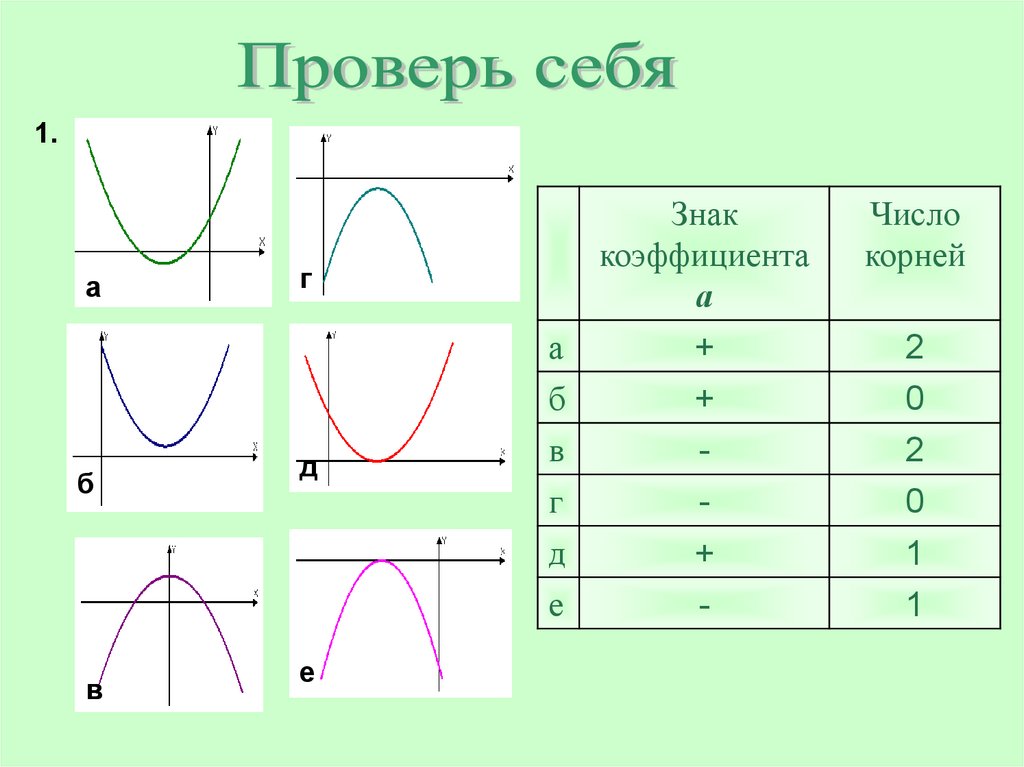
1.
а
б
в
Знак
коэффициента
а
Число
корней
а
б
+
+
2
0
в
г
-
2
0
д
е
+
-
1
1
г
д
е

5.

2.Найдите корни квадратного трехчлена:
Ι вариант.
а) х2+х-12;
б) х2+6х+9;
ΙΙ вариант.
x1=-4; x2=3
x1,2=-3
а) 2х2-7х+5;
б) 4х2-4х+1;
x1=1; x2=2,5
x1,2=0,5

6.

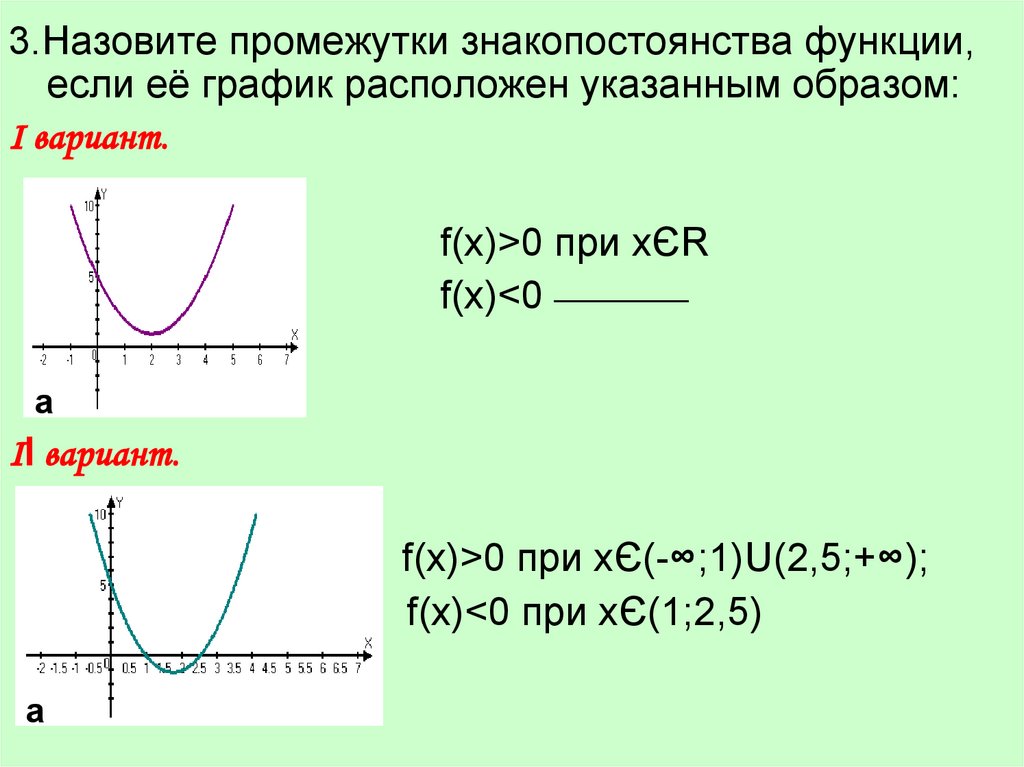
3.Назовите промежутки знакопостоянства функции,
если её график расположен указанным образом:
Ι вариант.
f(x)>0 при xЄR
f(x)<0 _________
а
ΙІ вариант.
f(x)>0 при xЄ(-∞;1)U(2,5;+∞);
f(x)<0 при xЄ(1;2,5)
а

7.

3.Назовите промежутки знакопостоянства функции,
если её график расположен указанным образом:
Ι вариант.
f(x)>0 при xЄ(-∞;-3)U(-3;+∞)
f(x)<0__________
б
ΙІ вариант.
б
f(x)>0 при xЄ(-∞;0,5)U(0,5;+∞)
f(x)<0 __________

8.

3.Назовите промежутки знакопостоянства функции,
если её график расположен указанным образом:
Ι вариант.
в
f(x)>0 при xЄ(-∞;-4)U(3;+∞);
f(x)<0 при xЄ(-4;3)
ΙІ вариант.
f(x)>0__________;
f(x)<0 при xЄR
в

9.

Являются ли следующие неравенства неравенствами второй
степени с одной переменной?
2x2 4x 6
a)
0;
2
г )4 y 2 5 y 7 0;
б )4 x 2 x 0;
д)5x 6 x 4 0;
в )2 x 4 0;
е)3 y 5 y 2 7 0.
2
2

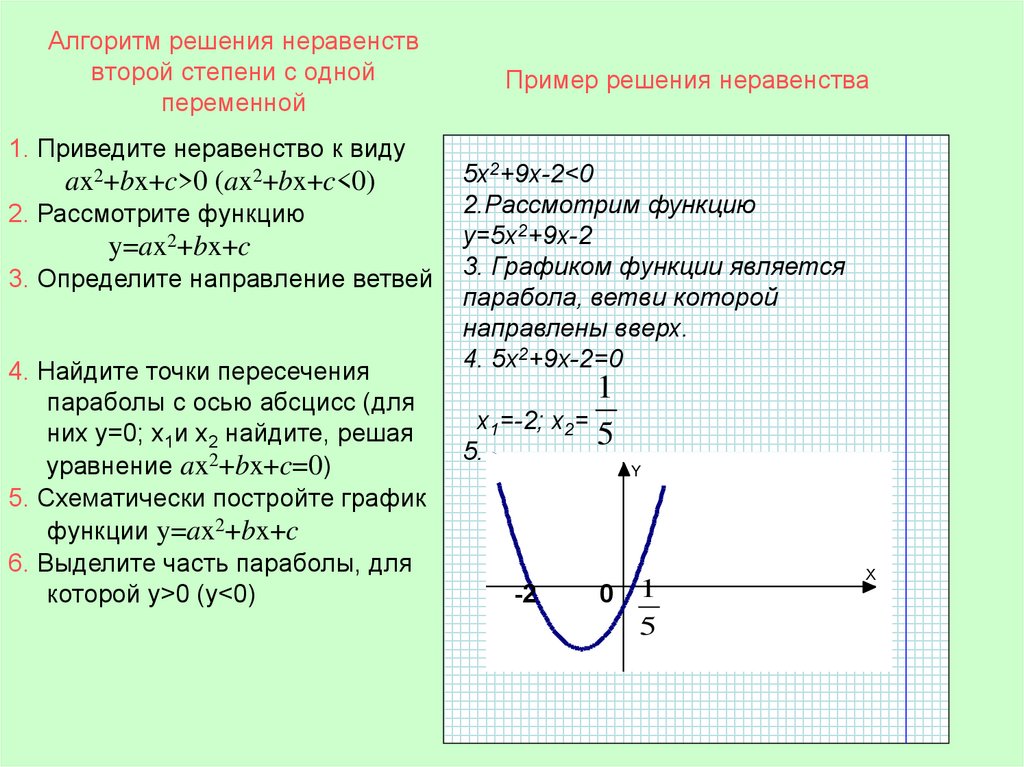
10. Алгоритм решения неравенств второй степени с одной переменной

1. Приведите неравенство к виду
ax2+bx+c>0 (ax2+bx+c<0)
2. Рассмотрите функцию
y=ax2+bx+c
3. Определите направление ветвей
4. Найдите точки пересечения
параболы с осью абсцисс (для
них y=0; х1и х2 найдите, решая
уравнение ax2+bx+c=0)
5. Схематически постройте график
функции y=ax2+bx+c
6. Выделите часть параболы, для
которой y>0 (y<0)
Пример решения неравенства
5х2+9х-2<0
2.Рассмотрим функцию
y=5х2+9х-2
3. Графиком функции является
парабола, ветви которой
направлены вверх.
4. 5х2+9х-2=0
1
х1=-2; х2=
5
5.
Y
-2
0 1
5
X

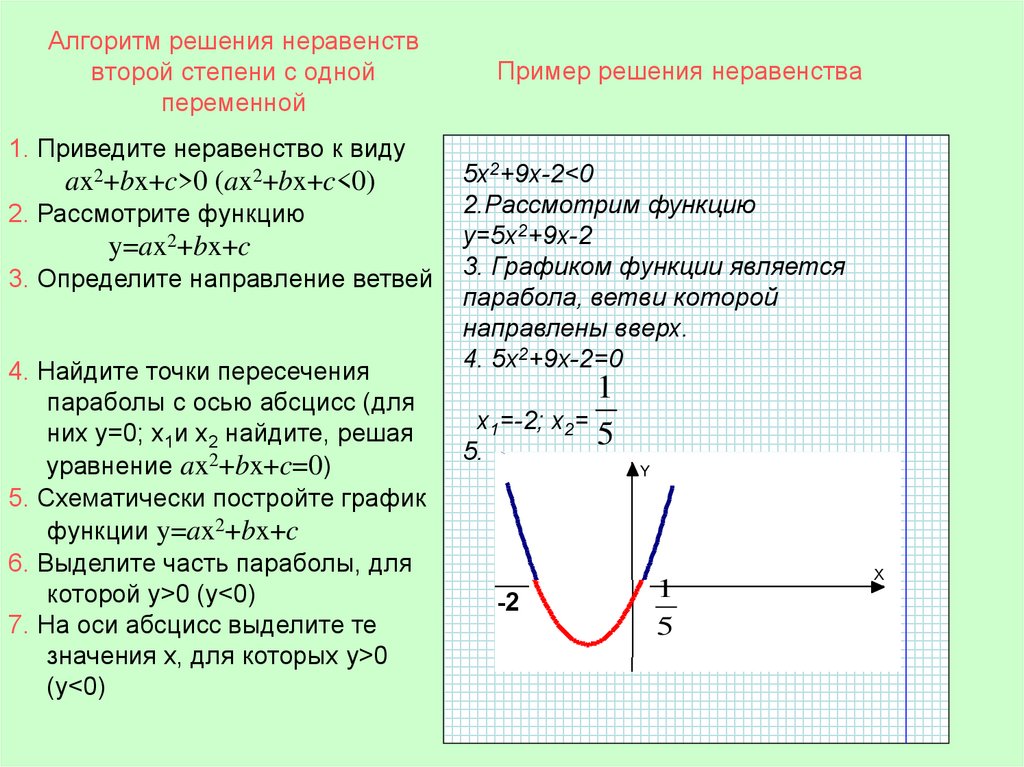
11. Алгоритм решения неравенств второй степени с одной переменной

1. Приведите неравенство к виду
ax2+bx+c>0 (ax2+bx+c<0)
2. Рассмотрите функцию
y=ax2+bx+c
3. Определите направление ветвей
4. Найдите точки пересечения
параболы с осью абсцисс (для
них y=0; х1и х2 найдите, решая
уравнение ax2+bx+c=0)
5. Схематически постройте график
функции y=ax2+bx+c
6. Выделите часть параболы, для
которой y>0 (y<0)
7. На оси абсцисс выделите те
значения х, для которых y>0
(y<0)
Пример решения неравенства
5х2+9х-2<0
2.Рассмотрим функцию
y=5х2+9х-2
3. Графиком функции является
парабола, ветви которой
направлены вверх.
4. 5х2+9х-2=0
1
х1=-2; х2=
5
5.
Y
Y
-2
0
1
5
X
X

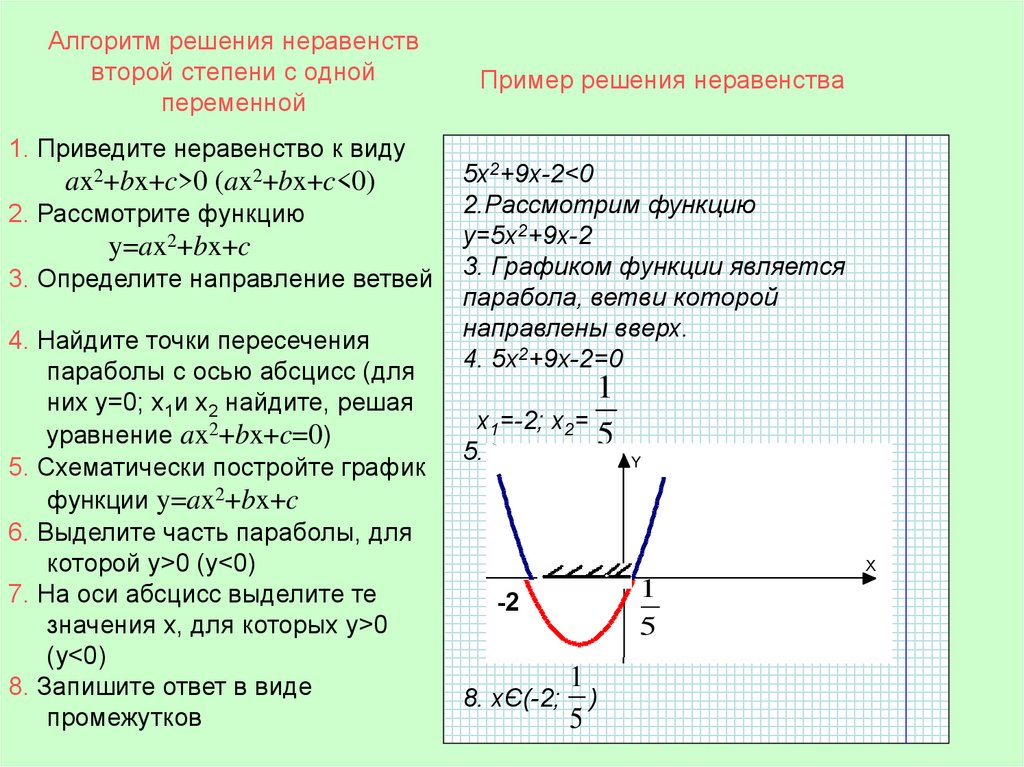
12. Алгоритм решения неравенств второй степени с одной переменной

1. Приведите неравенство к виду
ax2+bx+c>0 (ax2+bx+c<0)
2. Рассмотрите функцию
y=ax2+bx+c
3. Определите направление ветвей
4. Найдите точки пересечения
параболы с осью абсцисс (для
них y=0; х1и х2 найдите, решая
уравнение ax2+bx+c=0)
5. Схематически постройте график
функции y=ax2+bx+c
6. Выделите часть параболы, для
которой y>0 (y<0)
7. На оси абсцисс выделите те
значения х, для которых y>0
(y<0)
8. Запишите ответ в виде
промежутков
Пример решения неравенства
5х2+9х-2<0
2.Рассмотрим функцию
y=5х2+9х-2
3. Графиком функции является
парабола, ветви которой
направлены вверх.
4. 5х2+9х-2=0
1
х1=-2; х2=
5
5.
Y
Y
X X
-2
1
8. хЄ(-2; )
5
0 1
5

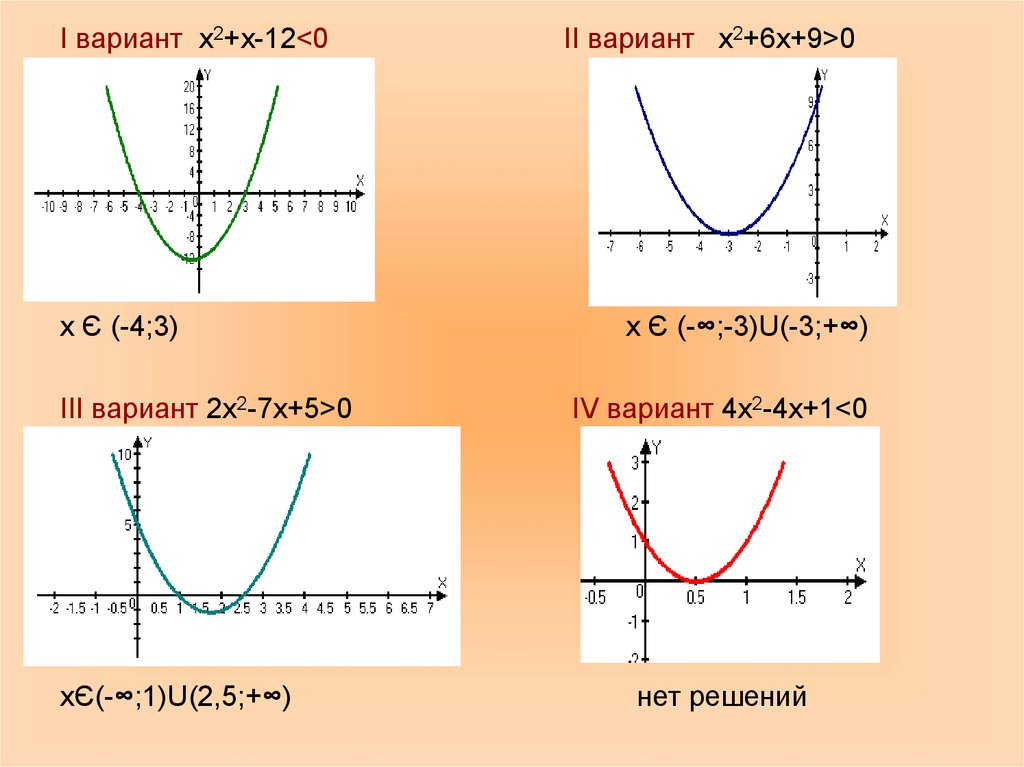
13.

Ι вариант х2+х-12<0
х Є (-4;3)
ΙΙΙ вариант 2х2-7х+5>0
хЄ(-∞;1)U(2,5;+∞)
ΙΙ вариант х2+6х+9>0
х Є (-∞;-3)U(-3;+∞)
ΙV вариант 4х2-4х+1<0
нет решений

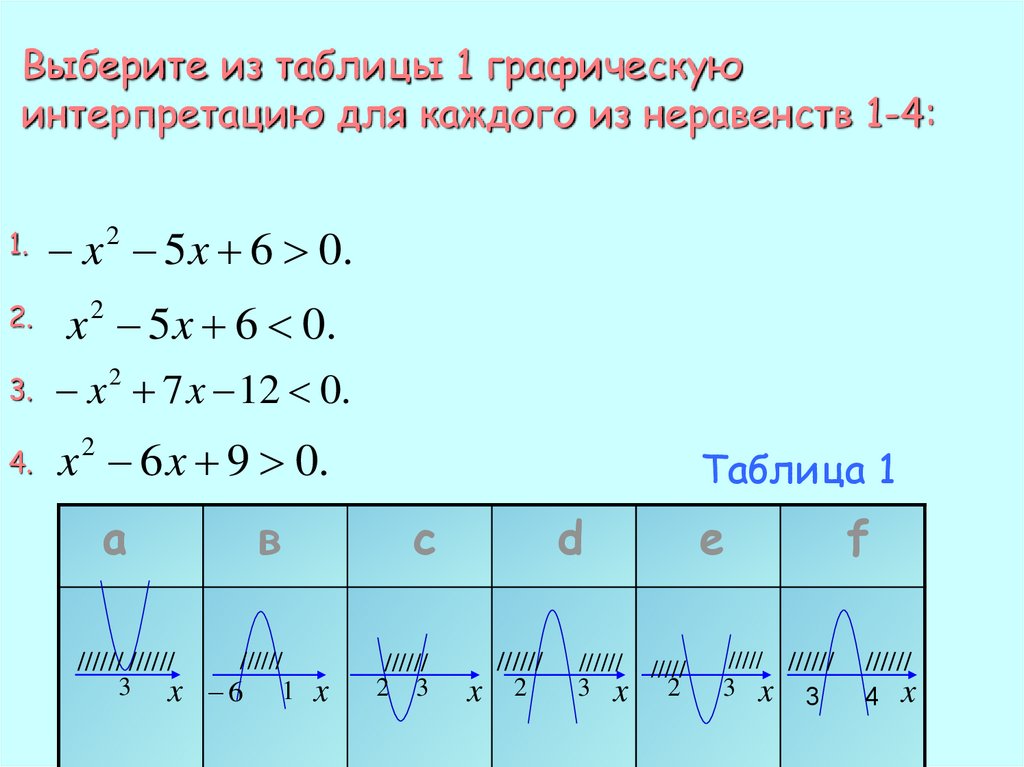
14.

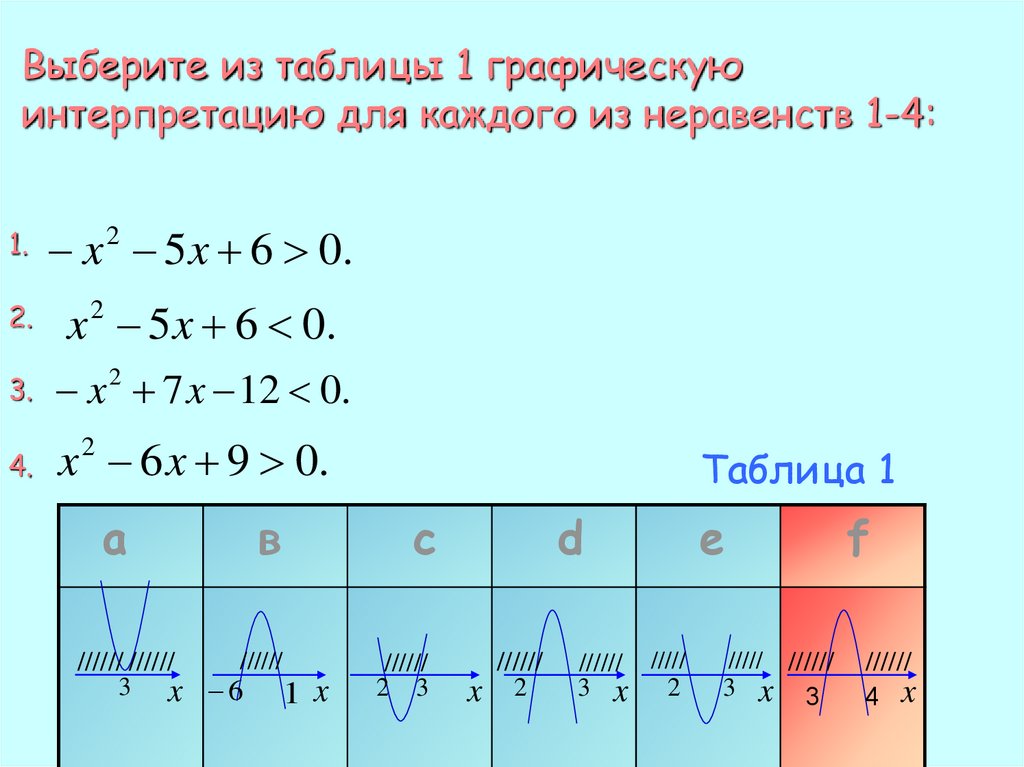
Выберите из таблицы 1 графическую
интерпретацию для каждого из неравенств 1-4:
1.
x 2 5 x 6 0.
2.
x 2 5 x 6 0.
3.
x 2 7 x 12 0.
4.
x 2 6 x 9 0.
а
в
//////
////// //////
3 x 6
1
Таблица 1
с
x
//////
2 3
d
x
//////
2
////// /////
3 x
2
e
///// //////
3 x 3
f
//////
4 x

15.

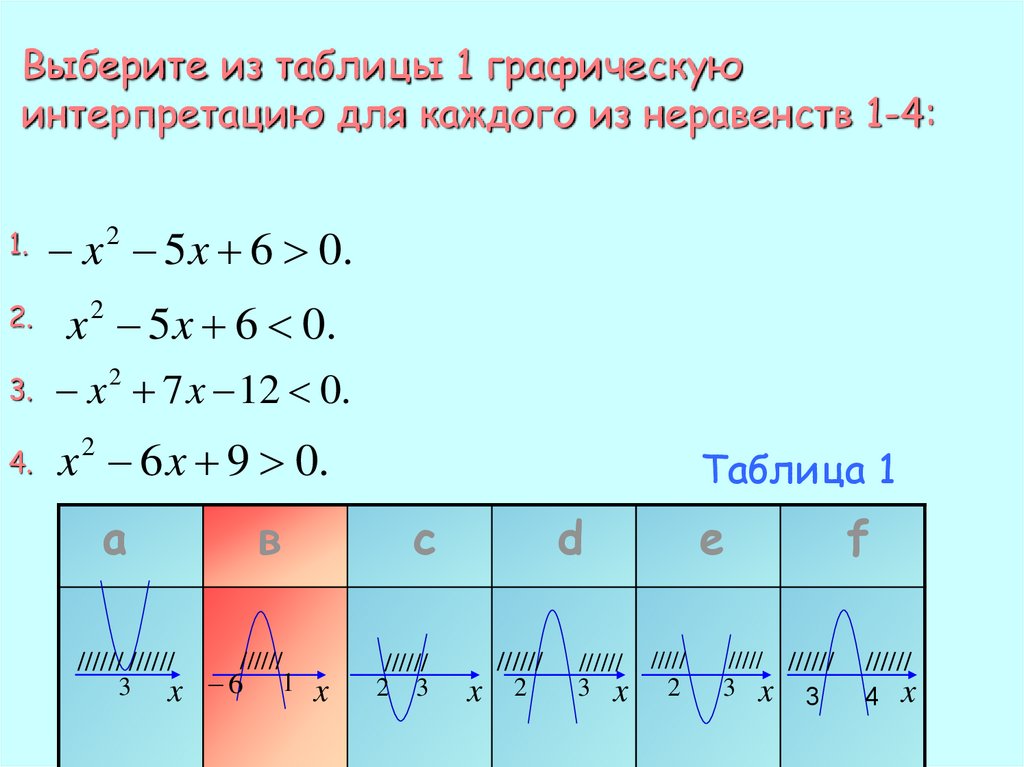
Выберите из таблицы 1 графическую
интерпретацию для каждого из неравенств 1-4:
1.
x 2 5 x 6 0.
2.
x 2 5 x 6 0.
3.
x 2 7 x 12 0.
4.
x 2 6 x 9 0.
а
в
//////
////// //////
1
3 x 6
Таблица 1
с
x
//////
2 3
d
x
//////
2
////// /////
3 x
2
e
///// //////
3 x 3
f
//////
4 x

16.

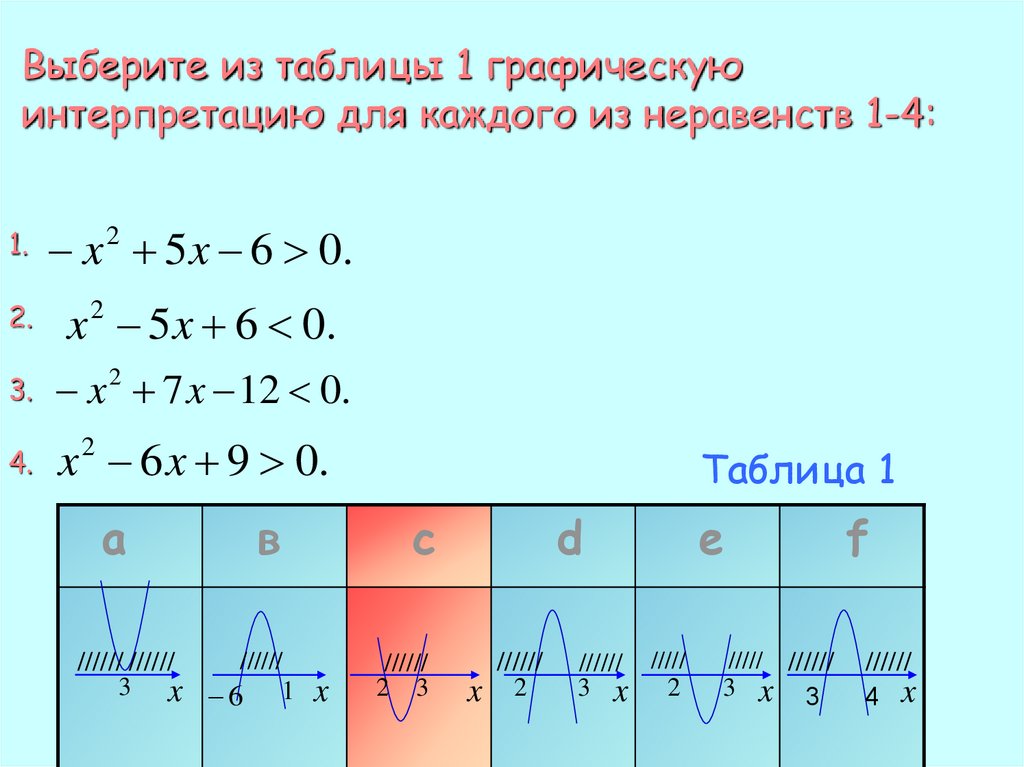
Выберите из таблицы 1 графическую
интерпретацию для каждого из неравенств 1-4:
1.
x 2 5 x 6 0.
2.
x 2 5 x 6 0.
3.
x 2 7 x 12 0.
4.
x 2 6 x 9 0.
а
в
//////
////// //////
3 x 6
1
Таблица 1
с
x
//////
2 3
d
x
//////
2
////// /////
3 x
2
e
///// //////
3 x 3
f
//////
4 x

17.

Выберите из таблицы 1 графическую
интерпретацию для каждого из неравенств 1-4:
1.
x 2 5 x 6 0.
2.
x 2 5 x 6 0.
3.
x 2 7 x 12 0.
4.
x 2 6 x 9 0.
а
в
//////
////// //////
3 x 6
1
Таблица 1
с
x
//////
2 3
d
x
//////
2
////// /////
3 x
2
e
///// //////
3 x 3
f
//////
4 x

18.

Выберите из таблицы 1 графическую
интерпретацию для каждого из неравенств 1-4:
1.
x 2 5 x 6 0.
2.
x 2 5 x 6 0.
3.
x 2 7 x 12 0.
4.
x 2 6 x 9 0.
а
в
//////
////// //////
3 x 6
1
Таблица 1
с
x
//////
2 3
d
x
//////
2
////// /////
3 x 2
e
///// //////
3 x 3
f
//////
4 x

19.

В таблице 2 найдите верное решение неравенства
1, в таблице 3 - решение неравенства 2:
1.
x 3x 4 0
2
x 3x 10 0.
2.
2
Таблица 2
а
в
x 1;4 x ; 1 4;
с
d
x 1;4 x ; 1 4;
Таблица 3
а
в
x 2;5 x ; 2 5;
с
d
x 2;5 x ; 2 5;

20.

В таблице 2 найдите верное решение неравенства
1, в таблице 3- решение неравенства 2:
1.
x 3x 4 0
2
x 3x 10 0.
2.
2
Таблица 2
а
в
x 1;4 x ; 1 4;
с
d
x 1;4 x ; 1 4;
Таблица 3
а
в
x 2;5 x ; 2 5;
с
d
x 2;5 x ; 2 5;

21.

В таблице 2 найдите верное решение неравенства
1, в таблице 3- решение неравенства 2:
1.
x 3x 4 0
2
x 3x 10 0.
2.
2
Таблица 2
а
в
x 1;4 x ; 1 4;
с
d
x 1;4 x ; 1 4;
Таблица 3
а
в
x 2;5 x ; 2 5;
с
d
x 2;5 x ; 2 5;

22.

п.14 стр.83-85.
№ 305
Составить схему для решения неравенств
2
2
ах вх с 0 , ax bx c 0 при а<0