Similar presentations:
Введение в анализ. Числовые множества. Числовые промежутки
1.
Тема 3. Введение в анализ.§3.1. Числовые множества. Числовые промежутки.
Определение: Множества, элементами которых являются числа,
называются числовыми.
Примеры числовых множеств:
Множество натуральных чисел N 1, 2, 3,..., n,...
Множество целых чисел Z 0, 1, 2, 3,..., n,...
m
Множество рациональных чисел Q m Z , n N
n
Множество действительных чисел
Множество действительных чисел обладает следующими
свойствами:
1) оно упорядоченное – для любых различных чисел а и b либо a b ,
либо b a ;
2) оно плотное – между любыми двумя различными числами а и b
существует бесконечно много действительных чисел;
3) множество R непрерывное.
Свойства непрерывности позволяет установить взаимнооднозначное соответствие между множеством действительных чисел и
множеством всех точек прямой. То есть, каждому действительному
числу соответствует единственная точка числовой оси, и наоборот,
каждой точке соответствует действительное число.
На числовой прямой (значит, и в множестве действительных чисел)
можно выделить подмножества, которые будут называться числовыми
промежутками.
a; b x R a x b - отрезок (замкнутый промежуток);
a; b x R a x b - интервал (открытый промежуток);
[ a; b) x R a x b ,
отрезки;
a; x R x a , ;b x R x b - бесконечные отрезки;
( a; b] x R a x b - полуоткрытые
a; x R x a , ;b x R x b
-
1
бесконечные
интервалы.
Числа а и b называются концами промежутков. Символы +∞ и
-∞ - это не числа, это символы для обозначения бесконечного
удаления точек числовой оси от начала отсчета.
Пусть x0 – любое действительное число (точка на числовой оси).
Определение: δ – окрестностью точки x0 называется
интервал x0 , x0 . Для любых точек этой окрестности
выполняется неравенство x x0 .
Определение: δ – окрестностью точки +∞ называется
интервал ; . Для любых точек этой окрестности выполняется
неравенство x .
Определение: δ – окрестностью точки -∞ называется
интервал ; . Для любых точек этой окрестности выполняется
неравенство x .
§3.2. Понятие функции. Числовые функции. Способы
задания функций.
Понятие функции является одним из основных понятий
математического анализа. Оно связано с установлением зависимости
между множествами.
Определение: Пусть даны два непустых множества X и Y.
Соответствие f, которое каждому элементу x X , сопоставляет один
и только один элемент y Y , называется функцией.
Записывается:
Говорят, что функция f отображает множество X на множество
Y. Множество X называется областью определения функции.
D f . Множество всех
Обозначается
называется
y Y
множеством значений функции.
2.
Математический анализ изучает числовые величины и числовыефункции. Все числовые величины могут быть разделены на две большие
группы:
1) Постоянные – величины, принимающие единственное значение
(множество состоит из одного элемента);
2) Переменные – величины, которые могут принимать различные
значения из бесконечного или конечного множества.
Можно дать другое определение для числовой функции:
переменная величина y называется функцией переменной величины x,
если по некоторому правилу или закону каждому значению переменной
x поставлено в соответствие одно определенное значение переменной y.
Переменная x называется независимой переменной или
аргументом функции. Переменная y –- зависимой переменной или
значением функции.
Способы задания функций.
1) Графический – функция задается с помощью графика. Графиком
функции называется множество точек плоскости ХОY, для каждой из
которых х – значение аргумента, y – значение функции.
2) Табличный – функция задается таблицей значений аргумента и
соответствующих им значений функции.
3) Аналитический – функция задается с помощью формулы или
совокупности формул.
Например:
Множество значений независимой переменной – это область
определения функции. Если она не указана, то под ней понимают
естественную область определения – множество значений переменной
х, не противоречащих смыслу алгебраического выражения.
При нахождении области определения нужно учитывать
следующие правила:
1) если в выражении для функции имеется корень четной степени,
то подкоренное выражение должно быть неотрицательным;
2) если в выражении для функции имеется дробь, то ее знаменатель
не должен быть равен нулю;
2
3) остальные ограничения зависят от областей определения
основных элементарных функций, входящих в состав функции.
Пример. Найти области определения следующих функций:
y 2x 3 4 x .
§3.3. Виды функций.
1) Четные и нечетные функции.
Функция y = f(x) называется четной, если для любого х из
области определения выполняется равенство f x f x .
Функция y = f(x) называется нечетной, если для любого х из
области определения выполняется равенство f x f x .
Четные и нечетные функции называются симметричными.
Большое количество функций не являются четными или нечетными
(несимметричными).
2) Возрастающие, убывающие функции (монотонные).
3) Периодические функции.
Функция y = f(x) называется периодической, если существует
такое число Т, что для любого х из области определения выполняется
равенство f x T f x .
4) Сложная функция.
Если переменная y зависит от переменной u, а переменная u
зависит в свою очередь от переменной x, то переменная y будет также
зависеть от переменной x и называться сложной функцией
переменной x.
y y u
y y u x
u u x
Говорят, что сложная функция образуется в результате
суперпозиции (наложения) функций. Переменная u является в
данном случае промежуточным аргументом: для внешней функции
это аргумент, для внутренней – значение функции.
3.
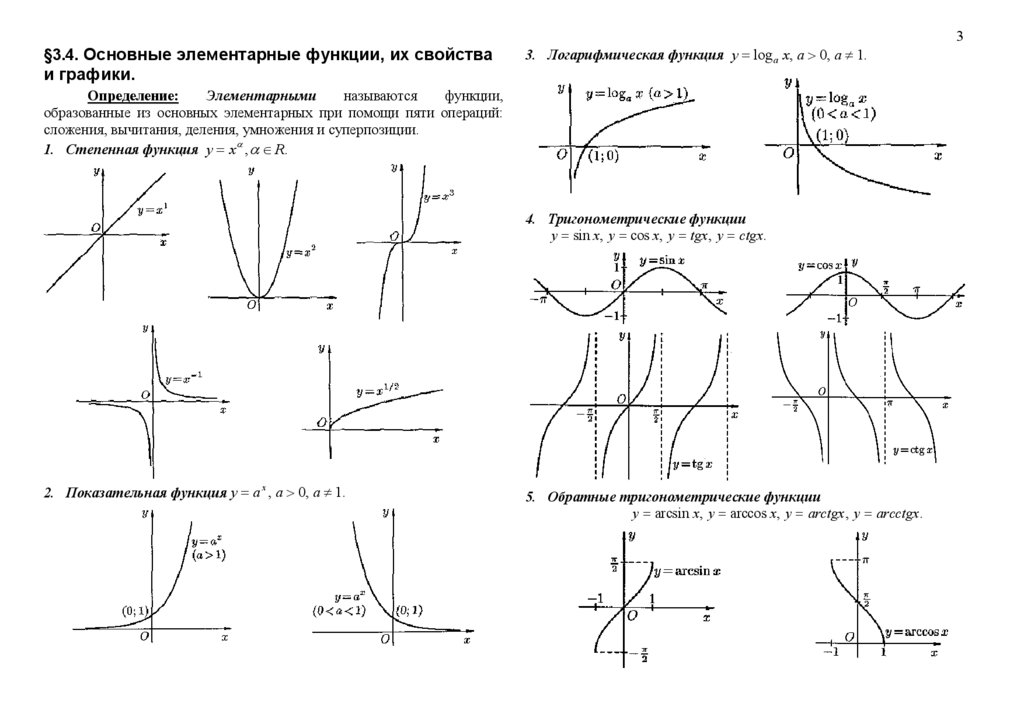
§3.4. Основные элементарные функции, их свойстваи графики.
3. Логарифмическая функция y log a x, a 0, a 1.
Определение:
Элементарными
называются
функции,
образованные из основных элементарных при помощи пяти операций:
сложения, вычитания, деления, умножения и суперпозиции.
1. Степенная функция y x , R.
4. Тригонометрические функции
y sin x, y cos x, y tgx , y ctgx.
2. Показательная функция y a x , a 0, a 1.
5. Обратные тригонометрические функции
y arcsin x, y arccos x, y arctgx , y arcctgx .
3
4.
4lim C C.
x x0
2. Предел суммы (разности) функций равен сумме (разности)
пределов этих функций:
lim( f ( x ) g ( x )) lim f ( x ) lim g ( x ).
x x0
x x0
x x0
3. Предел произведения функций равен произведению их
пределов:
lim( f ( x ) g ( x)) lim f ( x ) lim g ( x ).
x x0
Тема 4. Предел и непрерывность функции.
x x0
lim(C f ( x )) C lim f ( x ) , где С const.
x x0
§4.1. Определение предела функции.
Пусть функция y f x определена в некоторой окрестности
точки х0, кроме, может быть самой точки х0.
Определение (Коши): Число А называется пределом функции в
точке х0, если для любого положительного ε найдется такое
положительное число δ, что при всех х≠х0, удовлетворяющих
неравенству x x0 , выполняется неравенство f x A .
lim f x A .
x x0
Геометрический смысл предела
функции:
Для любой ε-окрестности точки
А найдется такая δ-окрестность
точки х0, что для всех х≠ х0 из
этой
δ-окрестности
соответствующие
значения
функции f(х) лежат в εокрестности точки А.
§4.2. Свойства пределов.
Пусть функции f (x) и g (x) определены в некоторой окрестности
точки х0 и их пределы в этой точке существуют и конечны, тогда
справедливы следующие свойства:
1. Предел постоянной равен самой постоянной:
x x0
Из свойств 3 и 1 следует, что постоянный множитель можно
выносить за знак предела, т.е.
x x0
4. Предел частного функций равен частному их пределов,
если предел знаменателя отличен от нуля:
f ( x)
f ( x ) xlim
x0
, если lim g ( x ) 0.
x x0
x x0 g ( x )
lim g ( x )
lim
x x0
5. Если предел функции существует, то он единственный.
§4.3. Непрерывность функции.
Пусть функция у=f(х) определена в точке х0 и в некоторой
окрестности этой точки.
Определение 1: Функция у=f(х) называется непрерывной в
точке х0, если существует предел функции в этой точке и он
равен значению функции в этой точке.
lim f x f x 0
x x0
Данное равенство означает выполнения трех условий:
1. функция f(х) определена в точке х0 и в ее окрестности;
2. функция f(х) имеет предел при x x0 ;
3. предел функции в точке х0 равен значению функции в этой точке.
lim x x 0 lim f x f lim x f x 0
x x0
x x0
x x0
При нахождении предела непрерывной функции f(х) можно
перейти к пределу под знаком функции, т.е. в функцию f(х) вместо
аргумента х подставить его предельное значение х0.
Пример: Вычислить предел, используя непрерывность функции
5.
x 4x 1 5 3 x
2
lim
Определение: Функция у=f(х) называется непрерывной в
интервале (a;b), если она непрерывна в каждой точке этого
интервала.
Все элементарные функции непрерывны в своей области
определения, поэтому для нахождения предела элементарной функции в
точке х0 достаточно вычислить значение функции в этой точке.
§4.4. Бесконечно большие и бесконечно малые функции.
Определение: Функция y f x называется бесконечно
большой при x x0 , если для любого числа M>0 существует число
δ=δ(М)>0, что для всех х, удовлетворяющих неравенству
0 x x0 , выполняется неравенство f x M .
lim f x
x x0
1
есть ббф при x 2 .
x 2
Определение: Функция y f x , заданная на всей числовой
прямой, называется бесконечно большой при x , если для любого
числа M>0 найдется такое число N=N(M)>0, что при всех х,
удовлетворяющих неравенству x N , выполняется неравенство
Например, y
f x M .
Например, y 2 x есть ббф при x .
Определение: Функция y f x называется бесконечно малой
при x x0 , если
lim f x 0 .
x x0
Бесконечно малые функции называют бесконечно малыми
величинами и обозначают α, β и т.д.
5
Свойства бесконечно малых функций:
1) Алгебраическая сумма конечного числа бесконечно малых
функций есть бесконечно малая функция.
2) Произведение ограниченной функции на бесконечно малую
функцию есть бесконечно малая функция.
3) Так как всякая бмф ограничена, то произведение двух бмф есть
функция бесконечно малая.
4) Произведение бмф на число есть бесконечно малая функция
5) Частное от деления бесконечно малой функции на функцию,
имеющую отличный от нуля предел, есть функция бесконечно малая.
1
6) Если функция α(х) – бмф (α≠0), то функция
есть
x
бесконечно большая функция и наоборот: если функция f(x) –
1
бесконечно большая функция , то
- бесконечно малая.
f x
Теорема: Если функция f(x) имеем предел, равный А, то ее
можно представить как сумму числа А и бесконечно малой функции
α(х), т.е. если lim f x A , то f x A x .
x x0
Теорема (обратная): Если функцию f(x) можно представить
в виде суммы числа А и бесконечно малой функции α(х), то число А
является пределом функции f(x), т.е. если f x A x , то
lim f x A .
x x0
§4.5. Раскрытие неопределенностей.
При вычислении пределов используются свойства пределов и
свойство непрерывности элементарных функций в области
определения. Но в ряде случаев при вычислении пределов возникают
неопределенности.
: Числитель и знаменатель
Неопределенность вида
делят на наивысшую из имеющихся степеней аргумента.
7 x4 x2
Пример 2 Вычислить lim 4
=
x 2 x x 2 5
6.
6sin x
1
x 0
x
Первый замечательный предел: lim
Следствия:
0
0
Неопределенность вида :
Для дроби:
разложить числитель и знаменатель на множители и сократить дробь на
общий множитель;
4 x2 x
Пример 3: Вычислить lim 2
x 0 3 x 2 x
x
1
x 0
sin x
arcsin x
lim
1
x 0
x
tgx
1
x 0
x
arctgx
lim
1
x 0
x
lim
lim
Следствия:
sin x
1
x
ln 1 x
1
x 0
x
ex 1
lim
1
x 0
x
1
lim 1 x x e
Пример
5:Найдите
замечательные пределы
sin 3 x
=
x 0 sin 5 x
а) lim
2
б) lim 1 3 x x =
x 0
В других случаях использовать замечательные пределы:
lim
x 0
1 cos x 1
x2
2
x
lim
a x 1
lim
ln a
x 0
x
x
Пример 4: Вычислить lim
=
x 0
2 x 2 x
x 0
1
Второй замечательный предел: lim 1 e .
x
x
x 0
При наличии иррациональности:
перевести иррациональность из числителя в знаменатель или наоборот;
lim
пределы
функций,
используя
7.
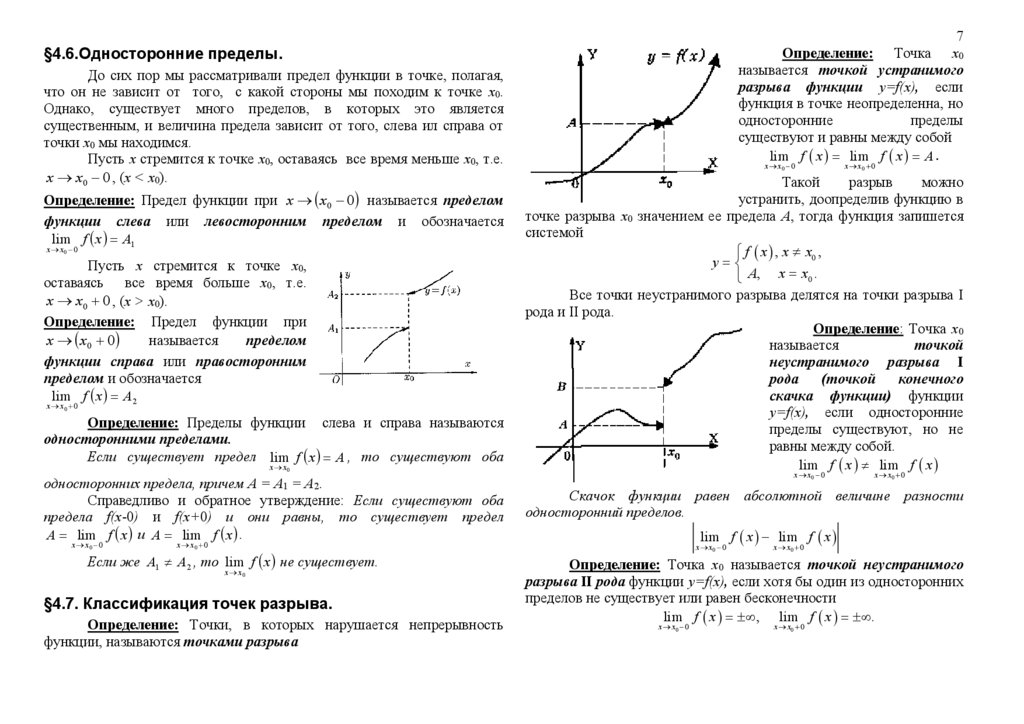
7Определение: Точка х0
называется точкой устранимого
разрыва функции y=f(x), если
функция в точке неопределенна, но
односторонние
пределы
существуют и равны между собой
lim f x lim f x A .
§4.6.Односторонние пределы.
До сих пор мы рассматривали предел функции в точке, полагая,
что он не зависит от того, с какой стороны мы походим к точке х0.
Однако, существует много пределов, в которых это является
существенным, и величина предела зависит от того, слева ил справа от
точки х0 мы находимся.
Пусть х стремится к точке х0, оставаясь все время меньше х0, т.е.
x x0 0 , (x < x0).
Определение: Предел функции при x x0 0 называется пределом
функции слева или левосторонним пределом и обозначается
lim f x A1
x x0 0
Пусть х стремится к точке х0,
оставаясь все время больше х0, т.е.
x x0 0 , (x > x0).
Определение: Предел функции при
x x 0 0
называется
пределом
функции справа или правосторонним
пределом и обозначается
lim f x A2
x x0 0
Определение: Пределы функции слева и справа называются
односторонними пределами.
Если существует предел lim f x A , то существуют оба
x x0
односторонних предела, причем А = А1 = А2.
Справедливо и обратное утверждение: Если существуют оба
предела f(х-0) и f(х+0) и они равны, то существует предел
A lim f x и A lim f x .
x x0 0
x x0 0
Такой
разрыв
можно
устранить, доопределив функцию в
точке разрыва х0 значением ее предела А, тогда функция запишется
системой
f x , x x0 ,
y
A, x x0 .
Все точки неустранимого разрыва делятся на точки разрыва I
рода и II рода.
Определение: Точка х0
называется
точкой
неустранимого разрыва I
рода
(точкой
конечного
скачка функции) функции
y=f(x), если односторонние
пределы существуют, но не
равны между собой.
lim f x lim f x
x x0 0
x x0
§4.7. Классификация точек разрыва.
Определение: Точки, в которых нарушается непрерывность
функции, называются точками разрыва
x x0 0
Скачок функции равен абсолютной величине разности
односторонний пределов.
lim f x lim f x
x x0 0
Если же A1 A2 , то lim f x не существует.
x x0 0
x x0 0
x x0 0
Определение: Точка х0 называется точкой неустранимого
разрыва II рода функции y=f(x), если хотя бы один из односторонних
пределов не существует или равен бесконечности
lim f x , lim f x .
x x0 0
x x0 0
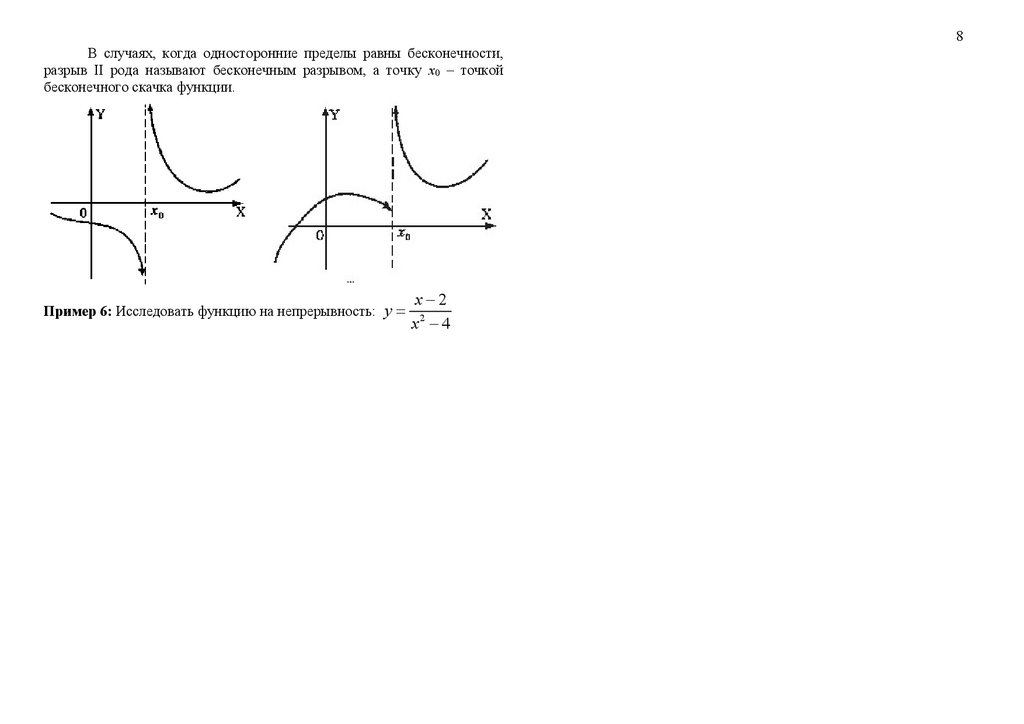
8.
8В случаях, когда односторонние пределы равны бесконечности,
разрыв II рода называют бесконечным разрывом, а точку х0 – точкой
бесконечного скачка функции.
Пример 6: Исследовать функцию на непрерывность: y
x 2
x2 4





 mathematics
mathematics








