Similar presentations:
Математический анализ. Множества. Числовые последовательности
1.
Математический анализне менее всеобъемлющ,
чем сама природа.
Ж.Фурье
Математический
анализ
Множества.
Числовые последовательности
2.
, …!
:
некоторые высказывания или утверждения, относительно
каждого из которых можно сказать – истинно оно или ложно
«не », т.е. отрицание утверждения
«из утверждения следует утверждение »; (символ
импликации)
«утверждение эквивалентно утверждению »; « и
равносильны»
«утверждение является необходимым и достаточным
условием » (символ эквивалентности)
«каково бы ни было», «любой», «каждый» (квантор
всеобщности); a A
- для любого элемента a,
принадлежащего множеству
«существует» (квантор существования); a A – существует
элемент a принадлежащий множеству А
«единственный» (символ единственности)
«такое, что», «выполняется», «удовлетворяет условию»
3. 1 Понятие множества
Множество (set) – некоторая, вполне определеннаясовокупность объектов произвольной природы, каждый
их которых называется элементом множества.
Георг Кантор (1845-1918)
Множество есть «объединение в
одно целое объектов, хорошо
различимых нашей интуицией
или мыслью».
4. Примеры множеств
5. Элементы множества (set members)
Объекты, которые образуют множество, называютсяего элементами.
Бесконечное множество содержит бесконечное
число элементов. Конечное множество состоит из
конечного числа элементов.
Пример.
Множество натуральных чисел – бесконечное
множество.
Множество студентов факультета – конечное
множество.
6. Обозначения
В дальнейшем множества будем обозначатьпрописными латинскими буквами, элементы –
строчными латинскими.
a ∈ A – «элемент a принадлежит множеству A».
a A – «элемент a не принадлежит множеству A»
7. Пустое множество (empty set, null set)
Множество, не содержащее ни одногоэлемента, называется пустым и обозначается
.
Пример.
Множество
оценок
первокурсника в первом семестре.
в
зачетке
8. Подмножество (subset)
Множество B называется подмножеством множестваA, если каждый элемент множества В является
элементом множества А.
Рис. Диаграмма Эйлера-Венна, изображающая подмножество В множества А
Пример. Множество
первокурсников есть
подмножество множества студентов.
9. Равные множества (equal sets)
Два множества А и В называются равными, если онисостоят из одних и тех же элементов.
Обозначение:
A=B
Например, A = {филателисты} и B={аквалангисты}
А=В если любой филателист является
одновременно аквалангистом и наоборот.
10. Универсальное множество (universal set)
Универсальное множество U есть совокупностьвсех рассматриваемых в задаче множеств.
Пример. Имеются два множества:
A = { 3, 7, 11, 15 }
B = { 2, 4, 6, …, 2n, … }
Множество U = { все целые числа } является
универсальным множеством для множеств A и B.
11. Числовые множества
• N ={1, 2, 3…} – множество натуральных чисел;• Z ={0, 1, 2, 3,… } – множество целых чисел ;
• Q – множество рациональных чисел вида
m
q : m Z , n N
n
• I – множество иррациональных чисел, т.е. чисел,
представимых в виде бесконечной десятичной
непериодической дроби, например 2 , e, , …;
• R – множество действительных (вещественных)
чисел, образуемое совокупностью рациональных Q
и иррациональных I чисел:
R Q I.
12. 2 Операции над множествами
2-1 Объединение (сумма)2-2 Пересечение (произведение)
2-3 Разность (вычитание)
2-4 Симметрическая разность
2-5 Дополнение
2-6 Свойства операций
13. 2-1 Объединение множеств (sum of sets)
• Объединением (суммой) двух множеств А и В называетсямножество С, состоящее из всех элементов, принадлежащих
хотя бы одному из данных множеств:
Обозначение: А + В = А В
Пример.
A = { жители Москвы } и B = { жители
Подмосковья }
С = А В = { жители Москвы или Подмосковья }
ВОПРОС:
D = { 1, 3, 5} и F = { 2, 4, 6}.
Тогда M = D F = ?
14. 2-2 Пересечение множеств (intersections of sets)
• Пересечением (произведением) двух множеств А иВ называется множество D, состоящее из всех
элементов, одновременно принадлежащих каждому
из данных множеств:
Обозначение: А·В = А В
Пример.
A = { студенты, участвовавшие в концерте }
B = { студенты 104 группы }
ЗАДАЧА
D = { студенты 104 группы, участвовавшие в концерте }
A = (0;5) и B = [4;9)
D = А В?
15. 2-3 Разность множеств (set difference)
• Разностью двух множеств А и В называетсямножество F, состоящее из всех элементов
принадлежащих множеству А, но не принадлежащих
множеству В:
Обозначение: А – В = А \ В
Пример.
ЗАДАЧА
A = [1;3] и B = N
A=RиB=I
F = А – В = (1;2) (2;3)
F=А\I=?
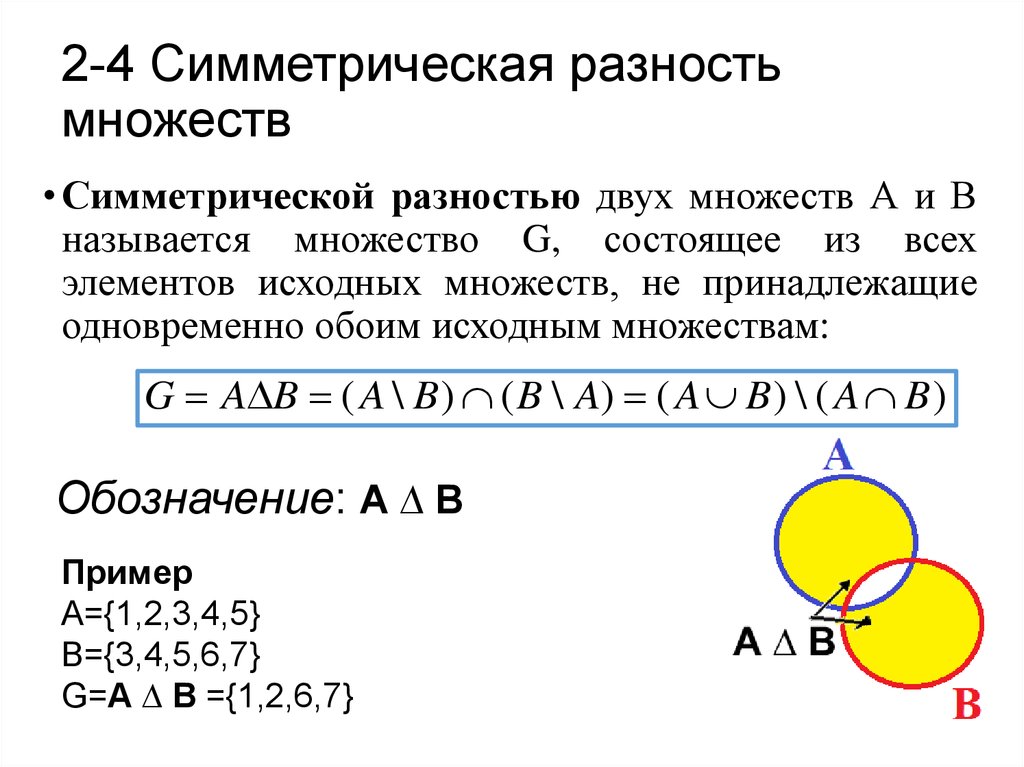
16. 2-4 Симметрическая разность множеств
• Симметрической разностью двух множеств А и Вназывается множество G, состоящее из всех
элементов исходных множеств, не принадлежащие
одновременно обоим исходным множествам:
G A B ( A \ B ) ( B \ A) ( A B ) \ ( A B )
Обозначение: А ∆ В
Пример
А={1,2,3,4,5}
B={3,4,5,6,7}
G=А ∆ В ={1,2,6,7}
17. 2-5 Дополнение к множеству (set compliment)
Дополнением к множеству A называется множествоэлементов универсального множества, не
принадлежащих A:
Ᾱ=U –A
Обозначение:
Пример.
A = { девушки 11 группы }
U = { все студенты 11 группы }
Ᾱ = { юноши 11 группы }
18. 2-6 Свойства операций над множествами
Для введенных операций присущи следующиесвойства:
19. 3 Числовые промежутки и ограниченные множества
20.
Числовые промежуткиМножество элементов x:
Элемент множества:
Отрезок (сегмент):
Интервал:
x
x x
x a, b : a x b, где
a x , b x
x a, b : a x b
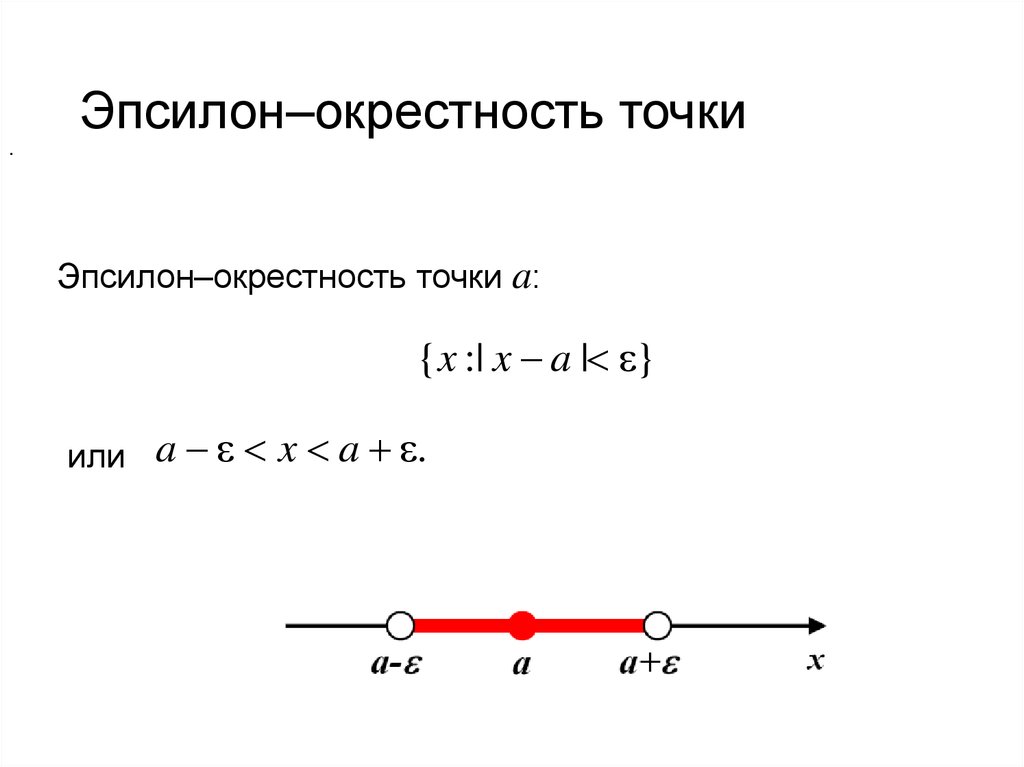
21. Окрестность точки (neighborhood of point)
Абсолютная величина разности двух чисел |x – a|означает расстояние между двумя точками х и а
числовой прямой как для случая х<а, так и для х>а.
Окрестность точки c – произвольный интервал (a,b),
содержащий точку с.
b
22. Эпсилон–окрестность точки
.Эпсилон–окрестность точки
Эпсилон–окрестность точки a:
{x :| x a | }
или a x a .
23.
Ограниченные множестваМножество
x
называется ограниченным сверху,
если существует такое число М, что
x x : x M .
Множество x называется ограниченным снизу, если
существует такое число m, что
Множество
x
x x : x m .
называется ограниченным, если
x x : m x M .
24.
Грани числовых множествЕсли множество Х ограничено сверху, то говорят, что
множество имеет верхнюю границу
b R : x X x b.
Наименьшая из верхних границ множества Х
называется точной верхней гранью и обозначается
supX.
Наибольшая из нижних границ множества Х называется
точной нижней гранью и обозначается infX.
25.
Задача.Найти точную верхнюю и точную нижнюю
грани множества [0, 1).
Решение.
1. Это множество не имеет наибольшего
элемента, так как для x [0,1) найдется
y [0,1) такой, что y x.
Множество верхних граней для данного
полуинтервала [0, 1) – это множество [1, )
с наименьшим элементом, равным 1. Отсюда
sup[0,1) 1,
причем 1 не принадлежит заданному множеству.
26.
С другой стороны, наименьший элемент длярассматриваемого множества [0,1) существует и
равен 0.
Множество нижних граней – это множество ( ;0]
с наибольшим элементом, равным 0, который и
является точной нижней гранью полуинтервала [0,1).
Таким образом,
inf[0,1) 0,
причем
0 [0,1).
Неограниченные множества: (-∞,∞), (-∞,2], [-5,∞).
ТВГ (-∞,2] равна 2, ТНГ [-5,∞) равна -5.
27. 4 Числовые последовательности
• 1 Определение последовательности• 2 Предел последовательности
• 3 Теоремы о пределах
• 4 Бесконечно большие и бесконечно
малые последовательности
• 5 Вычисление пределов
28. 4-1 Определение последовательности
Если каждому натуральномучислу n по определенному закону
поставлено в соответствие
некоторое число xn, то множество
xn x1, x2 , x3 ,....xn ,...
пронумерованных чисел x1, x2,
x3,…
называется
числовой
последовательностью.
Элементы этого множества
называются членами числовой
последовательности.
29. Примеры последовательностей
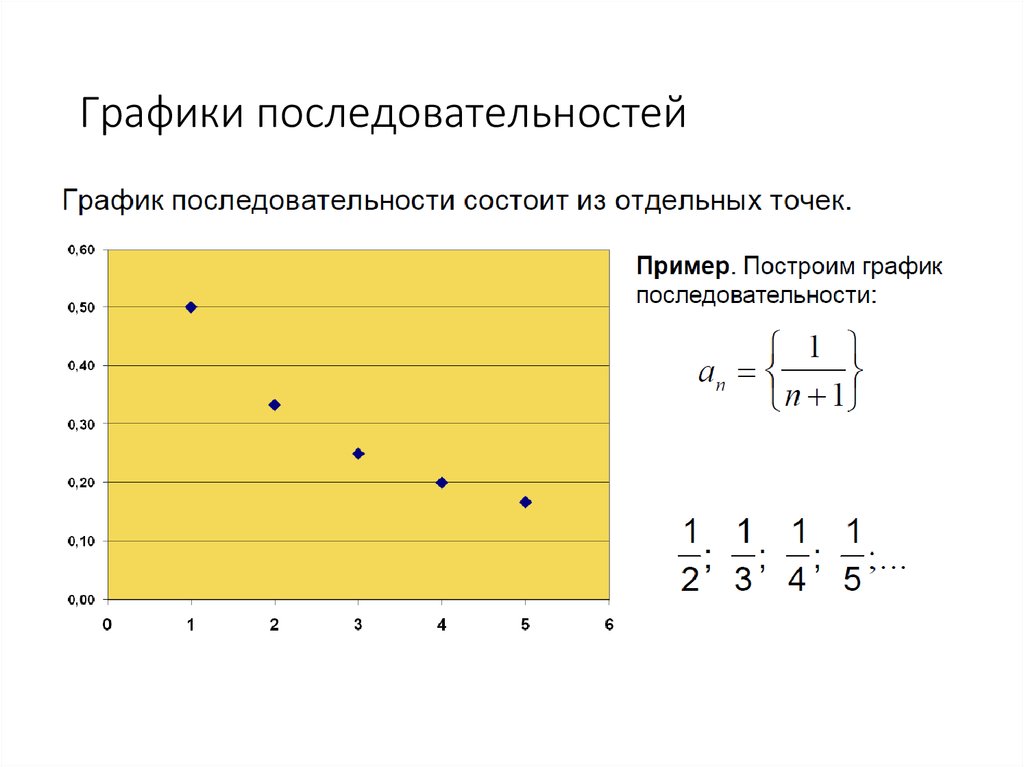
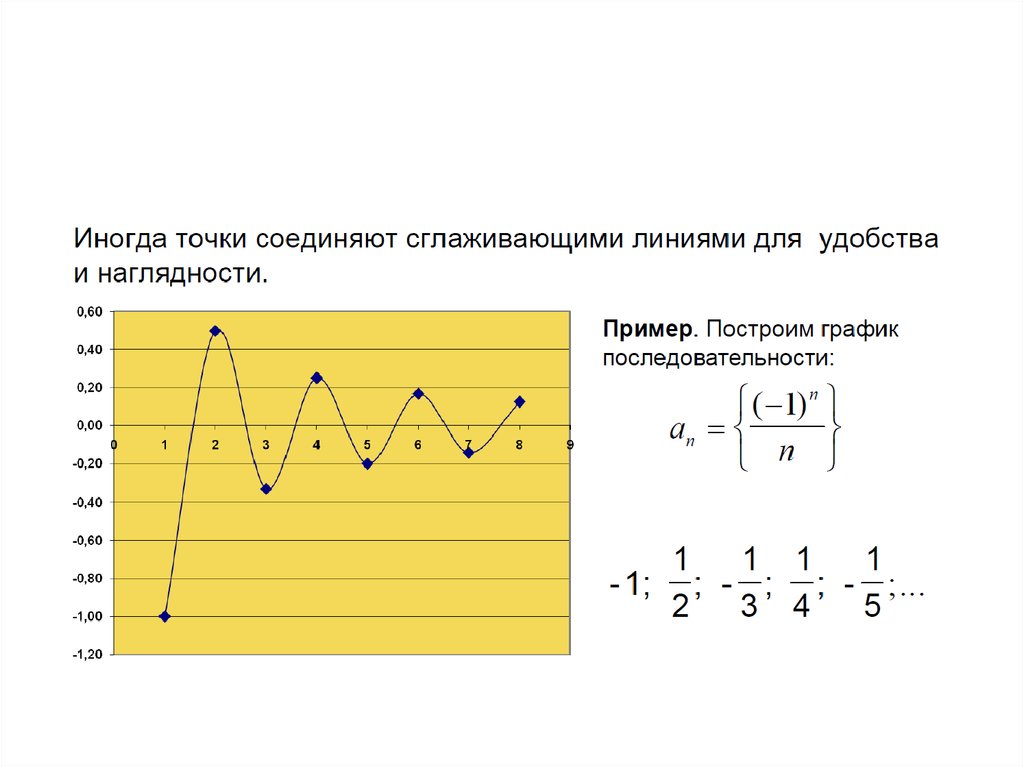
30. Графики последовательностей
31.
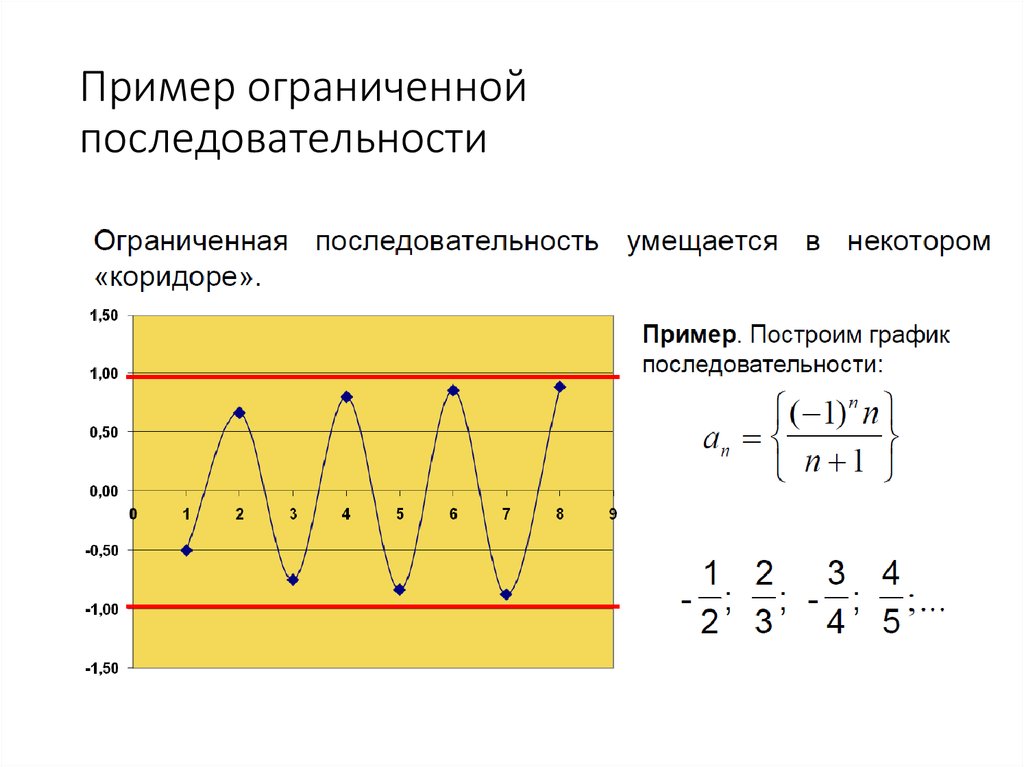
32. Ограниченная последовательность
33.
ПРИМЕРЫ1. Последовательность xn n 1, 2, 3,... n,...
ограничена сверху, поскольку все члены этой
последовательности удовлетворяют неравенству xn 1 .
2. Последовательность xn n2 1,4,9,16,..... ограничена
снизу, т.к. xn n2 1.
1
3. Последовательность xn ограничена. Для любого
n
n N 0
1
1,
n
т.е. M 1, m 0 .
34. Пример ограниченной последовательности
35.
Свойства ограниченных последовательностей1. Сумма, разность
последовательностей
последовательность.
и
произведение
дают
ограниченных
ограниченную
2. Частное двух ограниченных последовательностей может
быть как ограниченной, так и неограниченной
последовательностью.
Если
xn
1
,
n
а
yn
последовательность,
1
n2
, то
xn
n
yn
тогда
последовательность ограниченная.
как
– неограниченная
yn 1
xn n
–
36. 4-2 Предел последовательности
• Понятие последовательности• Определение предела последовательности
• Геометрический смысл
37. Предел последовательности
38. Предел числовой последовательности
Последовательность, имеющая предел, называется сходящейся, впротивном случае – расходящейся.
39. Определение предела в кванторах
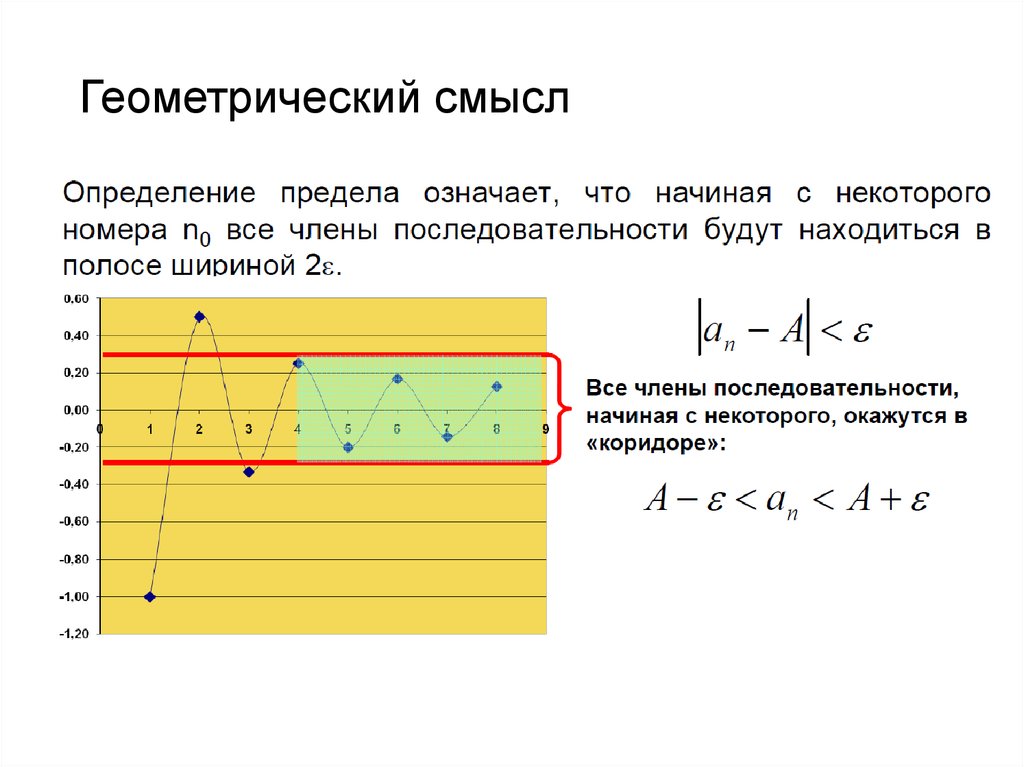
40.
Последовательность xn сходится к a ; если общийчлен последовательности xn a стремится к a и,
n
начиная с некоторого номера, все члены
последовательности попадают в эпсилон-окрестность
числа a .
Последовательность,
называется сходящейся.
имеющая
конечный
предел,
41. Геометрический смысл
42. пример 1
43. решение примера 1
44. решение примера 1(продолжение)
45.
пример 2n 1
n 1
1
x
xn lim
lim 1 1 .
Дано: n
, lim
n
n
n
n
n
n
n 1
1.
Докажем по определению, что lim
n
n
46.
Доказательство.0,
n 1
1
1
1
1 1 1 ;
, n .
n
n
n
1
N
В качестве выберем N 1,
1
где - символ целой части числа,
тогда неравенство
n 1
1 будет выполнено n N .
n
47.
Геометрическаяинтерпретация:
0
x
1
1
2
2
3
4
5
4
5
6
3
1
x
x
x
x
x
6
3
4
5
2
При этом
xn 1 , 1 xn 1.
1
1
1
Если , N 3; n 3 xn 1 ,
2
2
2
1
1
1
а для , N 6; n 6 xn 1 .
5
5
5
48. пример 3
49. Кому нужен такой «формализм»?
50.
ОтветПоследовательность
1
n
не имеет предела, так как
нельзя указать номер, после которого все члены
последовательности окажутся в сколь угодно малой
окрестности какого-либо числа.
Последовательности, не имеющие предела, называются
расходящимися.
51. 4-3 Основные теоремы о пределах
• Единственность предела• Предел суммы, произведения, частного
• Признаки существования предела
52. Единственность предела
53. Предел суммы
54. Пределы произведения и частного
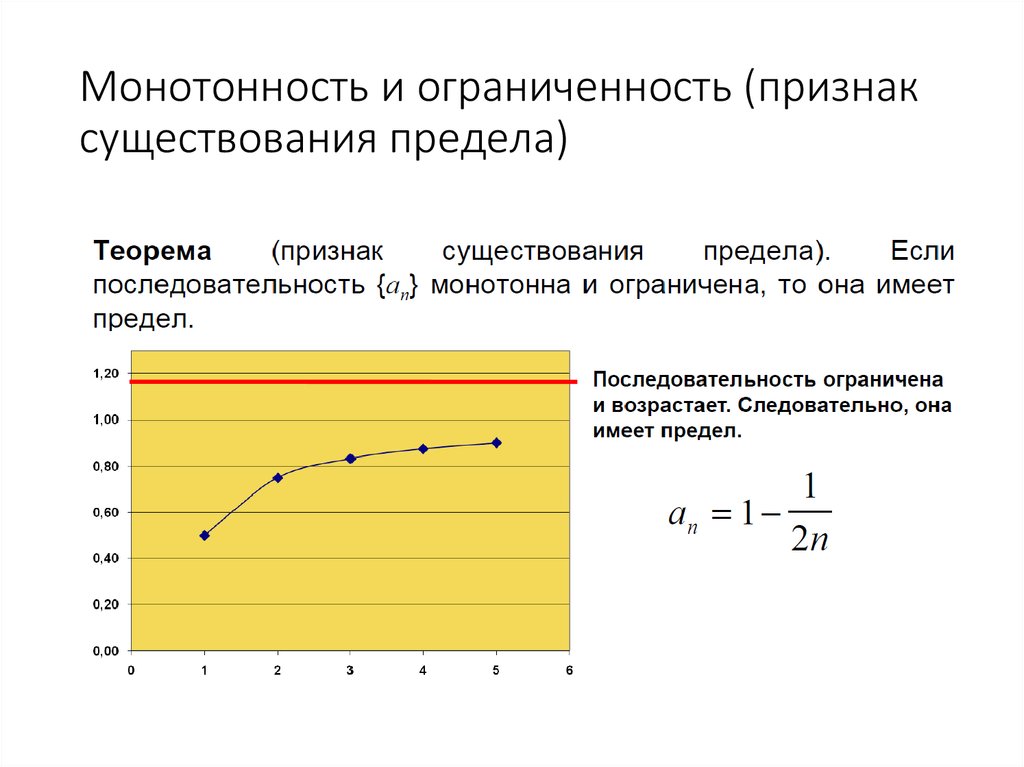
55. Монотонность и ограниченность (признак существования предела)
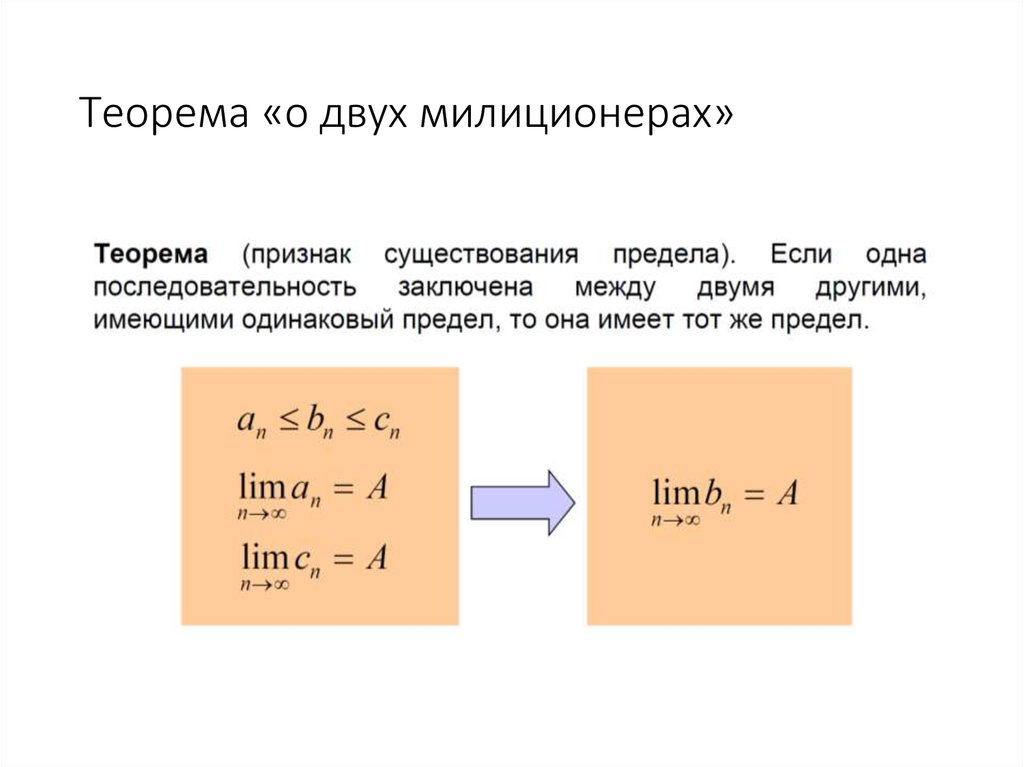
56. Теорема «о двух милиционерах»
57.
4-4 Бесконечно большие ибесконечно малые
последовательности
Последовательность x называется бесконечно
большой, если для любого положительного числа M
можно указать такое натуральное число N (зависящее
от M ), что при всех n N выполняется неравенство
n
xn M .
M 0 N N M : n N M xn M .
lim xn xn
n
n
58.
Последовательность xn называется бесконечномалой, если для любого сколь угодно малого
положительного
числа
найдется
такое
натуральное число N (зависящее от ), что при всех
n N выполняется неравенство xn .
lim xn 0 :
n
0 N : n N : xn .
59.
Свойства бесконечно малых последовательностей1. Бесконечно малая последовательность ограничена.
2. Сумма и разность двух бесконечно малых
последовательностей дает бесконечно малую
последовательность.
3. Произведение ограниченной последовательности
на бесконечно малую есть бесконечно малая
последовательность.
60.
Свойства бесконечно малыхпоследовательностей
4.
Произведение
двух
бесконечно
малых
последовательностей
есть
последовательность
бесконечно малая.
5.
Если
элементы
бесконечно
малой
последовательности xn не равны нулю, то
последовательность
1
xn
будет бесконечно большой.
6. Если xn бесконечно большая последовательность
и
xn 0 ,
малая.
то последовательность
1
xn
– бесконечно
61.
Примеры бесконечно малых последовательностей:1. Последовательность
sin n
n
– бесконечно малая,
т.к. ее элементы являются произведением элементов
sin n и
ограниченной
последовательности
бесконечно малой последовательности
1
.
n
62.
Примеры бесконечно малыхпоследовательностей
2. Последовательность
n 1
3
n
– бесконечно малая, т.к.
является
суммой
бесконечно
последовательностей n1 и n1 .
2
3
малых
63. 4-5 Вычисление пределов
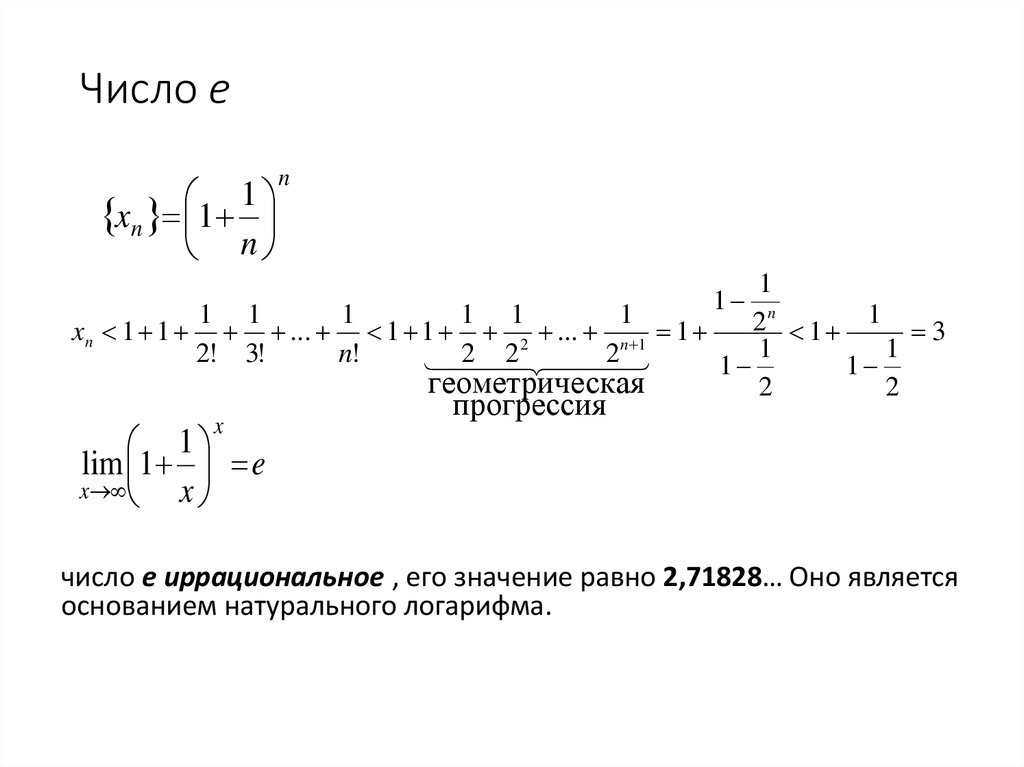
64. Число е
1xn 1
n
n
1
1 1
1
1 1
1
2n 1 1 3
xn 1 1 ... 1 1 2 ... n 1 1
1
1
2! 3!
n!
2
2
2
1
1
геометрическая
2
2
1
x
1
lim 1 e
x
x
прогрессия
число е иррациональное , его значение равно 2,71828… Оно является
основанием натурального логарифма.























































 mathematics
mathematics








