Similar presentations:
Введение в математический анализ
1. Введение в математический анализ
2. Функция. Способы задания функции.
3.
Определение: Величина y называется функциейпеременной величины x, если каждому числовому
значению x, принадлежащему некоторой области его
изменения
X,
соответствует
единственное
определенное числовое значение величины y Y .
Говорят, что на множестве задана функция
y f ( x)
х – независимая переменная (аргумент);
Х – область определения функции;
y – зависимая переменная;
Y – множество значений функции.
4.
Определение: Графиком функции y f xназывается множество точек плоскости хОу
координатами x; f ( x) .
с
Определение: Функция y f ( x ) называется четной,
если для любого x X выполняется равенство
f x f x и
нечетной,
если
выполняется
равенство f x f x .
График четной функции симметричен относительно
оси ординат (Оу), а график нечетной функции
симметричен относительно начала координат О(0; 0).
5.
Определение:Функция y f ( x )
называется
периодической, если существует такое числоT 0 , что
для любых x X выполняется равенство:
f x T f x .
y f ( x ) называется
Определение: Функция
ограниченной на промежутке Х, если существует
такое число M 0 , что f x M для любого x X .
6.
Определение: Если уравнение y f x может бытьоднозначно разрешено относительно переменной х, то
существует функция x g ( y ) , которая называется
обратной по отношению к функции y f x . При
этом y f g ( y ) .
Определение: Если функция задана в виде
y f u
где u x , то функция y f x называется
сложной функцией (функцией от функции). Функция
u x называется промежуточным аргументом.
7.
Определение: Функция, заданная уравнениемF ( x; y ) 0 , неразрешённым относительно зависимой
переменной у, называется неявной функцией.
Термины «явная функция» и «неявная функция
характеризуют способ задания функции.
Каждая явная функция может быть представлена в
неявном виде: y f ( x) 0.
Но не каждая неявно заданная функция может быть
6
2
y
y
x
0
представлена явно. Например,
не
выражается через элементарные функции, то есть это
уравнение невозможно разрешить относительно у.
8.
Определение: Если значения переменных х и узависят от параметра t, значения которого изменяются
в интервале T1; T2 , то говорят, что функция задана
параметрически:
x (t );
y (t ).
Каждому значению t соответствуют значения х и у.
Если х и у рассматривать как координаты точек на
координатной плоскости Оху, то каждому значению t
будет соответствовать определенная точка плоскости.
Когда t изменяется от Т1 до Т2, эти точки на
плоскости описывают некоторую кривую.
9.
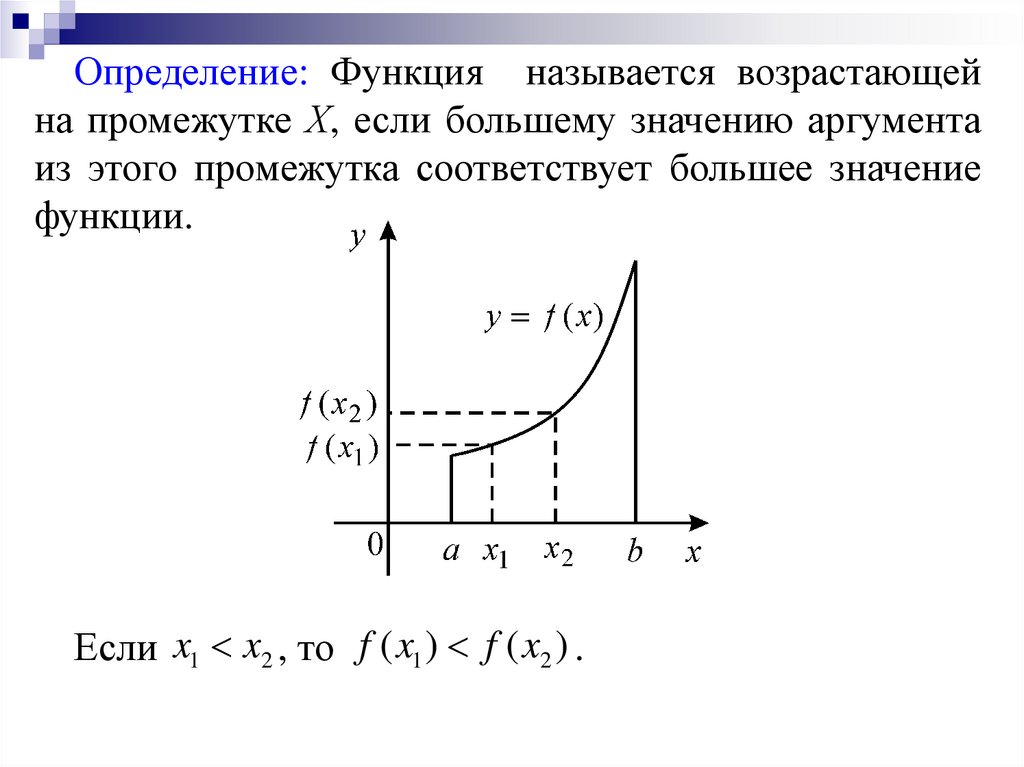
Определение: Функция называется возрастающейна промежутке Х, если большему значению аргумента
из этого промежутка соответствует большее значение
функции.
Если x1 x2 , то f ( x1 ) f ( x2 ) .
10.
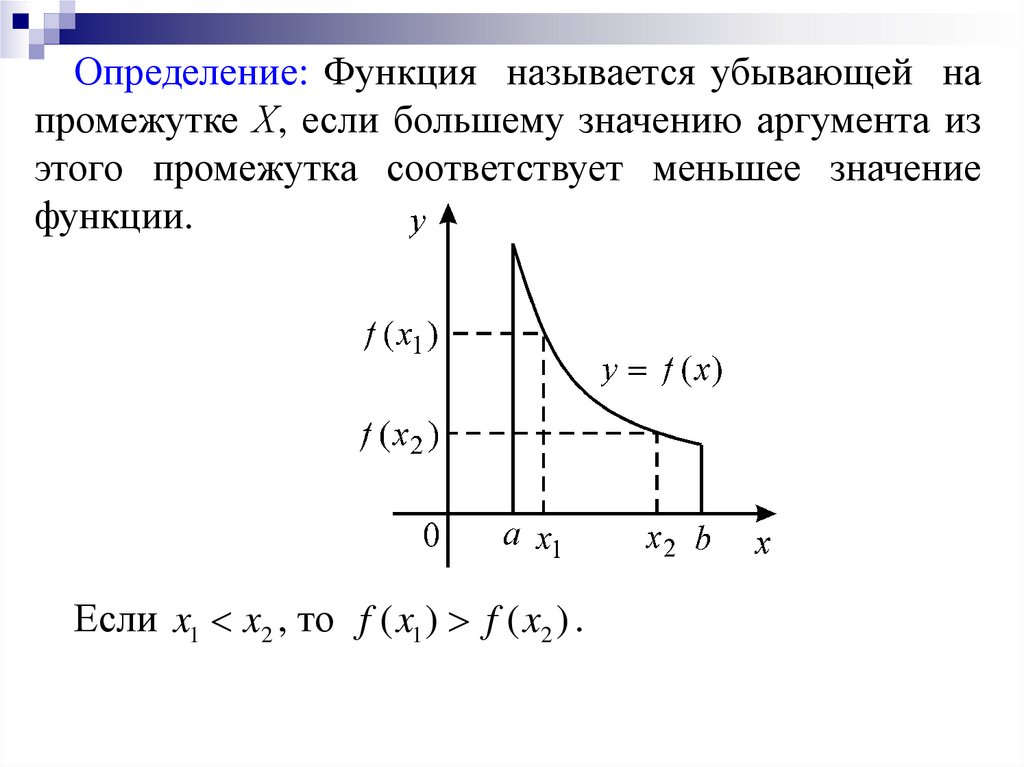
Определение: Функция называется убывающей напромежутке Х, если большему значению аргумента из
этого промежутка соответствует меньшее значение
функции.
Если x1 x2 , то f ( x1 ) f ( x2 ) .
11.
Можноввести
понятия
неубывающей
(невозрастающей) функции.
Определение: Функция называется монотонной на
промежутке
Х,
если
она
является
либо
невозрастающей, либо неубывающей на Х.
12. Предел функции
13.
Определение: Функция y f ( x ) стремится к пределуb при х стремящимся к a, если для любого 0 , как
бы мало оно не было, можно указать такое число 0
( ), что для всех значений х, отличных от а, и
удовлетворяющего условию x a , выполняется
неравенство f x b .
f x b .
Обозначают предел функции: lim
x a
Математически определение предела функции
записывают в виде:
0 ( ) 0, что при x a f ( x) b
14.
Геометрически число b есть предел функции f xпри x a , если для любого 0 найдется такая
-окрестность точки а, что для всех x a из этой
-окрестности соответствующие точки графика
функции y f x лежат внутри полосы шириной 2 ,
ограниченной прямыми y b и y b .
15. Односторонние пределы
f x стремится к пределу b1Если
при х
стремящимся к а так, что х принимает только
значения из интервала a ; a , то b1 называют
пределом функции f x в точке а слева, и пишут:
lim f x b1 .
x a 0
16.
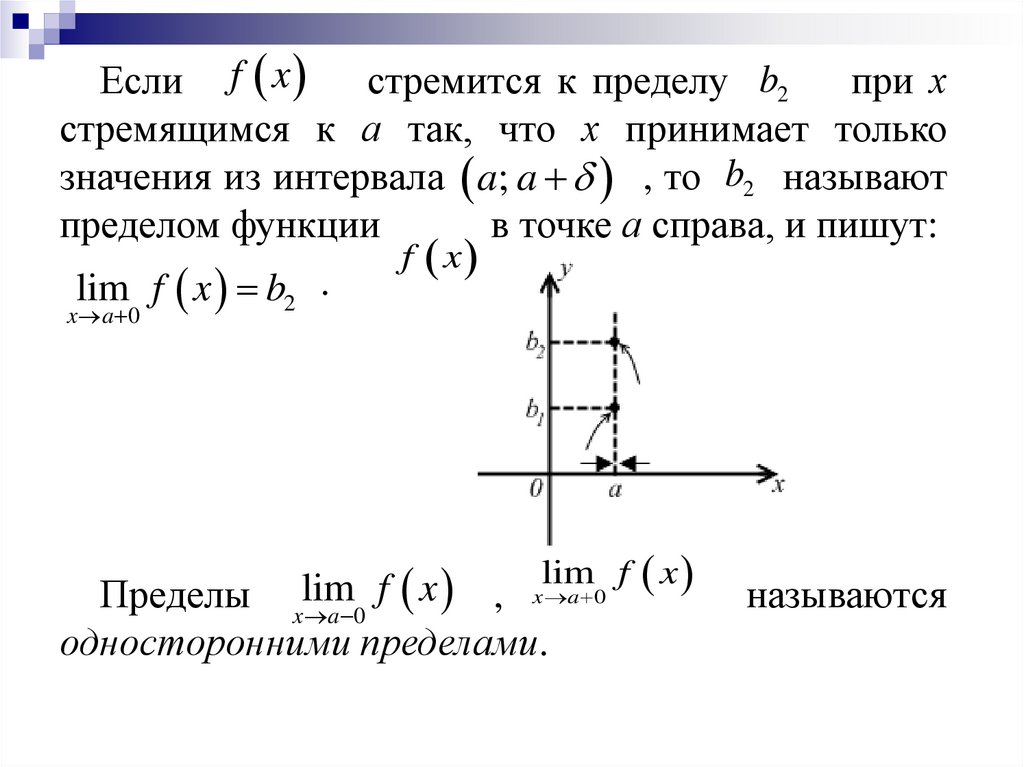
Если f xстремится к пределу b2
при х
стремящимся к а так, что х принимает только
значения из интервала a; a , то b2 называют
пределом функции
в точке а справа, и пишут:
f x
lim f x b2 .
x a 0
lim f x
lim
f
x
Пределы x a 0
, x a 0
односторонними пределами.
называются
17.
Пример: Рассмотрим функцию знака:1, при х 0;
y sign x 0, при х 0;
1, при х 0.
Функция в точке х=0 имеет
левый и правый пределы:
lim sign x 1
x 0
lim sign x 1
x 0
18.
Теорема: Функция f x имеет предел в точке x aтогда и только тогда, когда в этой точке существуют
как левый, так и правый конечные пределы и они
равны между собой, то есть
lim f x lim f x lim f x b.
x a 0
x a 0
x a
Замечание: Для существования предела функции
при х стремящимся к а не требуется, чтобы функция
была определена в точке x a . Необходимо, чтобы
функция была определена в окрестности точки а.
19.
x2 44 .
Пример: Доказать, что lim
x 2 x 2
Решение:
2
x 4
Функция x 2 не определена при х=2. Докажем,
что при произвольном ε найдется δ, что будет
выполняться неравенство:
x2 4
4 , если x 2
x 2
При x 2 неравенство эквивалентно неравенству:
x2 4
( x 2)( x 2)
4
4 x 2 4 x 2
x 2
x 2
x2 4
Поэтому δ= ε и, следовательно, lim
4.
x 2 x 2
20.
Определение: Функция f(x) стремится кбесконечности при х стремящимся к а, если для
каждого M 0 , как бы велико оно не было, можно
указать такое число 0 , что для всех значений х,
удовлетворяющих условию x a , имеет место
неравенство f x M .
Обозначается lim f x .
x a
В этом случае функция f(x)
бесконечно большой (б. б.) при х→а.
называется
21.
Бесконечно малые функцииОпределение: Функция x
называется
бесконечно малой (б. м.) при x a , если lim x 0.
x a
Из определения следует, что для любого 0 ,
можно указать такое число 0 , что для всех
значений х, отличных от а, и удовлетворяющего
условию x a , выполняется неравенство x .
Между бесконечно малыми и бесконечно
большими величинами существует связь:
C
C
á. á.,
á. ì ., где С – постоянное число.
á. ì .
á. á.
22.
Основные теоремы о пределах1. Предел суммы двух функций равен сумме
пределов от каждой функции:
lim f1 x f 2 x lim f1 x lim f 2 x .
x a
x a
x a
2. Постоянное число можно выносить за знак
предела:
lim C f x C lim f x .
x a
x a
23.
3. Предел произведения двух функций равенпроизведению пределов от каждой функции:
lim f1 x f 2 x lim f1 x lim f 2 x .
x a
x a
x a
n
Следствие: lim f x lim f x .
n
x a
x a
4. Предел частного двух функций равен частному
пределов от каждой функции:
f1 x
f1 x lim
lim
x a
, lim f 2 x 0 .
x a f x
x a
lim f 2 x
2
x a
24.
Если не возникает никаких неопределенностей, топредел функции вычисляется непосредственной
подстановкой вместо х предельного значения.
Например:
5 x 1 5( 1) 1 6
lim 2
3;
2
x 1 x 1
( 1) 1 2
x2 9
9 9
0
lim
0;
x 3 2 x 1
2 3 1 7
3x 1 3 2 1
5
lim 2
б.б. .
x 2 x 4
4 4
б. м.
25. Неопределенности. Способы разрешения неопределенностей.
26. Разрешение неопределенностей
Существует несколько видов неопределенностей:0
0
1
0
0
0
1. Неопределенность вида .
0
При возникновении такой неопределенности
возможны два случая:
а) выражение, стоящее под знаком предела,
представляет собой дробно-рациональную функцию;
б) выражение, стоящее под знаком предела,
содержит дробно-иррациональную функцию.
27.
а) выражение, стоящее под знаком предела,представляет собой дробно-рациональную функцию
Если числитель и знаменатель такой функции
обращаются в 0, это означает, что число, к которому
стремится аргумент является корнем многочленов
числителя и знаменателя.
Поэтому числитель и знаменатель необходимо
разложить на множители и сократить на общий
множитель.
Многочлены
второй
степени
раскладывают на множители по корням х1 и х2:
ax bx c a x x1 x x2 .
2
28.
x2 4 x 5Пример. Вычислить предел: lim 2
.
x 1 x 3 x 2
Решение:
Разложим числитель и знаменатель на множители,
для этого определим корни многочленов:
b D
2
D b 4ac, x1,2
.
2a
x 2 4 x 5 0, D 36, x1 1, x2 5.
x 2 3x 2 0, D 1, x1 1, x2 2.
x 1 x 5
x2 4x 5 0
x 5 6
lim 2
lim
lim
6
x 1 x 3 x 2
x
1
x
1
x 1 x 2
x 2 1
0
29.
3x 2 2 x 5Пример. Вычислить предел: lim 2
x 1 2 x 7 x 5
Решение:
При разложении числителя и знаменателя на
множители можно производить деление многочлена
на многочлен в столбик:
3x 2 x 5 x 1
2
3x 5
3x 3x
2 x2 7 x 5 x 1
2
2x 5
2x 2x
5x 5
5x 5
5x 5
5x 5
2
0
0
3x 2 2 x 5 0
x 1 3x 5 lim 3x 5 8 8
lim 2
lim
x 1 2 x 7 x 5
3
0 x 1 x 1 2 x 5 x 1 2 x 5 3
30.
б) выражение, стоящее под знаком предела,содержит дробно-иррациональную функцию
В этом случае для раскрытия неопределенности и
числитель и знаменатель дроби умножают на
сопряженное выражение к иррациональному
выражению, используя формулу разности квадратов:
a b a b a b
2
2
31.
Пример. Вычислить предел: limx 3
x 3
5x 1 4
Решение:
Здесь знаменатель дроби является иррациональным
выражением, поэтому домножим и числитель и
знаменатель дроби на выражение сопряженное к
знаменателю:
lim
x 3
x 3
( x 3)( 5 x 1 4)
0
lim
x 3 ( 5 x 1 4)( 5 x 1 4)
5x 1 4 0
( x 3)( 5 x 1 4)
( x 3)( 5 x 1 4)
lim
lim
x 3
x
3
5 x 1 16
5 x 15
5x 1 4 8
( x 3)( 5 x 1 4)
lim
lim
x 3
x 3
5
5
5( x 3)
32.
3 1 4xПример. Вычислить предел: xlim
2
x 2
Решение:
Здесь числитель дроби является иррациональным
выражением, поэтому домножим и числитель и
знаменатель дроби на выражение сопряженное к
числителю:
(3 1 4 x )(3 1 4 x )
3 1 4x 0
lim
lim
x
2
x 2
x 2
( x 2)(3 1 4 x )
0
9 (1 4 x)
8 4x
lim
lim
x 2 ( x 2)(3 1 4 x )
x 2 ( x 2)(3 1 4 x )
4(2 x)
4
4 2
lim
lim
x 2 ( x 2)(3 1 4 x )
x 2 3 1 4 x
6 3
33.
Пример. Вычислить предел: lim 2 xx 4
3 2x 1
Решение:
Здесь и числитель и знаменатель дроби являются
иррациональными выражениями, поэтому домножим и
числитель и знаменатель дроби на выражения сопряженные и
к числителю и к знаменателю:
2 x
0 lim (2 x )(2 x )(3 2 x 1)
lim
x 4
x 4 3
(3 2 x 1)(3 2 x 1)(2 x )
2x 1 0
(4 x)(3 2 x 1) lim (4 x)(3 2 x 1)
lim
x 4
(8 2 x)(2 x )
x 4 (9 (2 x 1))(2
x)
(4 x)(3 2 x 1)
3 2x 1 6 3
lim
lim
x 4
x
4
2(4 x)(2 x )
2(2 x ) 8 4
34.
2. Неопределенность видаделить на бесконечность).
(бесконечность
В этом случае выражение, стоящее под знаком
предела, представляет собой частное многочленов.
Pn ( x)
.
Pm ( x)
Для разрешения такого вида неопределенности
необходимо разделить все слагаемые числителя и
знаменателя на переменную х в старшей степени и
рассмотреть
предел
каждого
слагаемого
в
отдельности.
35.
3 x 2 10 x 8Пример. Вычислить предел: lim
x x 2 5 x 4
Решение:
3 x 2 10 x 8
2 2
2
2
x
x
3x 10 x 8 lim x
lim 2
x x 2 5 x 4
x x 5 x 4
2 2
2
x
x
x
10 8
3 2
x x 3
lim
x
5 4
1 2
x
x
36.
2 x 2 3x 1Пример. Вычислить предел: lim
x
5x 1
Решение:
2 x 2 3x 1
2 2
2
2 x 2 3x 1
x
x
lim
lim x
x
5x 1
x 5 x 1
x2 x2
3 1
2 2
2
x
x
lim
x
5 1
б
.
м
.
2
x x
37.
3x 2 5Пример. Вычислить предел: lim 3
x x x 4
Решение:
3x 2 5
3
3
x
3x 2 5
lim 3 x
lim 3
x x
x
4
x x x 4
3 3
3
x
x
x
б. м.
lim
0
x
1 4
1 2 3
x
x
38.
3. Неопределенность вида .Для разрешения неопределенности такого вида,
необходимо умножить и разделить на выражение
сопряженное иррациональному выражению.
39.
х 4 x 2 3x )Пример. Вычислить /предел: lim(2
x
Решение:
lim(2 х 4 x 2 3 x )
x
lim
x
(2 х 4 x 3x )(2 х 4 x 3x )
2
2
(2 х 4 x 3x )
2
lim
x
4 x 2 (4 x 2 3 х)
2 х 4 x 2 3x
3 x
3 x
3
lim
lim
lim
x
4
2 х 4 x 2 3 x x 2 х 4 x 2 x 4 x
3x
40. I замечательный предел
Первыйзамечательный
предел
разрешает
неопределенность вида 0 и имеет вид:
0
sin x
x
lim
1
lim
1
x 0
x
0
x
sin x
Первый замечательный предел используют в тех
случаях, когда выражение, стоящее под знаком
предела содержит тригонометрические функции.
Частные случаи первого замечательного предела:
sin kx
kx
lim
1
lim
1
x 0
x
0
kx
sin kx
41.
Пример. Вычислить предел:tg x
lim
x 0 x
Решение:
sin x
sin x
1
lim
lim
1
tg x 0 lim
x 0 cos x
lim
x 0 x cos x x 0 x
x 0
x
0
42.
Пример. Вычислить предел: limsin 3x ctg 5 xx 0
Решение:
cos5 x
limsin 3 x ctg 5 x 0 limsin 3 x
x 0
x 0
sin 5 x
3 x sin 3 x cos5 x 5 x lim 3 x cos5 x 3
lim
x 0
5x
5
x 0
3 x sin 5 x 5 x
43.
Пример. Вычислить предел: lim 1 cos 6 xx 0 x sin x
Решение:
1 cos 6 x 0
2sin 2 3 x
lim
lim
x 0 x sin x
x
0
x sin x
0
2
18
x
2sin 3 x sin 3 x x 3 x 3 x lim
lim
x 0 2 18
x 0
x
3 x 3 x x sin x x
44.
arctg 4 xПример. Вычислить предел: lim
x 0
3x
Решение:
y arctg 4 x
4 x tgy
arctg 4 x 0
y
lim
lim
1
x 0
y 0
1
3x
0 x tgy
3 tgy
4
4
x 0 y 0
4
y cos y 4
4
lim
lim cos y
3 y 0 sin y
3 y 0
3
45. II замечательный предел
Второйзамечательный
предел
разрешает
неопределенность вида 1 и имеет вид:
x
1
lim 1 e
x
x
1
x
lim 1 x e
x 0
где e 2, 7
Показательная функция с основанием е имеет
вид:
y e x и называется экспонентой.
Логарифм с основанием е имеет вид: loge x ln x и
называется натуральным.
y
Если e x , то y ln x.
46.
1Пример. Вычислить предел: lim 1
x
x
3x
Решение:
3
1
1
lim 1 1 lim 1 e3
x
x
x х
3x
х
47.
3Пример. Вычислить предел: lim 1
x
2x 1
3 x
Решение:
3 x
3 х
3
1 lim 1
x
2 х 1 3
2 x 1 2 х 1 (3 х )
3 х
3
1
1
lim 1
lim 1
x
x
2x 1
2
х
1
3
3
3
lim 1
x
2x 1
e
9 3 x
x 2 x 1
lim
e
3x
x 2 x
lim
e
3
2
48.
2x 3Пример. Вычислить предел: lim
x 2 x 5
2 x 1
Решение:
2x 3
lim
x 2 x 5
2 x 1
(2 x 5) 5 3
lim
1 x
2x 5
2 x 1
2 x 5
8
2 x 1
1
8
2x 5
lim
1
lim
2x 5
x
x
2x 5 2x 5
8
16 x 8
16 x
e
lim
x
2 x 5
e
lim
x
2x
e
8
8
(2 x 1)
2 x 5
49.
Пример. Вычислить предел: lim(5 2 x)3x
2 x
x 2
.
Решение:
lim(5 2 x)
x 2
3x
2 x
y x 2
1 x y 2
x 2 y 0
lim(5 2( y 2))
3( y 2)
2 ( y 2)
y 0
1
2 y
lim (1 ( 2 y ))
y 0
lim(5 2 y 4)
y 0
2 y 3 y 6
1 y
e
lim (6 y 12)
y 0
3 y 6
y
e12 .
50.
Пример. Вычислить предел:lim(2 x 3) ln( x 2) ln x
x
Решение:
Преобразуем выражение стоящее под знаком
предела, используя свойства логарифмической
функции:
b
log a b n n log a b
log a b log a c log a
c
x 2
lim(2 x 3) ln( x 2) ln x lim(2 x 3) ln
x
x
x
51.
Сначала разрешим неопределенность, а затемвычислим логарифм полученного числа.
x 2
lim ln
x
x
2 x 3
x 2
ln lim
x
x
2 x 3
x
2
2 x 3
1
2
ln lim 1
ln lim 1
x
x
x
x
2
ln e
4 x 6
x x
lim
ln e 4 4.
2
(2 x 3)
x
52.
2x 3Пример. Вычислить предел: lim
x 4 x 3
Решение:
2x 3
lim
x 4 x 3
3 x 1
2x
lim
x 4 x
3 x 1
1
lim
x 2
3 x 1
3 x 1
В дальнейшем решении возможны два случая:
1
lim
x 2
3 x 1
1
lim
x 2
3 x 1
1
lim
x 2
б .б .
1
lim
x 2
2 б .б . б.б.
б .б .
1
1
б .б .
0
2
б.б.
53. Непрерывность функции
54.
Пусть функция y f ( x) определена при некоторомзначении x0 и в некоторой окрестности с центром в
точке x0 . Пусть y0 f ( x0 ).
Аргументу х придадим некоторое приращение x .
x0
y0 f ( x0 )
x0 x
y0 y f ( x0 x)
Тогда приращение функции выразится формулой:
y f x0 x f ( x0 )
55.
y f ( x)Определение: Функция
называется
непрерывной в точке x0 , если она определена в точке
x0 и некоторой ее окрестности, и если
lim y 0 или lim ( f ( x0 x) f ( x0 )) 0
x 0
x 0
Условие непрерывности записывают в виде:
lim f x0 x f ( x0 ).
x 0
Геометрически непрерывность функции в точке
означает, что разность ординат графика функции
y f ( x) в точках x0 x и x0 будет по абсолютной
величине малой, если только x будет достаточно
малой.
56.
Условия непрерывности:1. Функция должна быть определена в точке х=х0,
то есть существует f(x0).
2. В этой точке должны существовать конечные
односторонние пределы lim f ( x) è lim f ( x).
x x0 0
x x0 0
3. Эти пределы должны быть равны между собой:
lim f ( x) lim f ( x).
x x0 0
x x0 0
4. Эти пределы должны быть равны значению
функции в этой точке:
lim f ( x) lim f ( x) f ( x0 ).
x x0 0
x x0 0
57.
Если в какой-либо точке х=х0 для функции невыполняется по крайней мере одно из условий
непрерывности, то в точке х=х0 функция имеет
разрыв, а точка х=х0 называется точкой разрыва
функции y=f(x).
58.
Классификация точек разрыва:Устранимый разрыв
Определение: Точка х=х0 называется точкой
устранимого разрыва функции y=f(x), если в данной
точке существуют конечные односторонние пределы
и они равны между собой, но функция в данной
точке неопределена.
59.
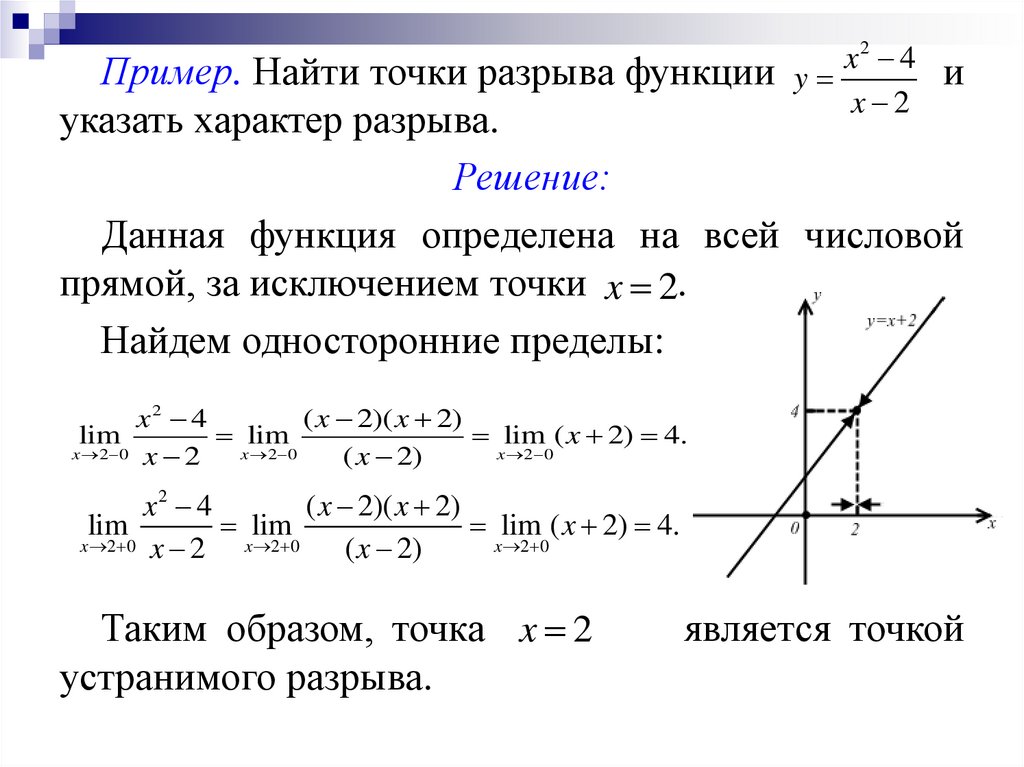
x2 4Пример. Найти точки разрыва функции y
x 2
и
указать характер разрыва.
Решение:
Данная функция определена на всей числовой
прямой, за исключением точки x 2.
Найдем односторонние пределы:
x2 4
( x 2)( x 2)
lim
lim
lim ( x 2) 4.
x 2 0 x 2
x 2 0
x 2 0
( x 2)
x2 4
( x 2)( x 2)
lim
lim
lim ( x 2) 4.
x 2 0 x 2
x 2 0
x 2 0
( x 2)
Таким образом, точка x 2
устранимого разрыва.
является точкой
60.
Разрыв первого родаОпределение: Точка x x0
называется точкой
разрыва I рода для функции y f ( x) , если в данной
точке существуют конечные односторонние пределы,
но они не равны между собой.
61.
2xПример. Найти точки разрыва функции y
x
и
указать характер разрыва.
Решение:
Данная функция определена на всей числовой
прямой, за исключением точки x 0.
Найдем односторонние пределы.
2x
2x
2x
2x
lim
lim
2, lim
lim
2,
x 0 x
x 0 x
x 0 x
x 0 x
Так как
x, если x 0
x
x, если x 0
Таким образом, точка x 0является точкой разрыва
I рода.
62.
Разрыв второго родаОпределение: Точка x x0
называется точкой
разрыва II рода для функции y f ( x) , если в данной
точке хотя бы один из односторонних пределов
обращается в бесконечность.
63.
1x
Пример. Найти точки разрыва функции y 2 и
указать характер разрыва.
Решение:
Точка x 0 является точкой разрыва II рода, так
как находя односторонние пределы, получим:
1
x
lim 2 lim 2
x 0
x 0
1
x
lim 2 lim 2
x 0
1
б . м.
x 0
1
б . м.
2
б .б .
1
1
б .б .
б. м. 0
2
б.б.
2 б .б . б.б.



























































 mathematics
mathematics








