Similar presentations:
В математике есть нечто, вызывающее восторг
1.
Девиз нашего урока:«В математике есть
нечто,
вызывающее восторг».
2.
Повторение основных понятийТест
1. Медиана – это …
2. Высота – это …
3. Биссектриса – это …
3.
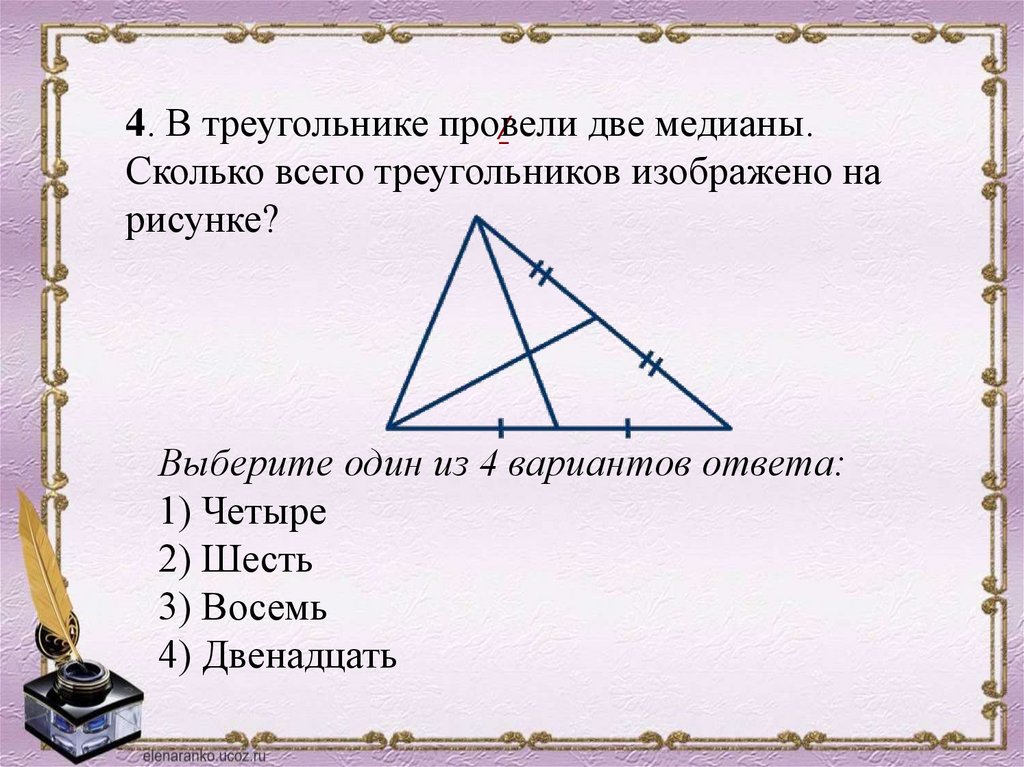
4. В треугольнике провелидве медианы.
/
Сколько всего треугольников изображено на
рисунке?
Выберите один из 4 вариантов ответа:
1) Четыре
2) Шесть
3) Восемь
4) Двенадцать
4.
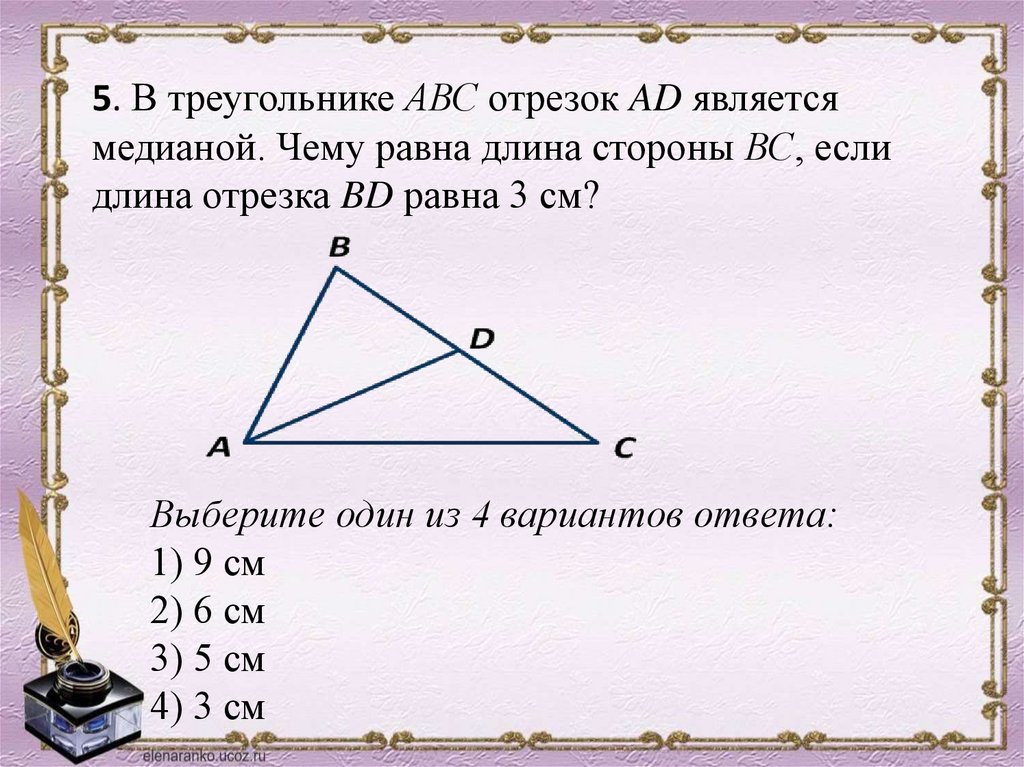
5. В треугольнике АВС отрезок AD являетсямедианой. Чему равна длина стороны ВС, если
длина отрезка BD равна 3 см?
Выберите один из 4 вариантов ответа:
1) 9 см
2) 6 см
3) 5 см
4) 3 см
5.
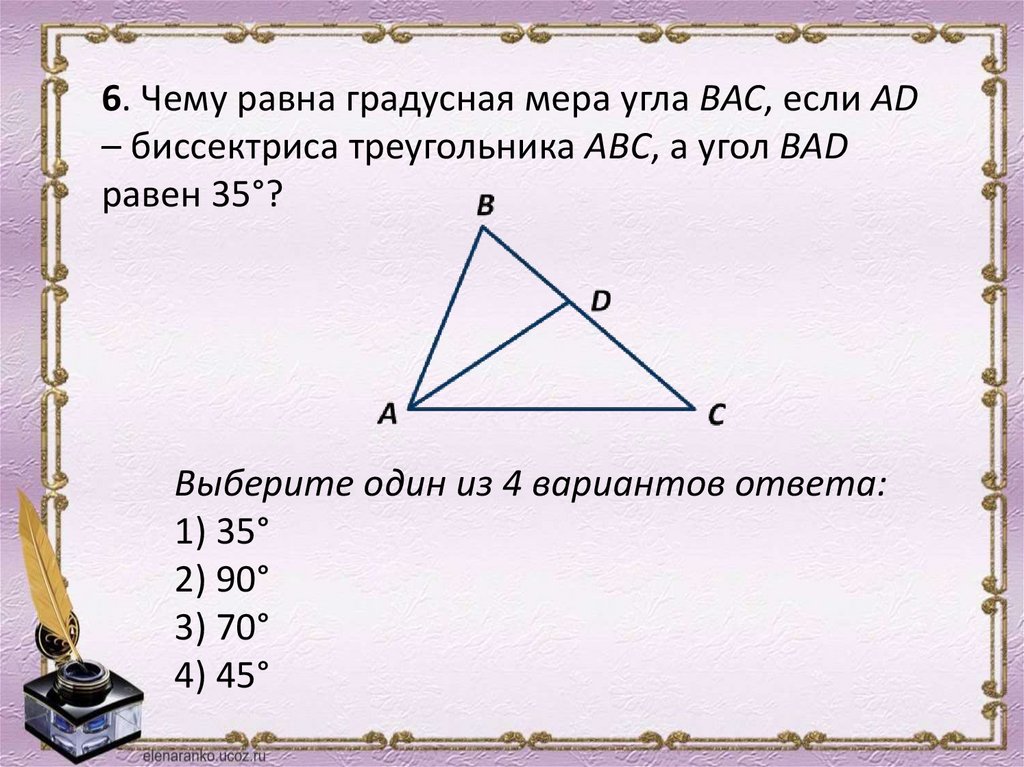
6. Чему равна градусная мера угла ВАС, если АD– биссектриса треугольника АВС, а угол ВАD
равен 35°?
Выберите один из 4 вариантов ответа:
1) 35°
2) 90°
3) 70°
4) 45°
6.
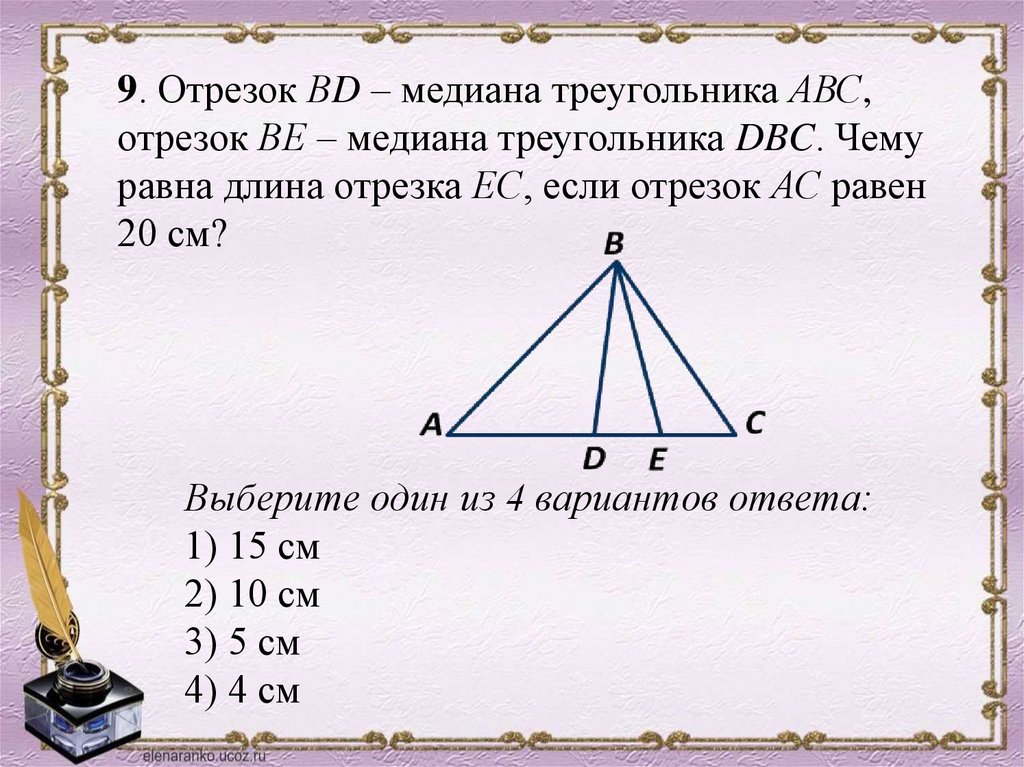
9. Отрезок ВD – медиана треугольника АВС,отрезок ВЕ – медиана треугольника DBC. Чему
равна длина отрезка ЕС, если отрезок АС равен
20 см?
Выберите один из 4 вариантов ответа:
1) 15 см
2) 10 см
3) 5 см
4) 4 см
7.
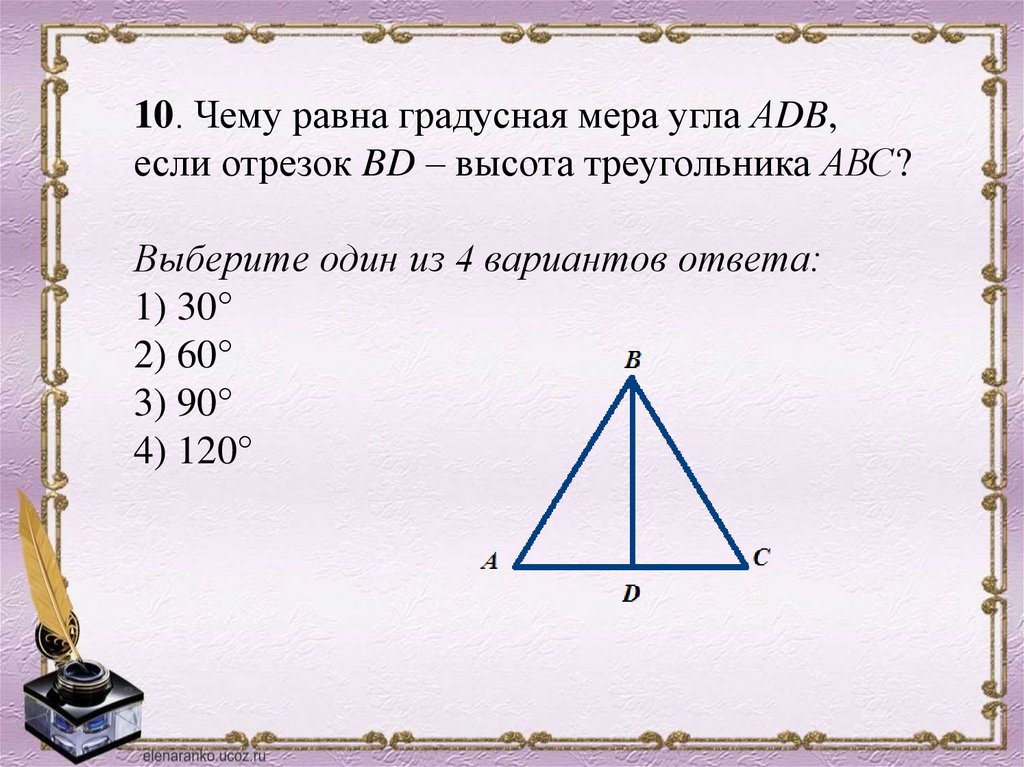
10. Чему равна градусная мера угла АDB,если отрезок BD – высота треугольника АВС?
Выберите один из 4 вариантов ответа:
1) 30°
2) 60°
3) 90°
4) 120°
8.
Какие виды треугольников вамзнакомы?
9.
Треугольники по видам углов.тупоугольный
остроугольный
прямоугольный
10.
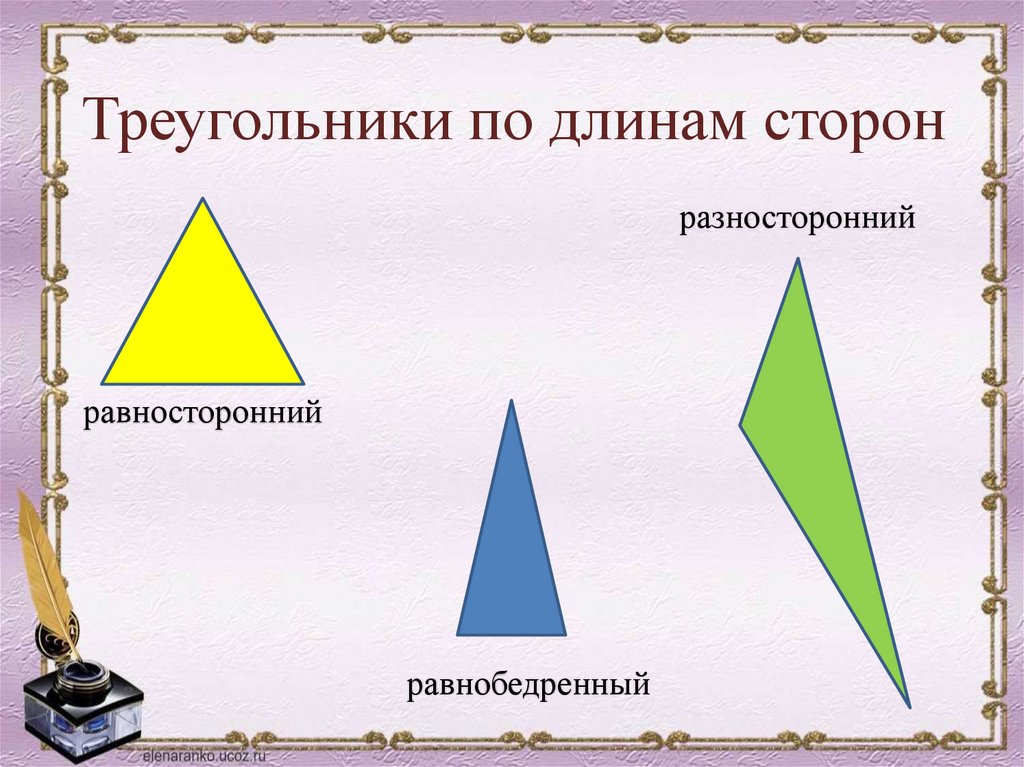
Треугольники по длинам сторонразносторонний
равносторонний
равнобедренный
11.
В треугольнике моёмДве стороны есть равных
И живут они вдвоём
При основании славном!
12.
Свойстваравнобедренного
треугольника
7 класс
13.
Определение.• Треугольник две
стороны которого
равны, называется
равнобедренным.
14.
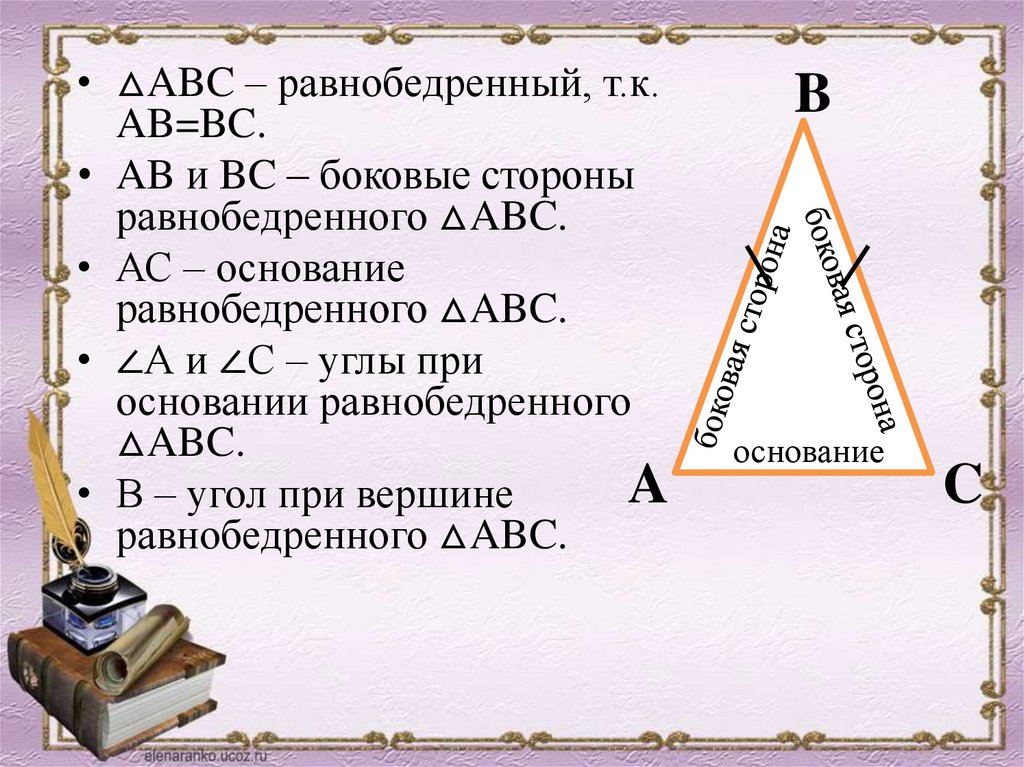
• △ABC – равнобедренный, т.к.AB=BC.
• AB и BC – боковые стороны
равнобедренного △ABC.
• АС – основание
равнобедренного △ABC.
• ∠А и ∠С – углы при
основании равнобедренного
△ABC.
A
• В – угол при вершине
равнобедренного △ABC.
B
основание
C
15.
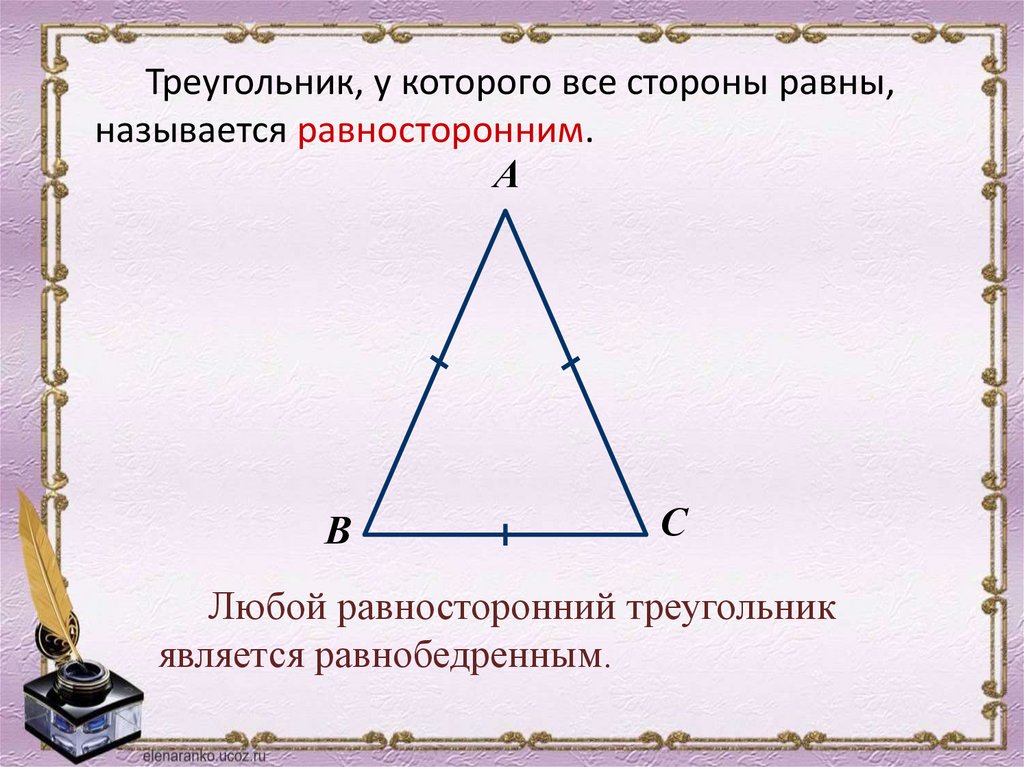
Треугольник, у которого все стороны равны,называется равносторонним.
А
В
С
Любой равносторонний треугольник
является равнобедренным.
16.
ТЕОРЕМА. В равнобедренном треугольникеуглы при основании равны.
C
A
Дано:
△ABC – равнобедренный, АC=AB.
Доказать: ∠B= ∠C.
Доказательство:
Рассмотрим равнобедренный △ABC:
Пусть AD – биссектриса △ABC.
D
B
△ABD= △ACD по первому при признаку
равенства треугольников (АВ=ВС по условию,
AD – общая сторона, ∠1= ∠2, т.к. AD –
биссектриса). В равных треугольниках против
равных сторон лежат равный углы, => ∠B= ∠C.
17.
2. В равнобедренномтреугольнике биссектриса,
проведённая к основанию,
является медианой и высотой.
18.
Дано: △ABC – равнобедренный,АВ=AС, AD - биссектриса.
Доказать: AD – медиана и высота.
A
C
D
B
Доказательство:
△ABD= △ACD, => BD=DC и ∠3=∠4.
т.к. BD=DC, то D – середина BC =>
AD – медиана.
т.к. ∠3 и ∠4 – смежные и равный друг
другу, то они прямые => AD – высота.
19.
2. В равнобедренномтреугольнике биссектриса,
проведённая к основанию,
является медианой и высотой.
• Высота равнобедренного
треугольника, проведённая к основанию,
является медианой и биссектрисой.
• Медиана равнобедренного
треугольника, проведённая к основанию,
является высотой и биссектрисой.
20.
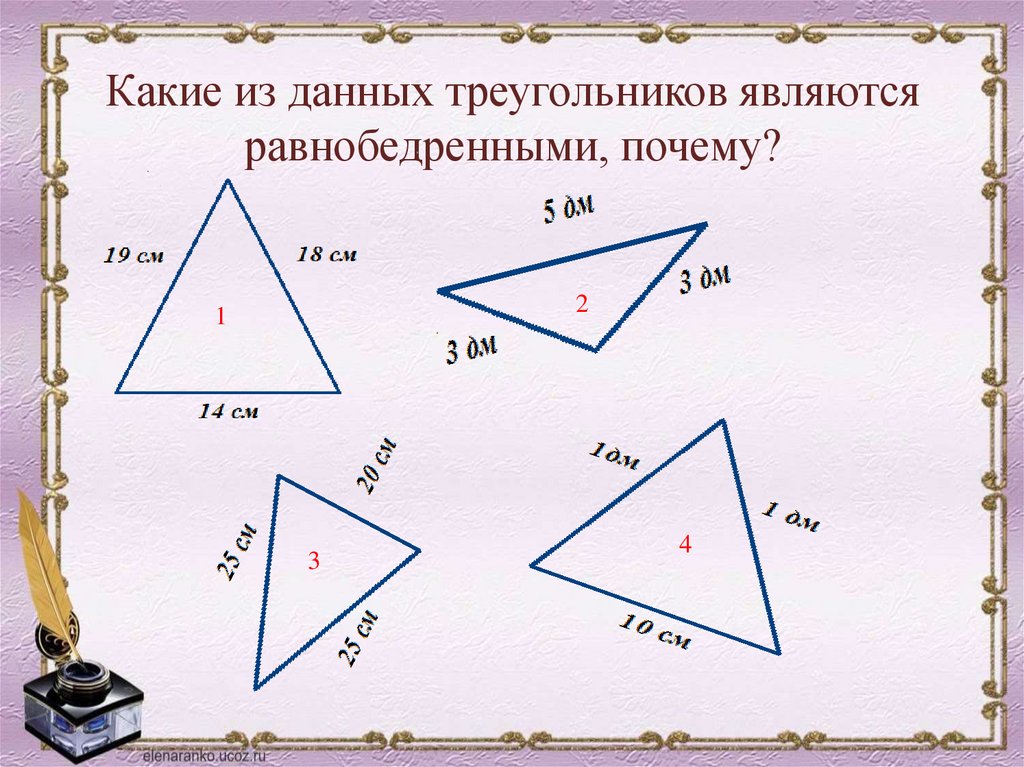
Какие из данных треугольников являютсяравнобедренными, почему?
2
1
3
4
21.
Домашнее задание:• П. 18 (с.48 ?10-13),
• № 108, 110, 112.
22.
23.
24.
25.
ACAC
BC
равны
равносторонний
AC
BC
AC
равносторонний
26.
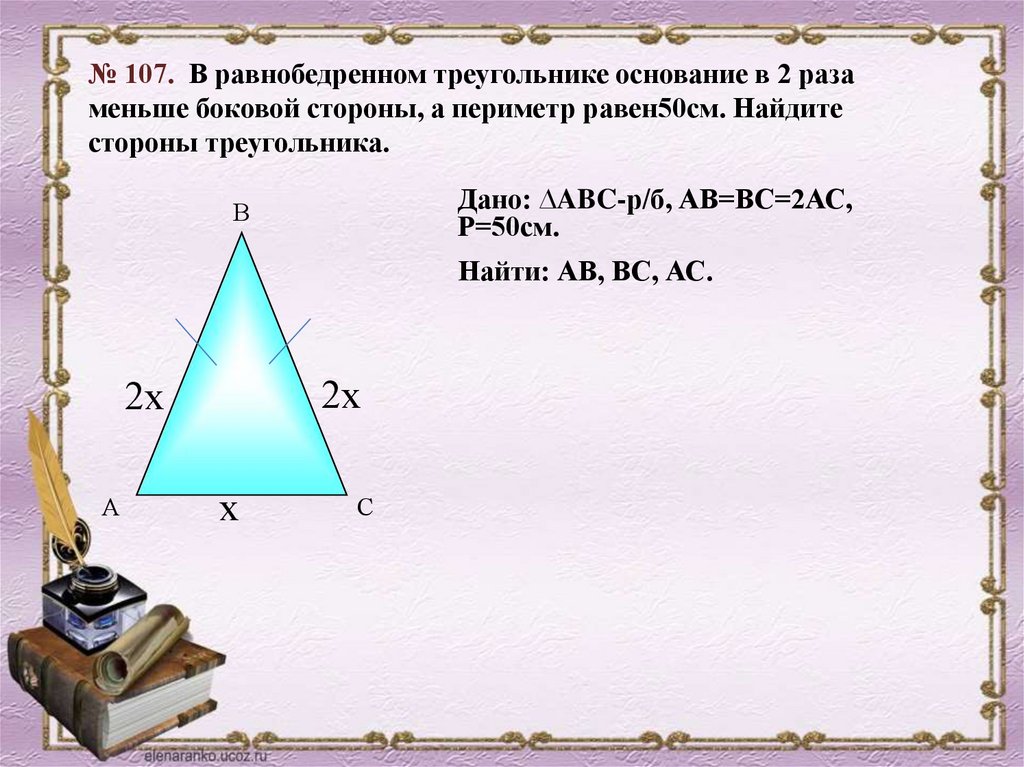
Классная работа 15.11.19• № 107
• № 111
• № 114
• № 115
• № 120
27.
№ 107Дано:
△ABC – равнобедренный, AC –
основание, AC < AB и BC в 2р.
PABC=50 см.
Найти:
AB, BC, AC.
Решение:
28.
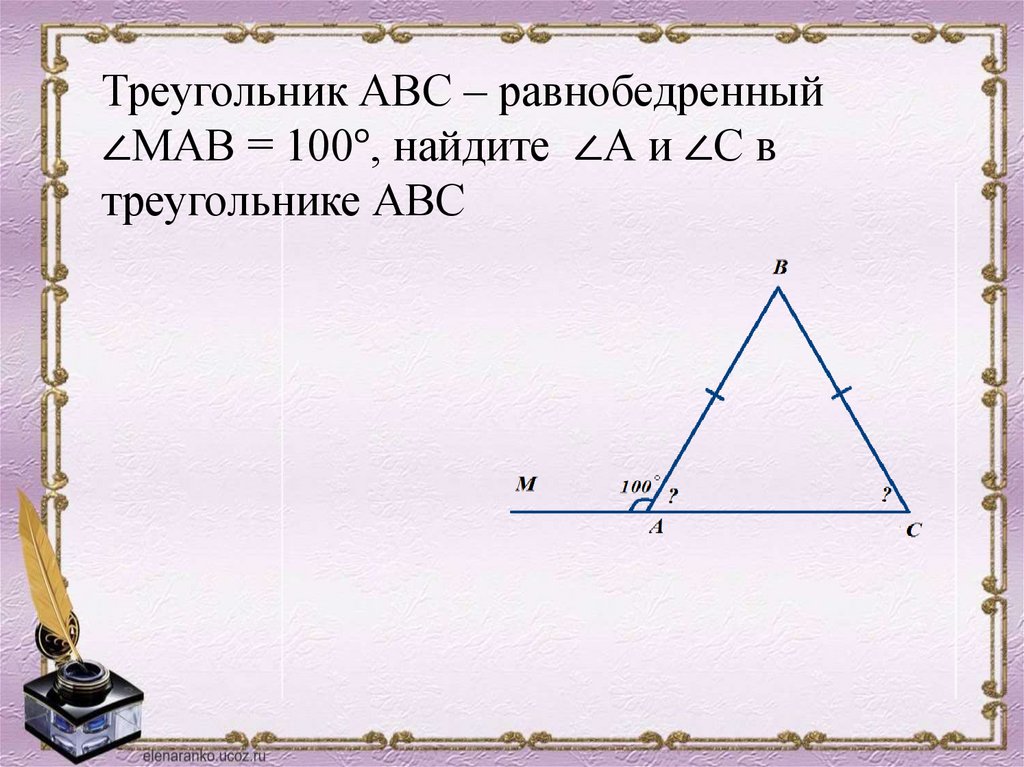
Треугольник АВС – равнобедренный∠МАВ = 100°, найдите ∠А и ∠С в
треугольнике АВС
29.
Треугольник АВС – равнобедренный, АС –основание, ВD – биссектриса, ∠СВD =


















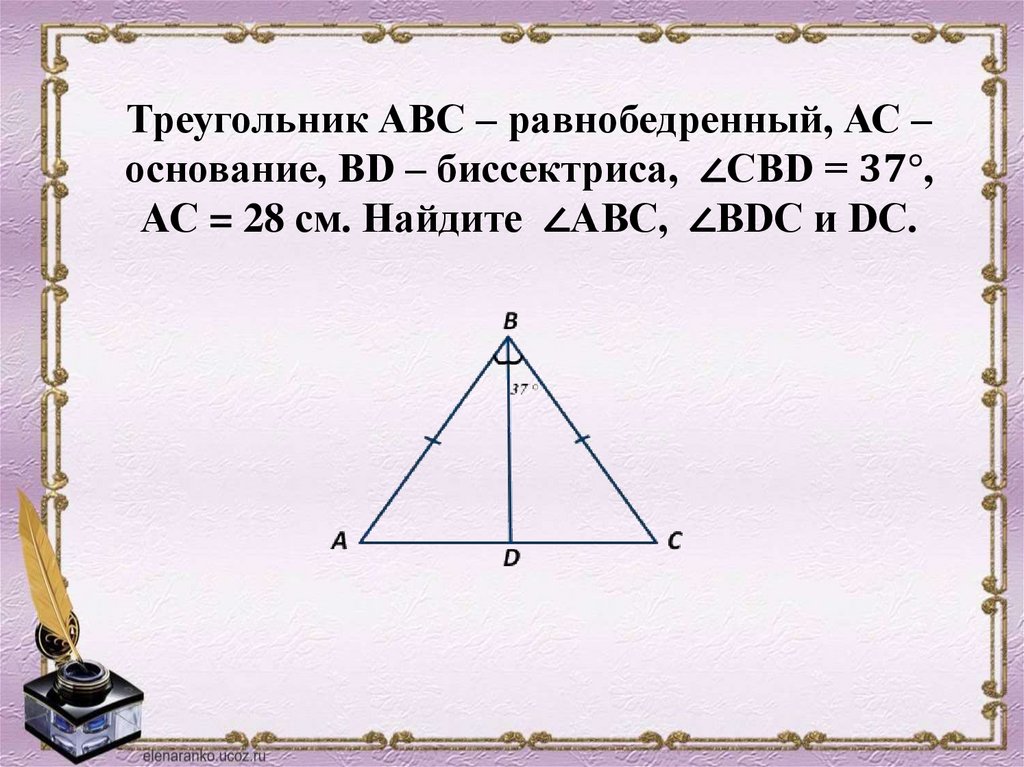




 mathematics
mathematics








