Подобие фигур

1.

04.12.2023
Классная
р а б о т а.
Подобие фигур

2.

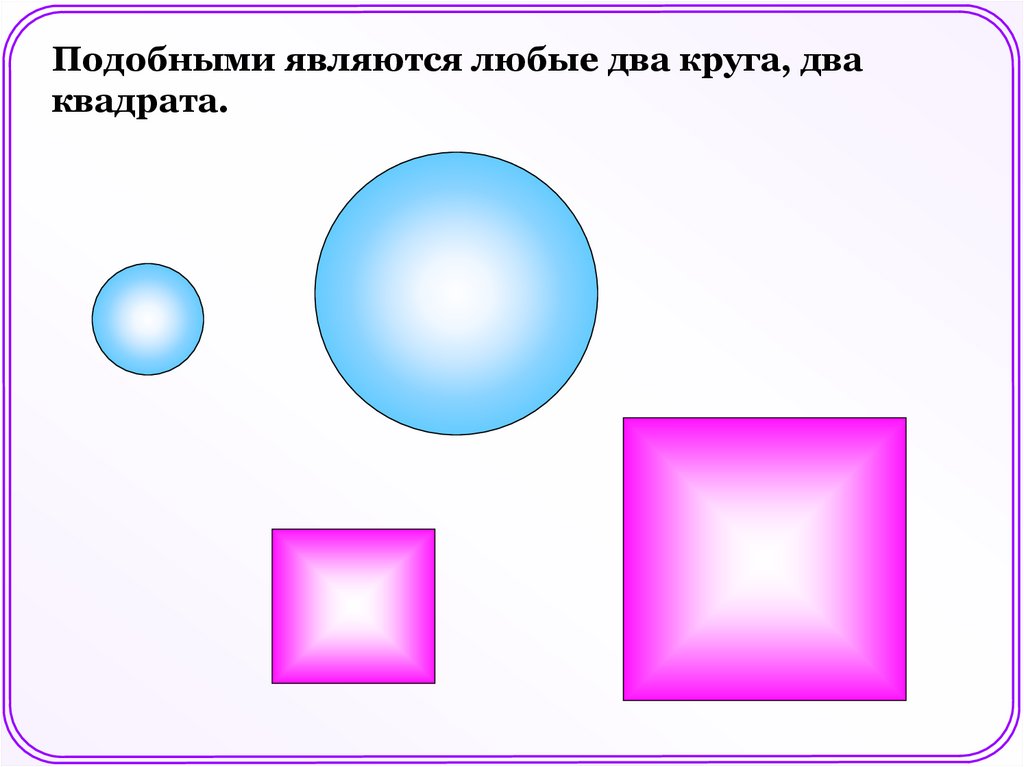
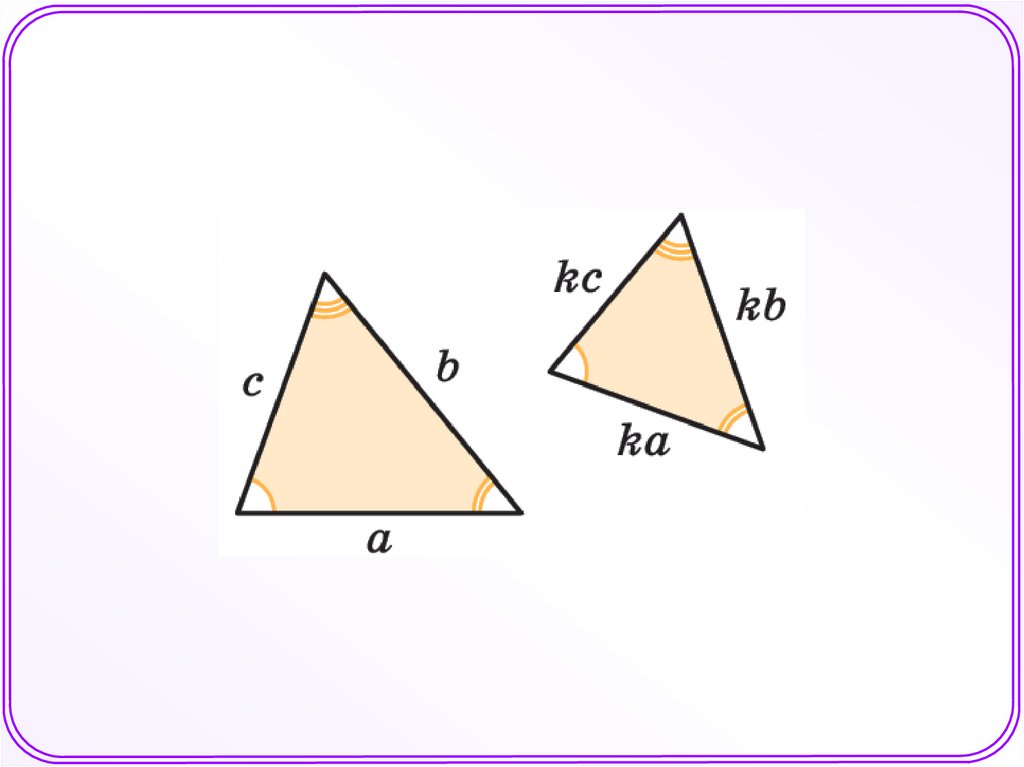
В геометрии фигуры одинаковой
формы принято называть подобными.

3.

Подобными являются любые два круга, два
квадрата.

4.

Углы при подобии не изменяются.

5.

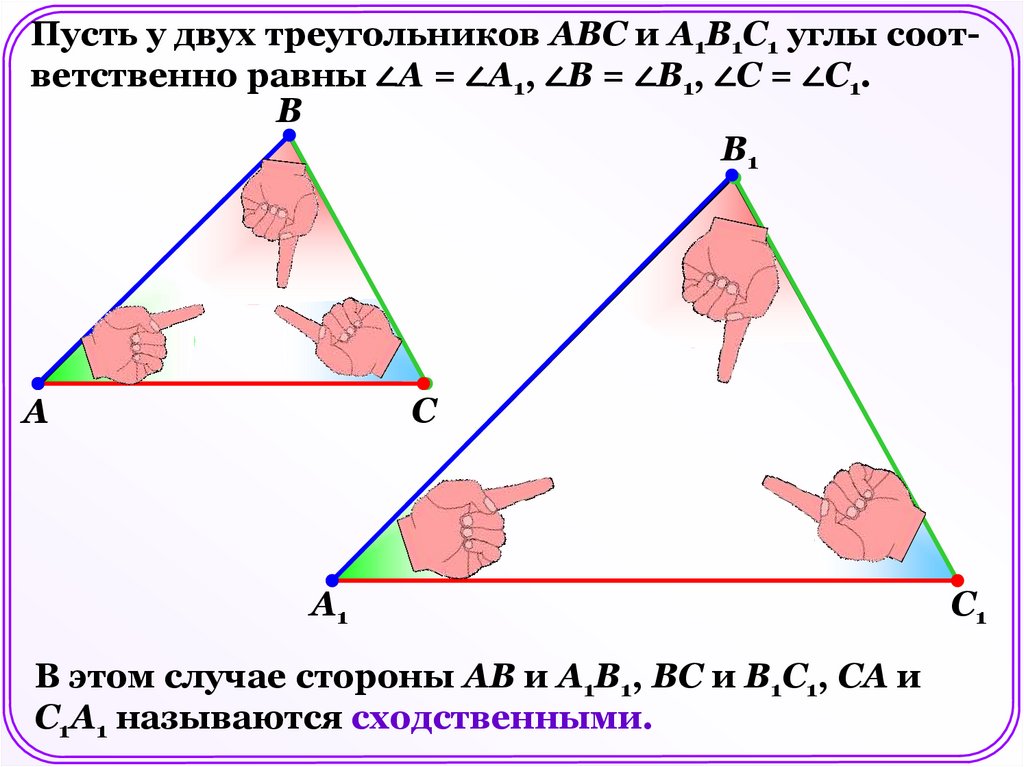
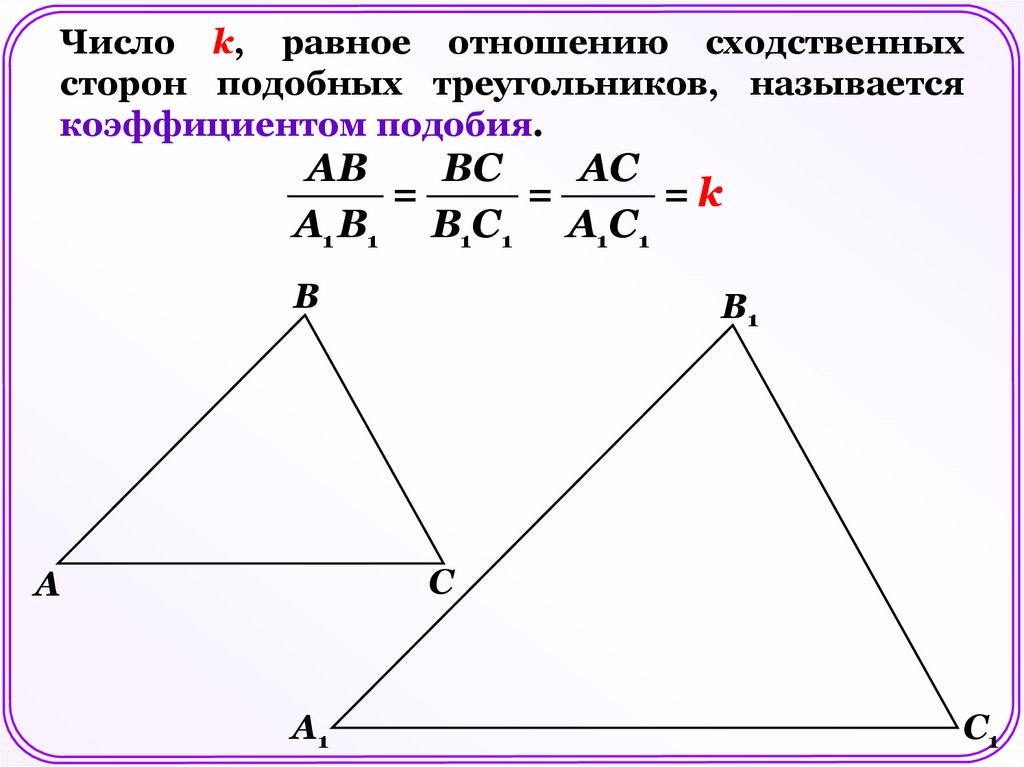
Пусть у двух треугольников АВС и А1В1С1 углы соответственно равны ∠А = ∠А1, ∠В = ∠В1, ∠С = ∠С1.
В
В1
С
А
А1
В этом случае стороны АВ и А1В1, ВС и В1С1, СА и
С1А1 называются сходственными.
С1

6.

7.

8.

Запишите равенство отношений сходственных
сторон подобных треугольников:
АВ
=
KE
ВС =
KF
АС
EF

9.

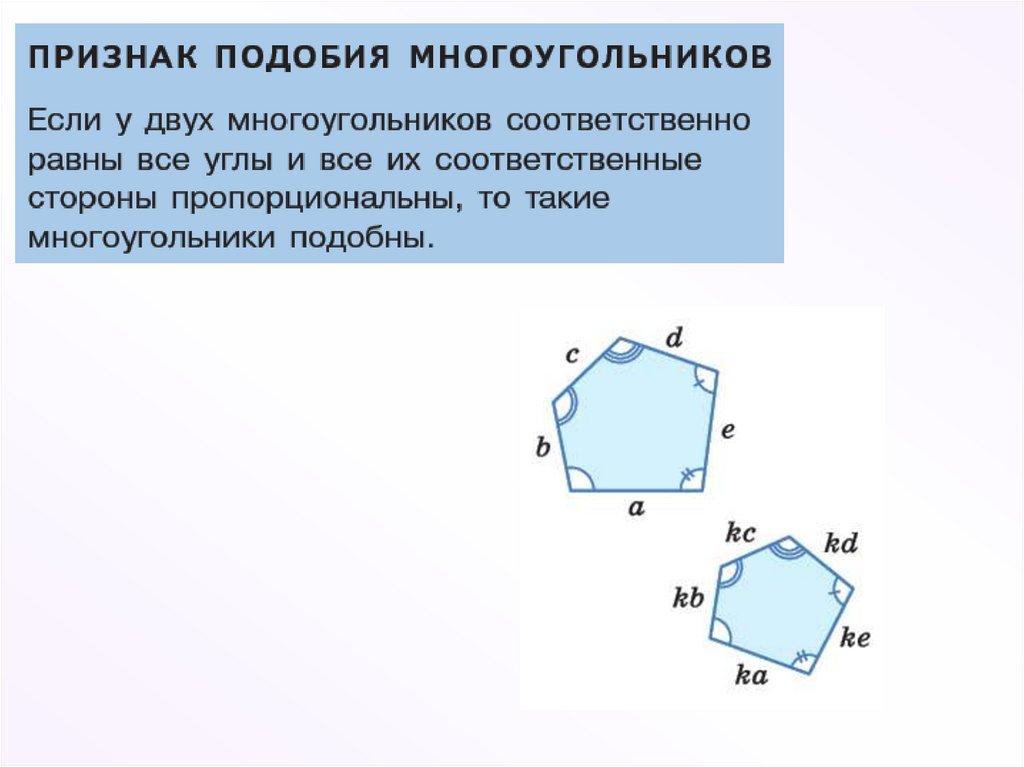
Число k, равное отношению сходственных
сторон подобных треугольников, называется
коэффициентом подобия.
АВ
ВС
АС
=
=
=k
А1 В1 В1С1 А1С1
В
В1
С
А
А1
С1

10.

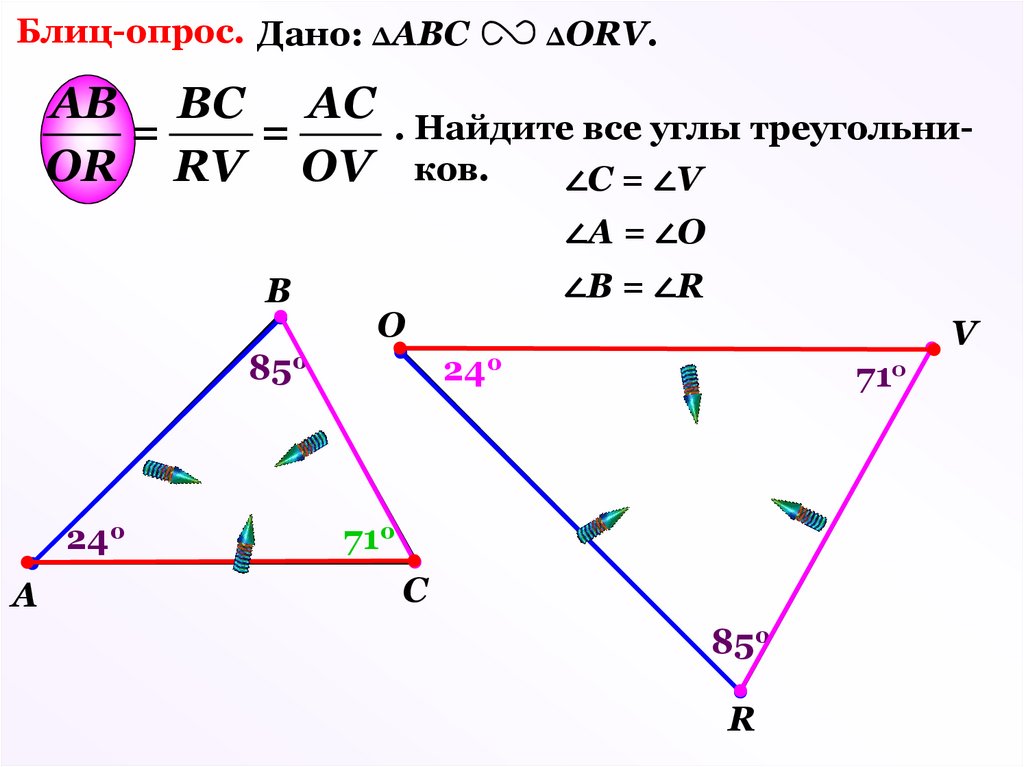
Блиц-опрос. Дано: ΔАВС
ΔОRV.
АВ ВС АС . Найдите все углы треугольни=
=
OR RV OV ков.
∠C = ∠V
∠А = ∠О
В
∠В = ∠R
O
850
240
А
V
240
71о
710
С
850
R

11.

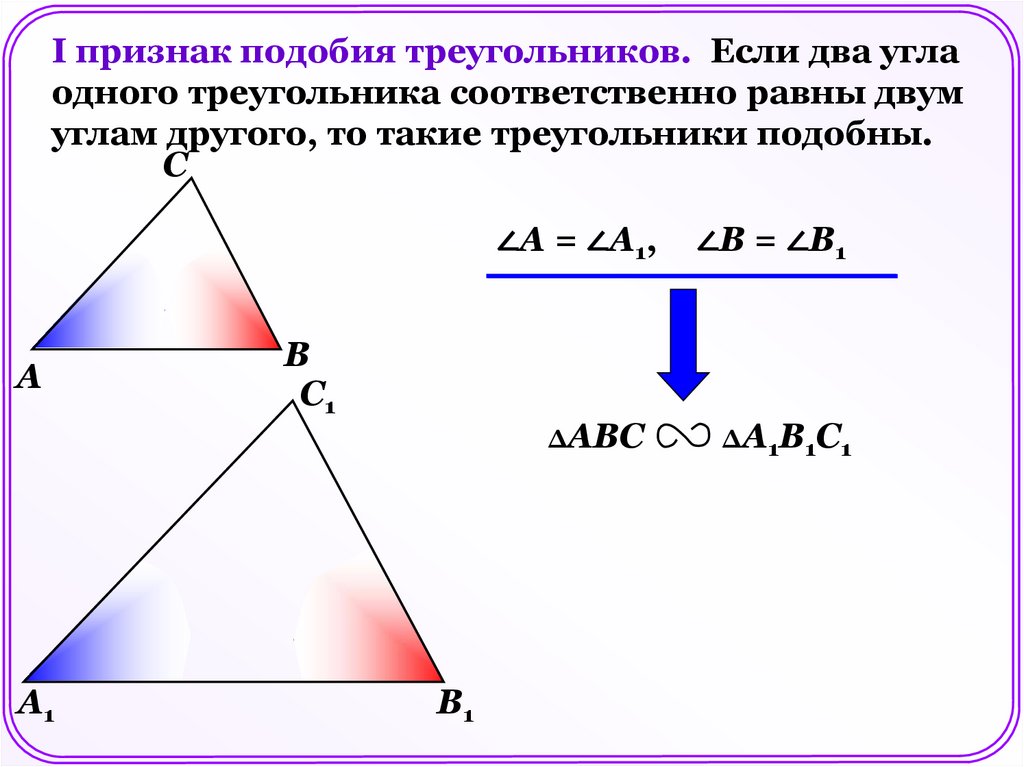
I признак подобия треугольников. Если два угла
одного треугольника соответственно равны двум
углам другого, то такие треугольники подобны.
С
А
А1
В
С1
В1
∠А = ∠А1,
∠В = ∠В1
ΔАВС
ΔА1В1С1

12.

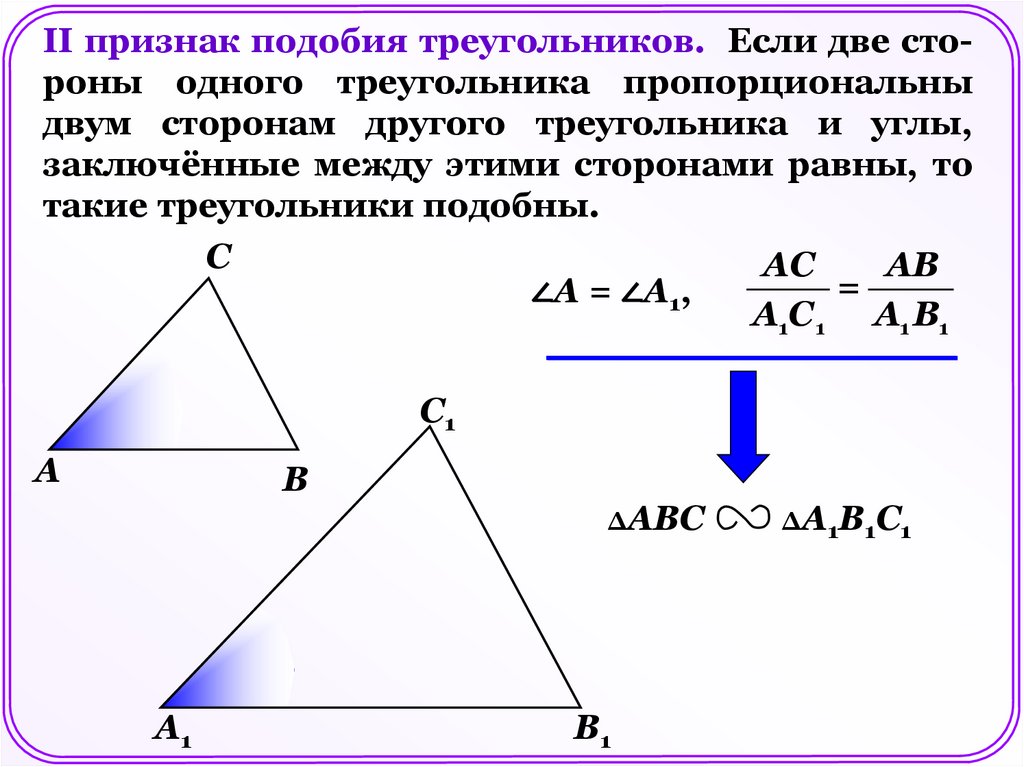
II признак подобия треугольников. Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы,
заключённые между этими сторонами равны, то
такие треугольники подобны.
С
АС
АВ
=
∠А = ∠А1,
А1С 1 A1 В1
С1
А
В
ΔАВС
А1
В1
ΔА1В1С1

13.

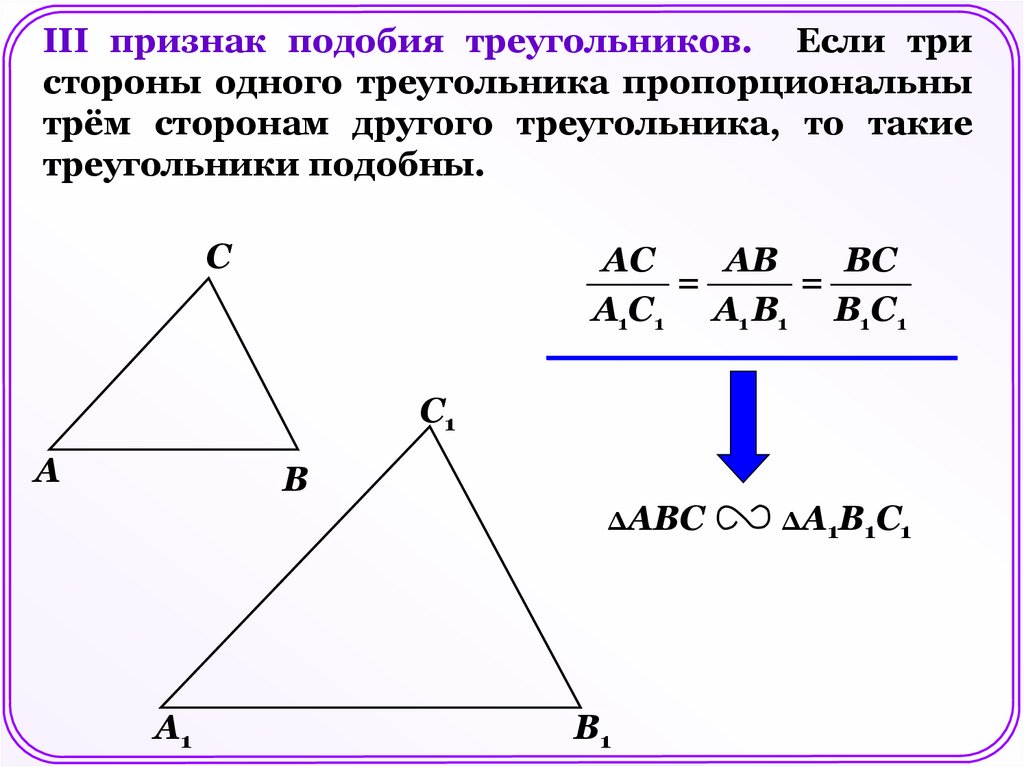
III признак подобия треугольников. Если три
стороны одного треугольника пропорциональны
трём сторонам другого треугольника, то такие
треугольники подобны.
С
АС
АВ
ВС
=
=
А1С1 A1 В1 В1С1
С1
А
В
ΔАВС
А1
В1
ΔА1В1С1

14.

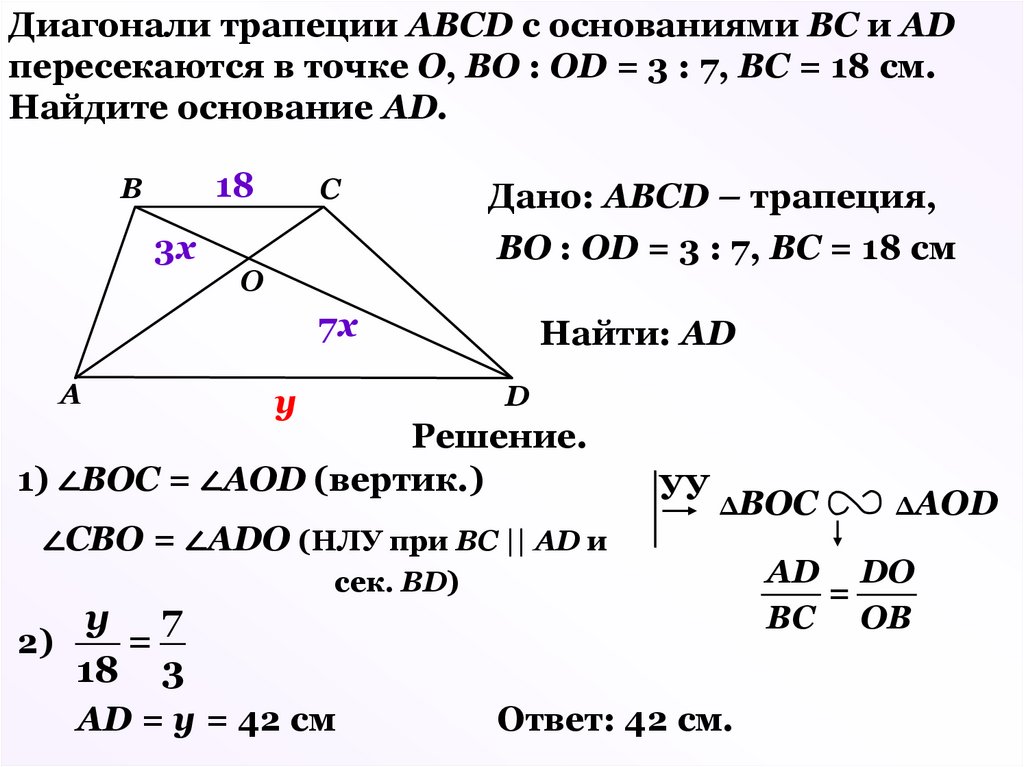
Диагонали трапеции АВСD с основаниями ВС и АD
пересекаются в точке О, ВО : ОD = 3 : 7, ВС = 18 см.
Найдите основание АD.
18
В
3х
С
О
Дано: АВСD – трапеция,
ВО : ОD = 3 : 7, ВС = 18 см
7х
А
Найти: АD
D
у
Решение.
1) ∠ВОС = ∠АОD (вертик.)
∠СВО = ∠АDО (НЛУ при ВС || АD и
у 7
=
2)
18 3
УУ ΔВОС
сек. ВD)
АD = у = 42 см
Ответ: 42 см.
ΔАОD
АD DO
=
ВC ОВ

15.

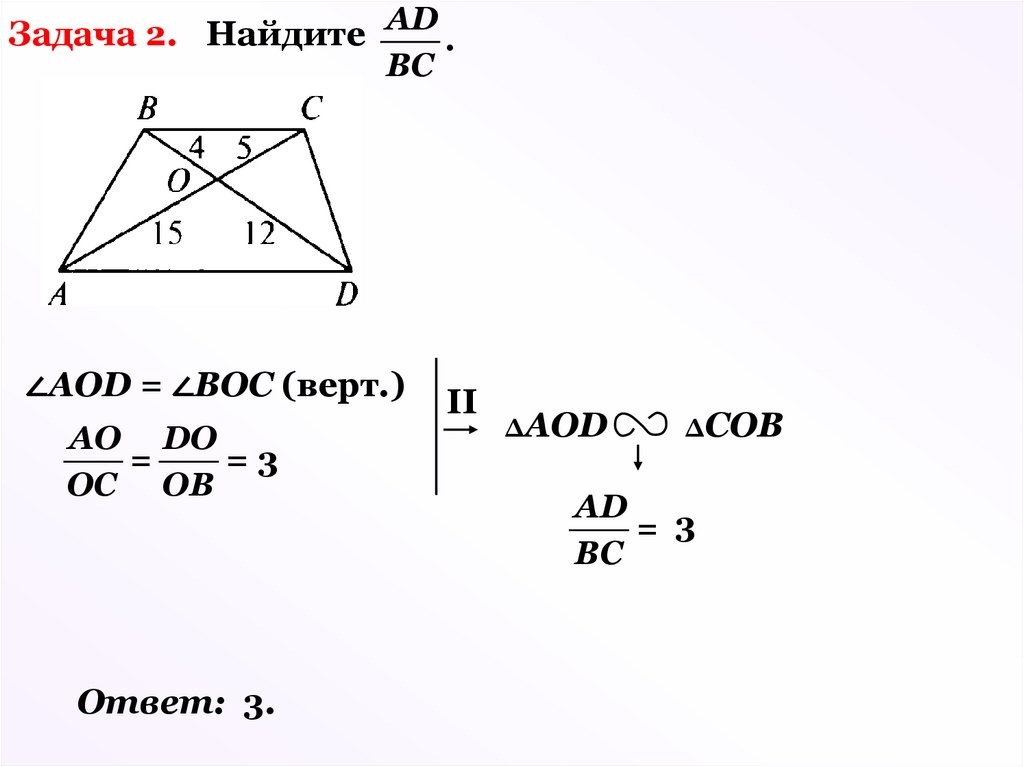
Задача 2. Найдите AD .
ВС
∠АOD = ∠ВОС (верт.)
АО DO
=
=3
ОC ОВ
Ответ: 3.
II
ΔАОD
ΔCОВ
AD
= 3
ВС

16.

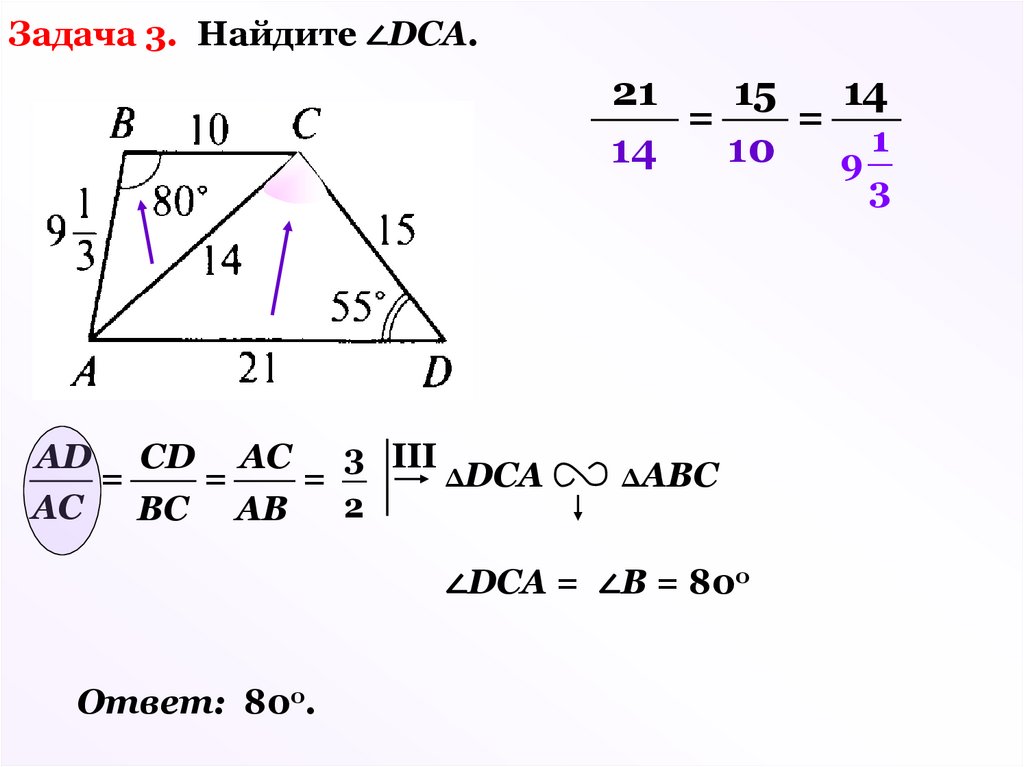
Задача 3. Найдите ∠DCA.
21
15
14
=
=
1
10
14
9
3
AD CD АС
3 III
ΔDCА
=
=
=
2
АС
ВС АВ
ΔАВС
∠DCA = ∠В = 80о
Ответ: 80о.

17.

Дано: АВ || DC,
АВ = 14, DC = 42, АС = 52
Найти: МС.
Решение.
1) АМВ СМD (верт.)
ВАМ DСМ (НЛУ при АВ || DC и сек. АС)
Значит, ΔАМВ : ΔСМD по двум углам.

18.

Дано: АВ || DC,
14
АВ = 14, DC = 42, АС = 52
52 – х
х
Найти: МС.
42
Решение.
АМ АВ
2) Значит,
=
МС DC
52 х 14
=
х
42

19.

52 х 14
=
х
42
52 х 1
=
х
3
х≠0
3(52 – х) = х
156 – 3х = х
4х = 156
х = 39
МС = 39
Ответ: 39.

20.

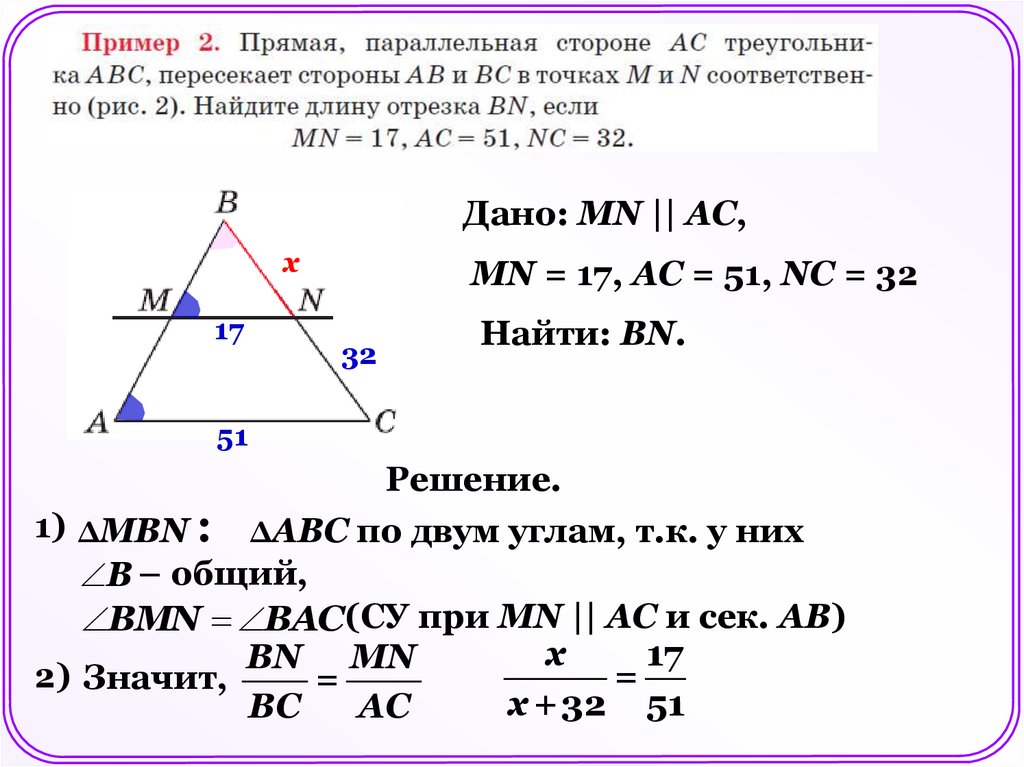
Дано: MN || AC,
х
17
MN = 17, AC = 51, NС = 32
32
Найти: BN.
51
Решение.
1) ΔМВN : ΔАВС по двум углам, т.к. у них
В – общий,
ВМN BAC(СУ при MN || АC и сек. АВ)
х
17
BN MN
2) Значит,
=
=
х + 32 51
BС
AC

21.

х
17
=
х + 32 51
х
1
=
х≠0
х +32 3
3х = х + 32
2х = 32
х = 16
ВN = 16
Ответ: 16.