Similar presentations:
Углы. Произвольный треугольник. Прототип 15 задания ОГЭ
1.
Прототип 15задания ОГЭ.
Углы.
Произвольный
треугольник.
2.
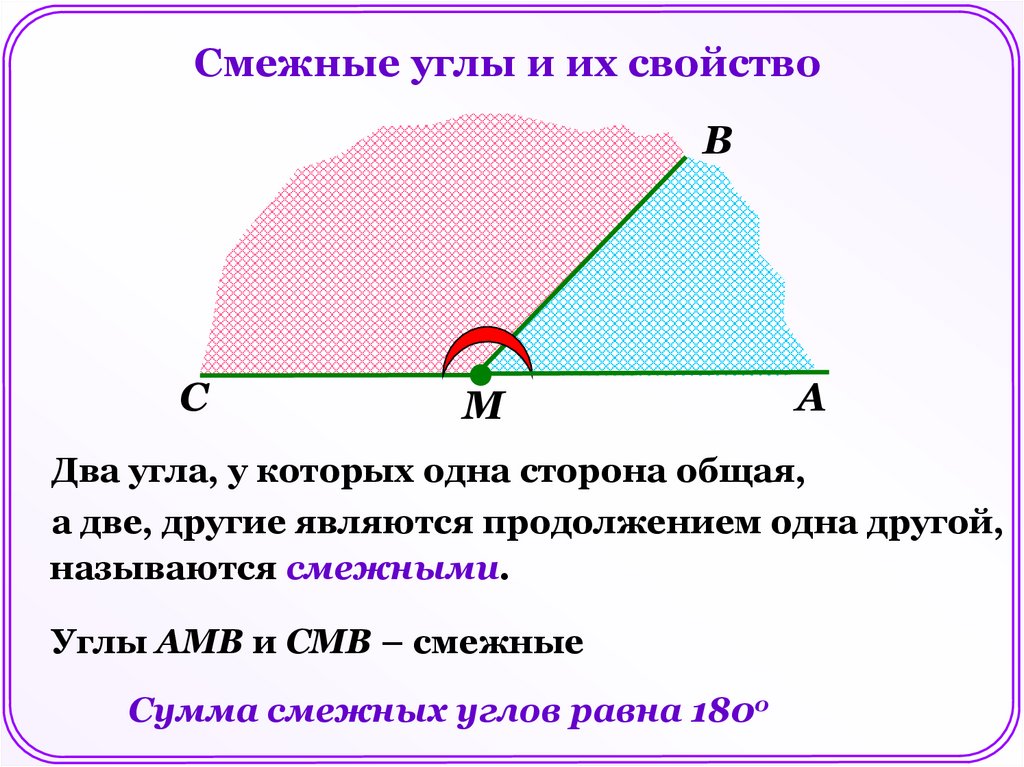
Смежные углы и их свойствоВ
С
М
А
Два угла, у которых одна сторона общая,
а две, другие являются продолжением одна другой,
называются смежными.
Углы АМВ и СМВ – смежные
Сумма смежных углов равна 180о
3.
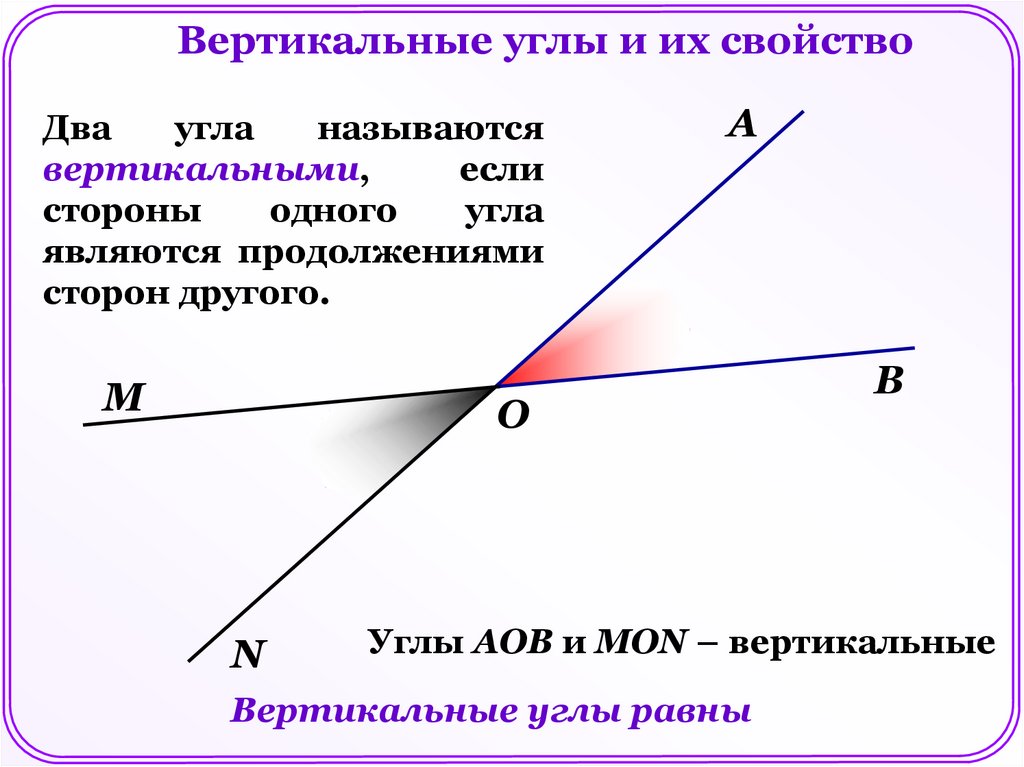
Вертикальные углы и их свойствоДва
угла
называются
вертикальными,
если
стороны
одного
угла
являются продолжениями
сторон другого.
М
А
О
N
В
Углы АОВ и MON – вертикальные
Вертикальные углы равны
4.
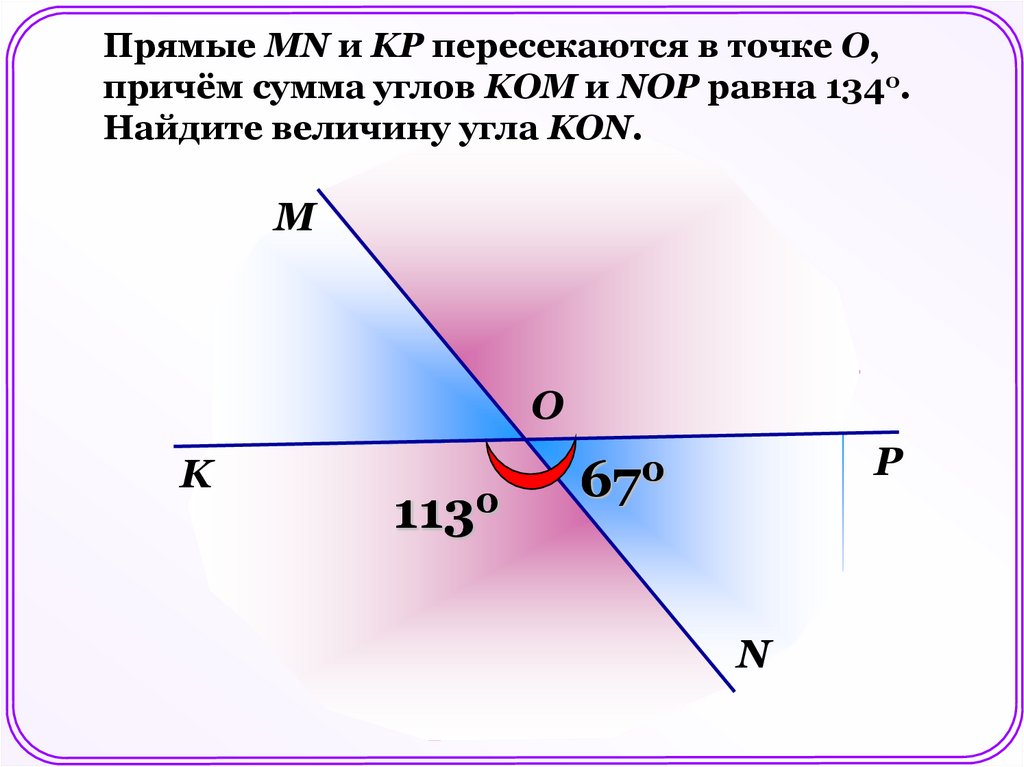
Прямые MN и KР пересекаются в точке О,причём сумма углов KOM и NOP равна 134о.
Найдите величину угла KON.
М
О
K
1130
Р
670
N
5.
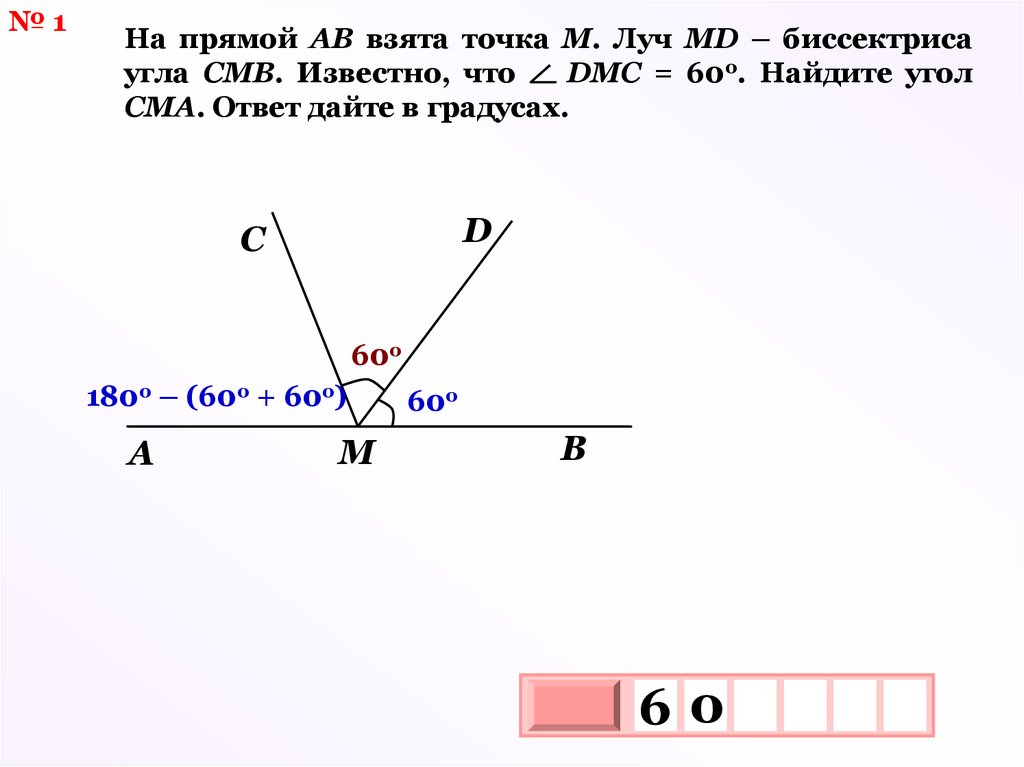
№1На прямой АВ взята точка М. Луч MD – биссектриса
угла СМВ. Известно, что
DМС = 60о. Найдите угол
СМА. Ответ дайте в градусах.
D
C
60о
180о – (60о + 60о)
A
M
60о
B
60
3
10 х
х
6.
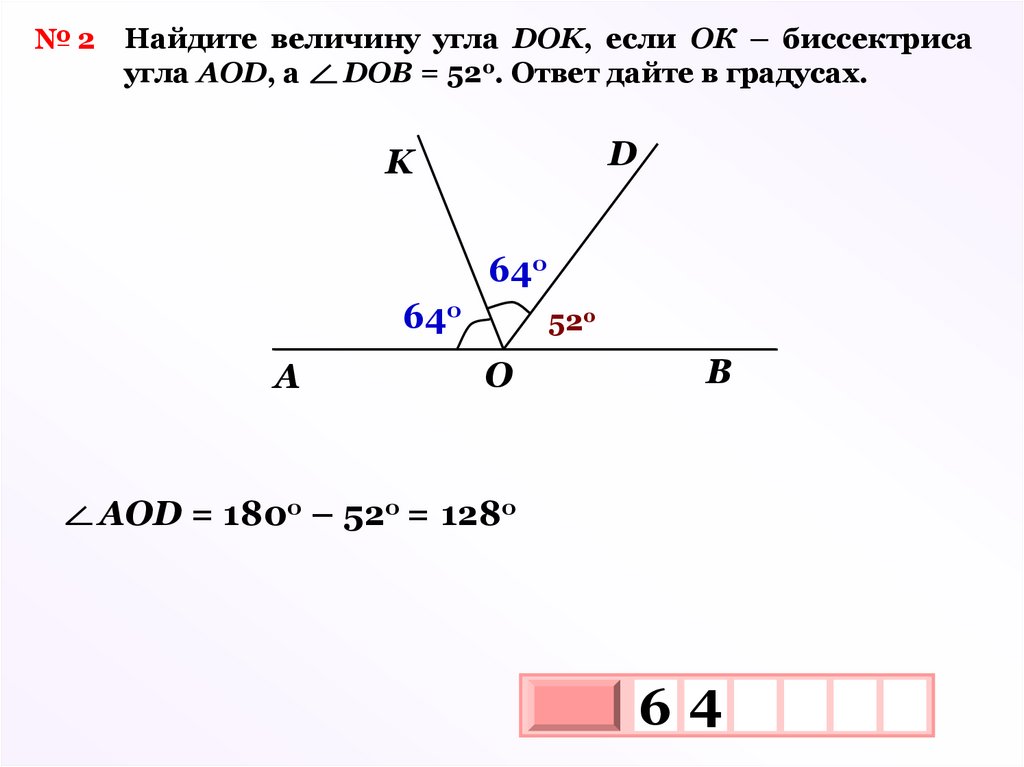
№ 2 Найдите величину угла DOK, если ОК – биссектрисаугла АОD, а
DOB = 52о. Ответ дайте в градусах.
D
K
64о
64о
A
52о
O
B
АОD = 180о – 52о = 128о
64
3
10 х
х
7.
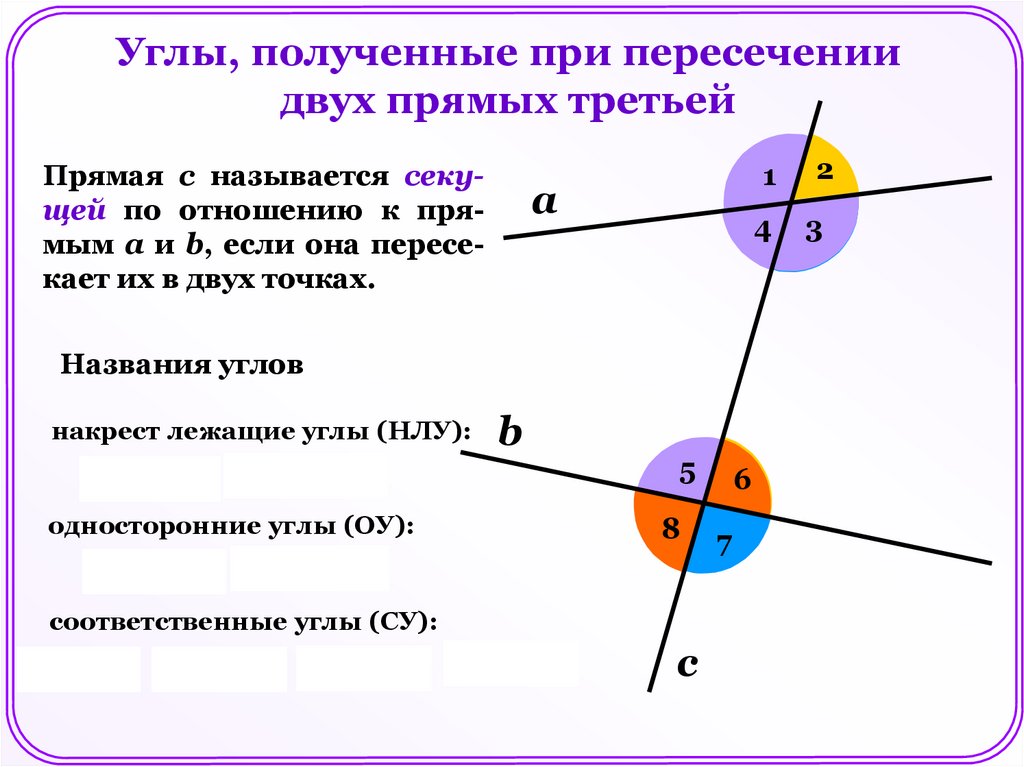
Углы, полученные при пересечениидвух прямых третьей
Прямая с называется секущей по отношению к прямым а и b, если она пересекает их в двух точках.
а
Названия углов
накрест лежащие углы (НЛУ):
3 и 5, 4 и 6
b
односторонние углы (ОУ):
5
8
4 и 5, 3 и 6
соответственные углы (СУ):
1 и 5, 4 и 8, 2 и 6, 3 и 7
с
6
7
1
2
4
3
8.
ba
1 2
3 4
c
d
10
11 12
9
5 6
7 8
13
15
14
16
9.
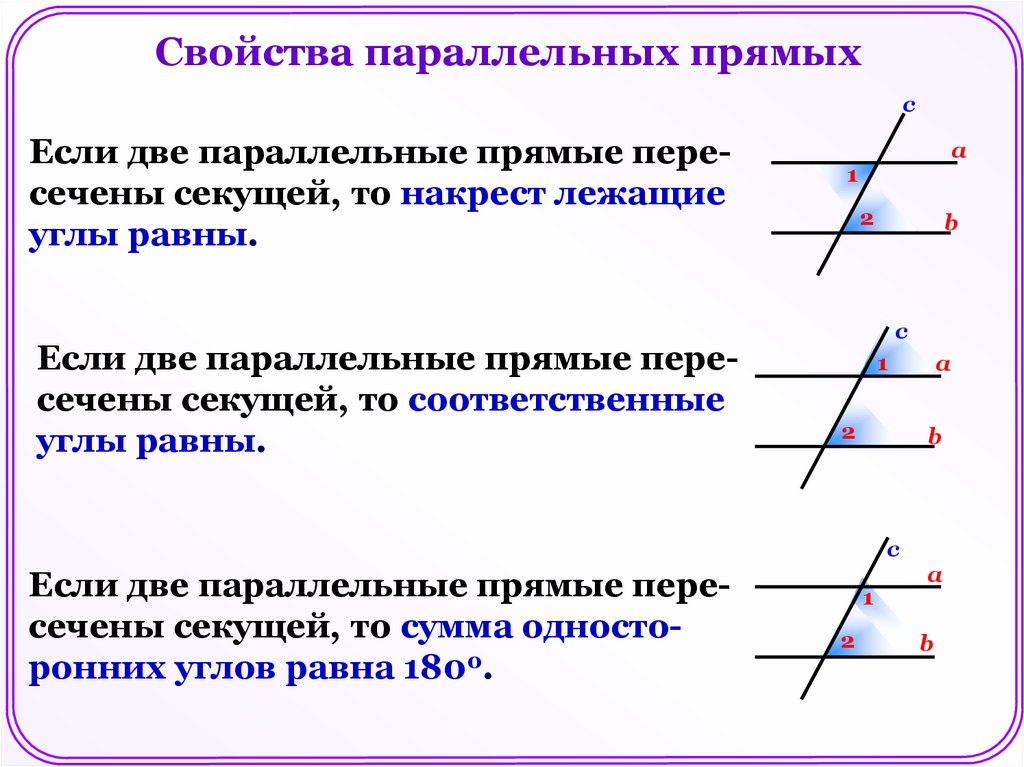
Свойства параллельных прямыхc
Если две параллельные прямые пересечены секущей, то накрест лежащие
углы равны.
Если две параллельные прямые пересечены секущей, то соответственные
углы равны.
а
1
2
b
c
1
2
b
c
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 1800.
1
2
а
а
b
10.
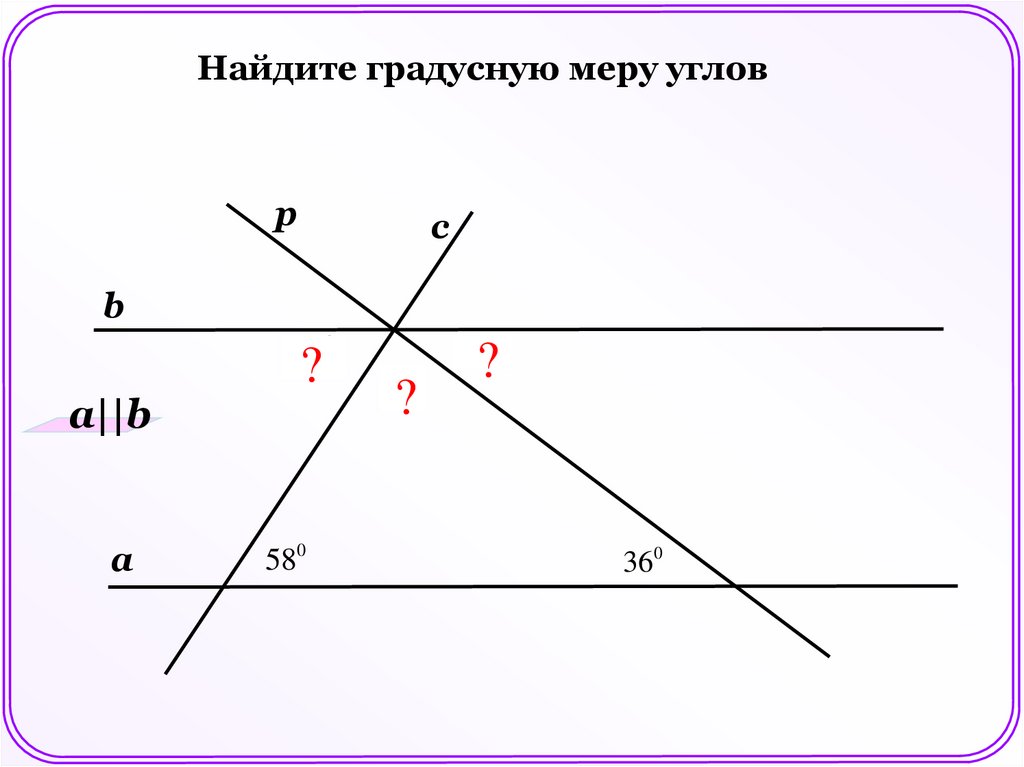
Найдите градусную меру угловp
c
b
580
a||b
a
?
580
860
?
360
?
360
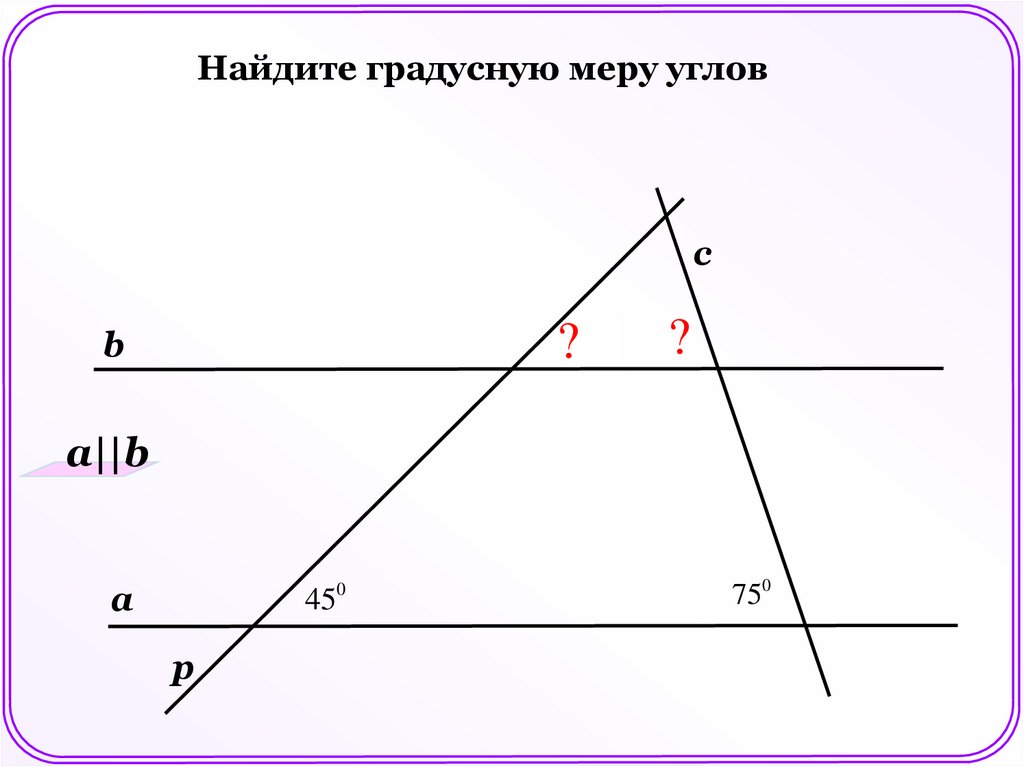
11.
Найдите градусную меру угловc
?45
b
0
?
750
a||b
a
45
p
0
750
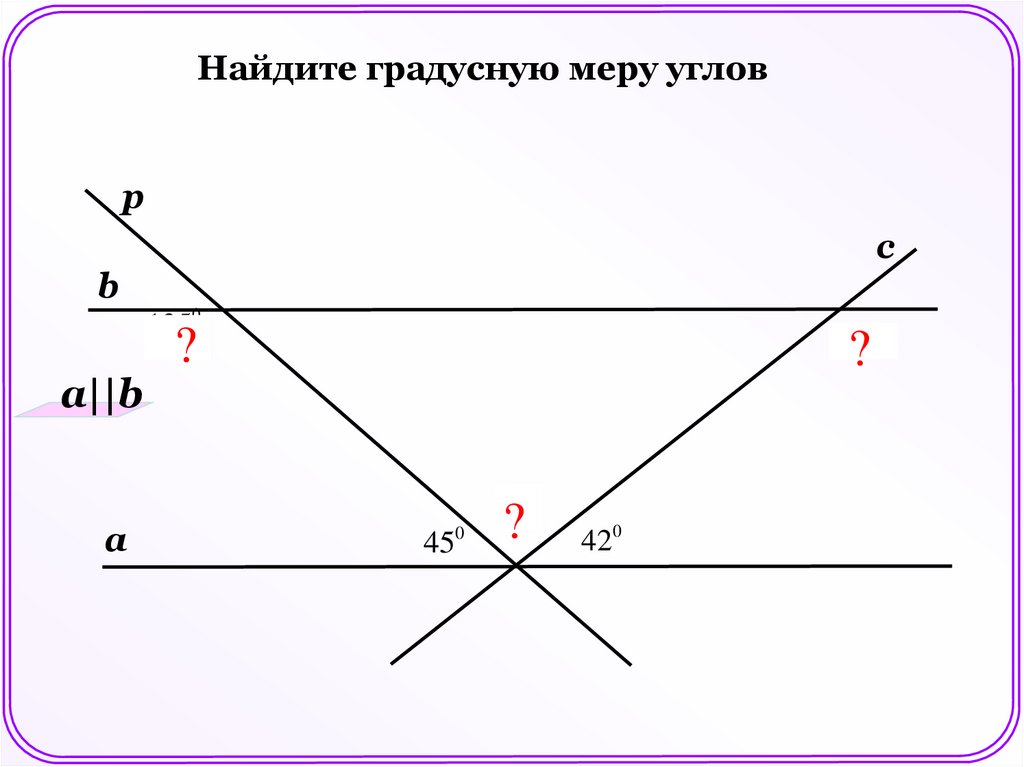
12.
Найдите градусную меру угловp
c
b
1350
a||b
a
1380
?
?
450
930
?
420
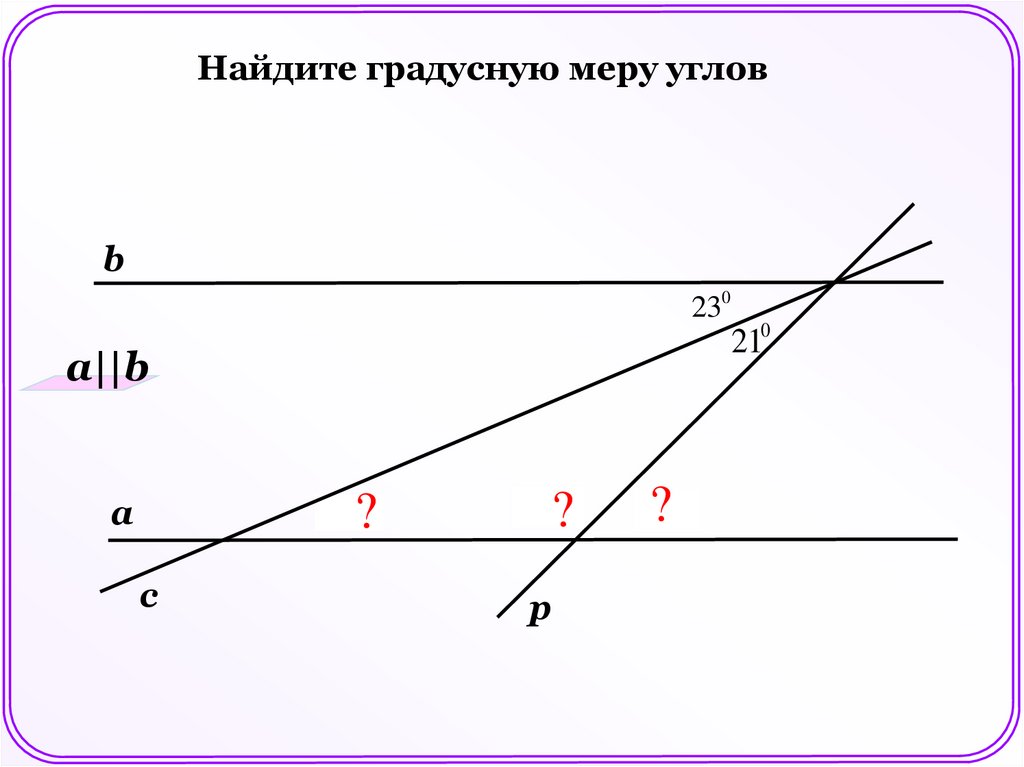
13.
Найдите градусную меру угловb
230
a||b
?
a
230
c
?
1360
p
?
440
210
14.
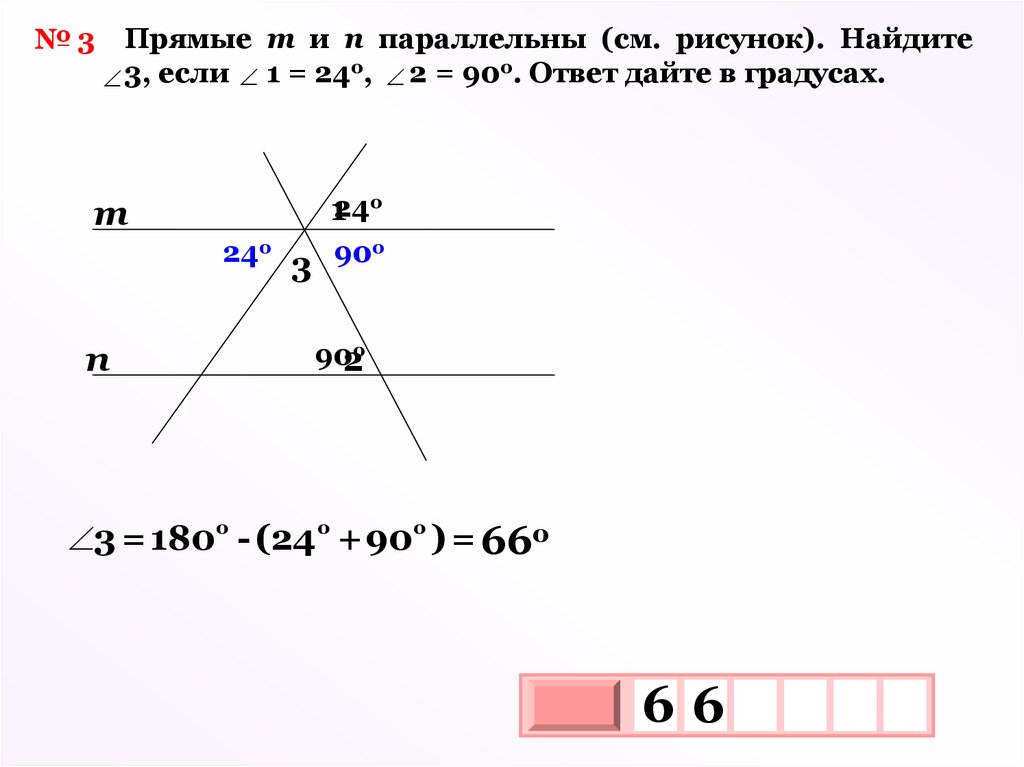
№ 3 Прямые m и n параллельны (см. рисунок). Найдитео
о
3, если 1 = 24 , 2 = 90 . Ответ дайте в градусах.
m
124о
24о 3 90о
n
902о
3 = 180o - (24o +90o ) = 66o
66
3
10 х
х
15.
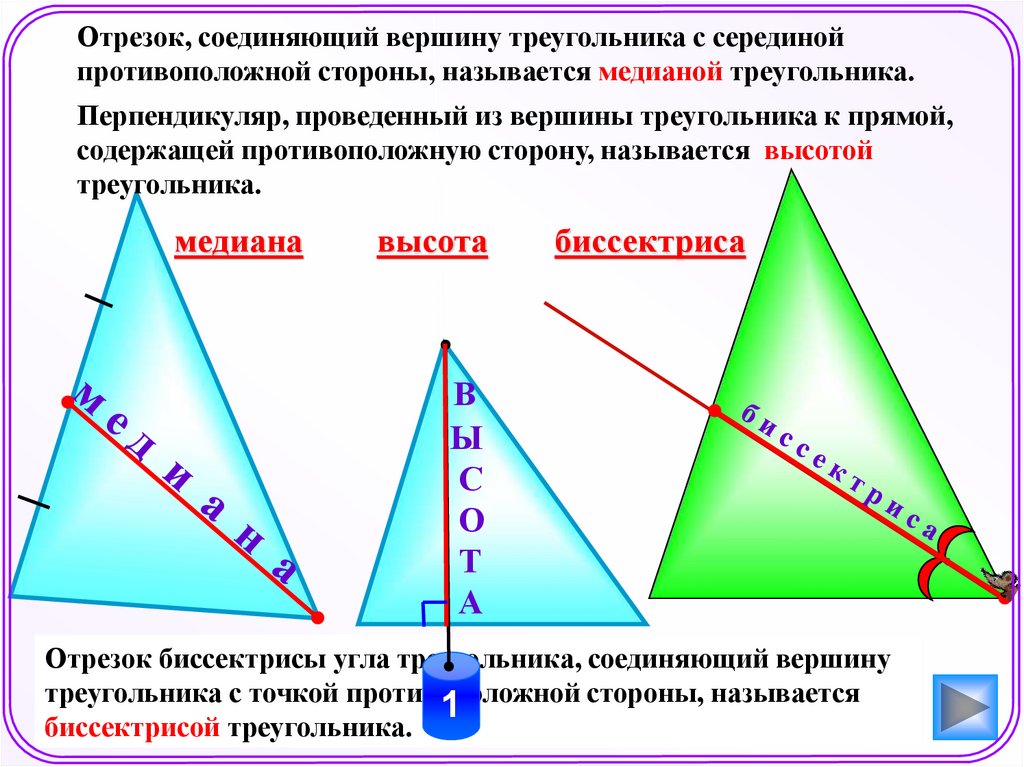
Отрезок, соединяющий вершину треугольника с серединойпротивоположной стороны, называется медианой треугольника.
Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой
треугольника.
медиана
высота
биссектриса
В
Ы
С
О
Т
А
Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны, называется
1
биссектрисой треугольника.
16.
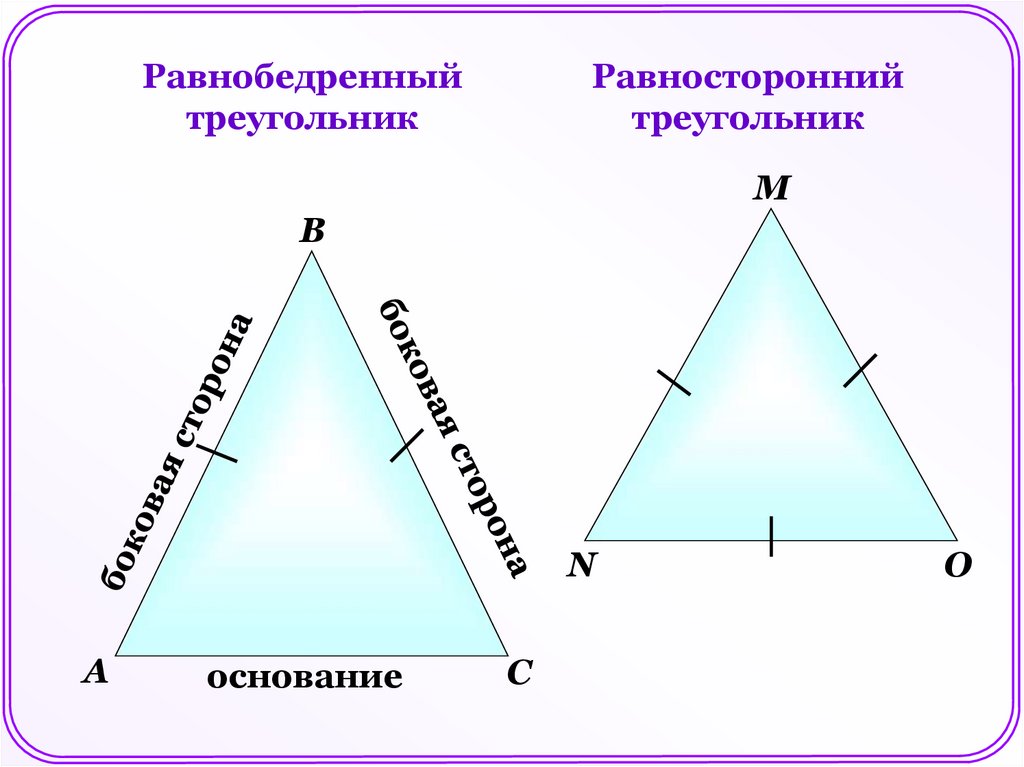
Равнобедренныйтреугольник
Равносторонний
треугольник
М
В
N
А
основание
С
О
17.
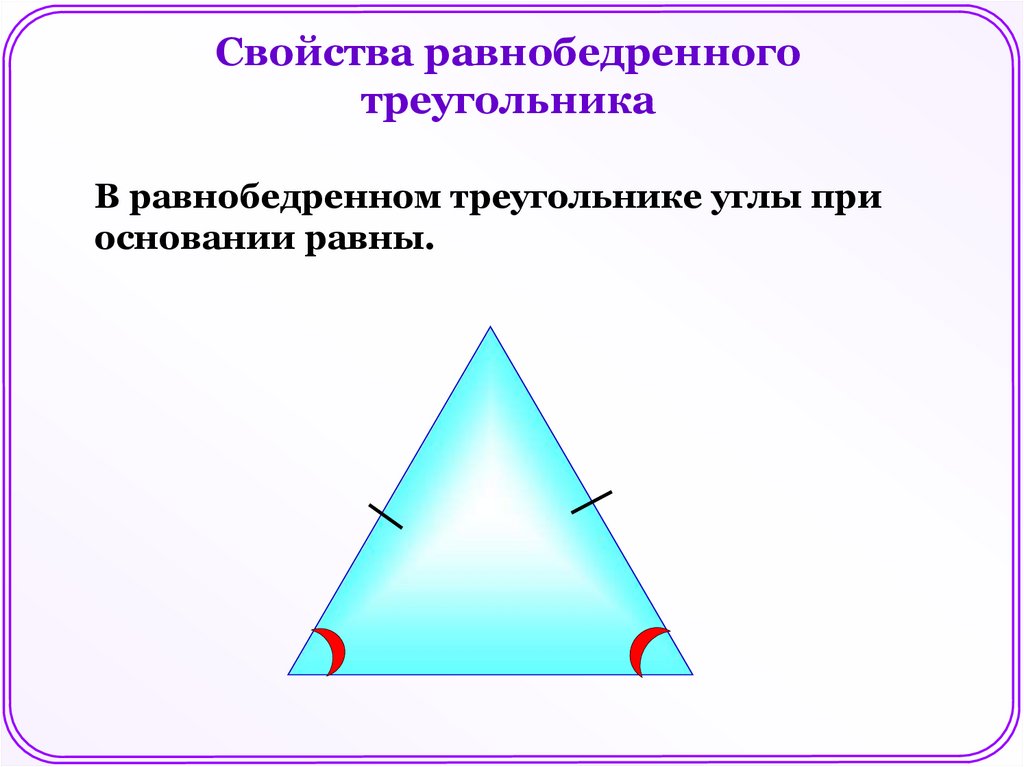
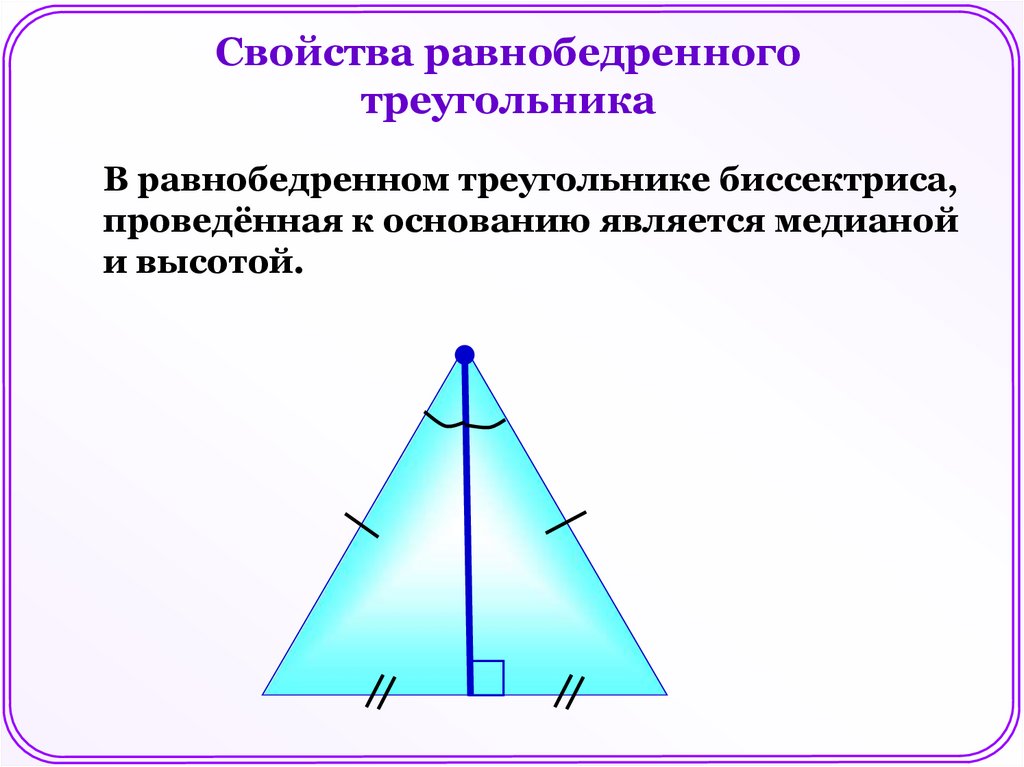
Свойства равнобедренноготреугольника
В равнобедренном треугольнике углы при
основании равны.
18.
Свойства равнобедренноготреугольника
В равнобедренном треугольнике биссектриса,
проведённая к основанию является медианой
и высотой.
19.
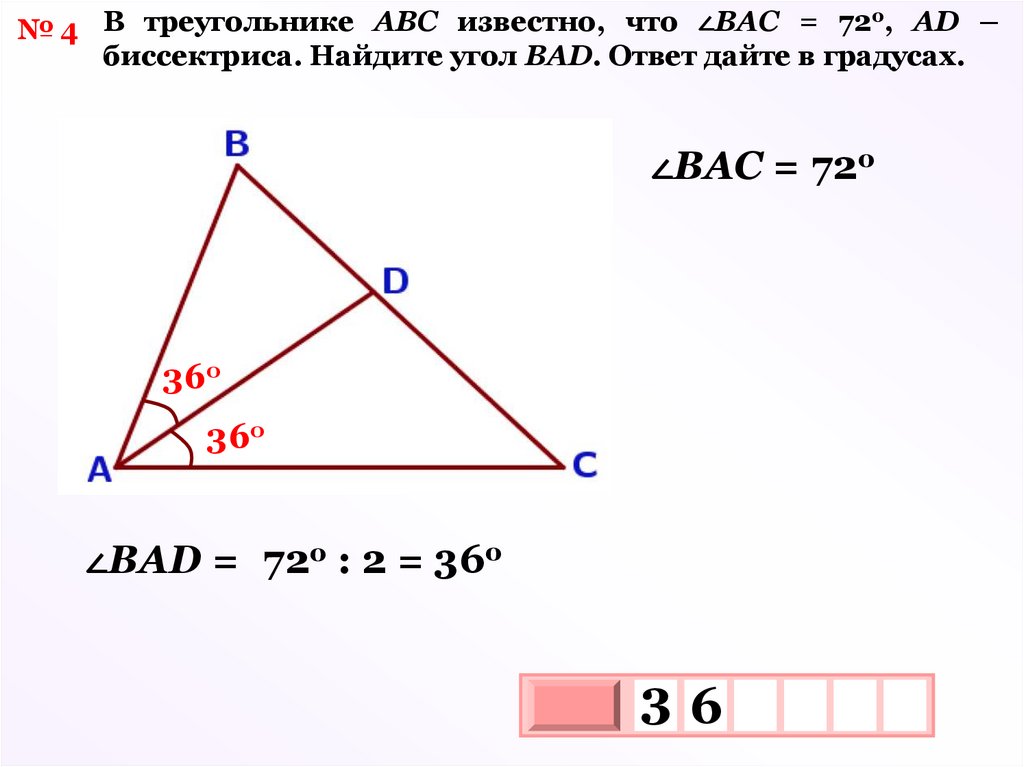
о№ 4 В треугольнике АВС известно, что ∠ВАС = 72 , AD –
биссектриса. Найдите угол ВАD. Ответ дайте в градусах.
∠ВАС = 72о
36о
36о
∠ВАD = 72о : 2 = 36о
36
3
10 х
х
20.
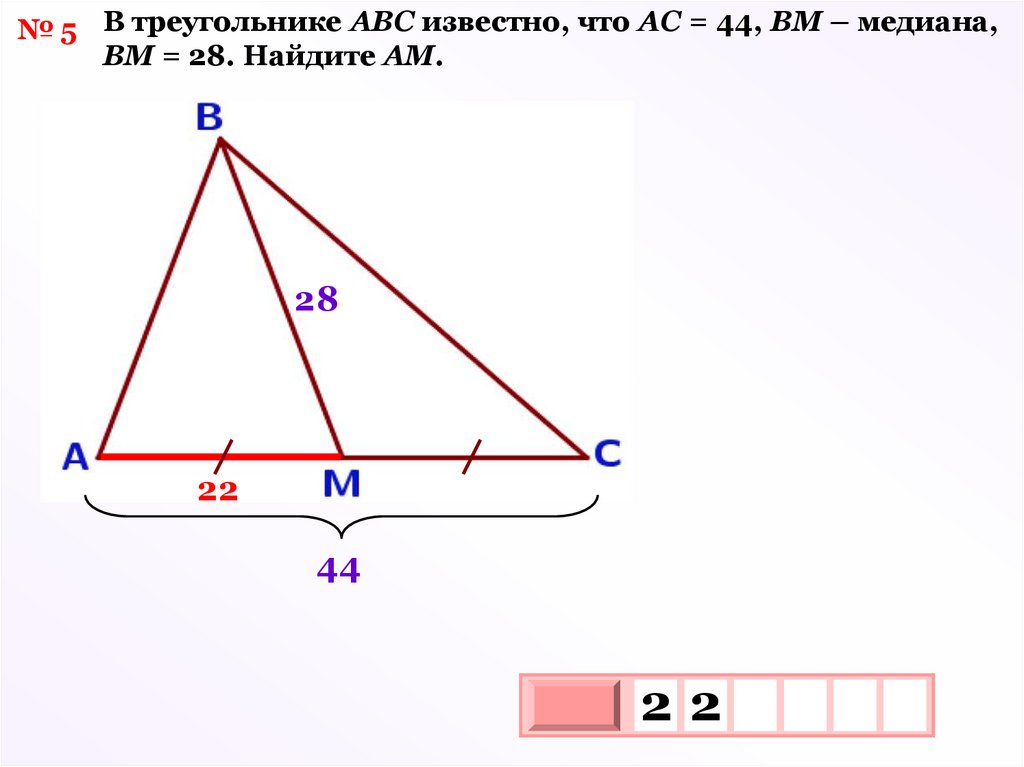
№ 5 В треугольнике АВС известно, что АС = 44, ВМ – медиана,ВМ = 28. Найдите АМ.
28
22
44
22
3
10 х
х
21.
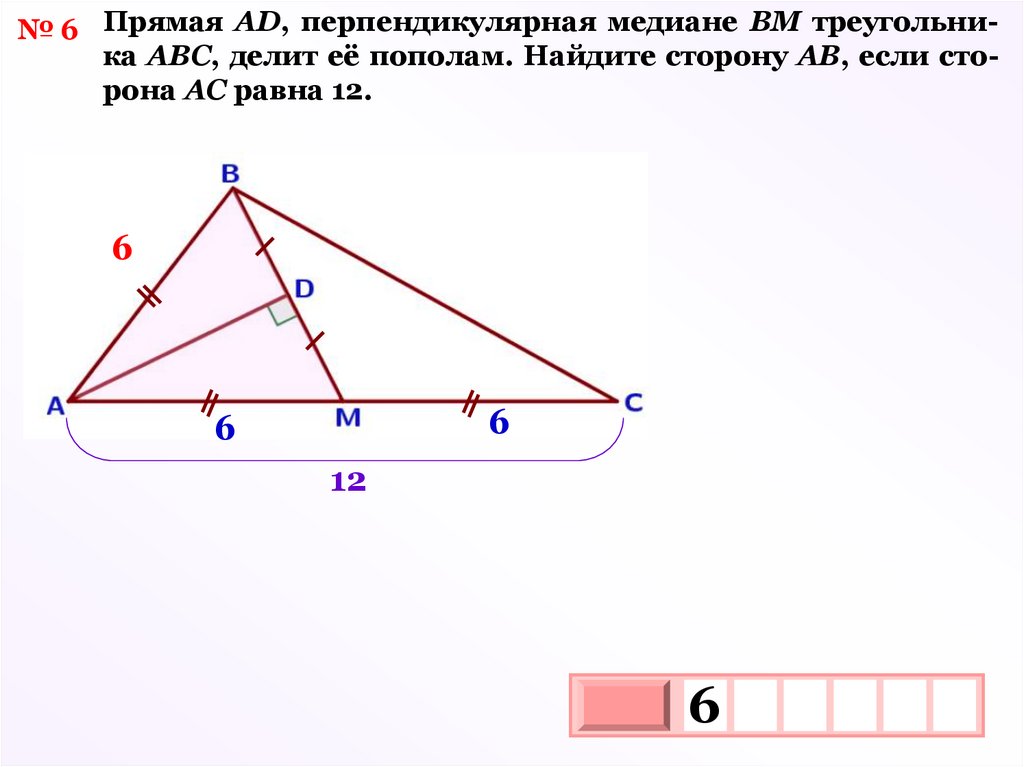
№ 6 Прямая АD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 12.6
6
6
12
6
3
10 х
х
22.
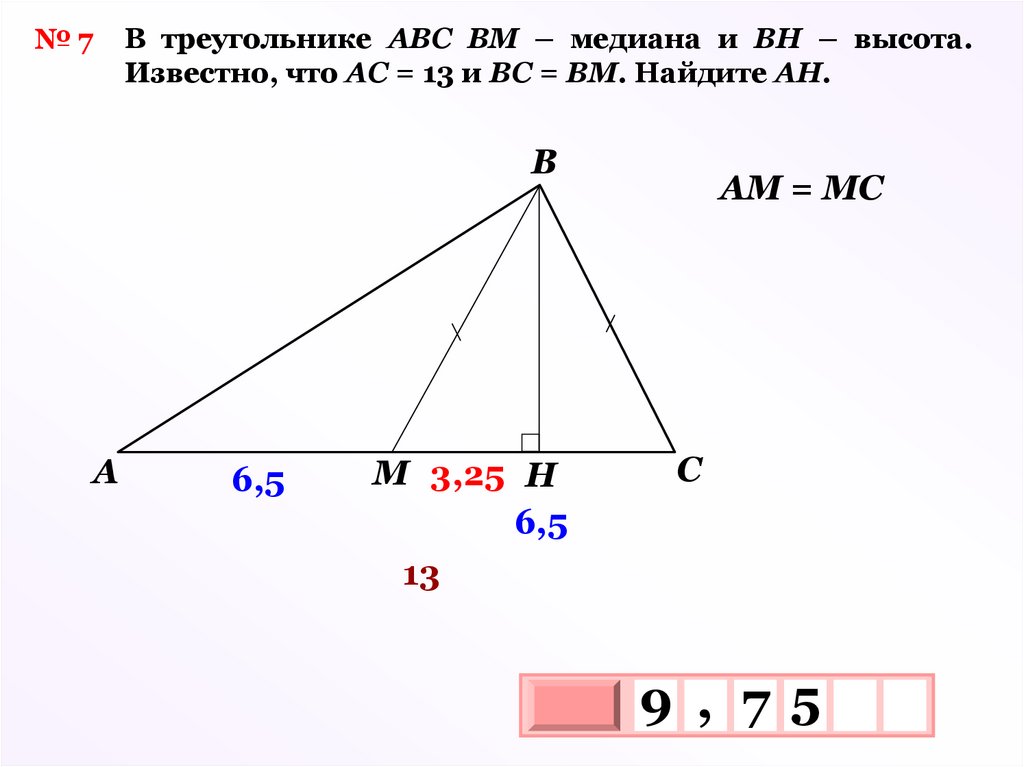
№7В треугольнике АВС ВМ – медиана и ВН – высота.
Известно, что АС = 13 и ВС = ВМ. Найдите АН.
B
A
6,5
M 3,25 H
6,5
13
АМ = МС
C
9 , 75
3
10 х
х
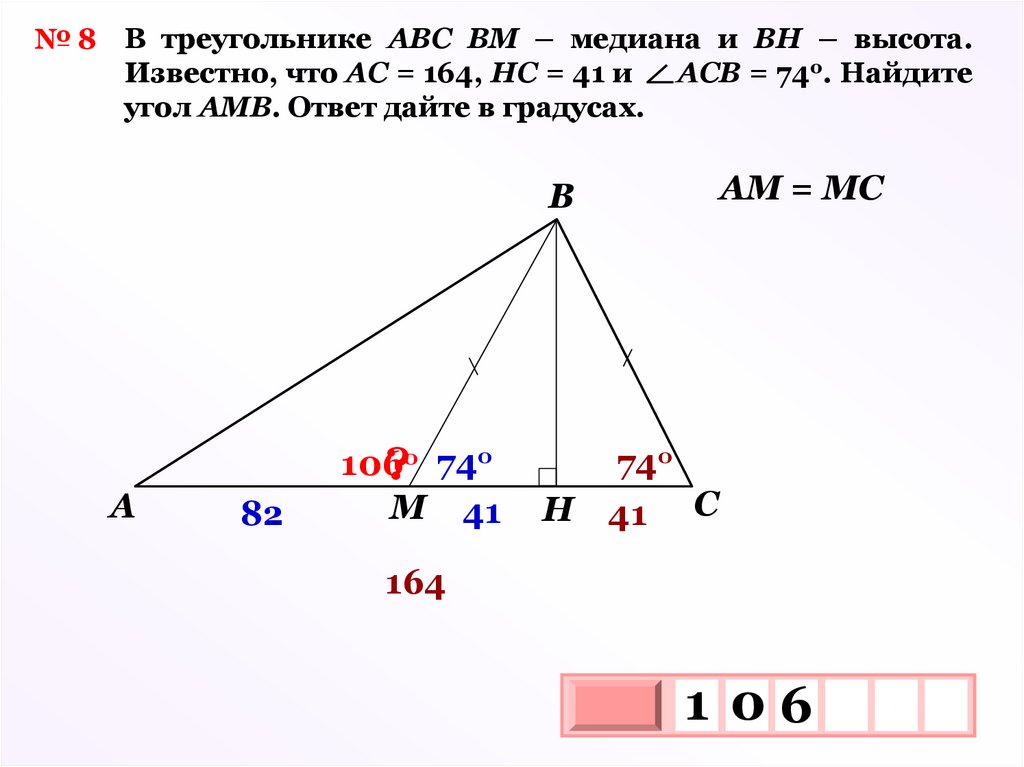
23.
№ 8 В треугольнике АВС ВМ – медиана и ВН – высота.Известно, что АС = 164, НС = 41 и
АСВ = 74о. Найдите
угол АМВ. Ответ дайте в градусах.
АМ = МС
B
A
82
106
?о 74о
M 41
74о
H
41
C
164
1 06
3
10 х
х
24.
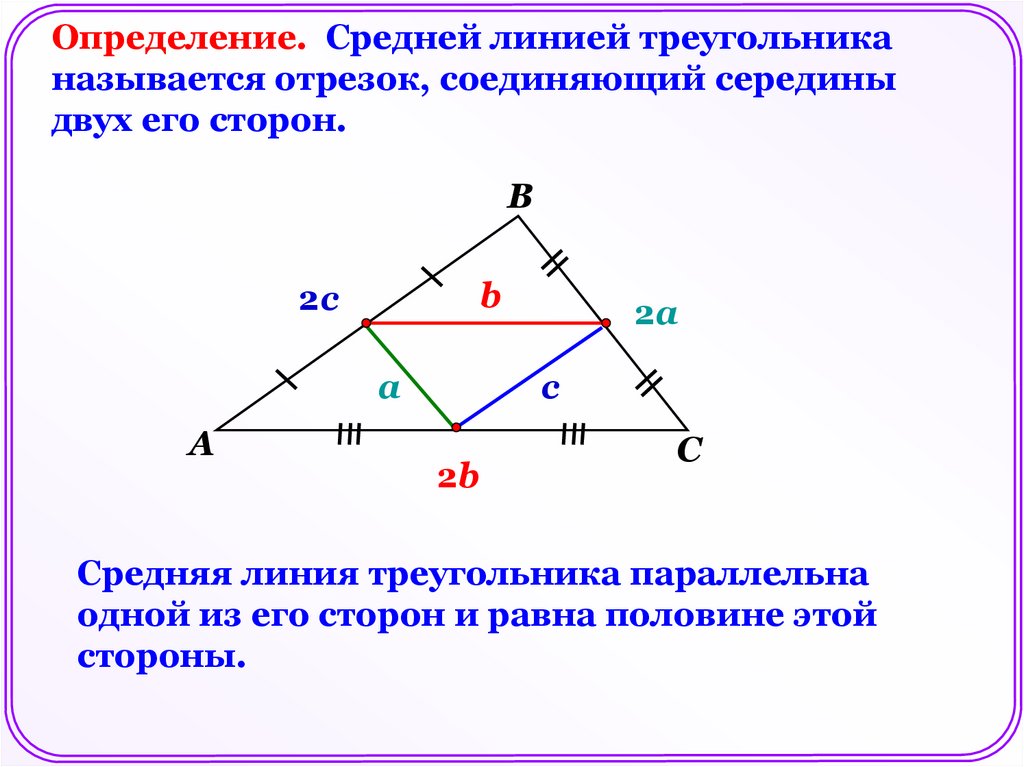
Определение. Средней линией треугольниканазывается отрезок, соединяющий середины
двух его сторон.
В
b
2c
а
А
2а
c
2b
С
Средняя линия треугольника параллельна
одной из его сторон и равна половине этой
стороны.
25.
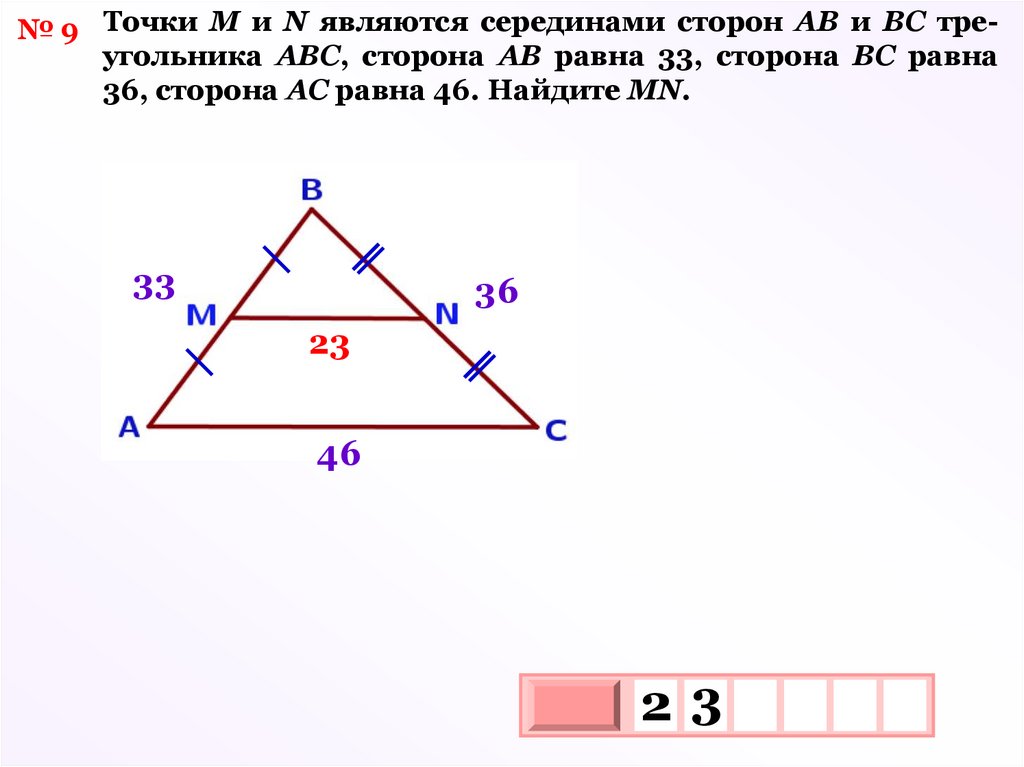
№ 9 Точки М и N являются серединами сторон АВ и ВС треугольника АВС, сторона АВ равна 33, сторона ВС равна36, сторона АС равна 46. Найдите МN.
33
36
23
46
23
3
10 х
х
26.
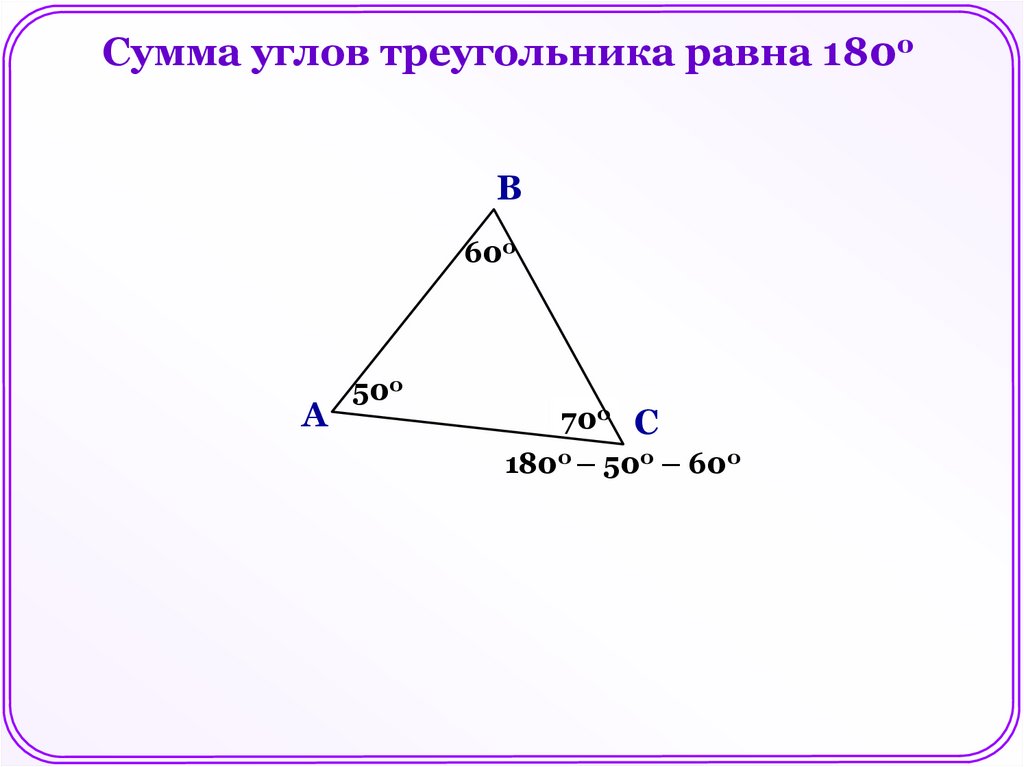
Сумма углов треугольника равна 180оВ
600
А
500
70
?0 С
1800 – 500 – 600
27.
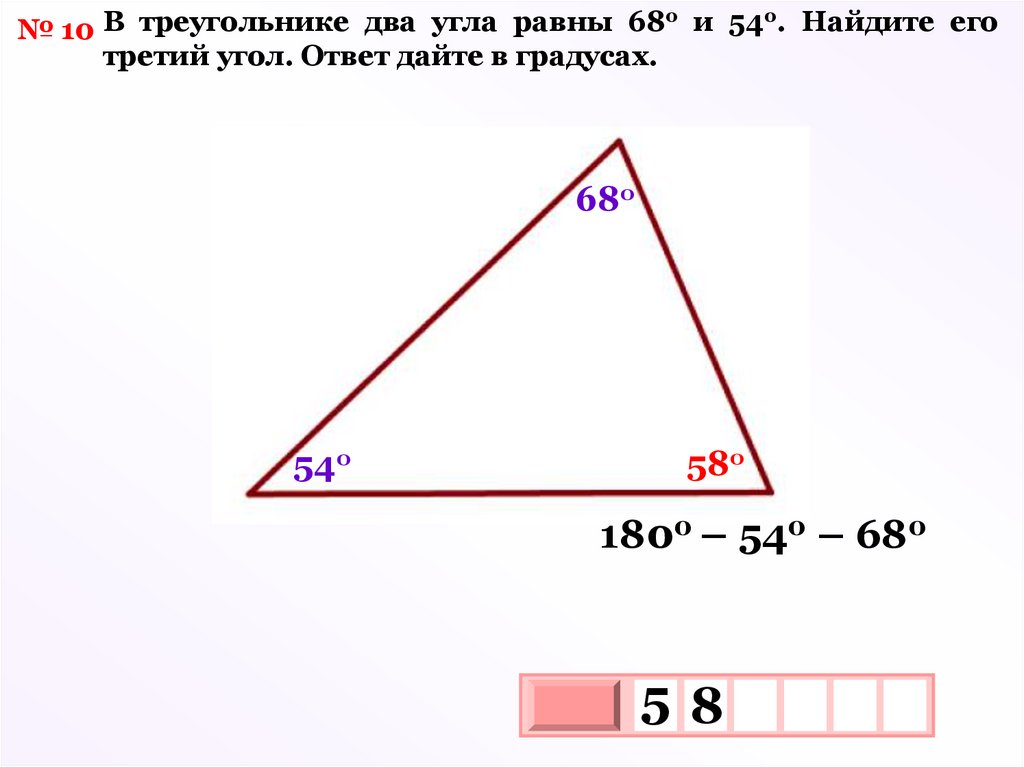
оо
№ 10 В треугольнике два угла равны 68 и 54 . Найдите его
третий угол. Ответ дайте в градусах.
68о
54о
58о
1800 – 540 – 680
58
3
10 х
х
28.
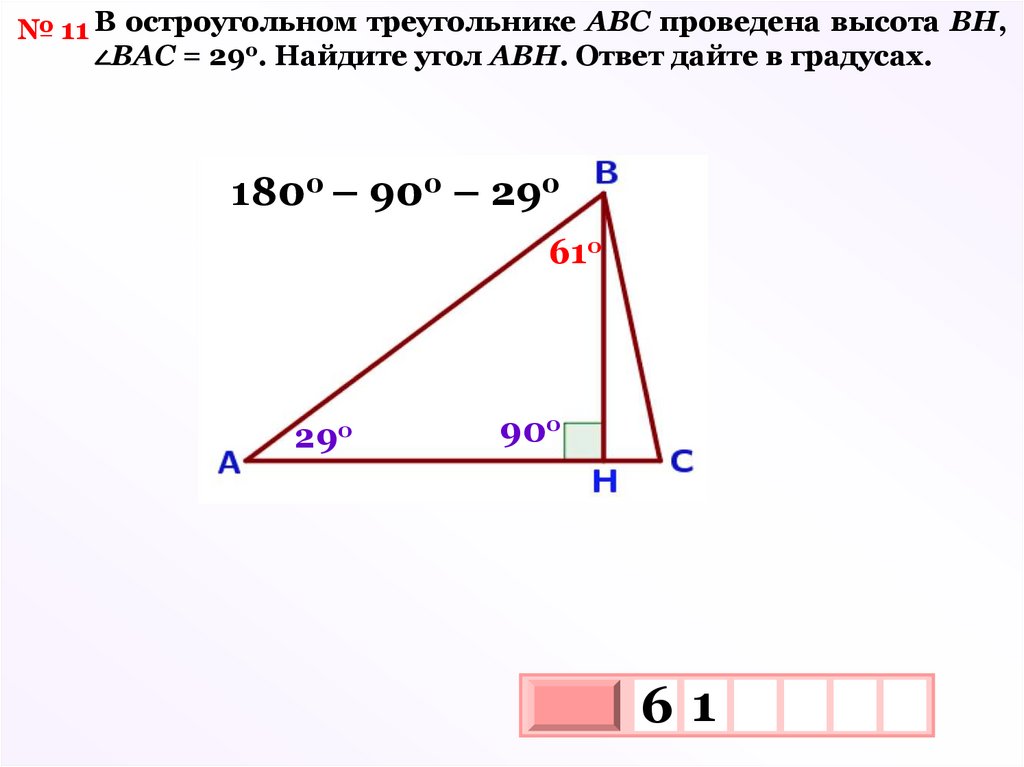
№ 11 В остроугольном треугольнике АВС проведена высота ВН,∠ВАС = 29о. Найдите угол АВН. Ответ дайте в градусах.
1800 – 900 – 290
61о
29о
90о
61
3
10 х
х
29.
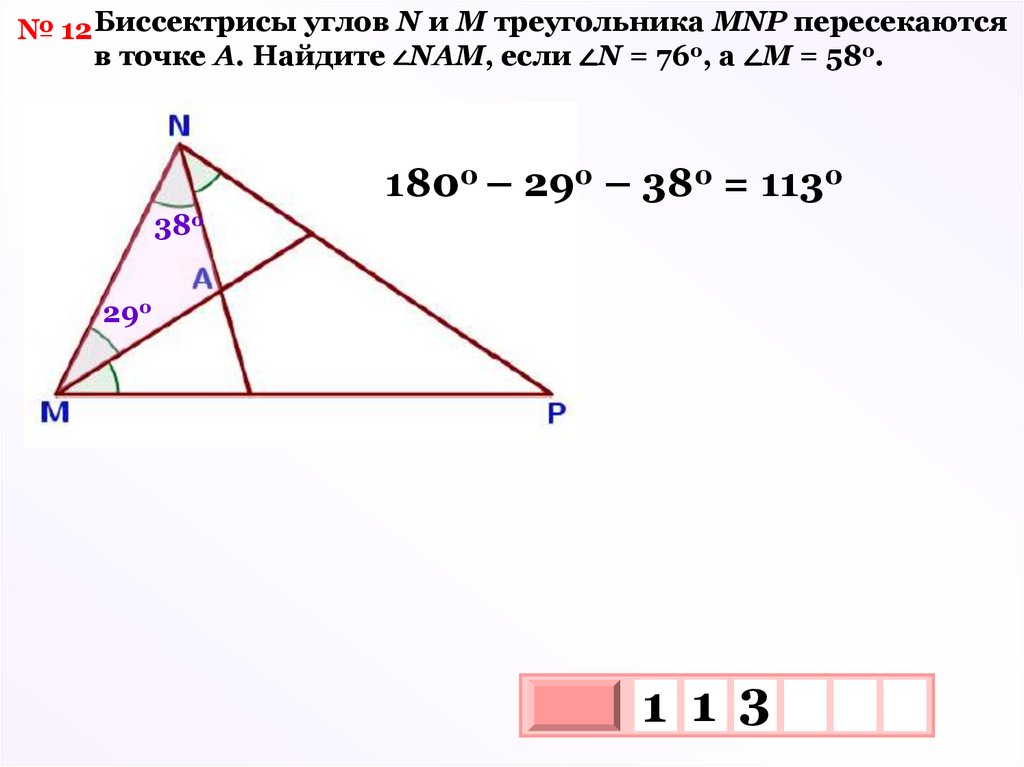
№ 12 Биссектрисы углов N и M треугольника МNР пересекаютсяв точке А. Найдите ∠NАМ, если ∠N = 76о, а ∠М = 58о.
1800 – 290 – 380 = 1130
38о
29о
1 1 3
3
10 х
х
30.
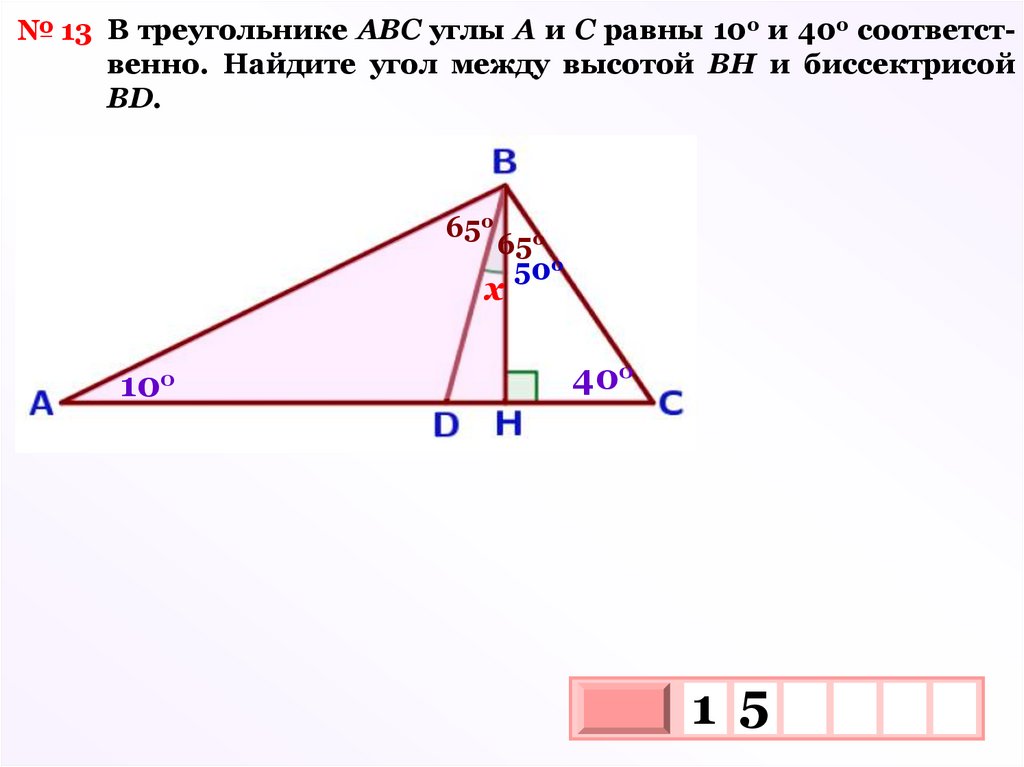
№ 13 В треугольнике АВС углы A и C равны 10о и 40о соответственно. Найдите угол между высотой ВН и биссектрисойВD.
65о
65о
50о
х
10о
40о
1 5
3
10 х
х
31.
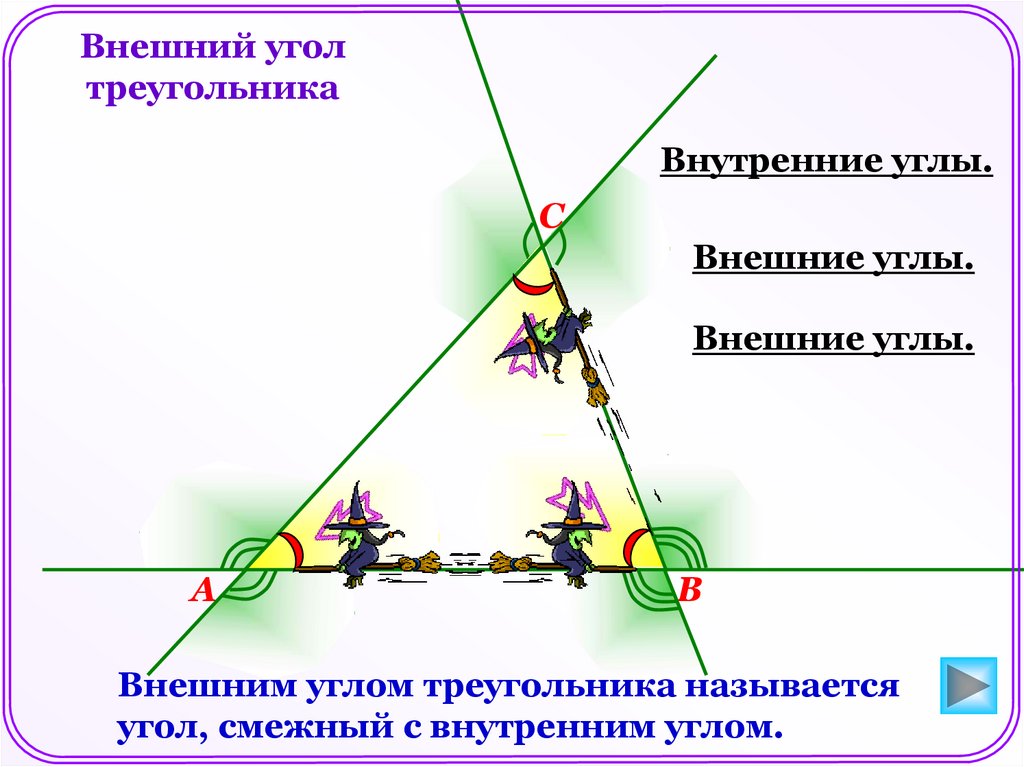
Внешний уголтреугольника
Внутренние углы.
С
Внешние углы.
Внешние углы.
А
В
Внешним углом треугольника называется
угол, смежный с внутренним углом.
32.
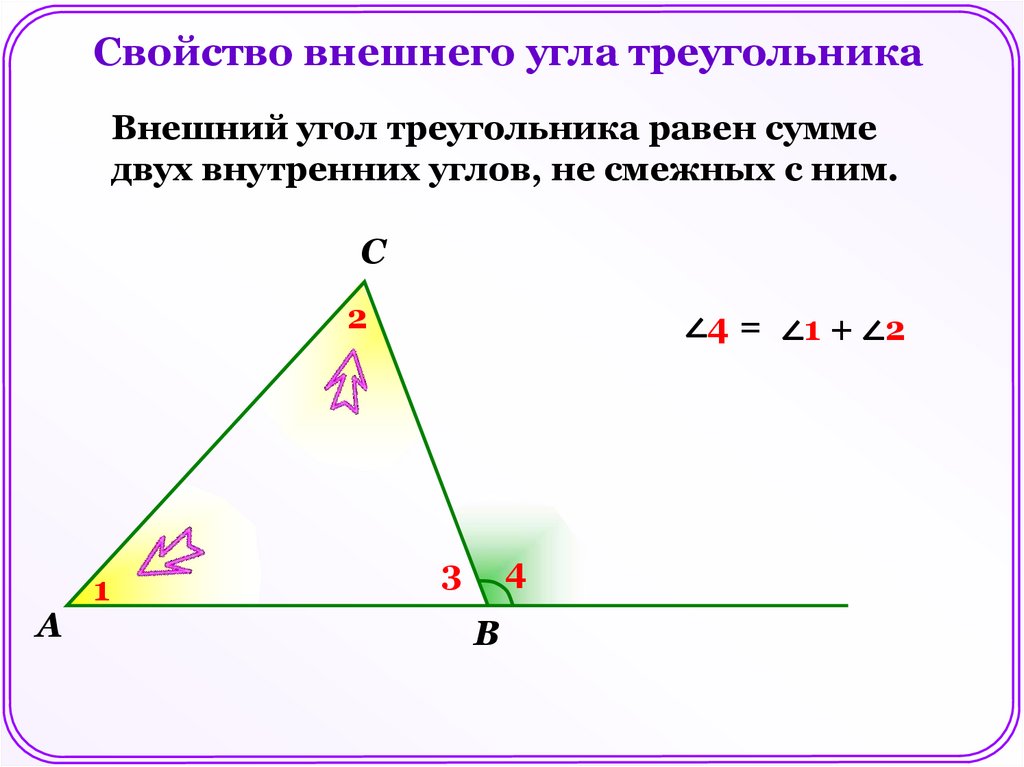
Свойство внешнего угла треугольникаВнешний угол треугольника равен сумме
двух внутренних углов, не смежных с ним.
С
2
А
1
∠4 = ∠1 + ∠2
4
3
В
33.
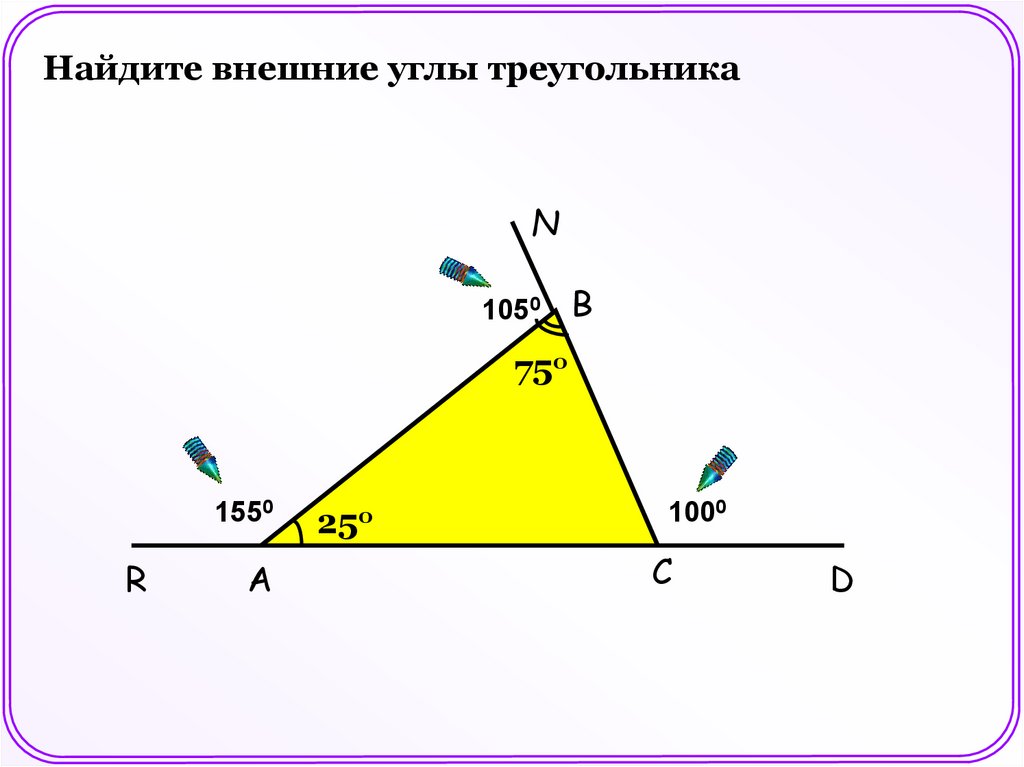
Найдите внешние углы треугольникаN
1050
В
75о
1550
R
А
25о
1000
С
D
34.
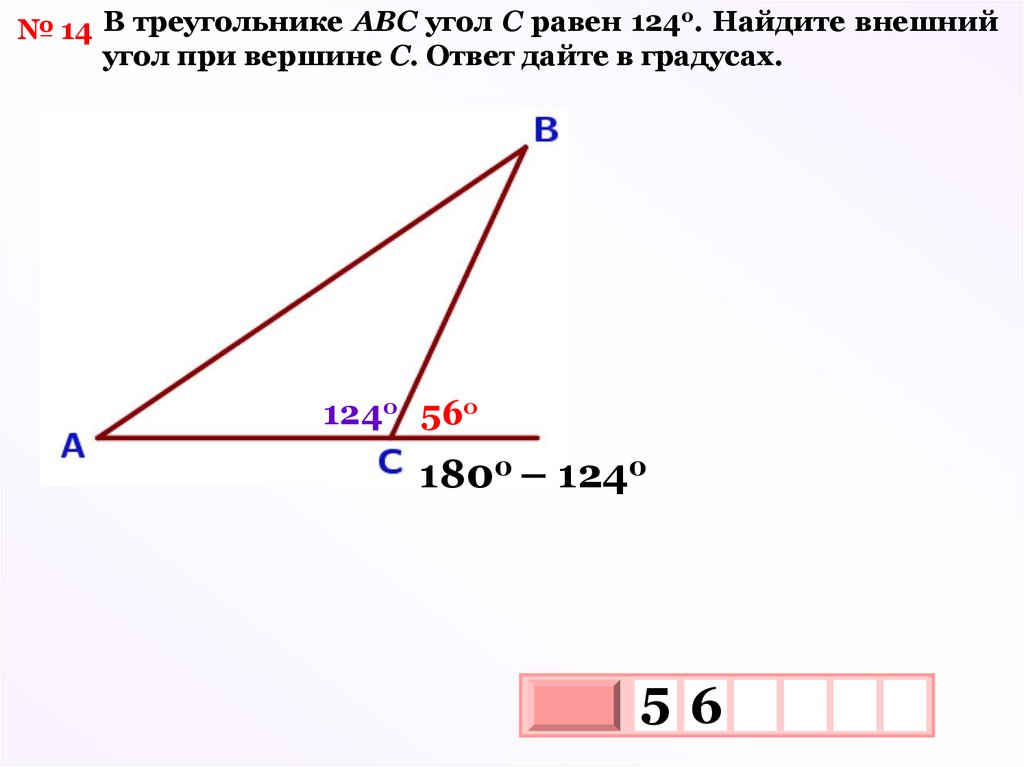
№ 14 В треугольнике АВС угол С равен 124 . Найдите внешнийугол при вершине С. Ответ дайте в градусах.
о
124о 56о
1800 – 1240
56
3
10 х
х
35.
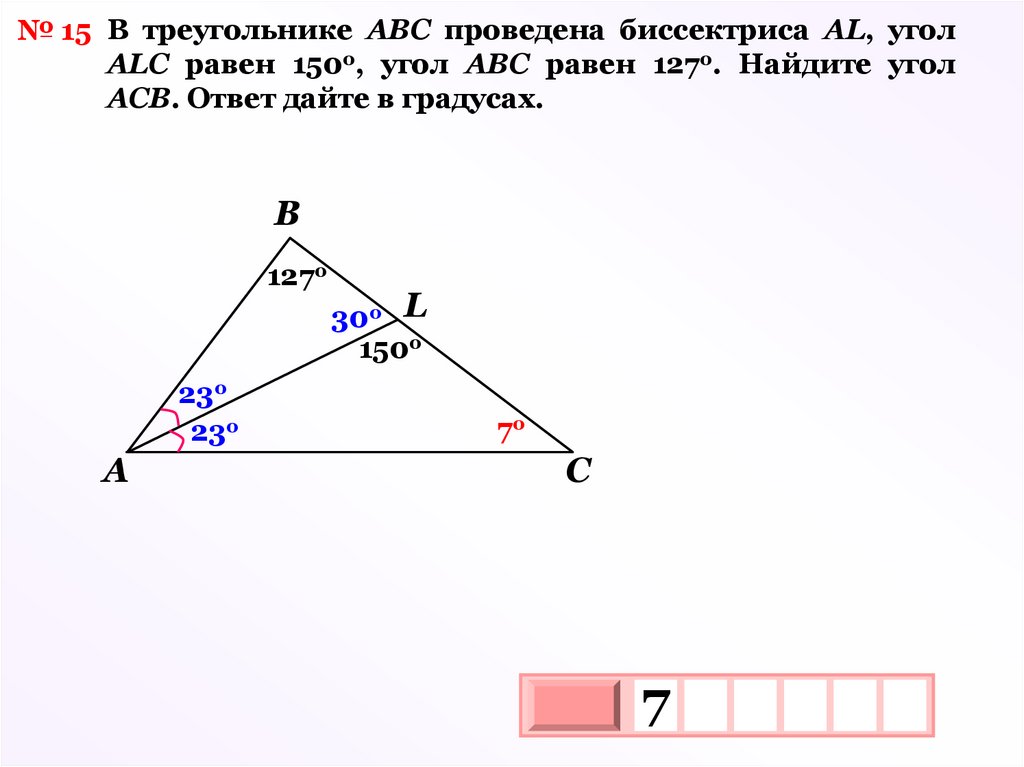
№ 15 В треугольнике АВС проведена биссектриса AL, уголALC равен 150о, угол АВС равен 127о. Найдите угол
АСВ. Ответ дайте в градусах.
B
127о
23о
23о
A
30о L
150о
7о
C
7
3
10 х
х
36.
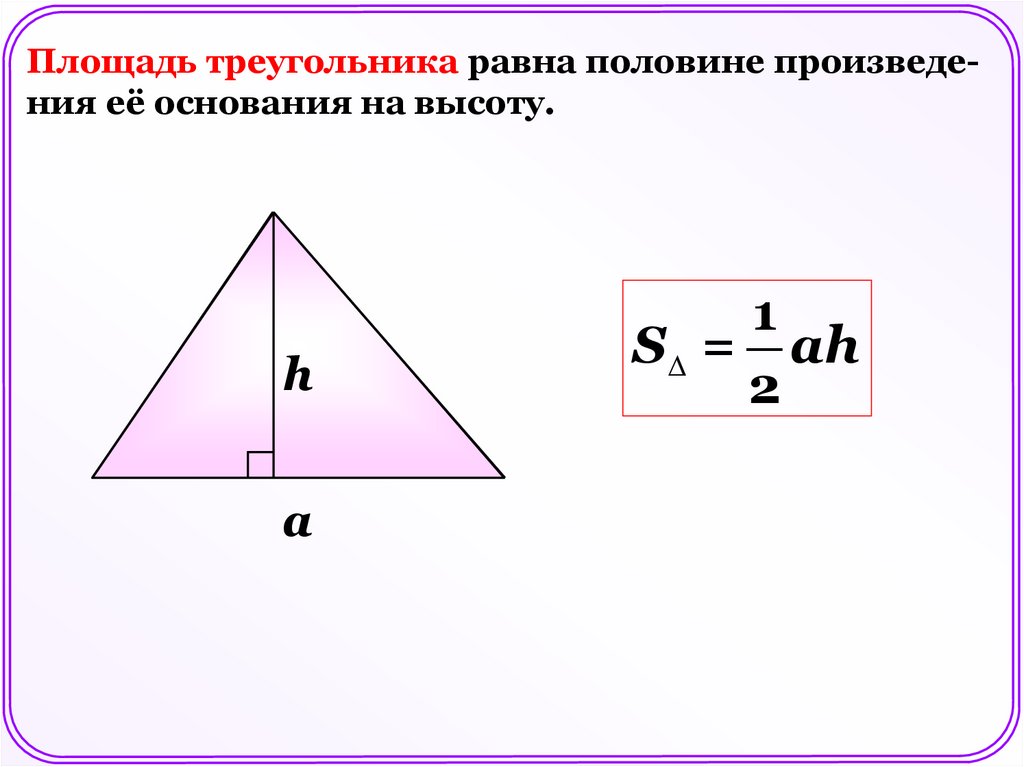
Площадь треугольника равна половине произведения её основания на высоту.h
а
1
S = ah
2
37.
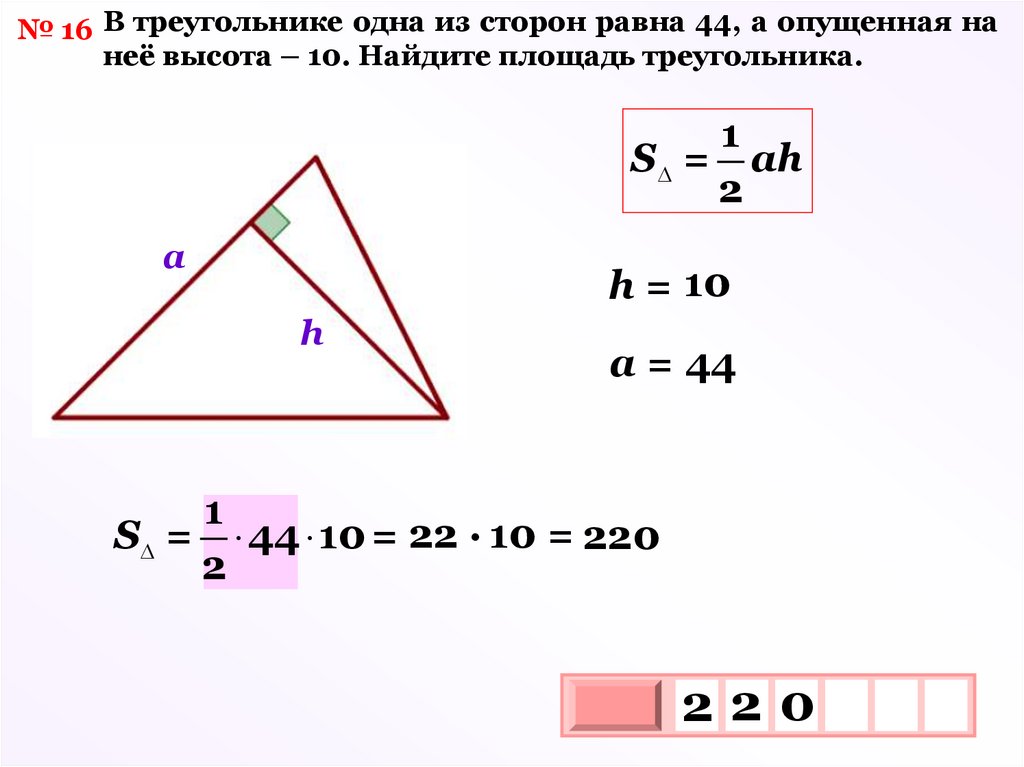
№ 16 В треугольнике одна из сторон равна 44, а опущенная нанеё высота – 10. Найдите площадь треугольника.
1
S = ah
2
а
h = 10
h
а = 44
1
S = 44 10 = 22 · 10 = 220
2
220
3
10 х
х
38.
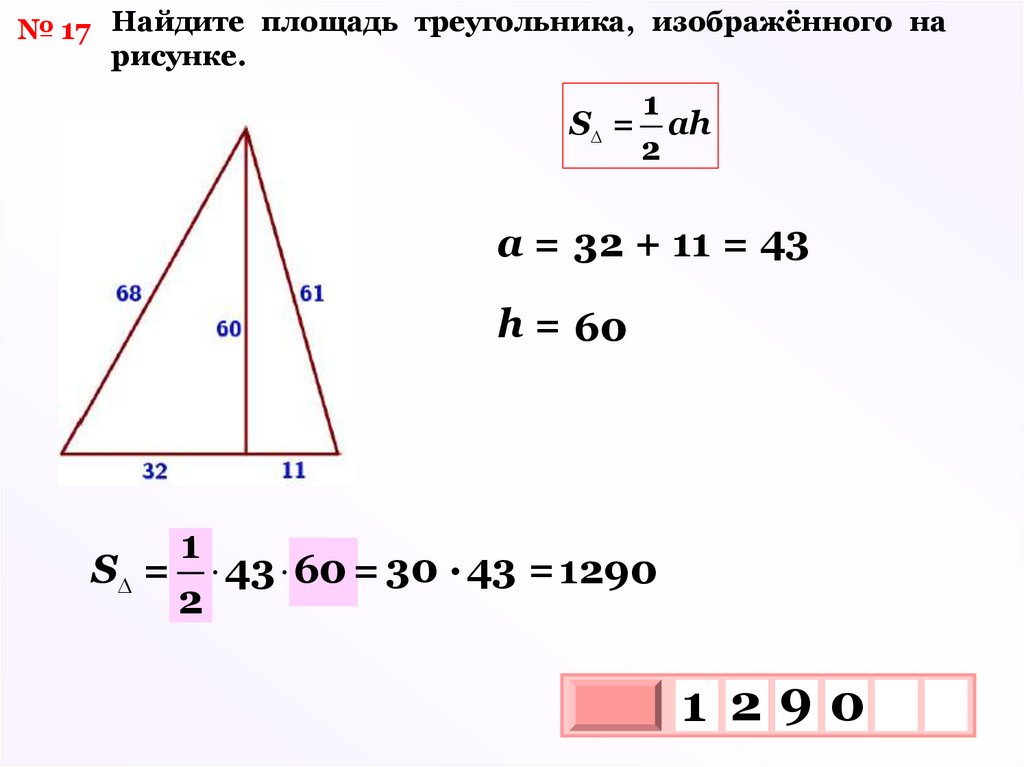
№ 17 Найдите площадь треугольника, изображённого нарисунке.
S =
1
ah
2
а = 32 + 11 = 43
h = 60
1
S = 43 60 = 30 · 43 = 1290
2
1 290
3
10 х
х
39.
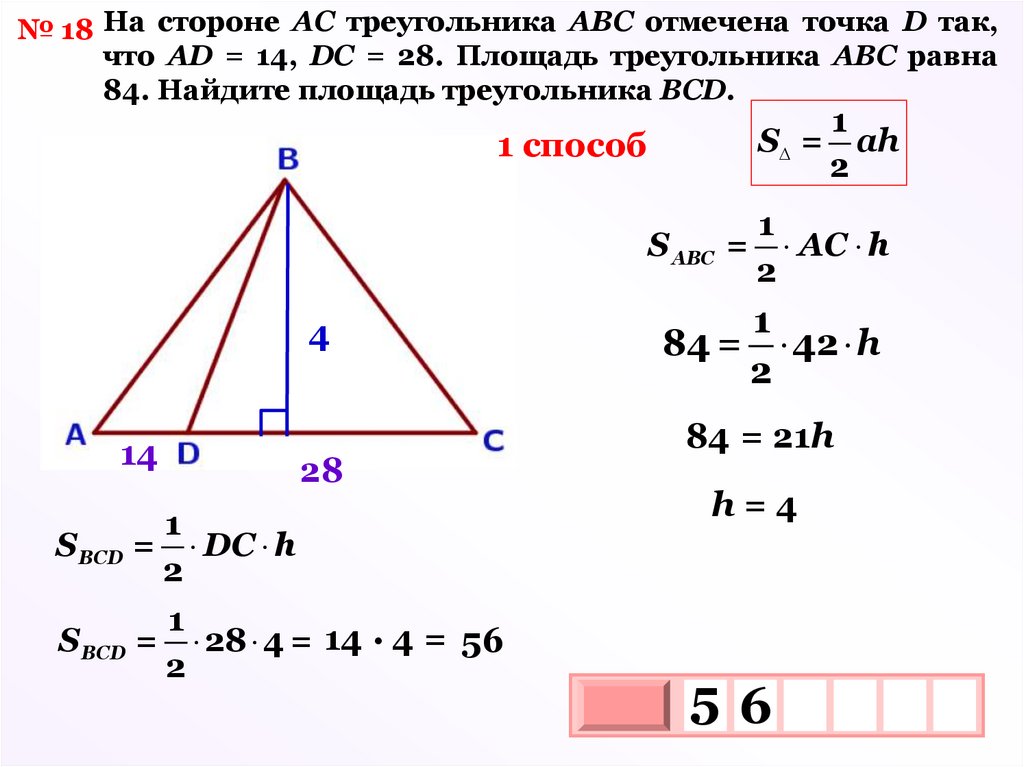
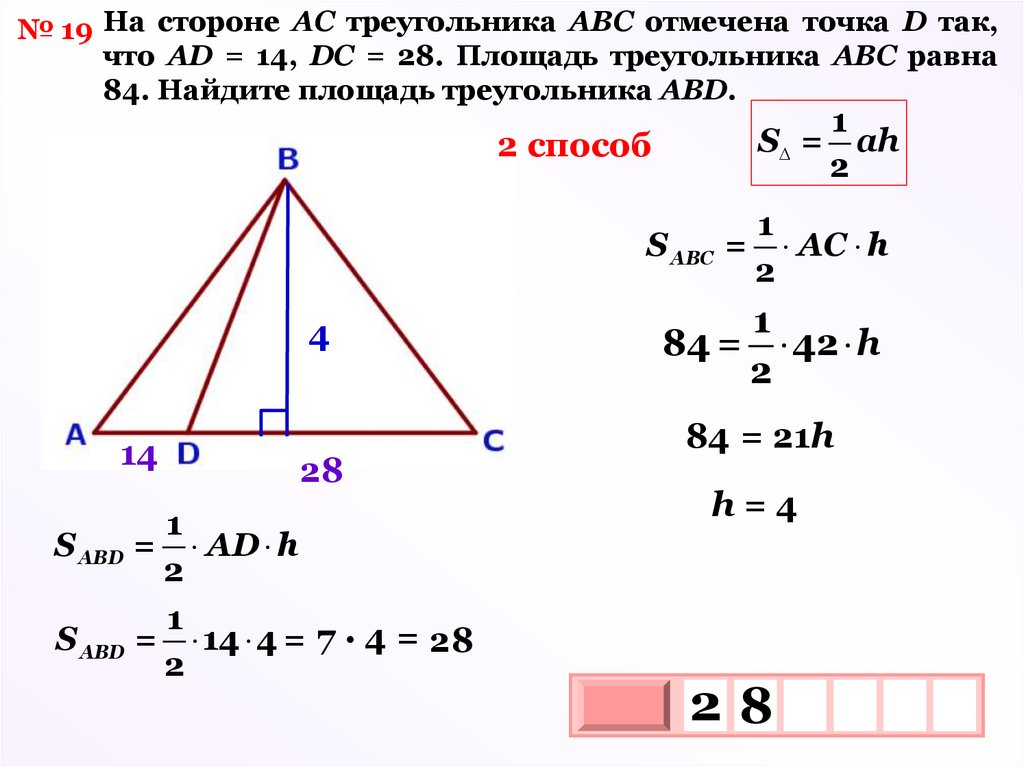
№ 18 На стороне АС треугольника АВС отмечена точка D так,что АD = 14, DC = 28. Площадь треугольника АВС равна
84. Найдите площадь треугольника ВСD.
1 способ
S =
1
ah
2
1
S АВС = АC h
2
h4
14
28
1
DC h
2
1
S ВСD = 28 4 = 14 · 4 = 56
2
1
84 = 42 h
2
84 = 21h
h=4
S ВСD =
56
3
10 х
х
40.
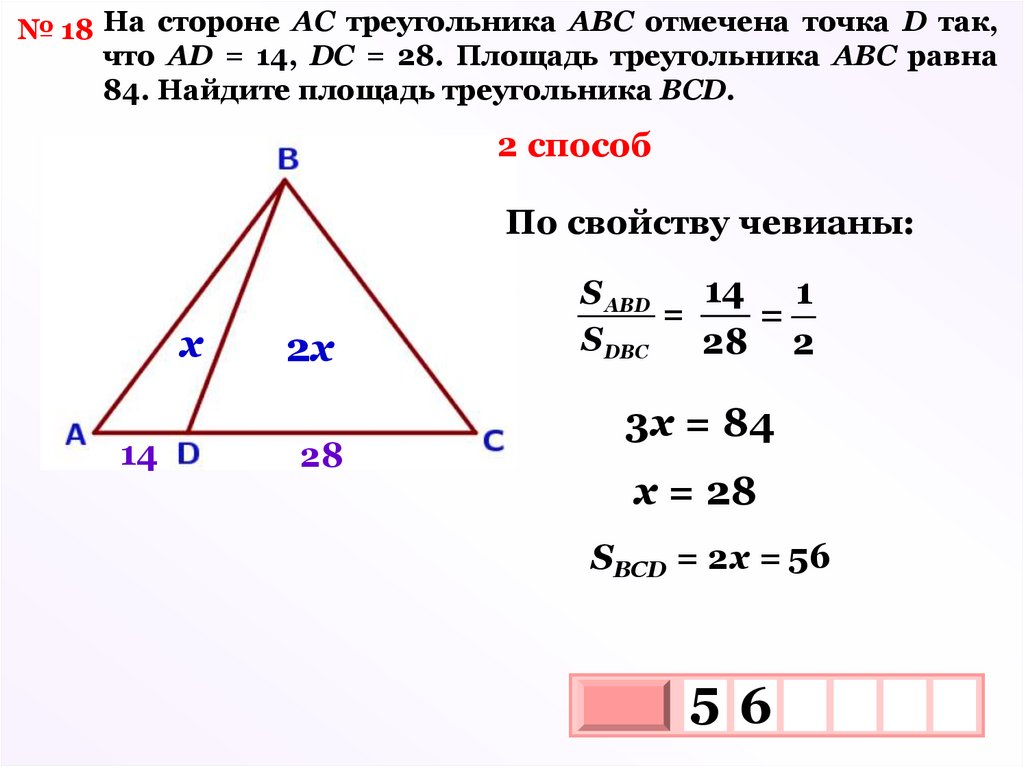
№ 18 На стороне АС треугольника АВС отмечена точка D так,что АD = 14, DC = 28. Площадь треугольника АВС равна
84. Найдите площадь треугольника ВСD.
2 способ
По свойству чевианы:
х
14
2х
28
14 1
S АВD
=
=
S DВС
28 2
3х = 84
х = 28
SBCD = 2х = 56
56
3
10 х
х
41.
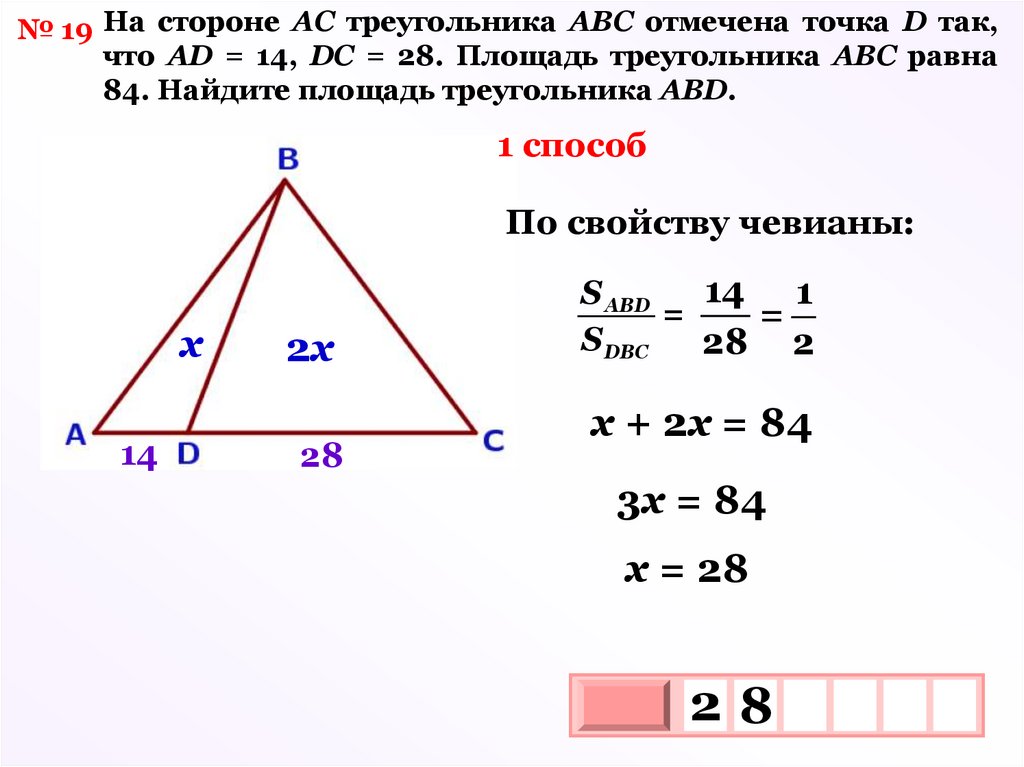
№ 19 На стороне АС треугольника АВС отмечена точка D так,что АD = 14, DC = 28. Площадь треугольника АВС равна
84. Найдите площадь треугольника АВD.
1 способ
По свойству чевианы:
х
14
2х
28
14 1
S АВD
=
=
S DВС
28 2
х + 2х = 84
3х = 84
х = 28
28
3
10 х
х
42.
№ 19 На стороне АС треугольника АВС отмечена точка D так,что АD = 14, DC = 28. Площадь треугольника АВС равна
84. Найдите площадь треугольника АВD.
2 способ
S =
1
ah
2
1
S АВС = АC h
2
h4
14
28
1
АD h
2
1
S АВD = 14 4 = 7 · 4 = 28
2
1
84 = 42 h
2
84 = 21h
h=4
S АВD =
28
3
10 х
х
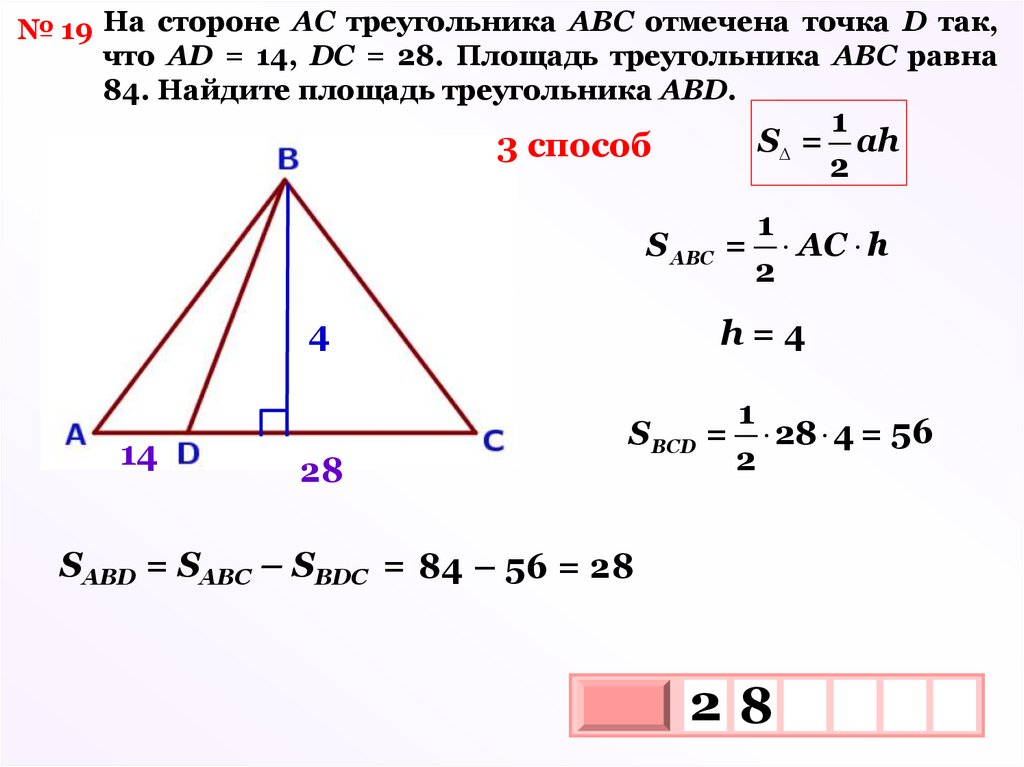
43.
№ 19 На стороне АС треугольника АВС отмечена точка D так,что АD = 14, DC = 28. Площадь треугольника АВС равна
84. Найдите площадь треугольника АВD.
3 способ
S =
1
ah
2
1
S АВС = АC h
2
14
h4
h=4
28
1
S ВСD = 28 4 = 56
2
SABD = SABC – SBDC = 84 – 56 = 28
28
3
10 х
х
44.
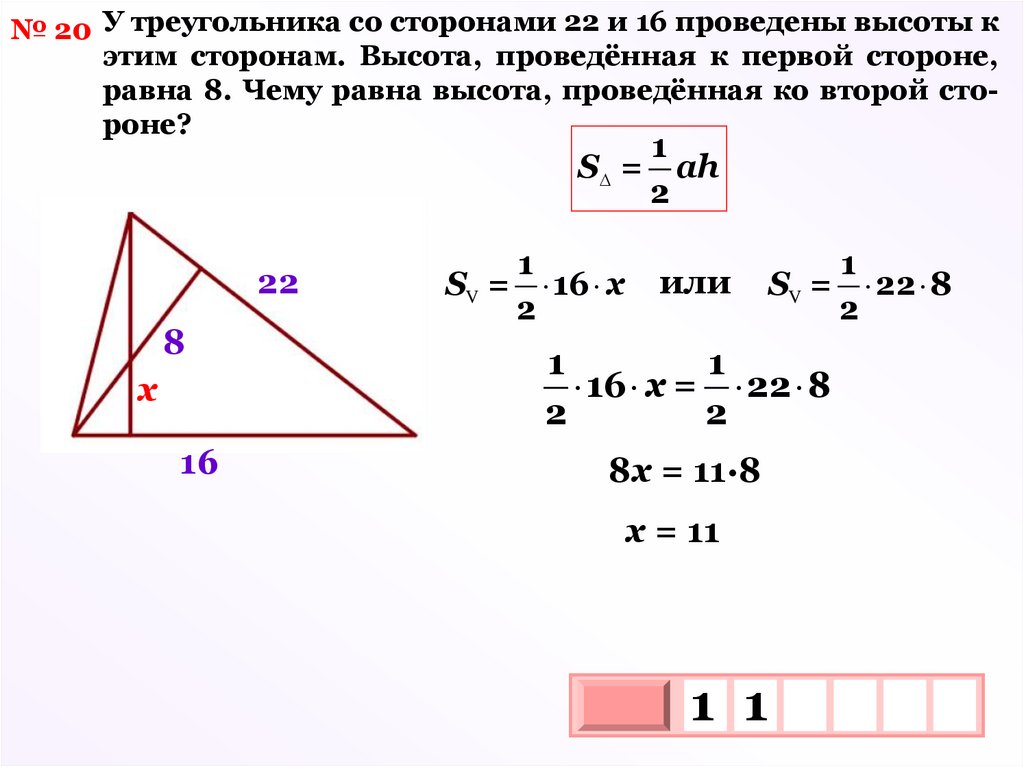
№ 20 У треугольника со сторонами 22 и 16 проведены высоты кэтим сторонам. Высота, проведённая к первой стороне,
равна 8. Чему равна высота, проведённая ко второй стороне?
1
S = ah
2
22
8
х
16
SV =
1
16 х
2
или
SV =
1
22 8
2
1
1
16 х = 22 8
2
2
8х = 11·8
х = 11
1 1
3
10 х
х
45.
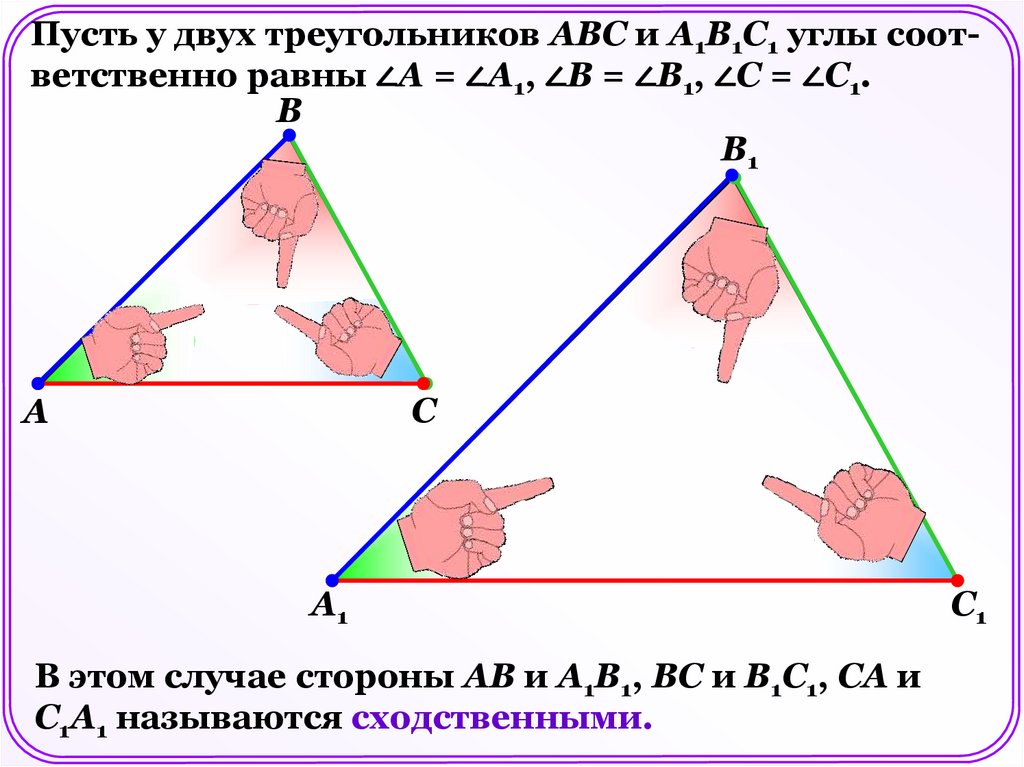
Пусть у двух треугольников АВС и А1В1С1 углы соответственно равны ∠А = ∠А1, ∠В = ∠В1, ∠С = ∠С1.В
В1
С
А
А1
В этом случае стороны АВ и А1В1, ВС и В1С1, СА и
С1А1 называются сходственными.
С1
46.
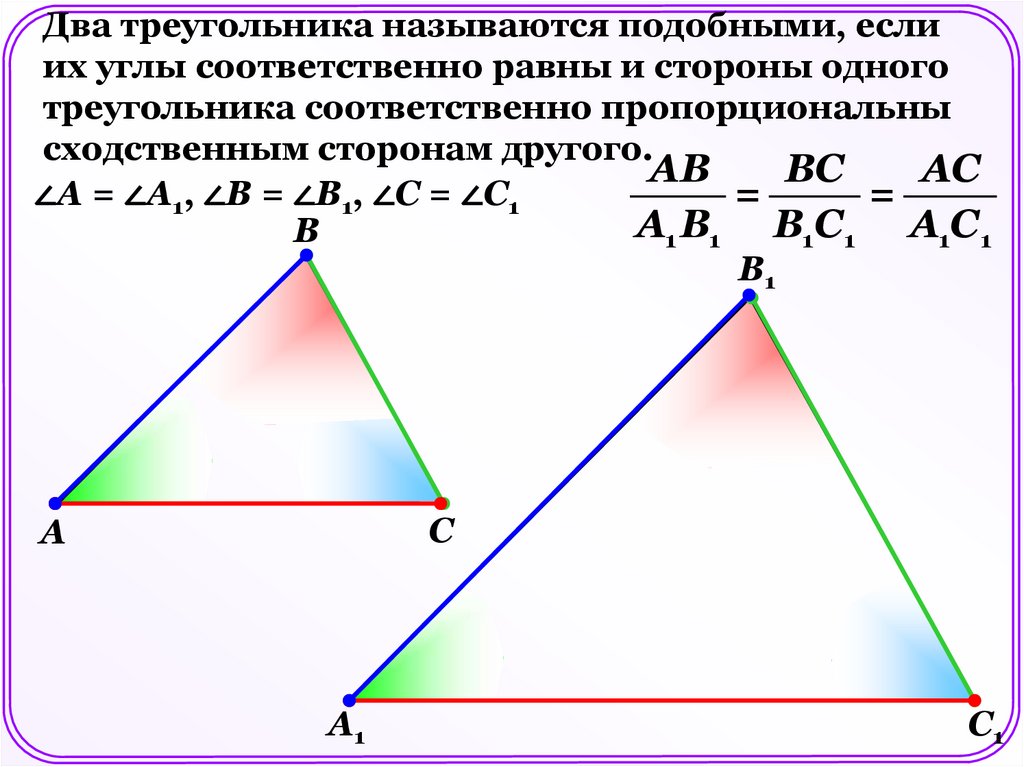
Два треугольника называются подобными, еслиих углы соответственно равны и стороны одного
треугольника соответственно пропорциональны
сходственным сторонам другого.
АВ
ВС
АС
∠А = ∠А1, ∠В = ∠В1, ∠С = ∠С1
=
=
А1 В1 В1С1 А1С1
В
В1
С
А
А1
С1
47.
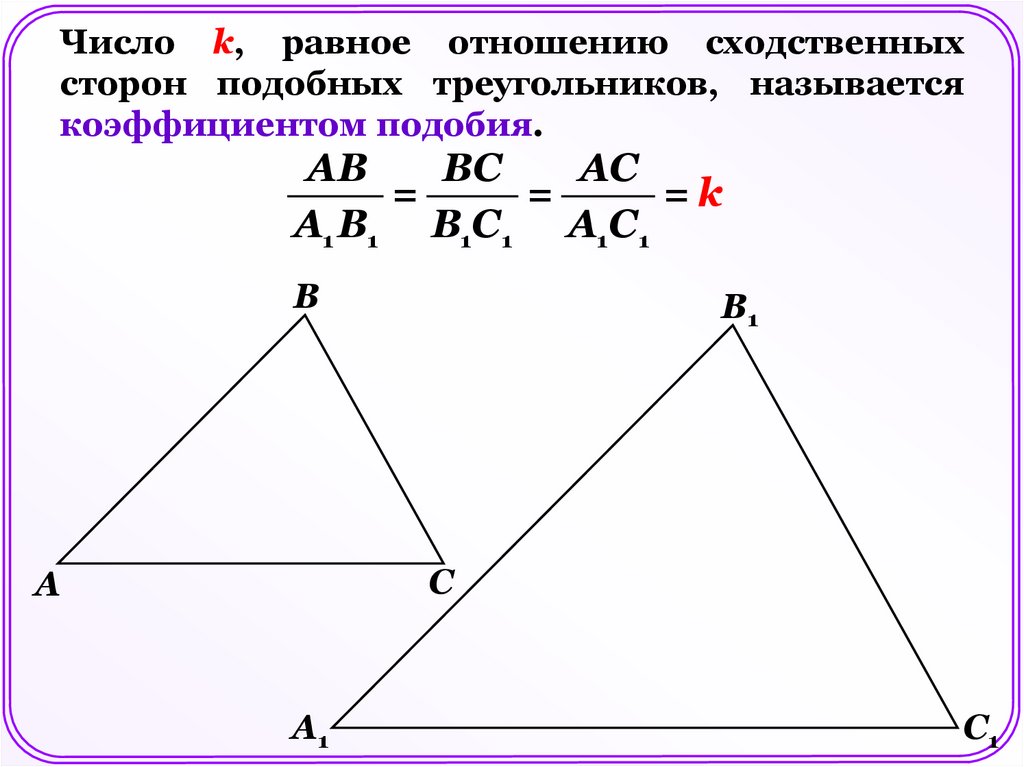
Число k, равное отношению сходственныхсторон подобных треугольников, называется
коэффициентом подобия.
АВ
ВС
АС
=
=
=k
А1 В1 В1С1 А1С1
В
В1
С
А
А1
С1
48.
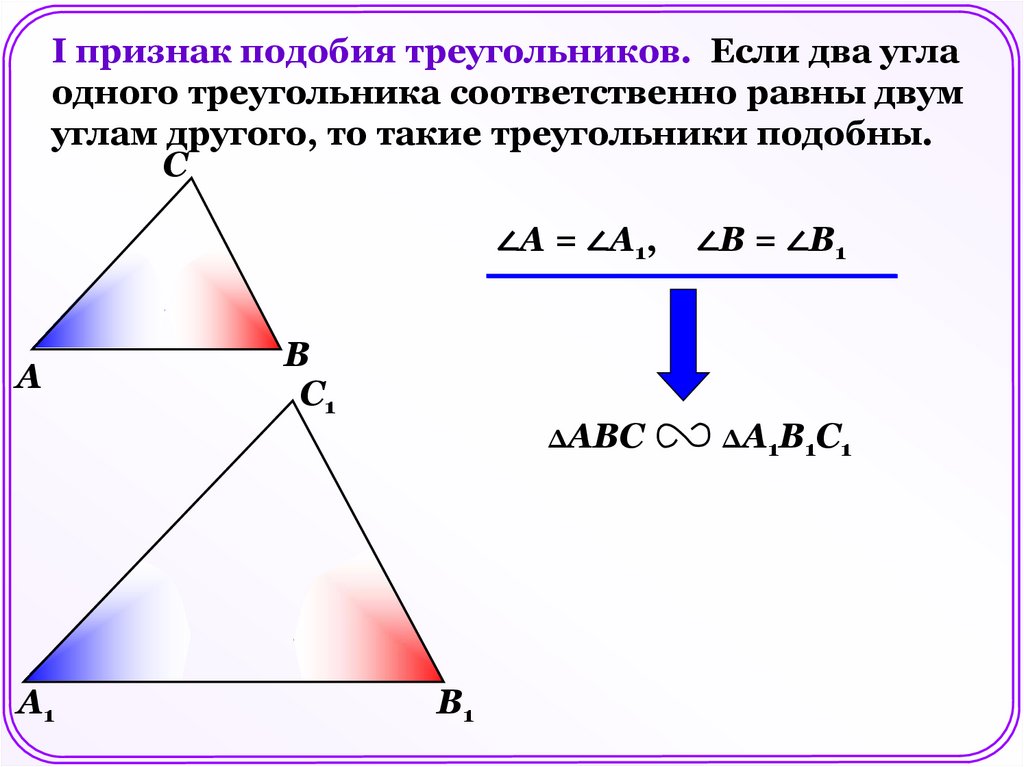
I признак подобия треугольников. Если два углаодного треугольника соответственно равны двум
углам другого, то такие треугольники подобны.
С
А
А1
В
С1
В1
∠А = ∠А1,
∠В = ∠В1
ΔАВС
ΔА1В1С1
49.
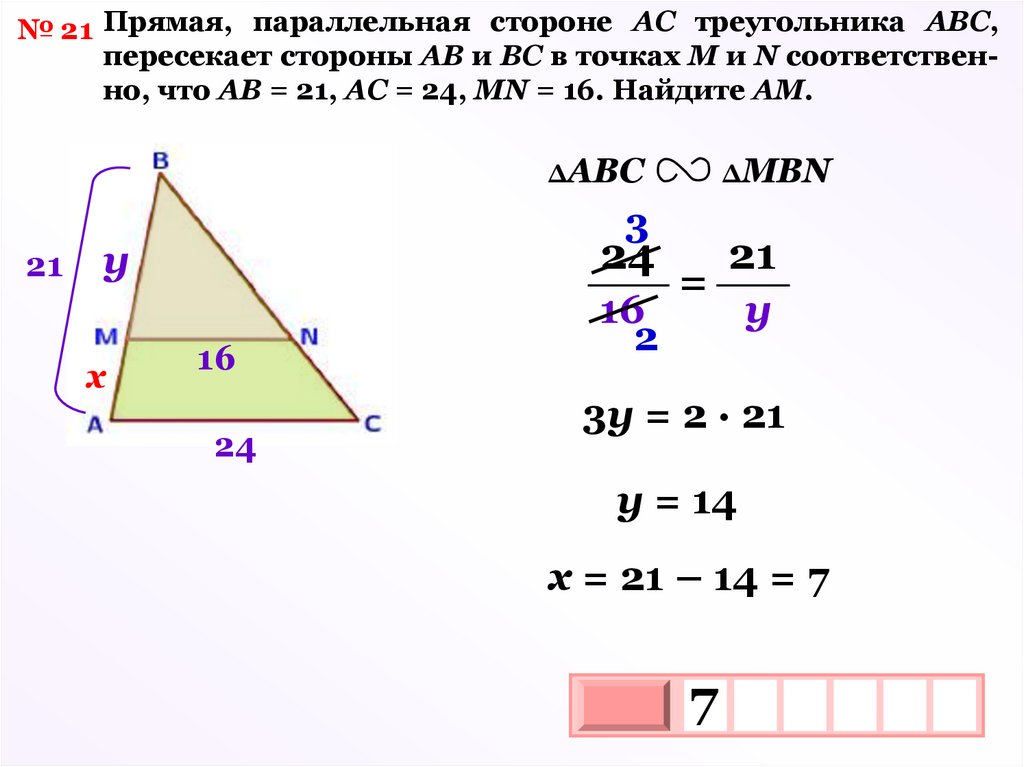
№ 21 Прямая, параллельная стороне АС треугольника АВС,пересекает стороны АВ и ВС в точках М и N соответственно, что АВ = 21, АC = 24, MN = 16. Найдите АМ.
ΔАВС
21
3
24
у
х
ΔМВN
16
24
16
2
=
21
у
3у = 2 · 21
у = 14
х = 21 – 14 = 7
7
3
10 х
х
50.
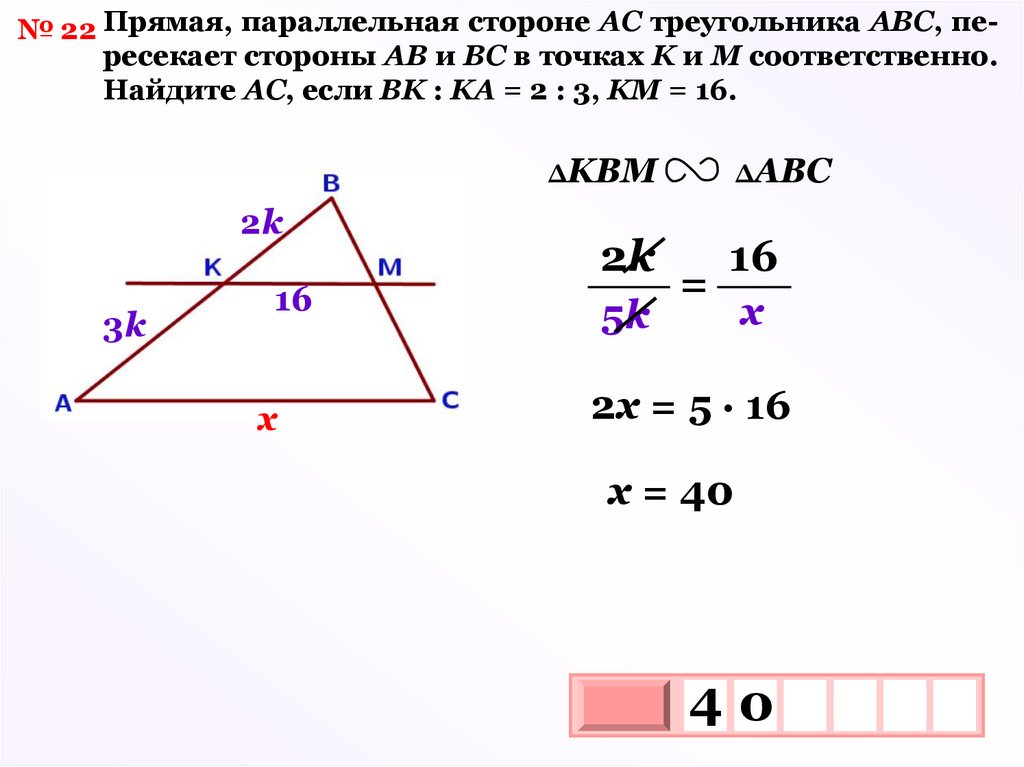
№ 22 Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках K и М соответственно.Найдите АС, если ВK : KА = 2 : 3, KМ = 16.
ΔKBM
2k
3k
16
х
2k
5k
ΔABC
=
16
х
2х = 5 · 16
х = 40
40
3
10 х
х
51.
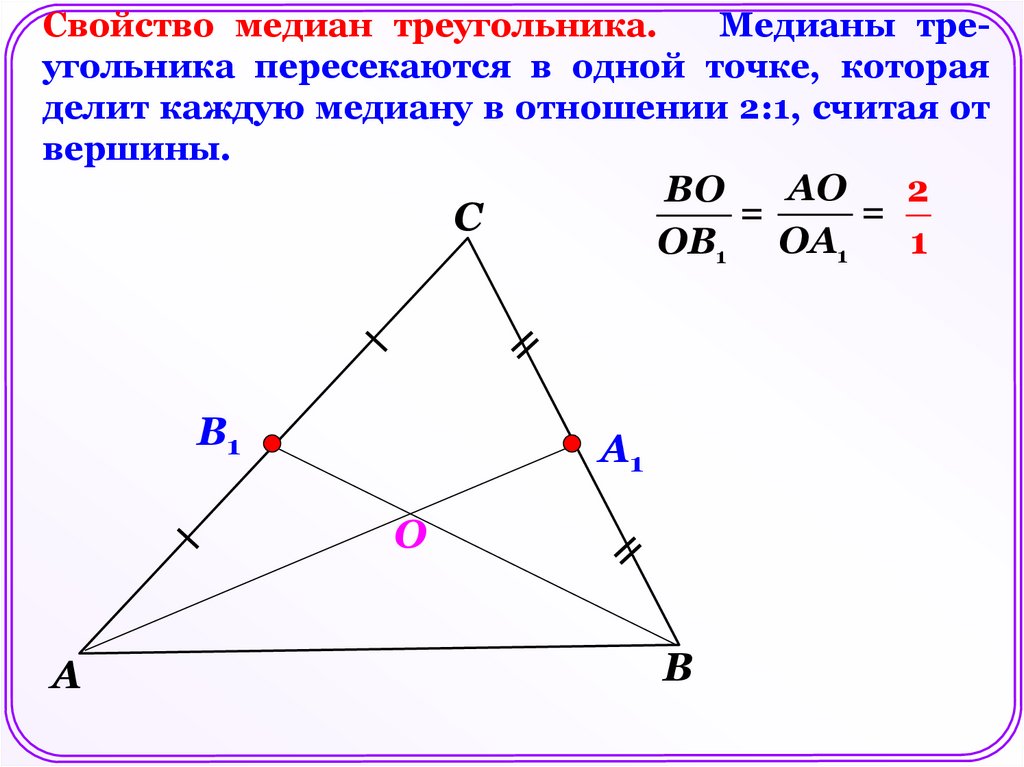
Свойство медиан треугольника.Медианы треугольника пересекаются в одной точке, которая
делит каждую медиану в отношении 2:1, считая от
вершины.
АО
2
ВО
=
=
ОВ1 ОА1
1
С
B1
A1
O
А
В
52.
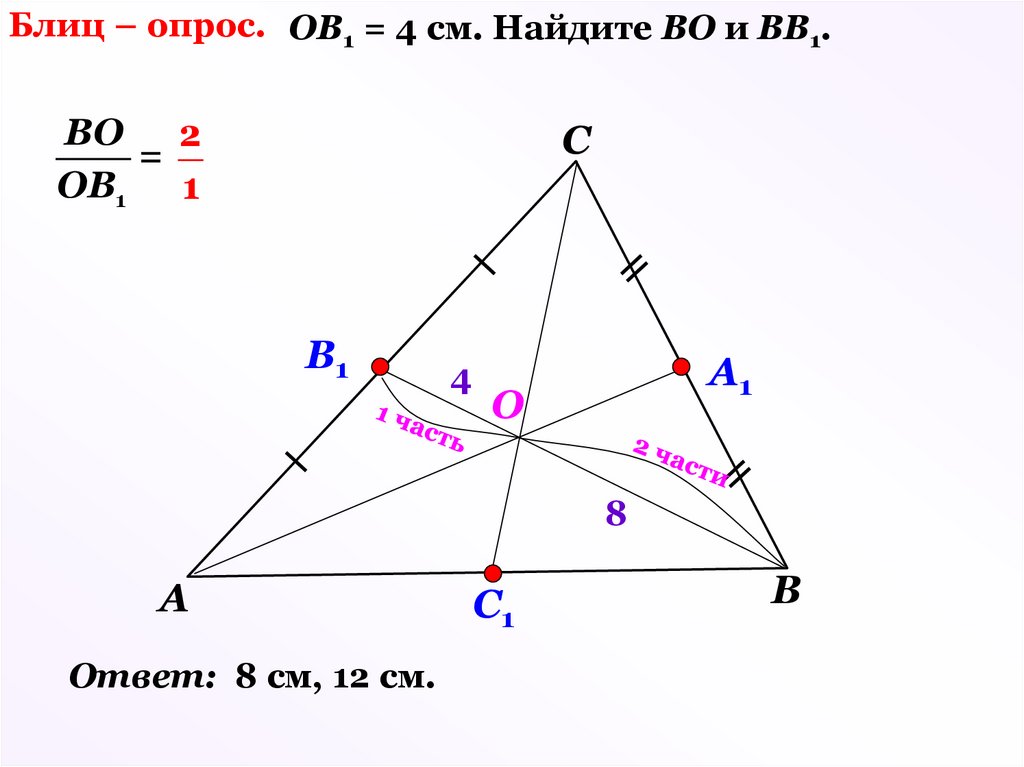
Блиц – опрос. ОВ1 = 4 см. Найдите ВО и ВВ1.ВО 2
=
ОВ1
1
С
B1
4
A1
O
8
А
Ответ: 8 см, 12 см.
C1
В
53.
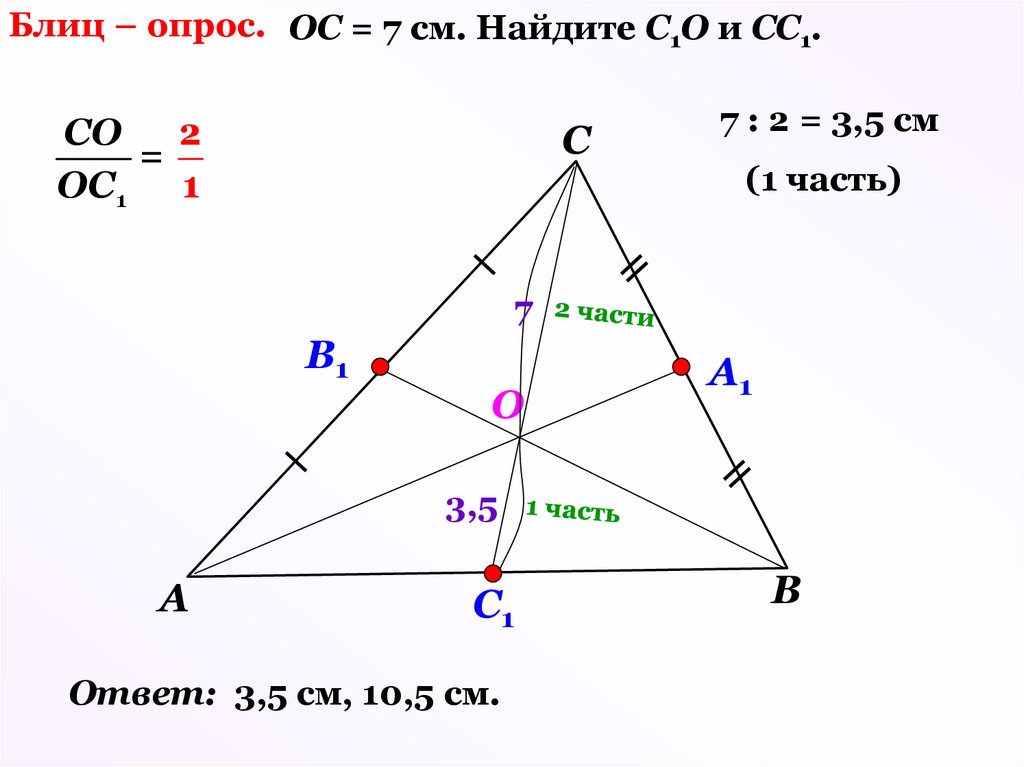
Блиц – опрос. ОС = 7 см. Найдите С1О и СС1.2
СО
=
ОС 1 1
С
7 : 2 = 3,5 см
(1 часть)
7
B1
O
A1
3,5
А
C1
Ответ: 3,5 см, 10,5 см.
В
54.
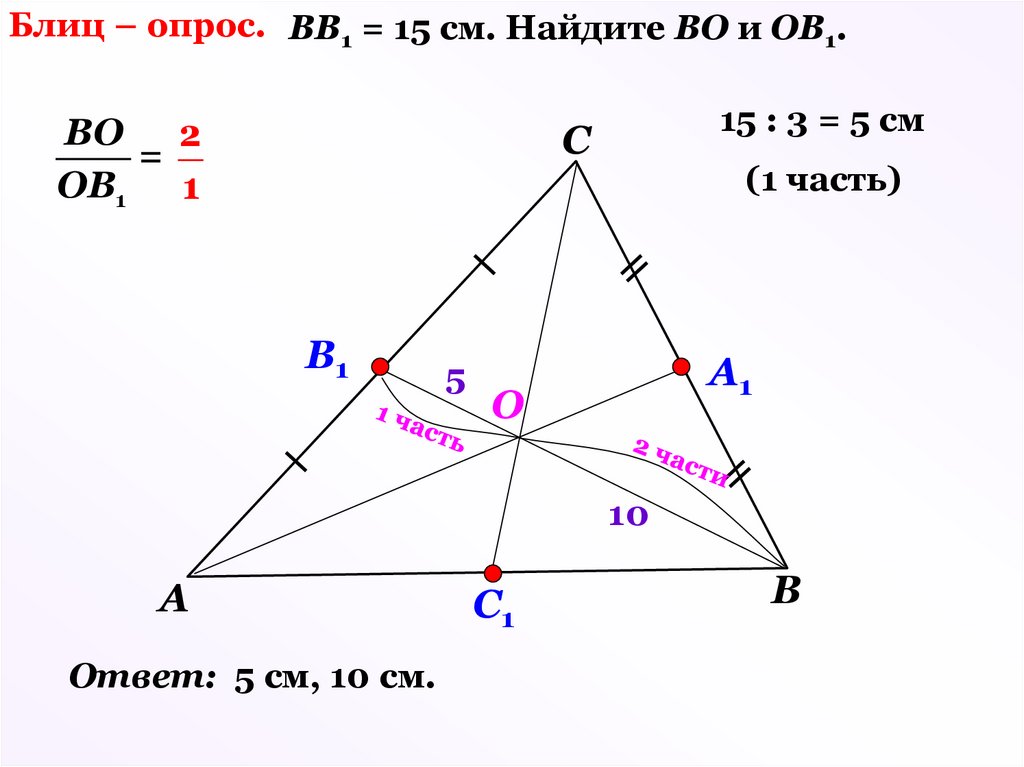
Блиц – опрос. ВВ1 = 15 см. Найдите ВО и ОВ1.ВО 2
=
ОВ1
1
15 : 3 = 5 см
С
B1
5
(1 часть)
A1
O
10
А
Ответ: 5 см, 10 см.
C1
В
55.
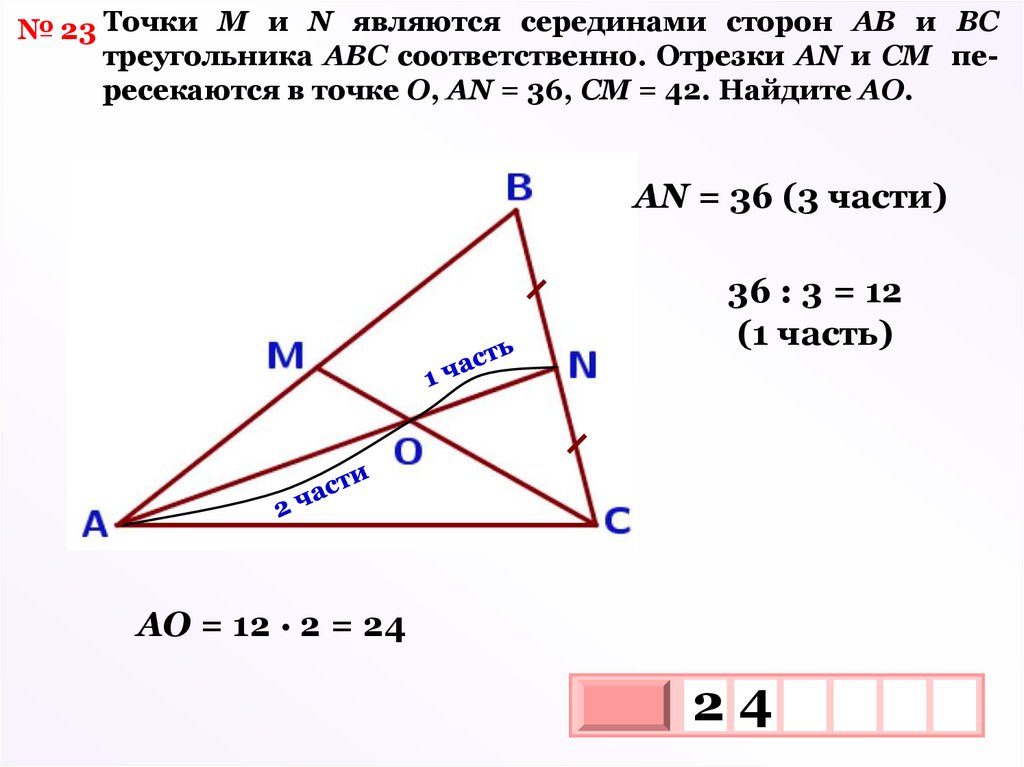
№ 23 Точки М и N являются серединами сторон АВ и ВСтреугольника АВС соответственно. Отрезки АN и СМ пересекаются в точке О, АN = 36, CМ = 42. Найдите АО.
АN = 36 (3 части)
36 : 3 = 12
(1 часть)
АО = 12 · 2 = 24
24
3
10 х
х
56.
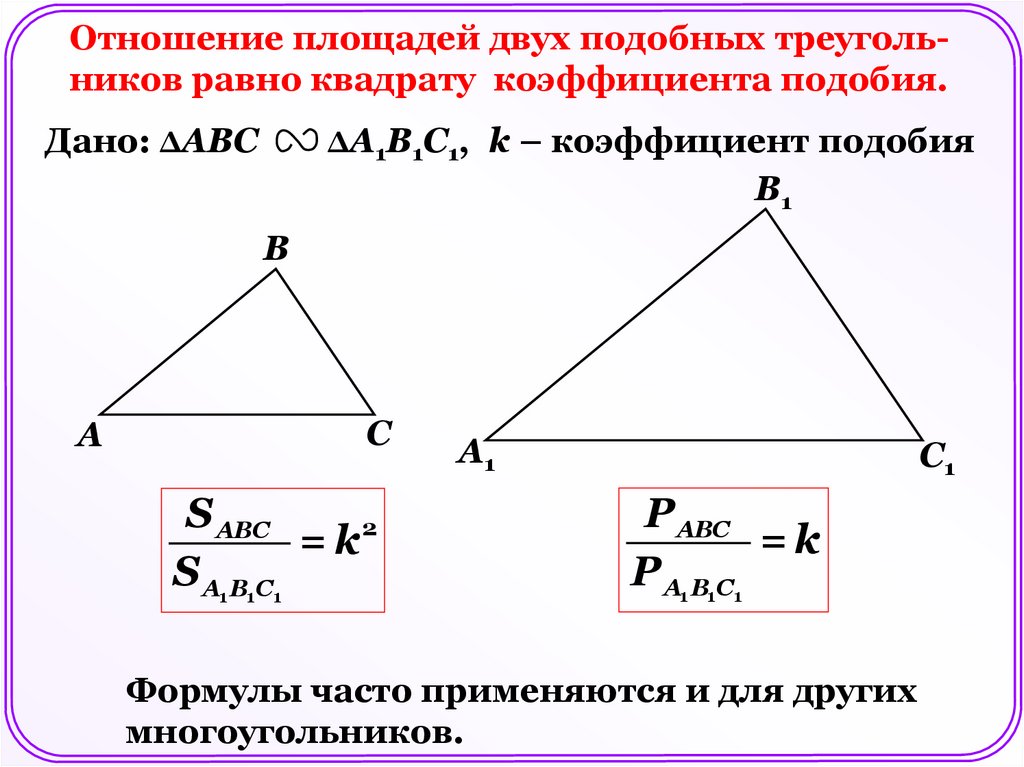
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.Дано: ΔАВС
ΔА1В1С1, k – коэффициент подобия
В1
В
А
С
S АВС
= k2
S А1 В1С1
А1
С1
Р АВС
=k
Р А1 В1С1
Формулы часто применяются и для других
многоугольников.
57.
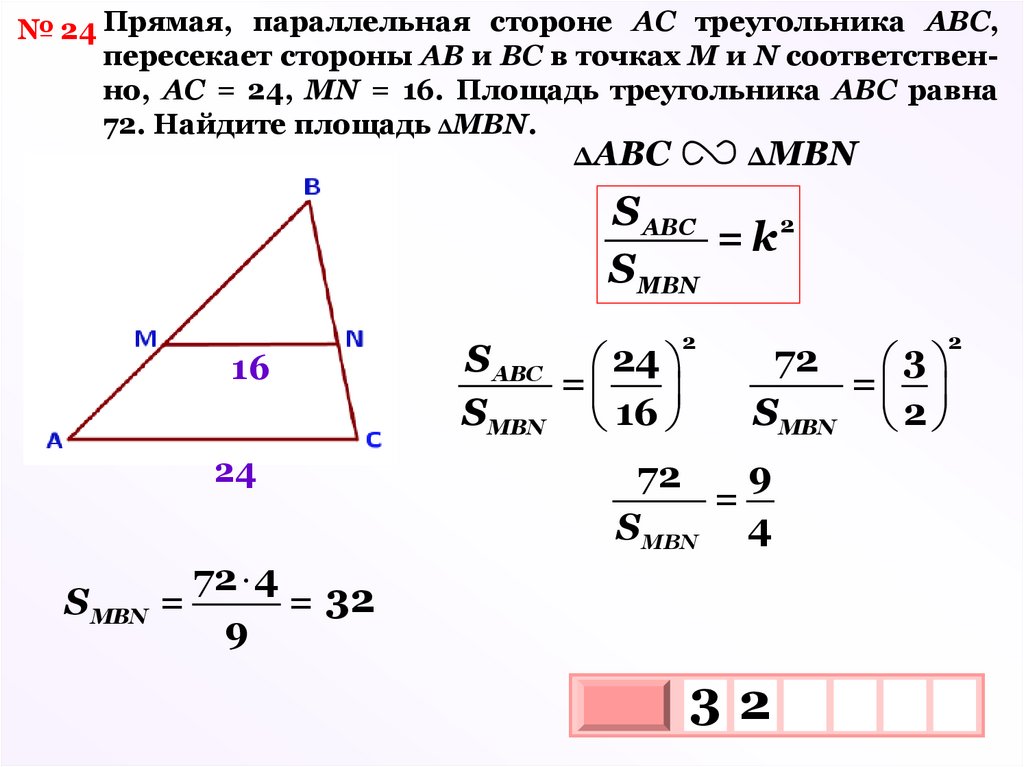
№ 24 Прямая, параллельная стороне АС треугольника АВС,пересекает стороны АВ и ВС в точках М и N соответственно, АС = 24, MN = 16. Площадь треугольника АВС равна
72. Найдите площадь ΔМВN.
ΔАВС
ΔМВN
S АВС
= k2
S МВN
16
24
72 4
SМВN =
= 32
9
S АВС 24
=
SМВN 16
2
72
3
=
SМВN 2
72
9
=
S МВN 4
32
3
10 х
х
2
58.
№ 25В треугольнике АВС, DE – средняя линия.
Площадь треугольника СDE равна 57. Найдите
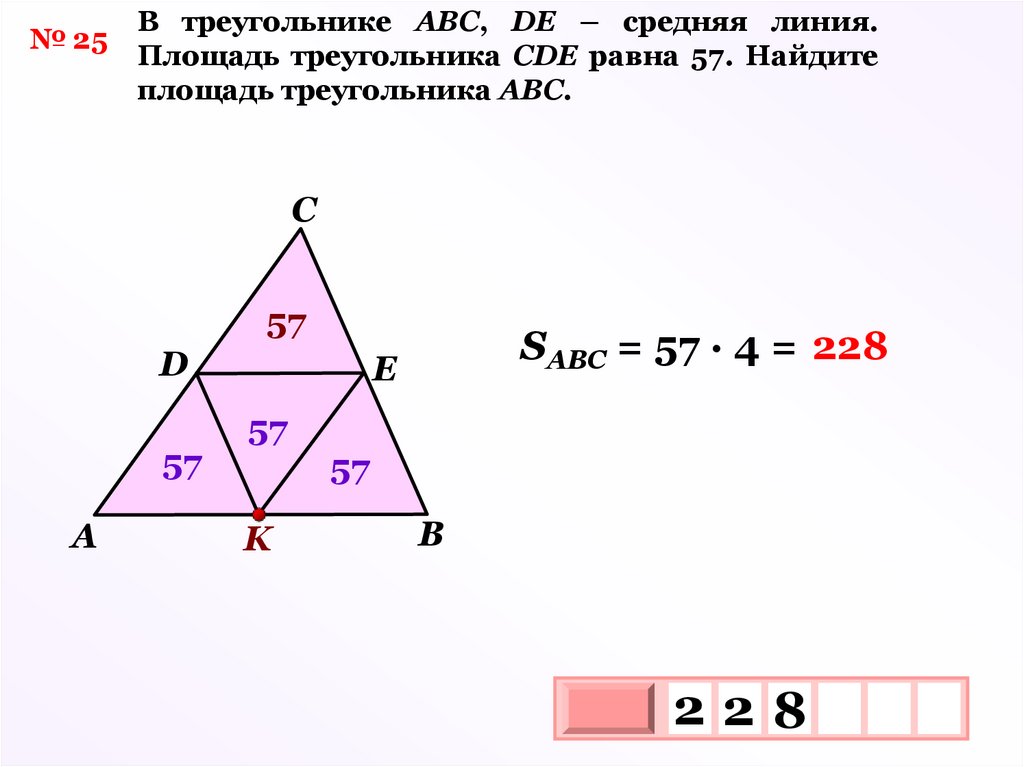
площадь треугольника АВС.
С
57
D
57
А
SАВС = 57 ∙ 4 = 228
Е
57
57
K
В
228
3
10 х
х
59.
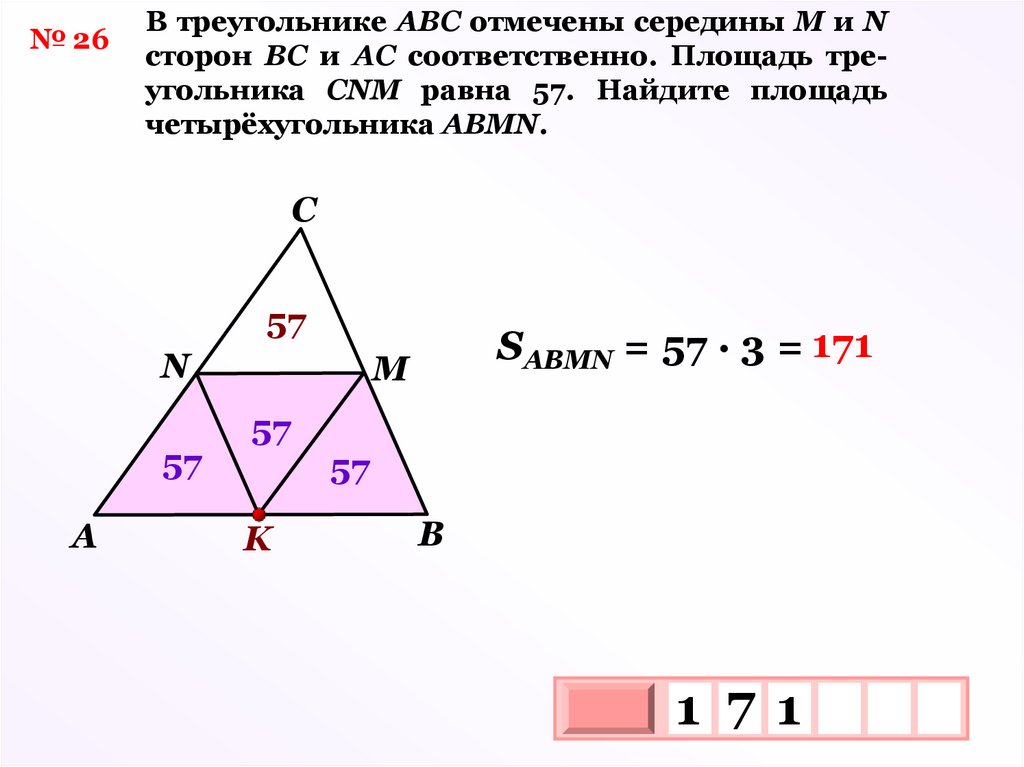
№ 26В треугольнике АВС отмечены середины М и N
сторон ВС и АС соответственно. Площадь треугольника СNM равна 57. Найдите площадь
четырёхугольника АВМN.
С
57
N
57
А
SАВМN = 57 ∙ 3 = 171
М
57
57
K
В
1 7 1
3
10 х
х
60.
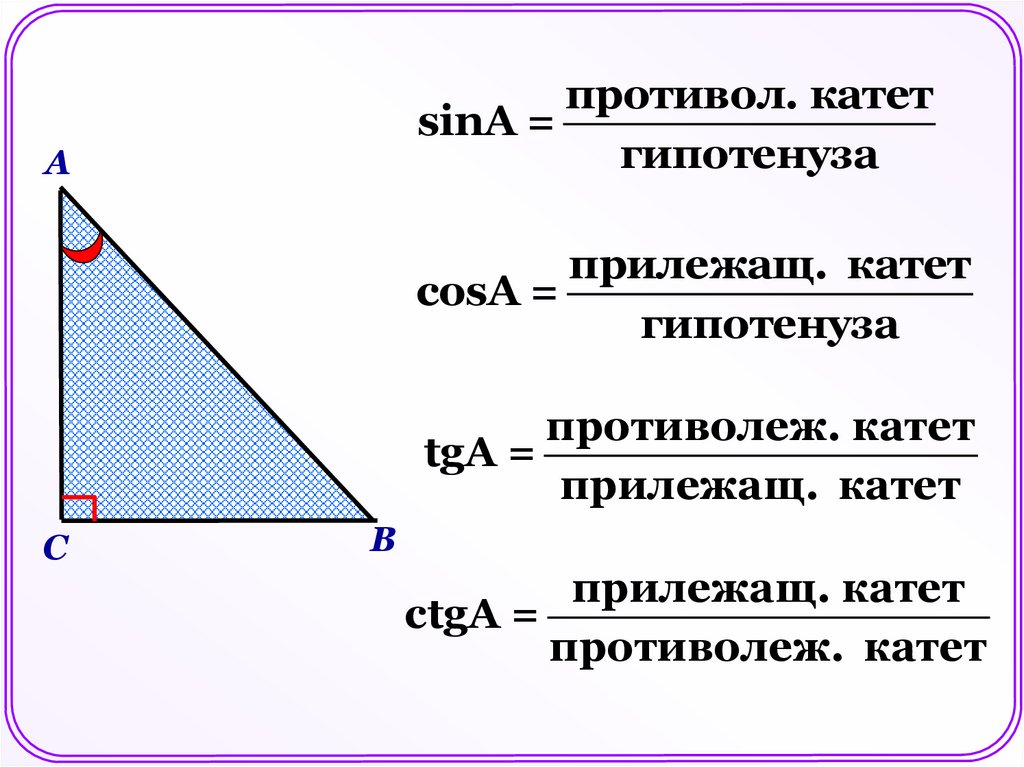
противол. катетsinА =
гипотенуза
А
прилежащ. катет
cosА =
гипотенуза
противолеж. катет
tgА =
прилежащ. катет
С
В
прилежащ. катет
ctgА =
противолеж. катет
61.
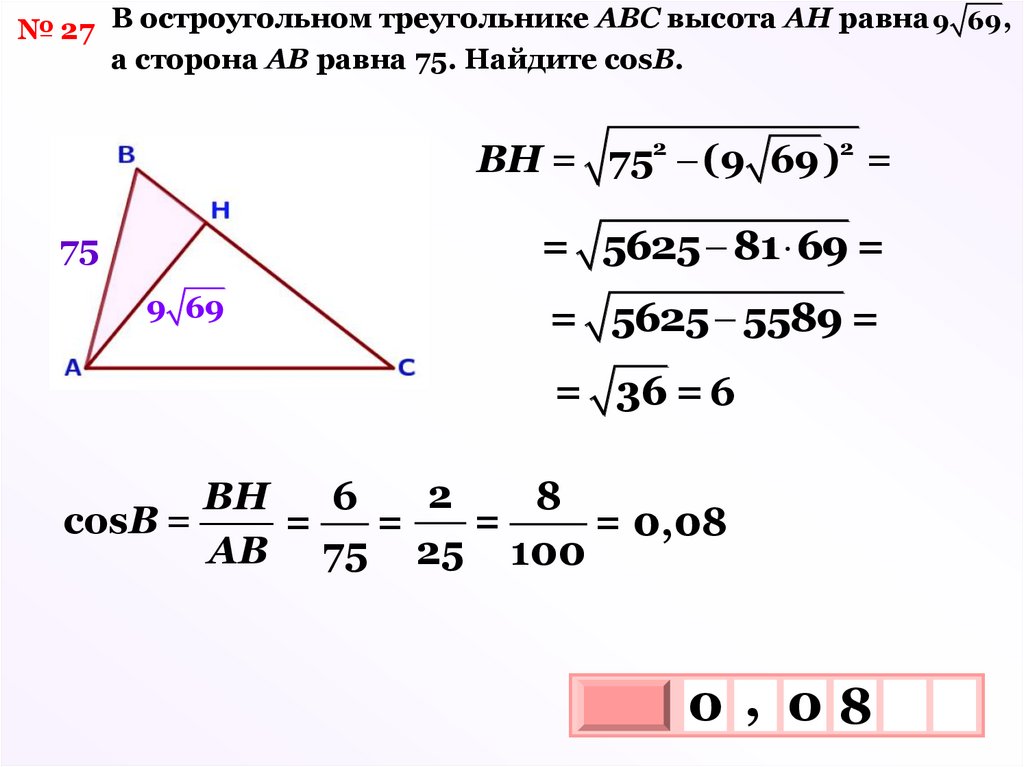
№ 27 В остроугольном треугольнике АВС высота АН равна 9 69,а сторона АВ равна 75. Найдите соsВ.
BН = 752 (9 69)2 =
= 5625 81 69 =
75
9 69
= 5625 5589 =
= 36 = 6
2
6
8
ВН
=
cosВ =
= 0,08
=
=
AB 75 25 100
0 , 08
3
10 х
х
62.
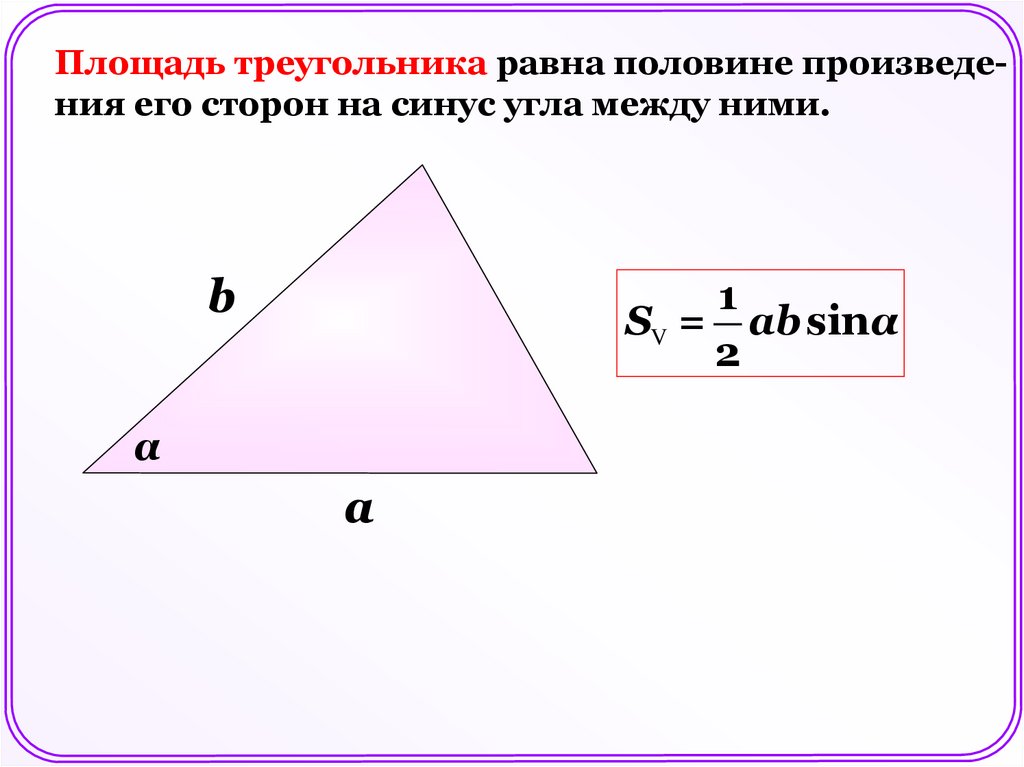
Площадь треугольника равна половине произведения его сторон на синус угла между ними.b
1
SV = аb sinα
2
α
а
63.
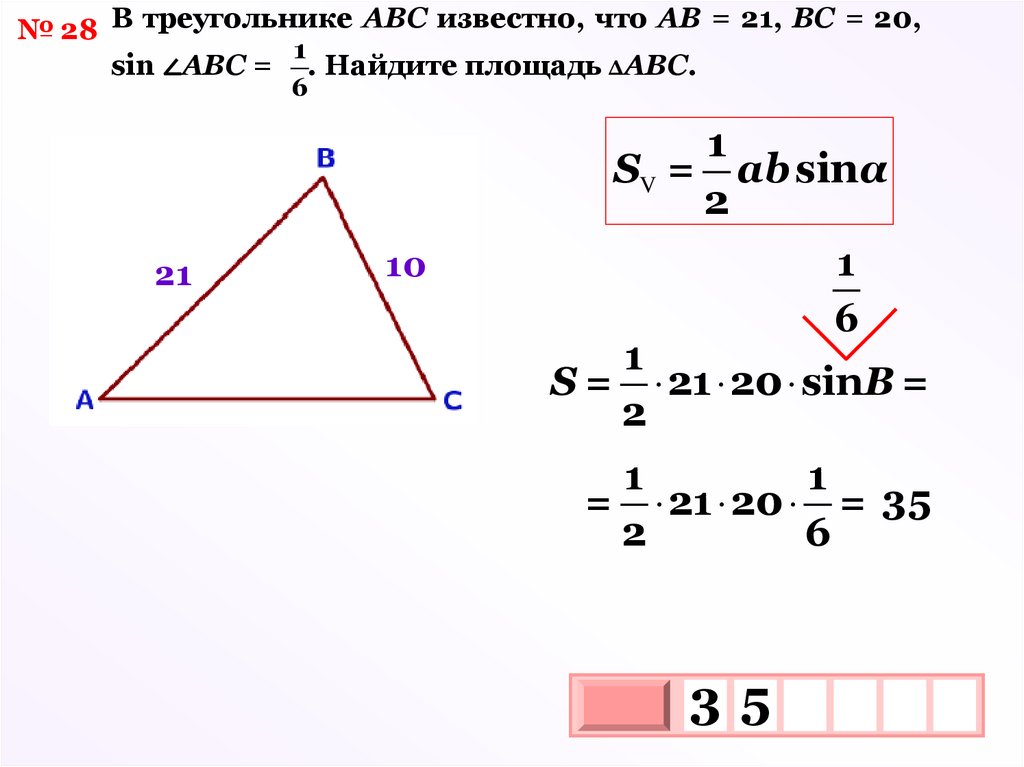
№ 28 В треугольнике АВС известно, что АВ = 21, ВС = 20,1
sin ∠АВС = . Найдите площадь ΔАВС.
6
1
SV = аb sinα
2
21
1
6
10
1
S = 21 20 sinВ =
2
1
1
= 21 20 = 35
2
6
35
3
10 х
х
64.
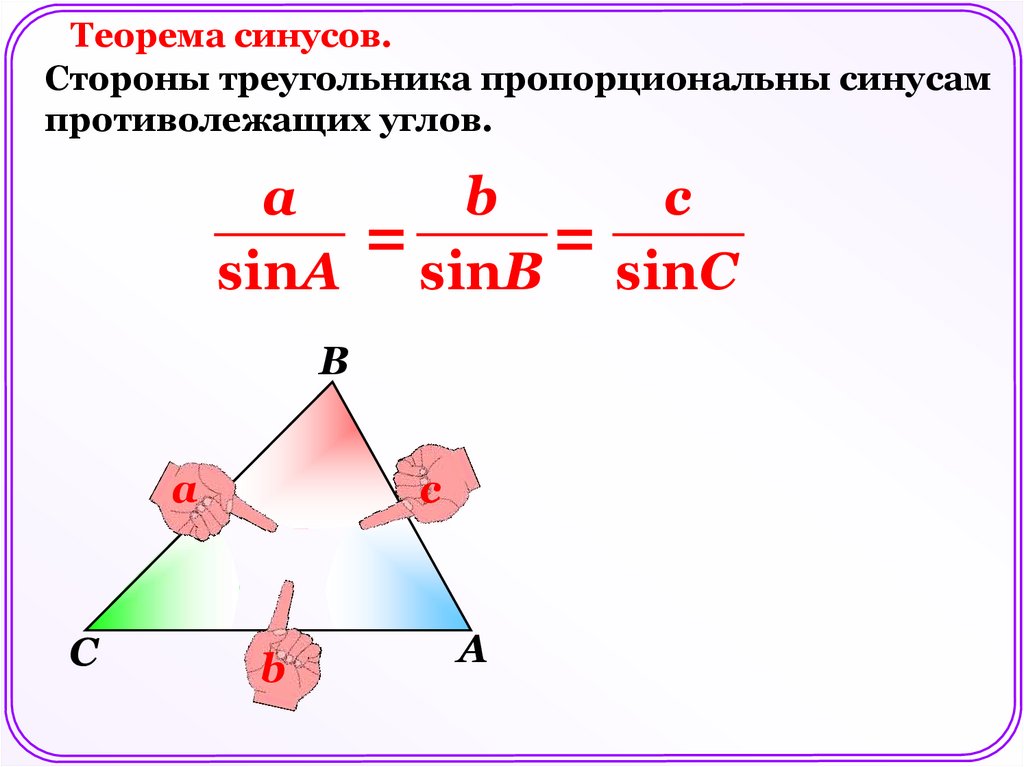
Теорема синусов.Стороны треугольника пропорциональны синусам
противолежащих углов.
а
b
с
=
=
sinА sinВ sinС
B
a
C
c
b
A
65.
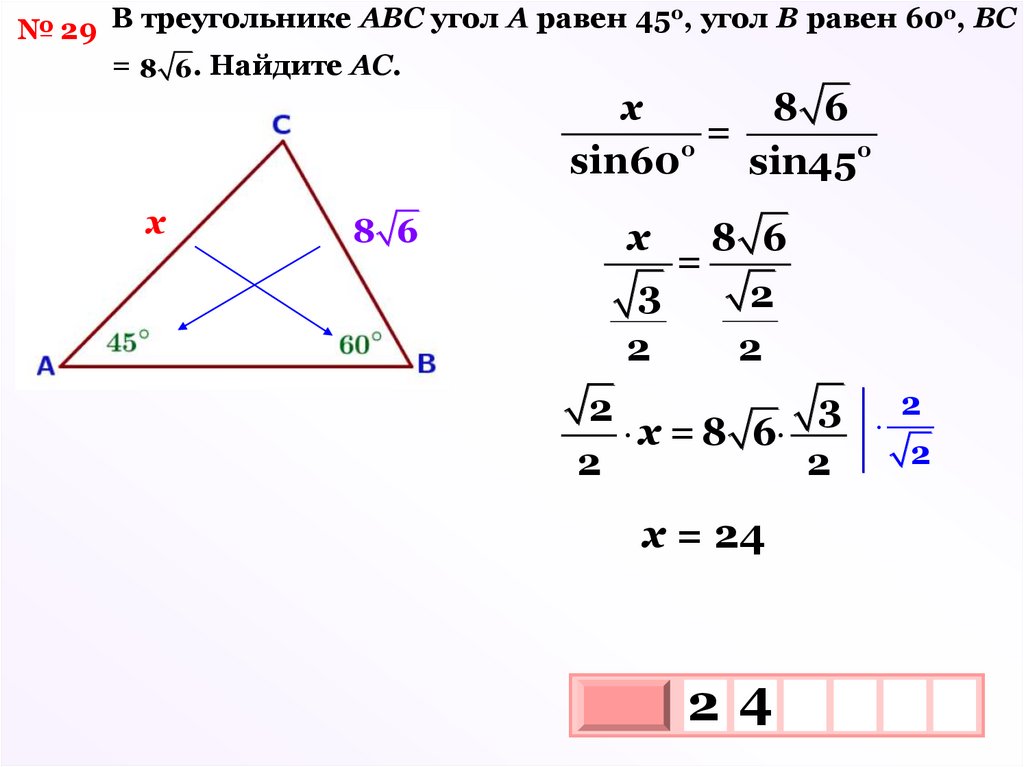
о, угол В равен 60о, ВСВ
треугольнике
АВС
угол
А
равен
45
№ 29
= 8 6. Найдите АС.
х
8 6
=
о
sin60
sin45о
х
8 6
х
8 6
=
3
2
2
2
3 2
2
х = 8 6
2
2
2
х = 24
24
3
10 х
х
66.
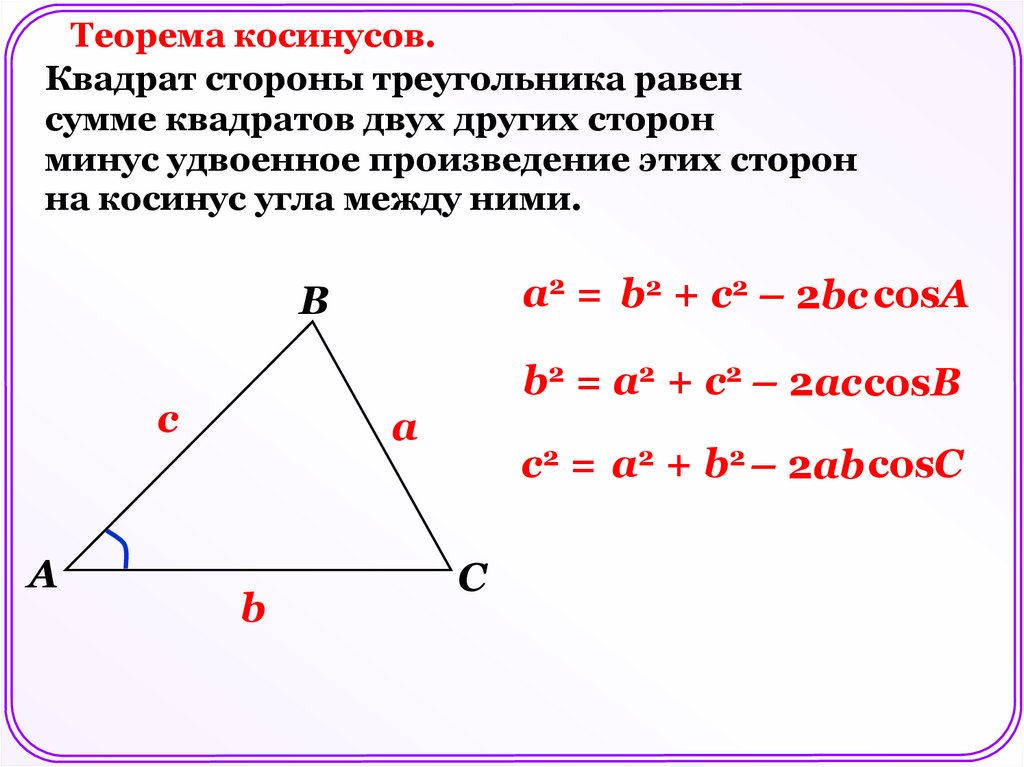
Теорема косинусов.Квадрат стороны треугольника равен
сумме квадратов двух других сторон
минус удвоенное произведение этих сторон
на косинус угла между ними.
a2 = b2 + c2 – 2bc cosA
B
c
A
b2 = a2 + c2 – 2accosB
a
b
c2 = a2 + b2 – 2ab cosC
C
67.
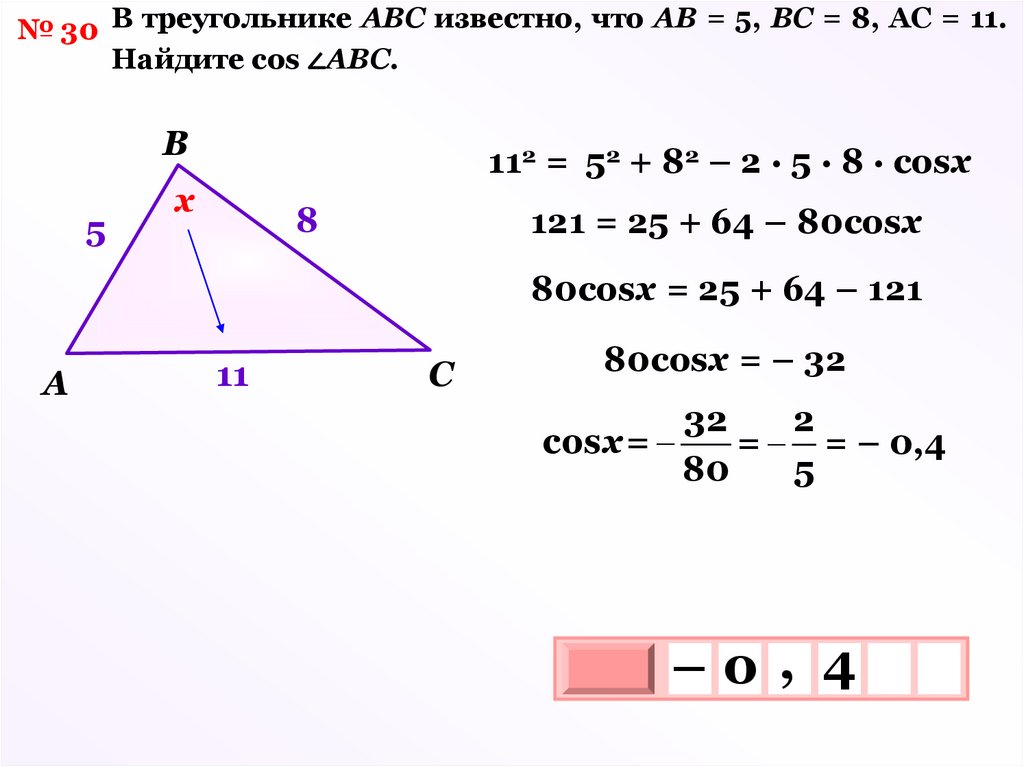
№ 30 В треугольнике АВС известно, что АВ = 5, ВС = 8, АС = 11.Найдите соs ∠АВС.
B
5
112 = 52 + 82 – 2 · 5 · 8 · соsх
х
8
121 = 25 + 64 – 80соsх
80соsх = 25 + 64 – 121
A
11
C
80соsх = – 32
32
2
соsх=
= = – 0,4
80
5
–0 , 4
3
10 х
х

 mathematics
mathematics








