Similar presentations:
Вписанная и описанная окружности. Прототип 16 задания ОГЭ
1.
Прототип 16 заданияОГЭ.
Вписанная и
описанная
окружности.
2.
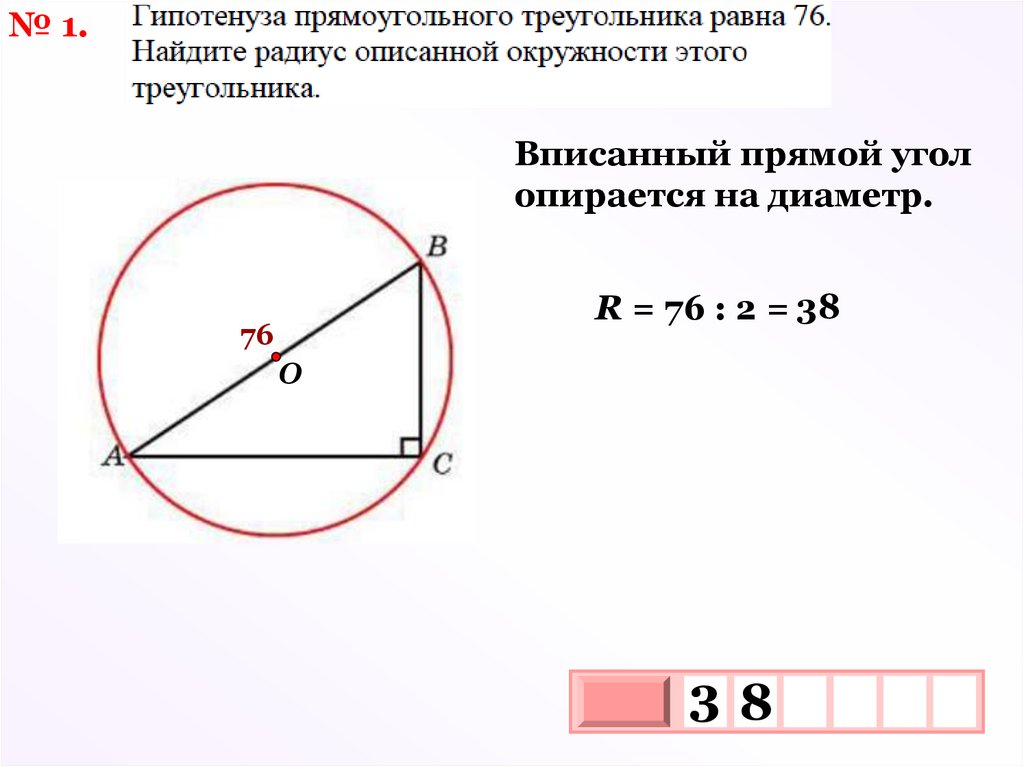
№ 1.Вписанный прямой угол
опирается на диаметр.
R = 76 : 2 = 38
76
О
38
3
10 х
х
3.
№ 2.Вписанный прямой угол
опирается на диаметр.
14
АВ = 14 · 2 = 28
О
28
3
10 х
х
4.
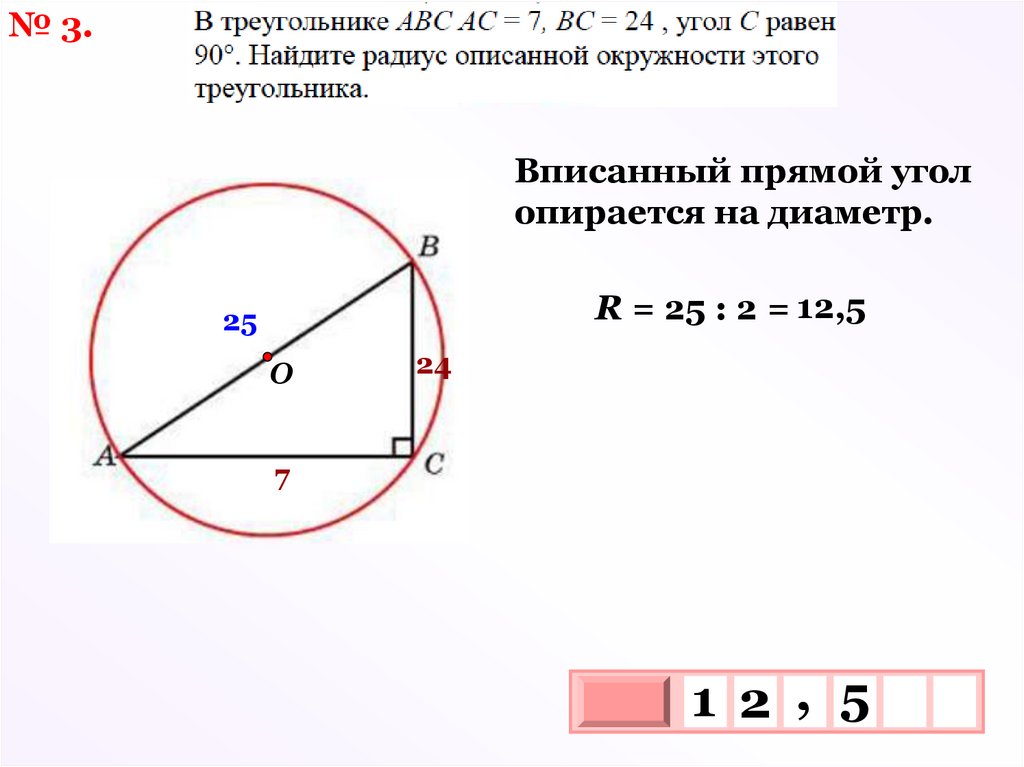
№ 3.Вписанный прямой угол
опирается на диаметр.
R = 25 : 2 = 12,5
25
О
24
7
1 2 , 5
3
10 х
х
5.
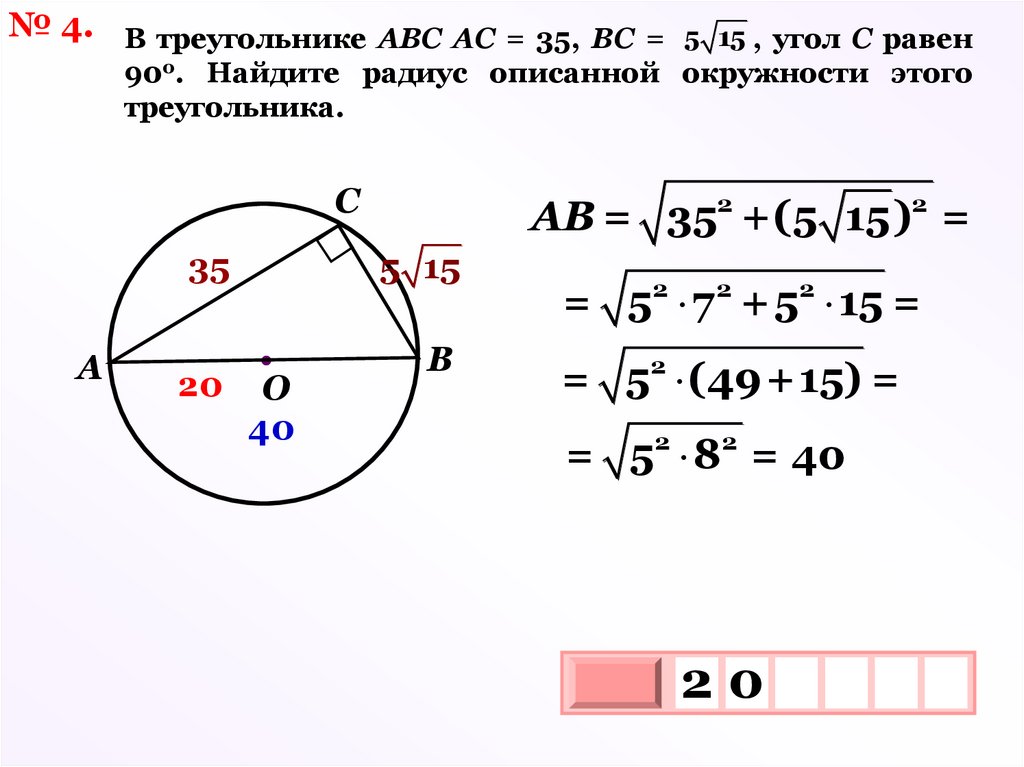
№ 4. В треугольнике АВС АС = 35, ВС = 5 15 , угол С равен90о. Найдите радиус описанной окружности этого
треугольника.
C
5 15
35
A
20
АВ = 352 +(5 15)2 =
O
40
B
= 52 7 2 + 52 15 =
= 5 (49+15) =
2
= 52 82 = 40
20
3
10 х
х
6.
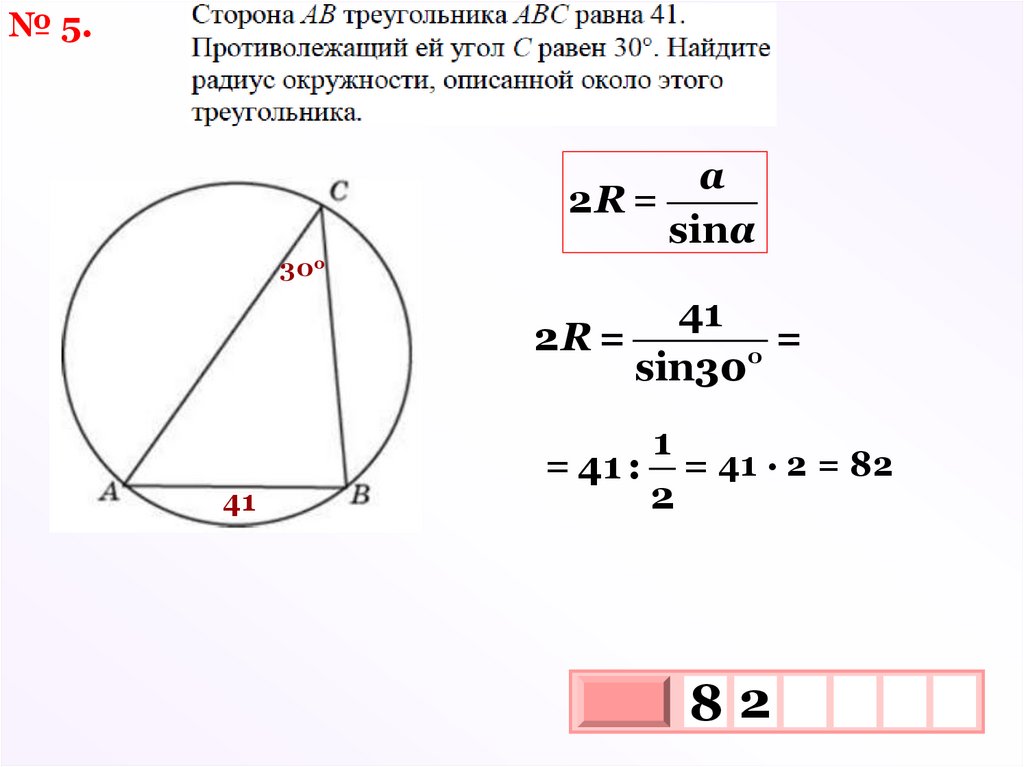
№ 5.a
2R =
sinα
30о
41
2R =
=
о
sin30
41
1
= 41 : = 41 · 2 = 82
2
82
3
10 х
х
7.
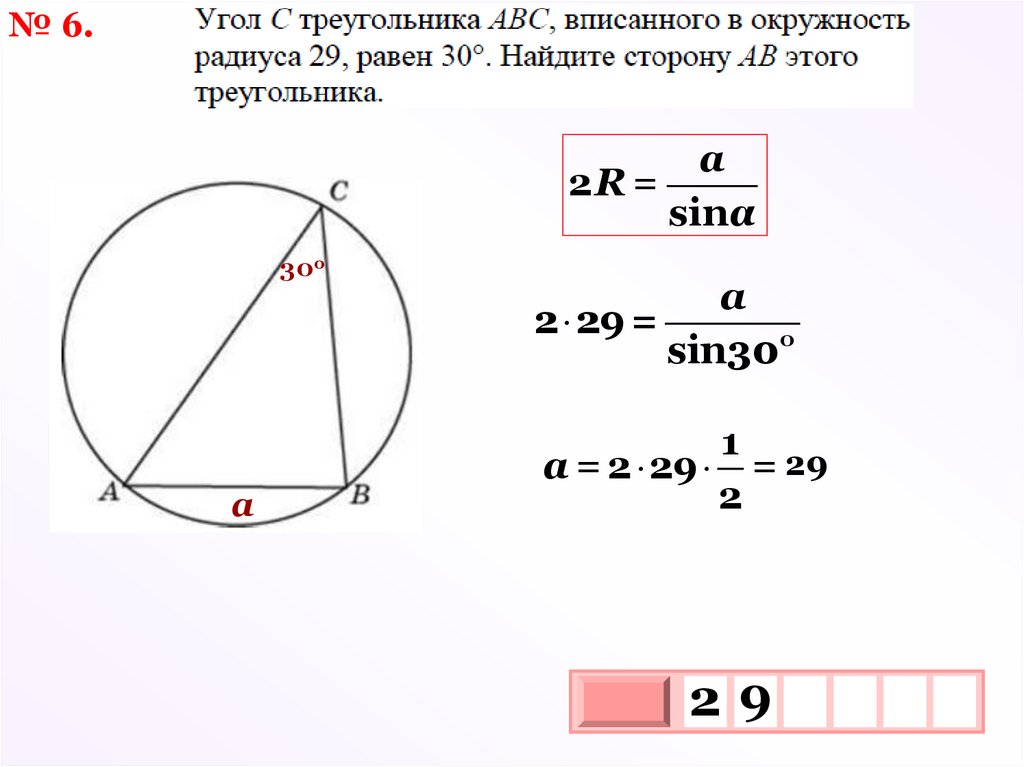
№ 6.a
2R =
sinα
30о
а
а
2 29 =
sin30о
1
а = 2 29 = 29
2
29
3
10 х
х
8.
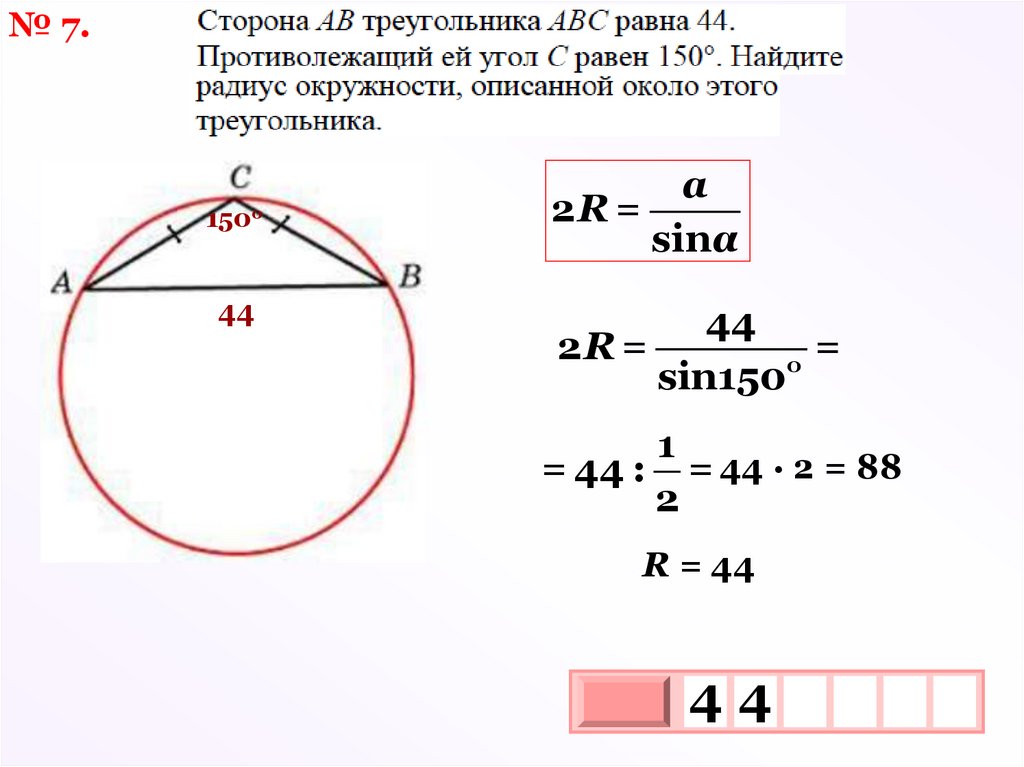
№ 7.150о
44
a
2R =
sinα
44
2R =
=
о
sin150
1
= 44 : = 44 · 2 = 88
2
R = 44
44
3
10 х
х
9.
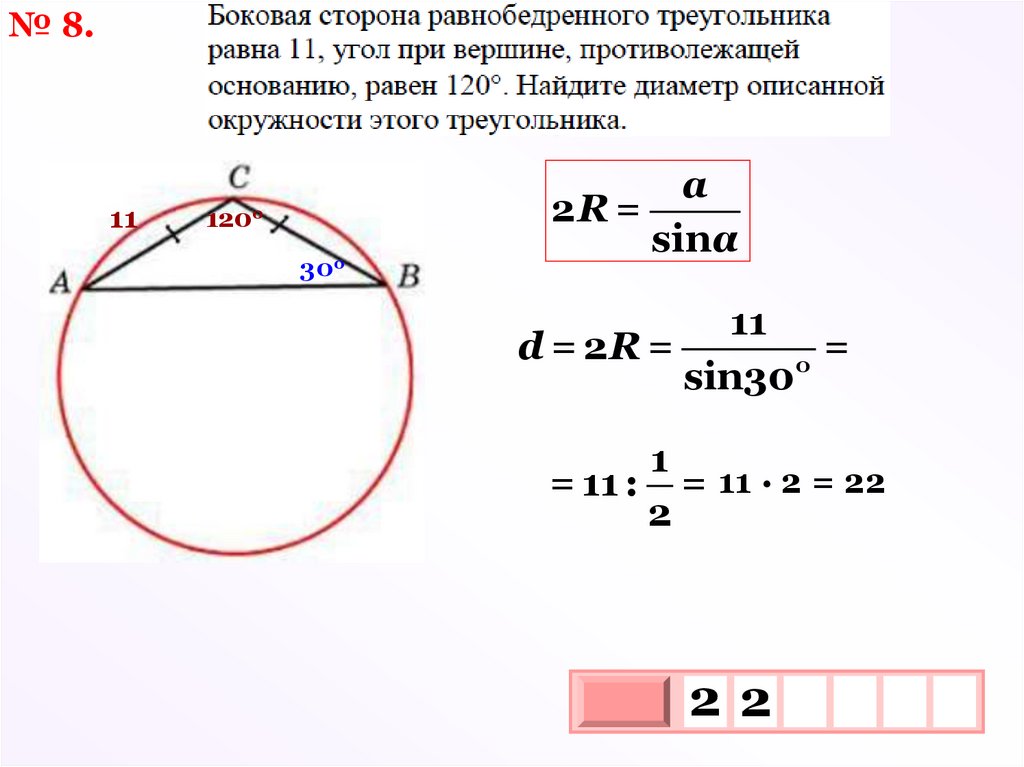
№ 8.11
120о
30о
a
2R =
sinα
11
d = 2R =
=
о
sin30
1
= 11 : = 11 · 2 = 22
2
22
3
10 х
х
10.
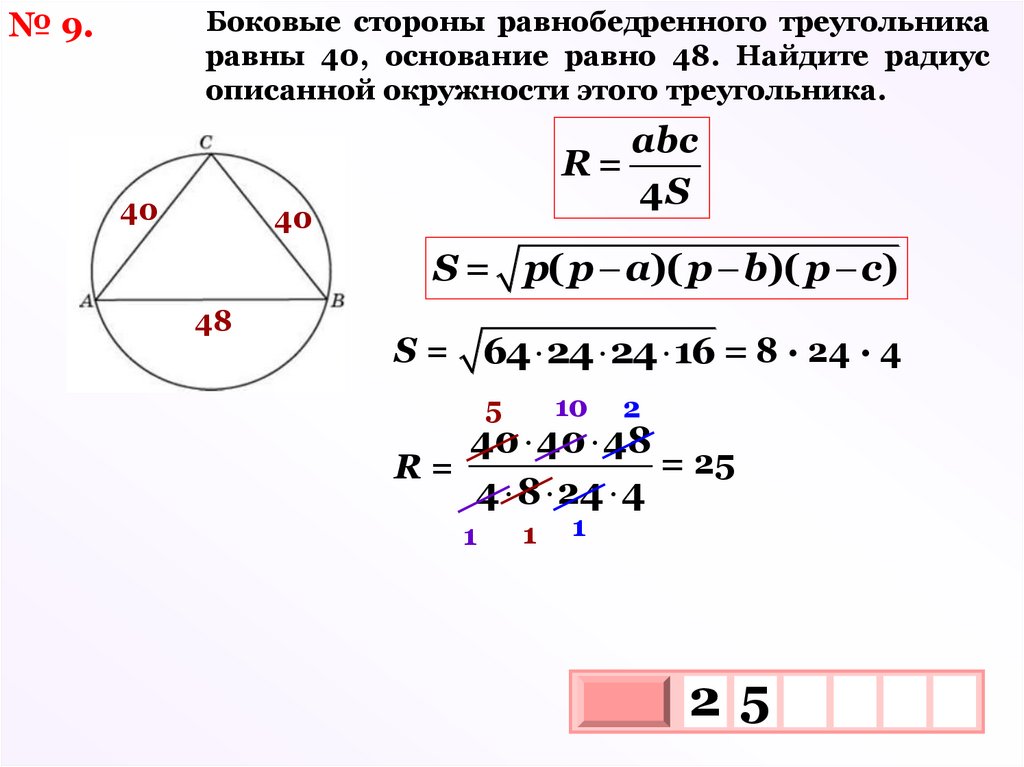
Боковые стороны равнобедренного треугольникаравны 40, основание равно 48. Найдите радиус
описанной окружности этого треугольника.
№ 9.
40
abc
R=
4S
40
S = р( р a)( р b)( р c)
48
S = 64 24 24 16 = 8 · 24 · 4
10
5
2
40 40 48
= 25
R=
4 8 24 4
1
1
1
25
3
10 х
х
11.
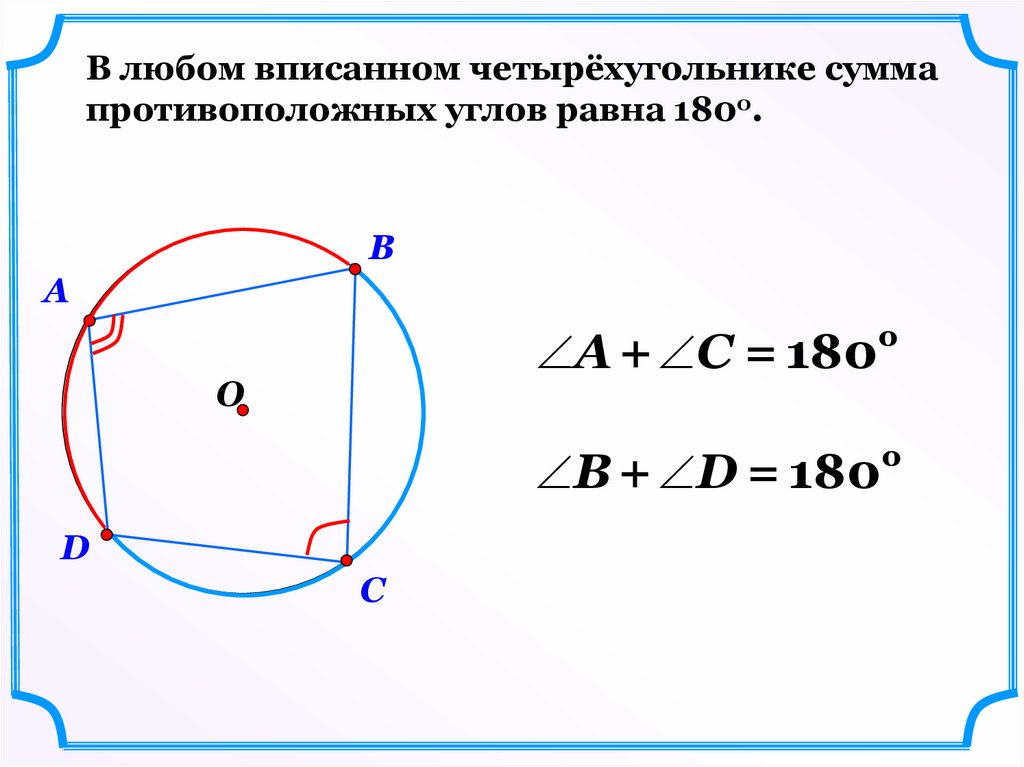
В любом вписанном четырёхугольнике суммапротивоположных углов равна 180о.
B
A
А + С = 180
O
0
В + D = 180
D
C
0
12.
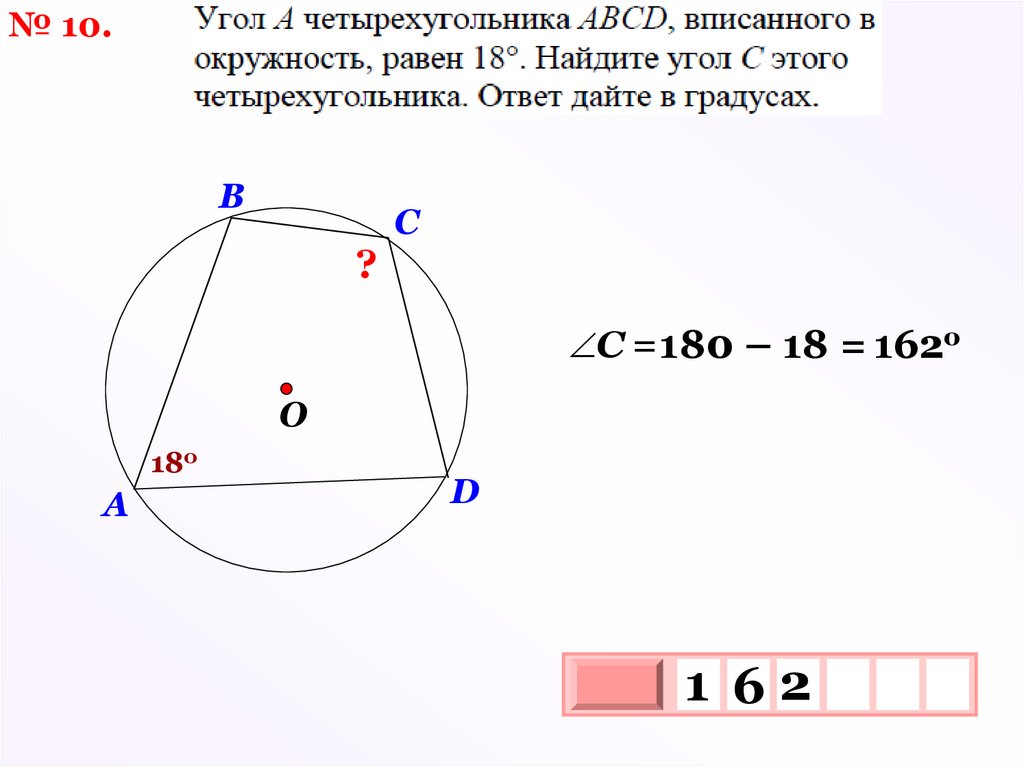
№ 10.B
?
C
С = 180 – 18 = 162о
O
180
A
D
1 62
3
10 х
х
13.
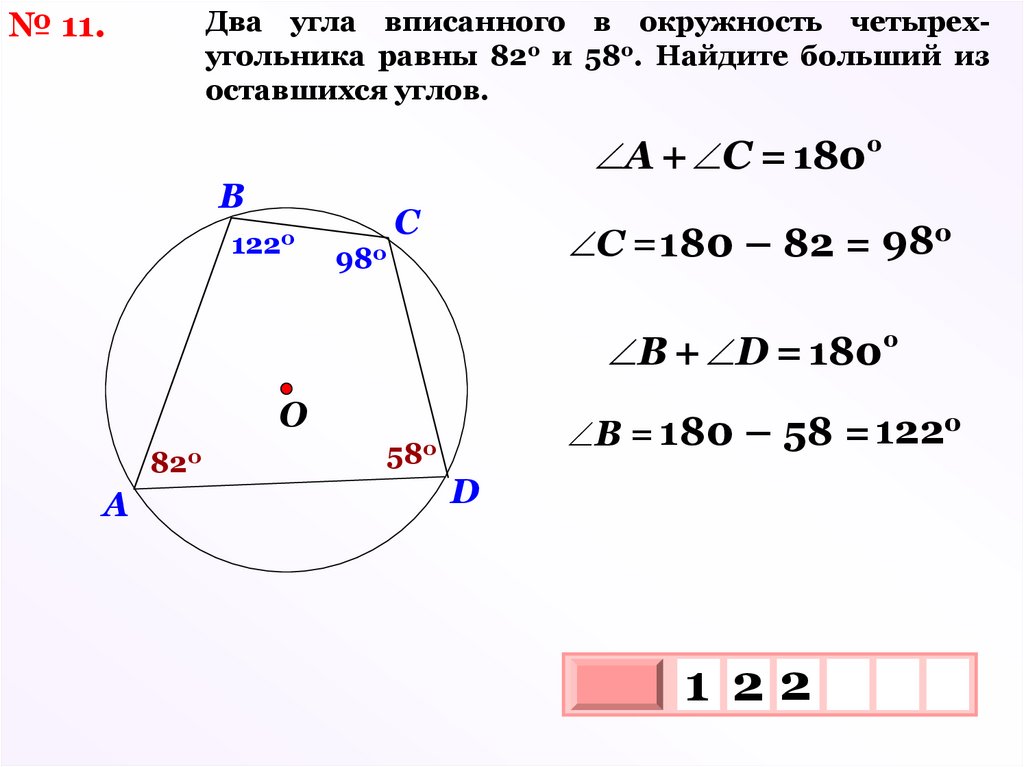
Два угла вписанного в окружность четырехугольника равны 82о и 58о. Найдите больший изоставшихся углов.
№ 11.
А + С = 1800
B
1220
C
С = 180 – 82 = 98о
980
В + D = 1800
O
820
A
В = 180 – 58 = 122о
580
D
1 22
3
10 х
х
14.
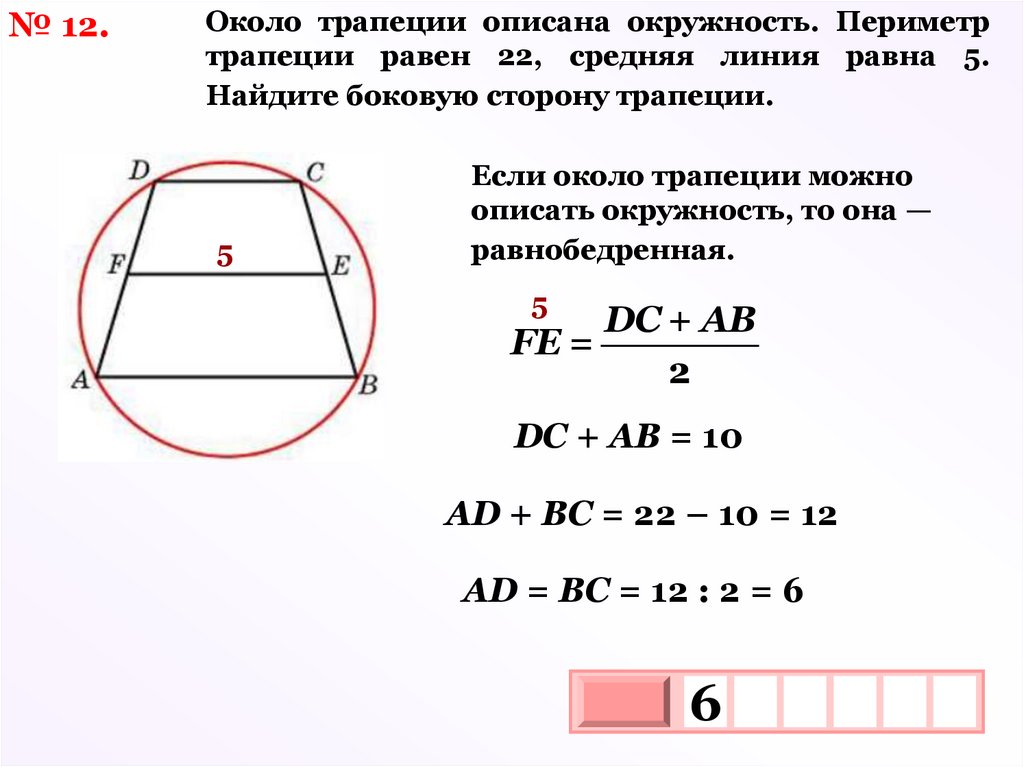
№ 12.Около трапеции описана окружность. Периметр
трапеции равен 22, средняя линия равна 5.
Найдите боковую сторону трапеции.
5
Если около трапеции можно
описать окружность, то она —
равнобедренная.
5
DC + AB
FE =
2
DC + АВ = 10
АD + ВС = 22 – 10 = 12
АD = ВС = 12 : 2 = 6
6
3
10 х
х
15.
Боковая сторона равнобедренной трапеции равнаее меньшему основанию, угол при основании
равен 60о , большее основание равно 12. Найдите
радиус описанной окружности этой трапеции.
№ 13.
хо
хо
60о
12
1
60 = 2 х
2
1
А = DB
2
хо
о
х = 60о
АB = 3х = 180о
АВ = d = 12
R=6
6
3
10 х
х
16.
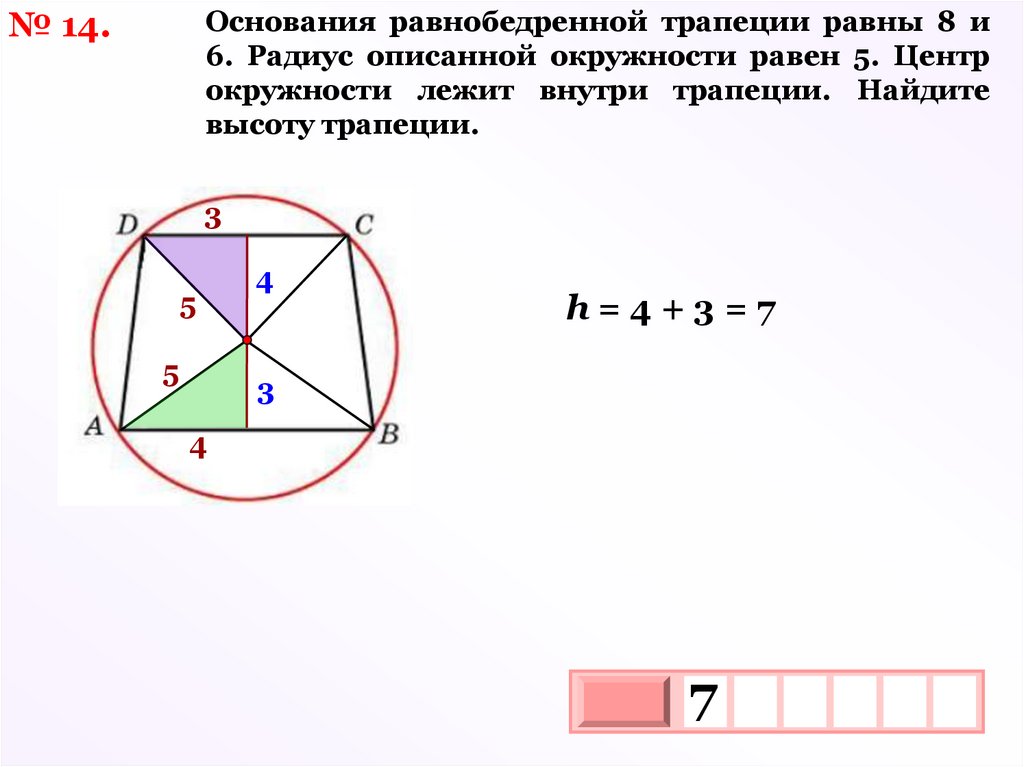
Основания равнобедренной трапеции равны 8 и6. Радиус описанной окружности равен 5. Центр
окружности лежит внутри трапеции. Найдите
высоту трапеции.
№ 14.
3
5
5
4
h=4+3=7
3
4
7
3
10 х
х
17.
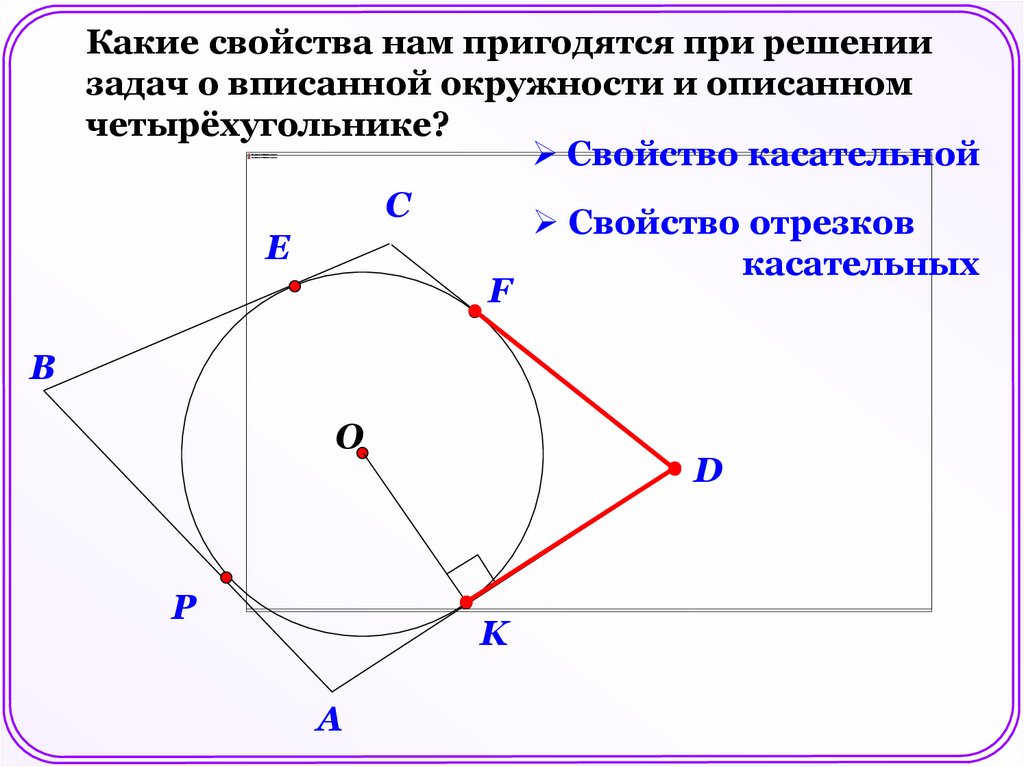
Какие свойства нам пригодятся при решениизадач о вписанной окружности и описанном
четырёхугольнике?
Свойство касательной
C
Свойство отрезков
E
касательных
F
B
O
P
D
K
A
18.
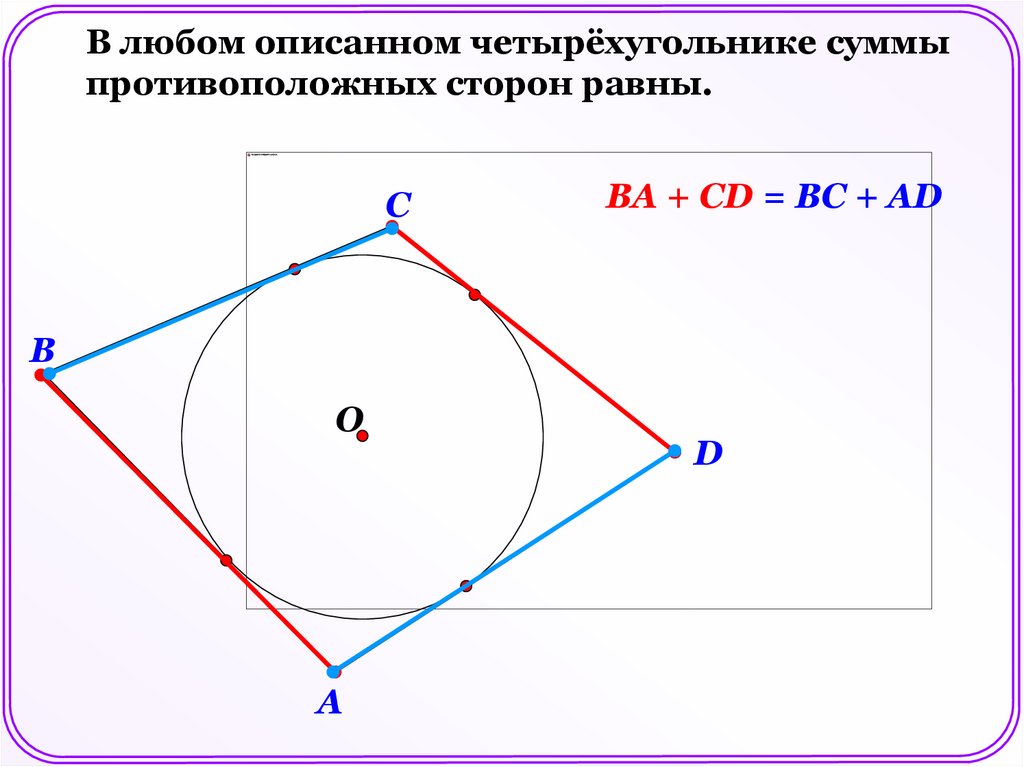
В любом описанном четырёхугольнике суммыпротивоположных сторон равны.
C
BA + CD = BC + AD
B
O
A
D
19.
№ 15.4
сумма 32
АВ + СD = АD + ВС
сумма 32
28
Средняя линия равна полусумме оснований
1 6
3
10 х
х
20.
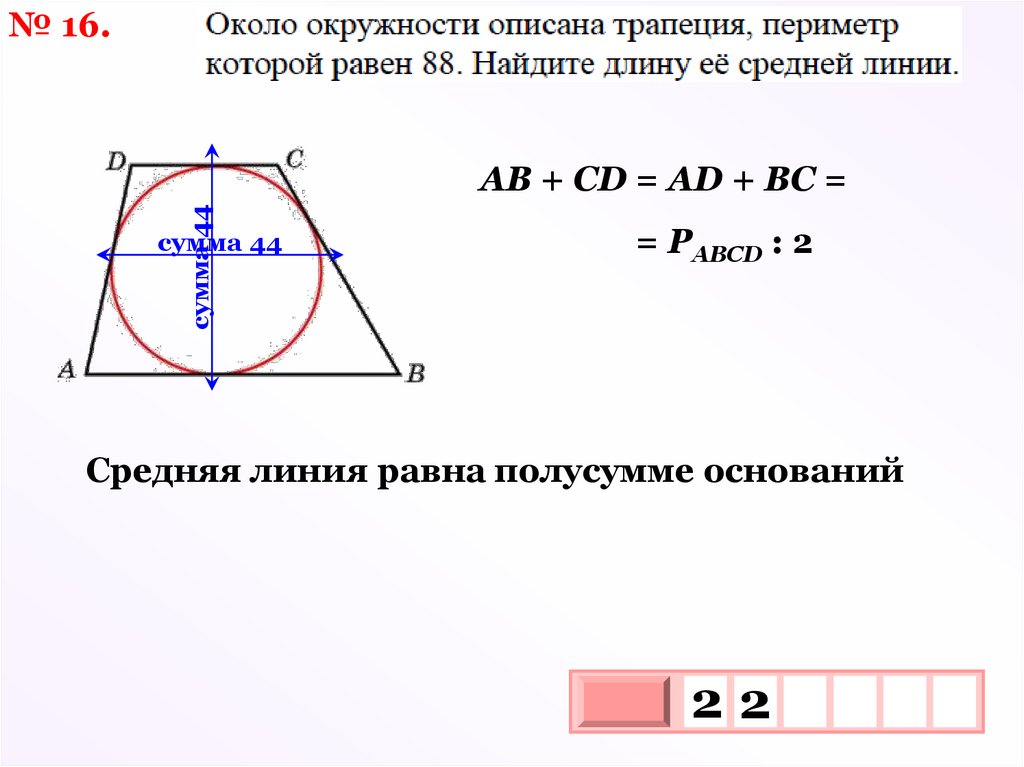
№ 16.сумма 44
АВ + СD = АD + ВС =
сумма 44
= РАВСD : 2
Средняя линия равна полусумме оснований
22
3
10 х
х
21.
№ 17.АВ + СD = АD + ВС
13
сумма 50
r
37
АD + BС = РАВСD : 2
r = АD : 2 = 13 : 2 = 6,5
6 , 5
3
10 х
х
22.
№ 18.АВ + СD = АD + ВС
14
6 + 14 = х + 2
х
2
АD = х = 18
6
1 8
3
10 х
х
23.
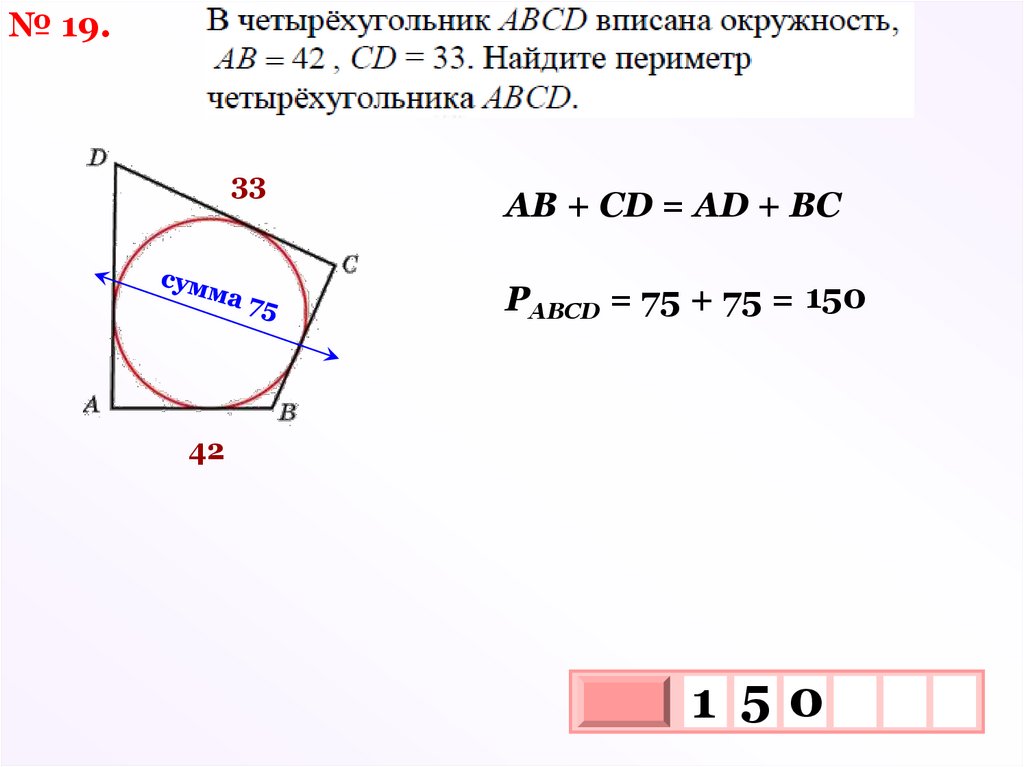
№ 19.33
АВ + СD = АD + ВС
РАВСD = 75 + 75 = 150
42
1 50
3
10 х
х
24.
№ 20.АВ + СD = АD + ВС
АВ + СD = РАВСD : 2
DС = 33 – 21 = 12
21
1 2
3
10 х
х
25.
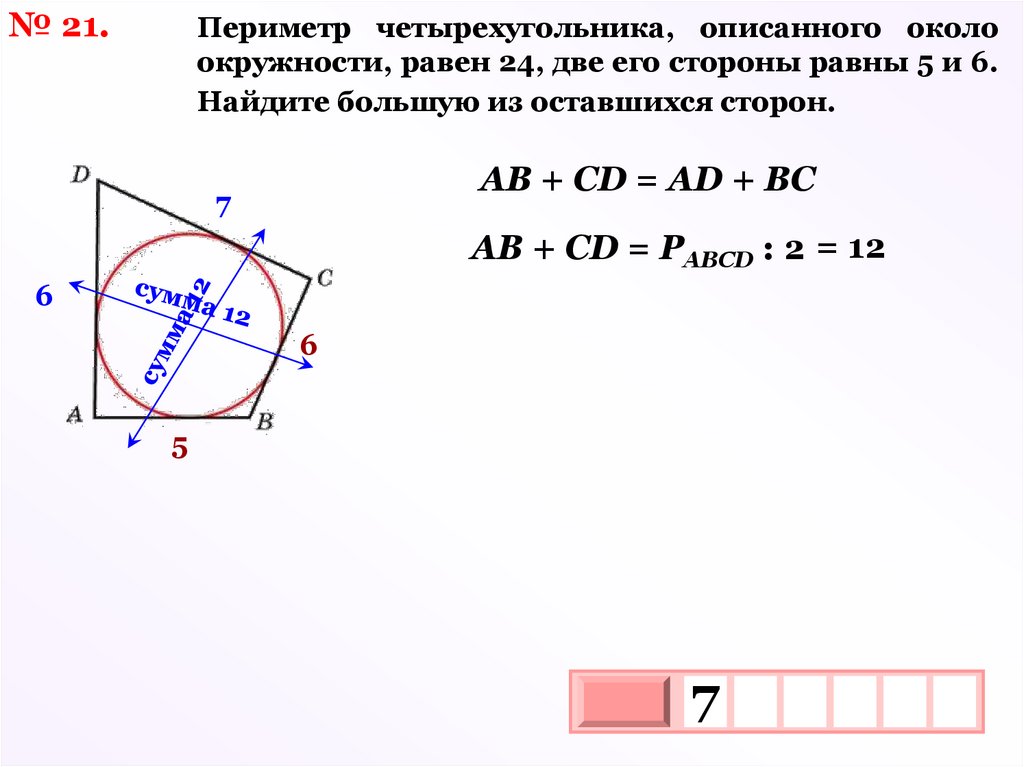
№ 21.Периметр четырехугольника, описанного около
окружности, равен 24, две его стороны равны 5 и 6.
Найдите большую из оставшихся сторон.
АВ + СD = АD + ВС
7
АВ + СD = РАВСD : 2 = 12
6
6
5
7
3
10 х
х
26.
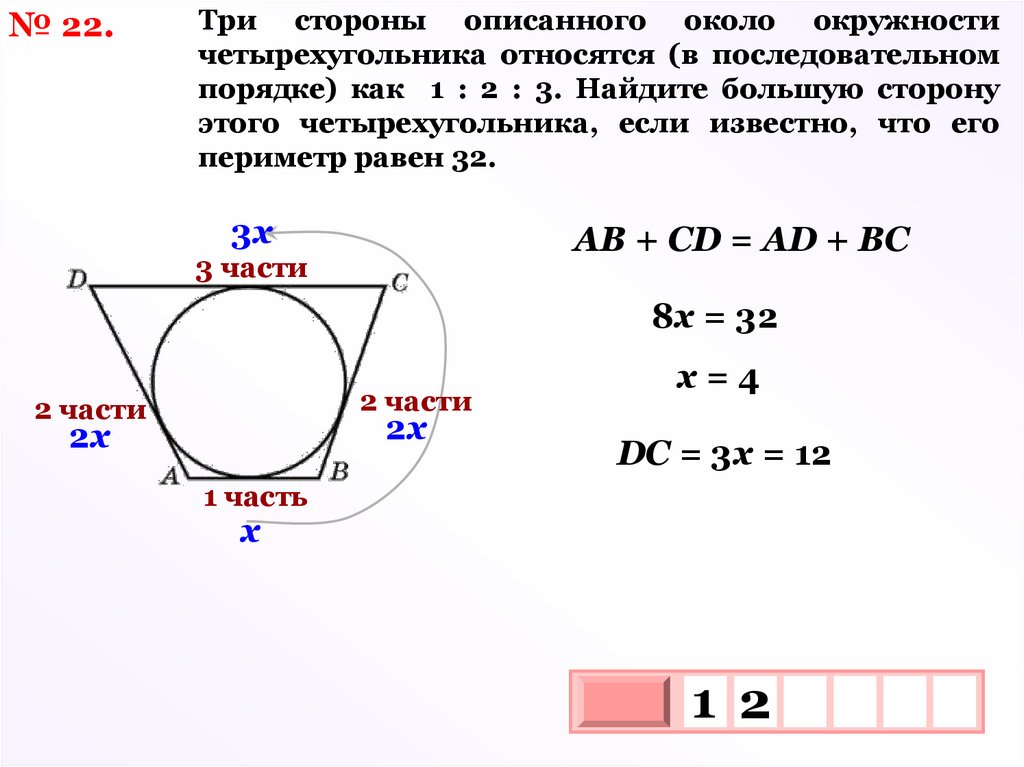
№ 22.Три стороны описанного около окружности
четырехугольника относятся (в последовательном
порядке) как 1 : 2 : 3. Найдите большую сторону
этого четырехугольника, если известно, что его
периметр равен 32.
3х
АВ + СD = АD + ВС
3 части
8х = 32
2 части
2 части
2х
2х
х=4
DC = 3х = 12
1 часть
х
1 2
3
10 х
х
27.
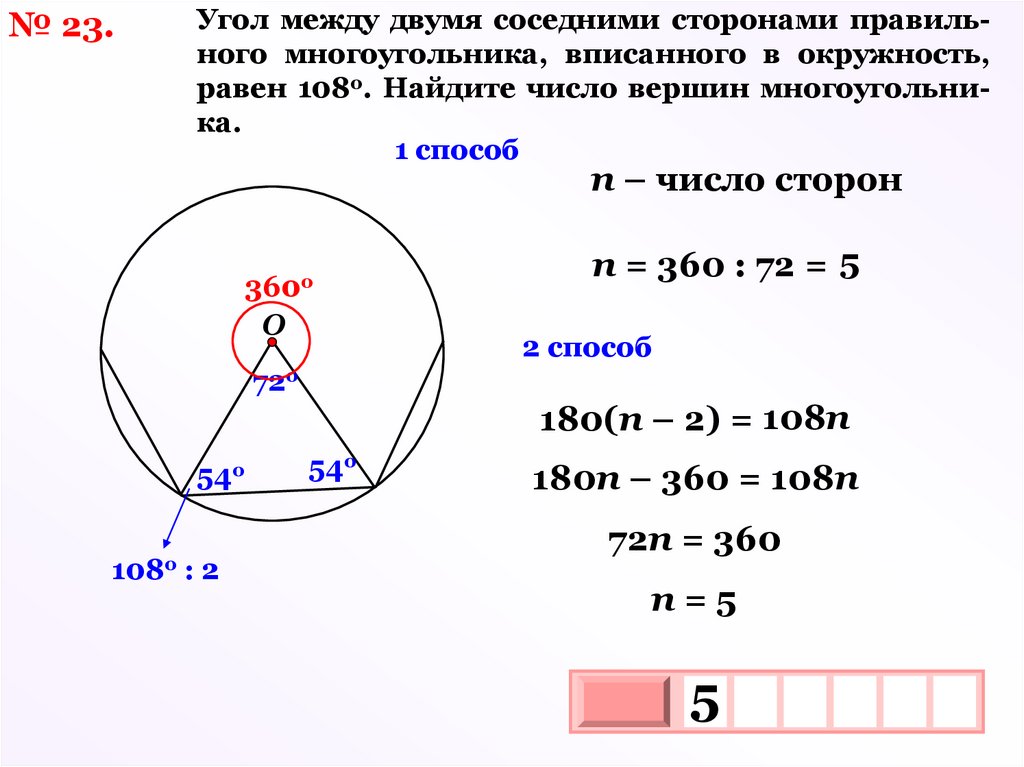
№ 23.Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность,
равен 108о. Найдите число вершин многоугольника.
1 способ
n – число сторон
360о
О
n = 360 : 72 = 5
2 способ
72о
180(n – 2) = 108n
54о
108о : 2
54о
180n – 360 = 108n
72n = 360
n=5
5
3
10 х
х
28.
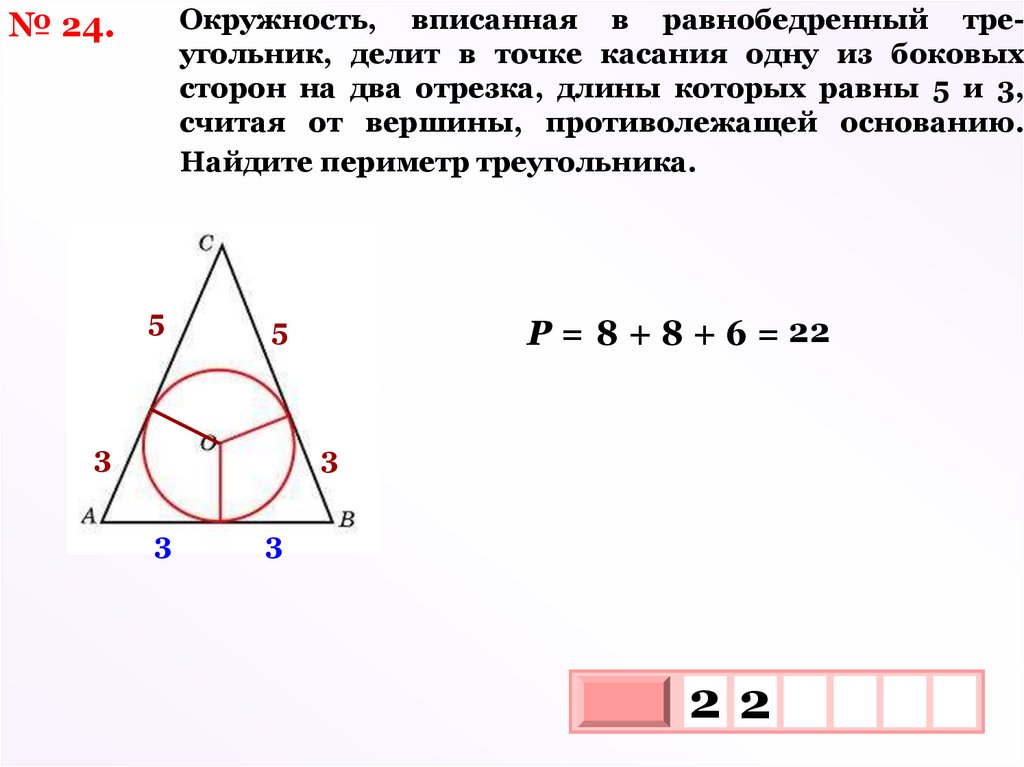
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковыхсторон на два отрезка, длины которых равны 5 и 3,
считая от вершины, противолежащей основанию.
Найдите периметр треугольника.
№ 24.
5
Р = 8 + 8 + 6 = 22
5
3
3
3
3
22
3
10 х
х
29.
Формула площади треугольника.а
b
R
c
abc
S
4R
30.
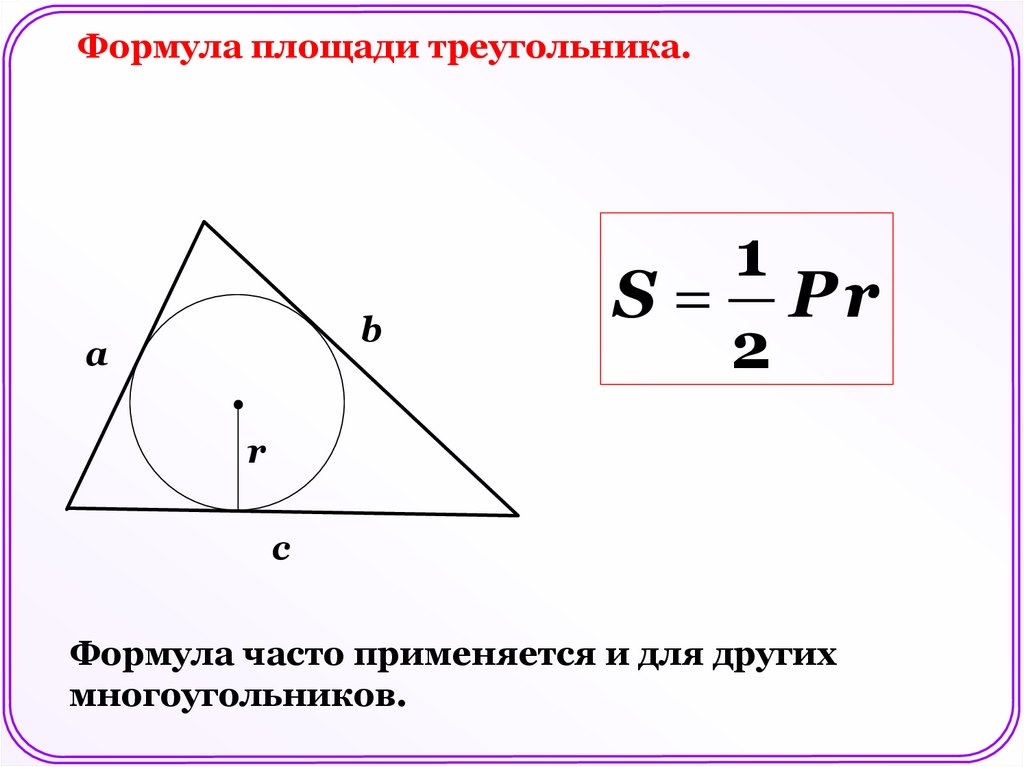
Формула площади треугольника.b
а
1
S Pr
2
r
c
Формула часто применяется и для других
многоугольников.
31.
№ 25 Периметр треугольника равен 34, одна из сторон равна10, а радиус вписанной в него окружности равен 4.
Найдите площадь этого треугольника.
1
S = Pr
2
4
10
1
S = 34 4 = 68
2
68
3
10 х
х









 mathematics
mathematics








