Similar presentations:
Задание №15 базового уровня. Равнобедренный треугольник: вычисление углов
1.
Практикум №2 по решениюпланиметрических задач
(базовый уровень)
Разработано учителем математики
МОУ «СОШ» п. Аджером
Корткеросского района Республики Коми
Мишариной Альбиной Геннадьевной
2.
Задание №15 базового уровняРавнобедренный треугольник:
вычисление углов
3. Содержание
Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №8
Задача №9
Задача №10
Задача №11
Задача №12
Задача №13
Задача №14
Задача №15
Задача №16
Задача №17
Задача №18
•Задачи для сам. решения
4. Задача №1
В равнобедренном треугольнике ABC боковыестороны AB = BC = 5, медиана BM = 4. Найдите cos∠BAC.
Решение. В равнобедренном треугольнике медиана
опущенная на основание является высотой и
биссектрисой. Рассмотрим прямоугольный
треугольник ABM. По теореме Пифагора
найдём AM:
AM=3. Найдём cos∠BAC:
5. Задача №2
В треугольнике АВС АС=BС=8, АВ=8 . Найдите cosA .Решение.
Треугольник АВС равносторонний, значит,
высота СН делит
основание АВ пополам.
6. Задача №3
В треугольнике АВС АС=ВС, высота СН равна 7, АВ=48.Найдите sinA.
Решение.
Треугольник АВС равнобедренный, значит,
высота СН делит основание АВ пополам.
7. Задача №4
В треугольнике ABC известно, что AB = BC = 20, АС =32 . Найдите синус угла ВАС.
Решение.
Треугольник ABC равнобедренный, так как AB = BC,
найдём по теореме Пифагора высоту, выходящую из вершины В,
она будет равна:
ВН² = АВ² - АН² = 400 – 256 = 144 = 12²
Синус - это отношение противолежащего катета к
гипотенузе: sinBAC = BH:AB = 12:20 = 0,6
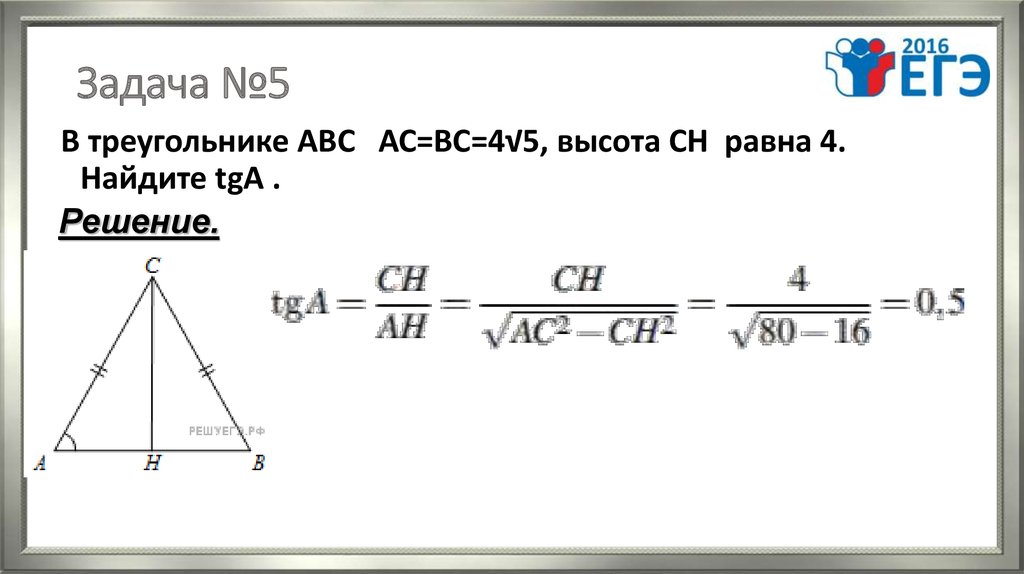
8. Задача №5
В треугольнике АВС АС=ВС=4√5, высота СН равна 4.Найдите tgA .
Решение.
9. Задача №6
В треугольнике АВС АВ=ВС, АН – высота, sinBAC=7/5.Найдите sinBAH.
Решение. Треугольник ABC равнобедренный, значит,
углы BAC и ABH равны как углы при его
основании.
10. Задача №7
В треугольнике АВС АВ=ВС, АН – высота, sinBAC=0,1.Найдите cosBAH.
Решение.
Треугольник ABC равнобедренный,
значит, углы BAC и ABH равны как углы
при его основании.
11. Задача №8
В треугольнике АВС АВ=ВС, АН – высота, sinBAC=4/√17.Найдите tgBAH.
Решение. Треугольник ABC равнобедренный, значит,
углы BAC и ABH равны как углы при его
основании.
.
12. Задача №9
В треугольнике АВС АВ=ВС, АН – высота и равна 20,AB=25. Найдите cosBAC.
Решение. Треугольник ABC равнобедренный, значит,
углы BAC и ABH равны как углы при его
основании.
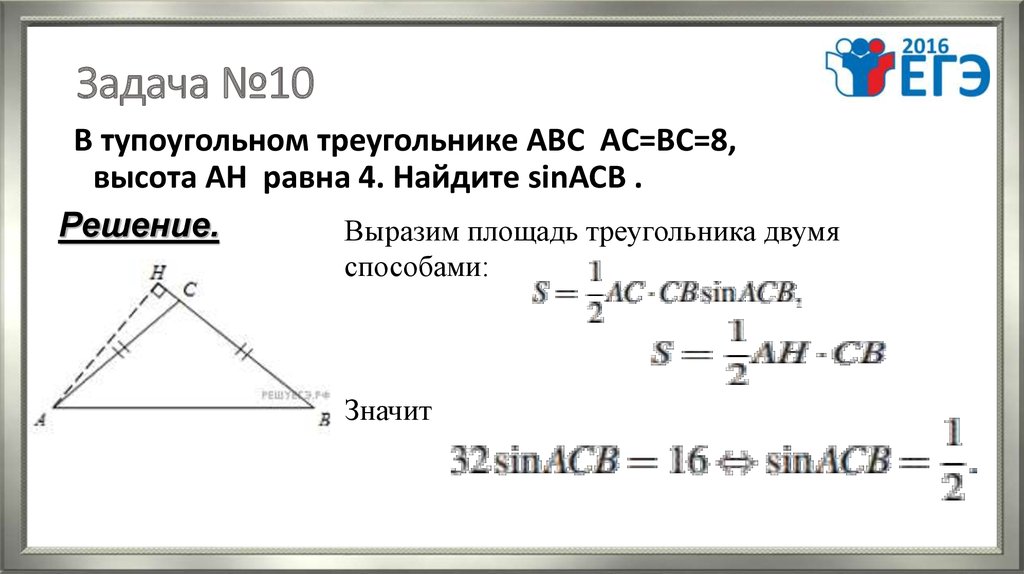
13. Задача №10
В тупоугольном треугольнике АВС АC=ВС=8,высота АН равна 4. Найдите sinACB .
Решение.
Выразим площадь треугольника двумя
способами:
Значит
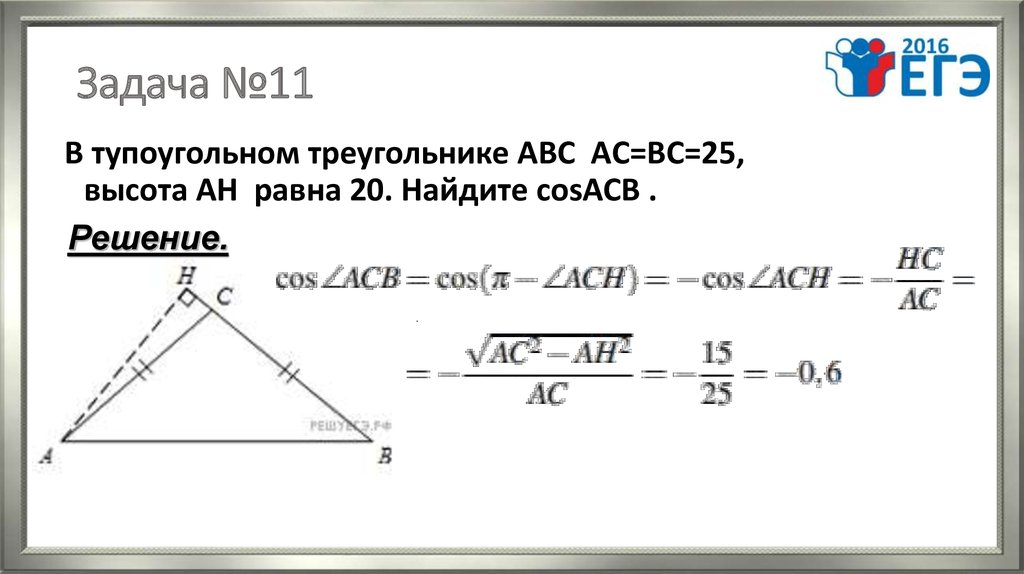
14. Задача №11
В тупоугольном треугольнике АВС АC=ВС=25,высота АН равна 20. Найдите cosACB .
Решение.
.
15. Задача №12
В тупоугольном треугольнике АВС АC=ВС=25, АН-высота,СН=20. Найдите sinACB .
Решение.
.
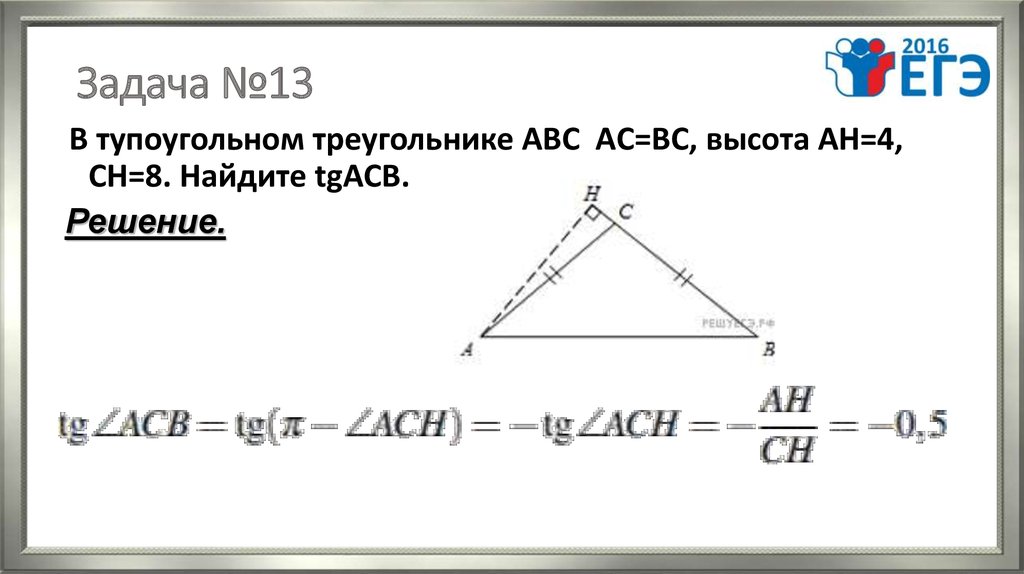
16. Задача №13
В тупоугольном треугольнике АВС АC=ВС, высота АН=4,СН=8. Найдите tgACB.
Решение.
17. Задача №14
В треугольнике АВС АС=ВС, высота АН равна 24, ВН=7.Найдите cosBAC.
Решение. Треугольник ABC равнобедренный, значит,
углы BAC и ABH равны как углы при его
основании.
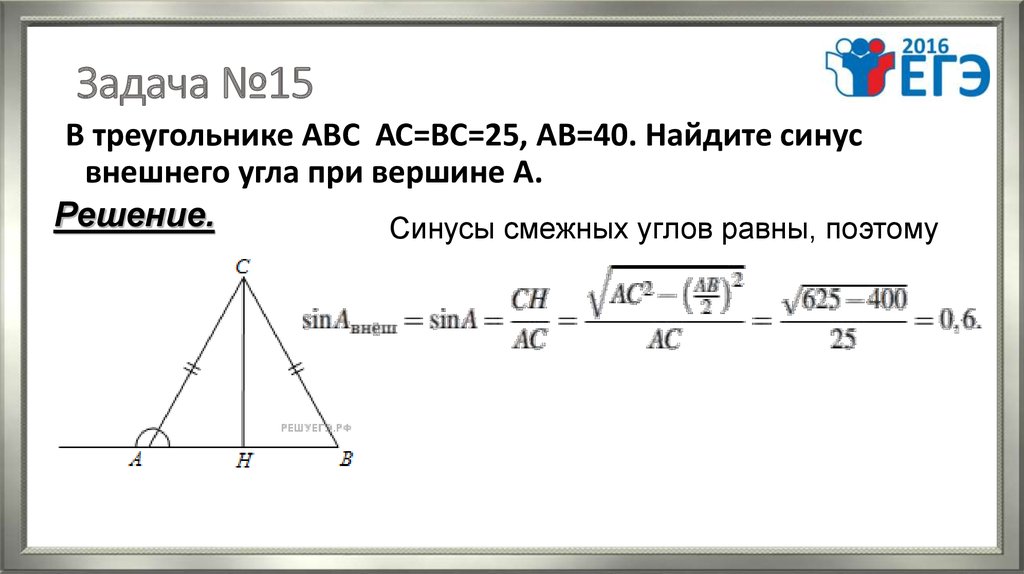
18. Задача №15
В треугольнике АВС АС=ВС=25, AB=40. Найдите синусвнешнего угла при вершине А.
Решение.
Синусы смежных углов равны, поэтому
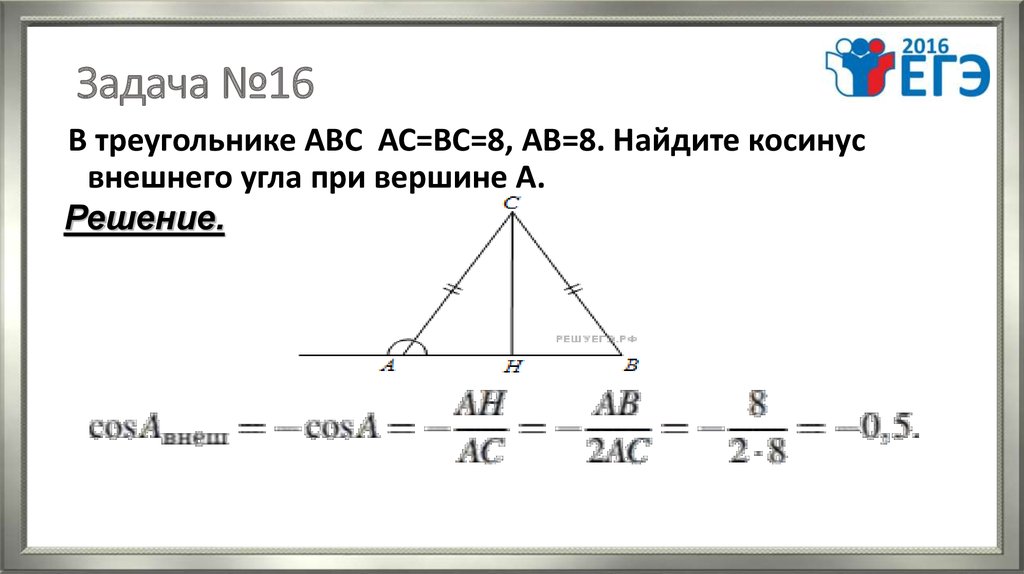
19. Задача №16
В треугольнике АВС АС=ВС=8, AB=8. Найдите косинусвнешнего угла при вершине А.
Решение.
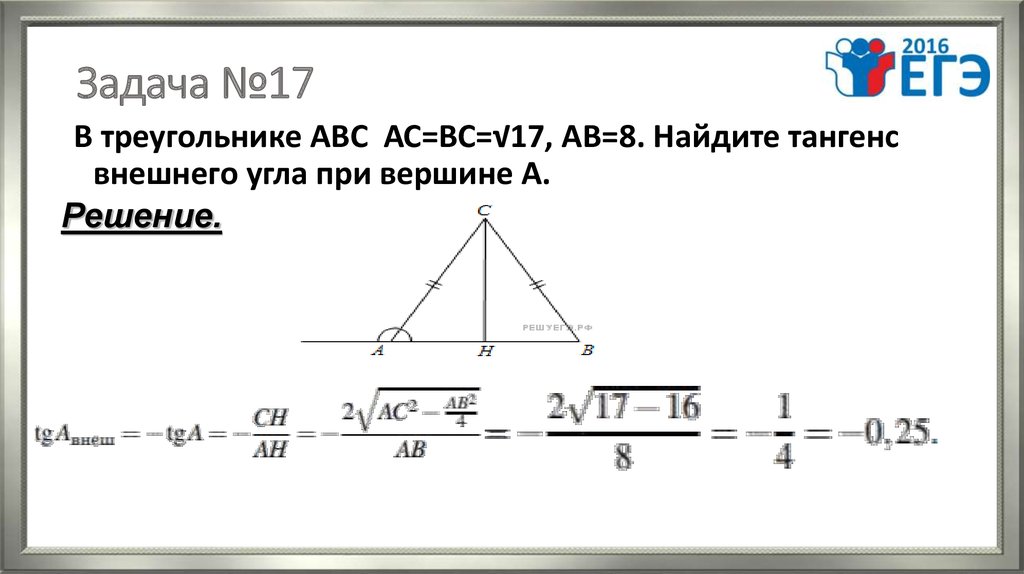
20. Задача №17
В треугольнике АВС АС=ВС=√17, AB=8. Найдите тангенсвнешнего угла при вершине А.
Решение.
21. Задача №18
Один угол равнобедренного треугольника на 90° большедругого. Найдите меньший угол. Ответ дайте в градусах.
Решение.
Т.к. треугольник равнобедренный, то углы при его основании равны.
Обозначим за х меньший угол, тогда больший угол равен (х+90).
Значит 2х+(х+90)=180 => 3х=90 ; х=30
22.
Задачидля самостоятельного
решения
23. Задача №2 Решите самостоятельно
1)2)
3)
4)
5)
В треугольнике АВС
В треугольнике АВС
В треугольнике АВС
В треугольнике АВС
В треугольнике АВС
АС=BС=20, АВ=10. Найдите cosA .
АС=BС=5, АВ=4. Найдите cosA .
АС=BС=12, АВ=18. Найдите cosA .
АС=BС=9√5, АВ=18 . Найдите tgA .
АС=BС=9√2, АВ=18 . Найдите tgA .
24. Задача №3 Решите самостоятельно
1) Задание 15 № 32641. В треугольнике ABC10, АВ=10√21. Найдите sinA.
2) Задание 15 № 32645. В треугольнике ABC
АВ=12√6. Найдите sinA.
3) Задание 15 № 32653. В треугольнике ABC
45, АВ=10√19 . Найдите sinA.
4) Задание 15 № 32663. В треугольнике ABC
3, АВ=2√7 . Найдите sinA .
, высота CH равна
, высота CH равна 3,
, высота CH равна
, высота CH равна
25. Задача №5 Решите самостоятельно
1) В треугольнике АВСНайдите tgA .
2) В треугольнике АВС
Найдите tgA .
3) В треугольнике АВС
Найдите tgA .
4) В треугольнике АВС
Найдите tgA .
АС=ВС=5√5, высота СН равна 5.
АС=ВС=2√61, высота СН равна 12.
АС=ВС=√5, высота СН равна 2.
АС=ВС=7√5, высота СН равна 14.
26. Задача №6 Решите самостоятельно
1) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=√3/2.Найдите sinBAH.
2) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=
√51/10. Найдите sinBAH.
3) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=
√19/10. Найдите sinBAH.
4) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=
√91/10. Найдите sinBAH.
27. Задача №7 Решите самостоятельно
1) В треугольнике АВСНайдите cosBAH.
2) В треугольнике АВС
Найдите cosBAH.
3) В треугольнике АВС
Найдите cosBAH.
4) В треугольнике АВС
Найдите cosBAH.
АВ=ВС, АН – высота, sinBAC=0,51.
АВ=ВС, АН – высота, sinBAC=0,27.
АВ=ВС, АН – высота, sinBAC=0,99
АВ=ВС, АН – высота, sinBAC=0,18.
28. Задача №8 Решите самостоятельно
1) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=5/13.Найдите tgBAH.
2) В треугольнике АВС АВ=ВС, АН –
высота, sinBAC=40/41. Найдите tgBAH.
3) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=4/5.
Найдите tgBAH.
4) В треугольнике АВС АВ=ВС, АН – высота, sinBAC=2/√13.
Найдите tgBAH.
29. Задача №10 Решите самостоятельно
1) В тупоугольном треугольнике АВС АC=ВС=5,высота АН равна 1. Найдите sinACB
2) В тупоугольном треугольнике АВС АC=ВС=14,
высота АН равна 7. Найдите sinACB
3) В тупоугольном треугольнике АВС АC=ВС=20,
высота АН равна 5. Найдите sinACB
30. Задача №15 Решите самостоятельно
1) В треугольнике АВС АС=ВС=25, AB=48. Найдите синусвнешнего угла при вершине А.
2) В треугольнике АВС АС=ВС=5, AB=2√21. Найдите синус
внешнего угла при вершине А.
3) В треугольнике АВС АС=ВС=2, AB=2√3. Найдите синус
внешнего угла при вершине А.
31. Задача №18 Решите самостоятельно
1) Один угол равнобедренного треугольника на 141°больше другого. Найдите меньший угол. Ответ дайте в
градусах.
2) Один угол равнобедренного треугольника на 165°
больше другого. Найдите меньший угол. Ответ дайте в
градусах.
3) Один угол равнобедренного треугольника на 96°
больше другого. Найдите меньший угол. Ответ дайте в
градусах.
32. Интернет источники
Шаблон подготовила учитель русского языка и литературы Тихонова Надежда Андреевна• https://fotki.yandex.ru/next/users/nata-komiati/album/159853/view/688546?page=5
• https://fotki.yandex.ru/next/users/nata-komiati/album/159853/view/688553?page=5
• https://fotki.yandex.ru/next/users/nata-komiati/album/158683/view/665734?page=3
• «Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа:
http://mathb.reshuege.ru
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
http://asa.my1.ru/_pu/0/90580308.png
























 mathematics
mathematics








