Подготовка к контрольной работе по геометрии

1.

04.12.2023
К л а с с н а я р а б о т а.
Подготовка к
контрольной работе

2.

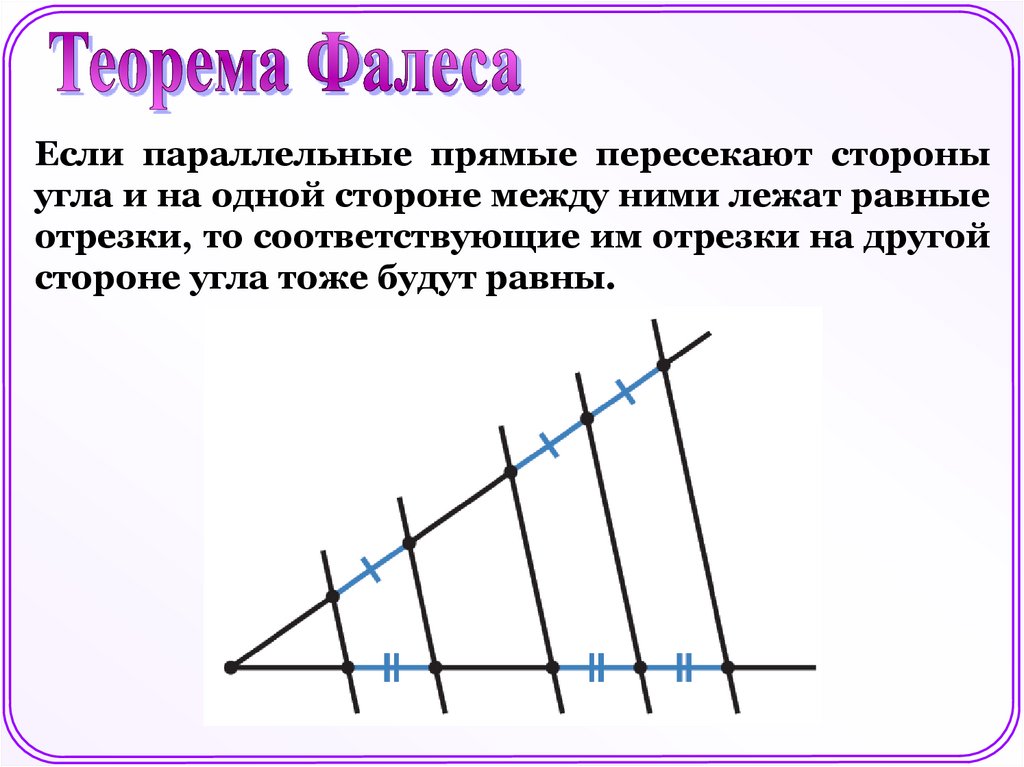
Если параллельные прямые пересекают стороны
угла и на одной стороне между ними лежат равные
отрезки, то соответствующие им отрезки на другой
стороне угла тоже будут равны.

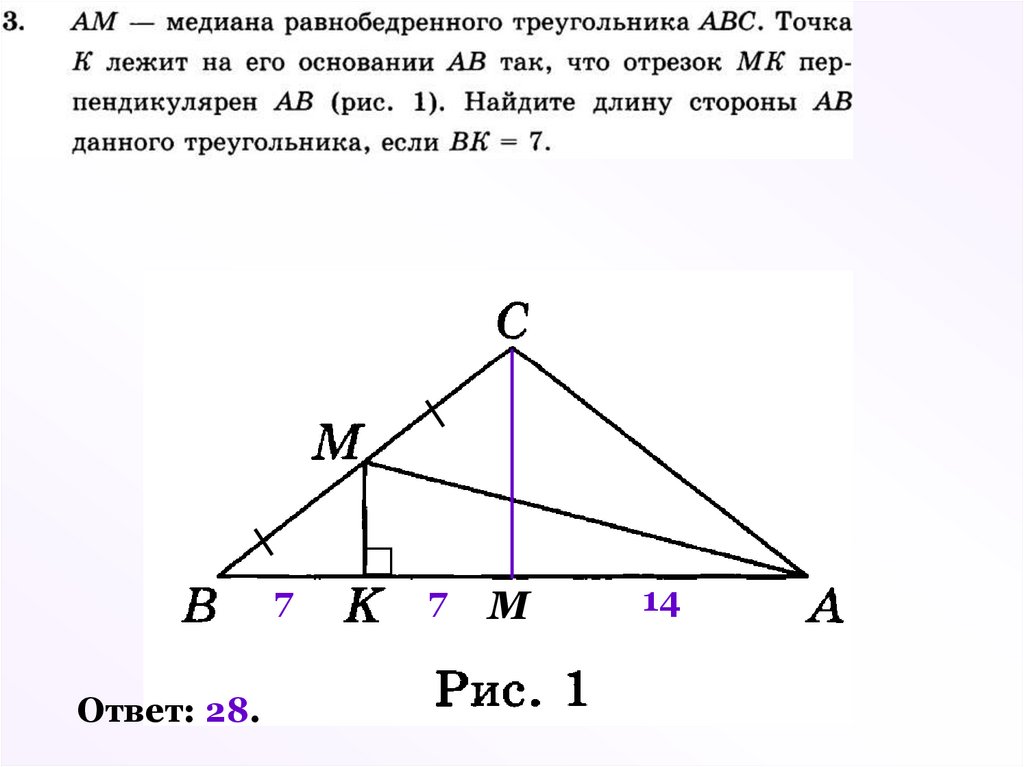
3.

7
Ответ: 28.
7
М
14

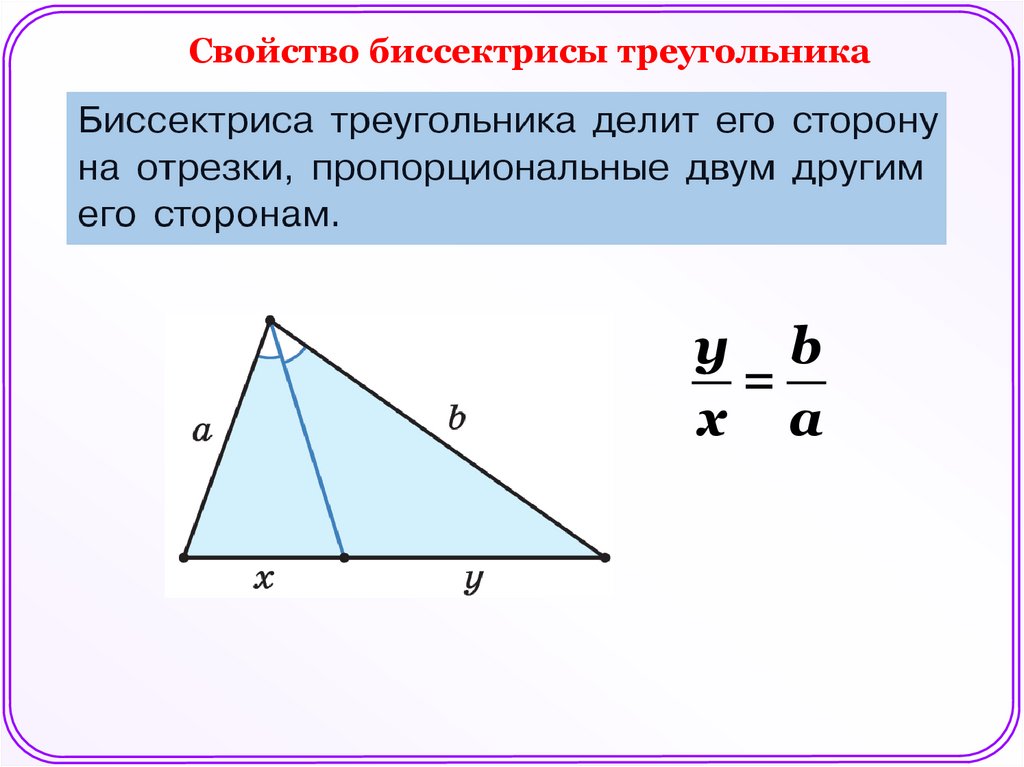
4.

Свойство биссектрисы треугольника
у b
=
x a

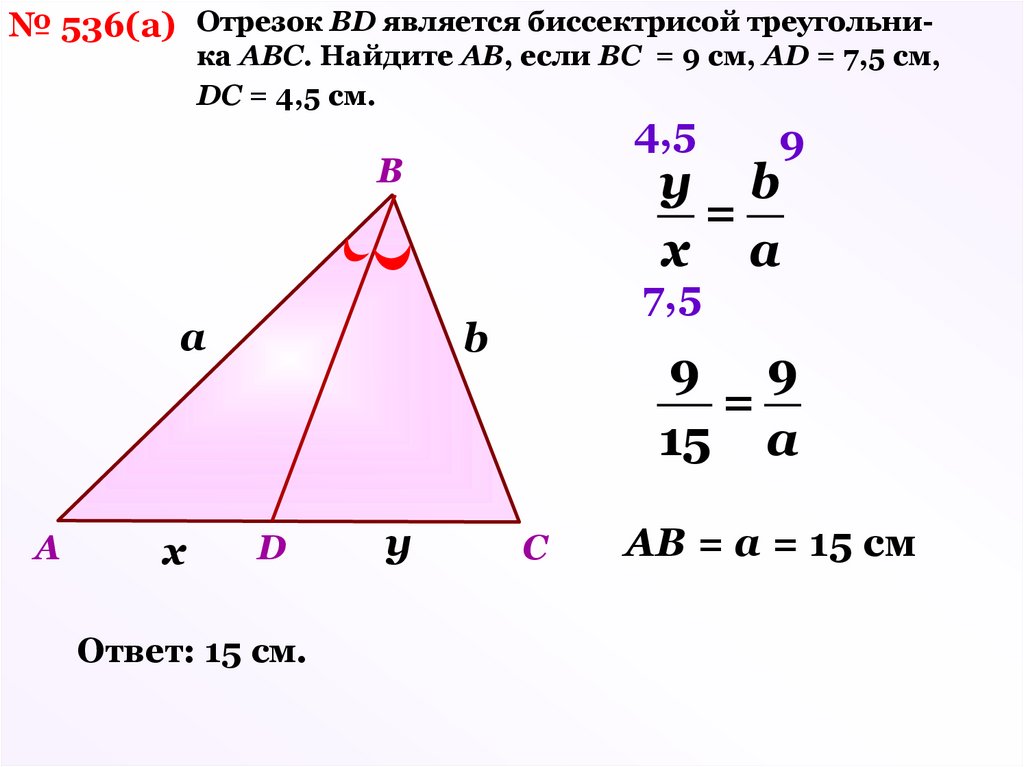
5.

№ 536(а) Oтрезок BD является биссектрисой треугольни-
ка ABC. Hайдите AB, если ВС = 9 см, AD = 7,5 см,
DC = 4,5 см.
4,5
B
а
A
х
у b
=
x a
7,5
b
D
Ответ: 15 см.
у
9
9 9
=
15 a
C
АВ = а = 15 см

6.

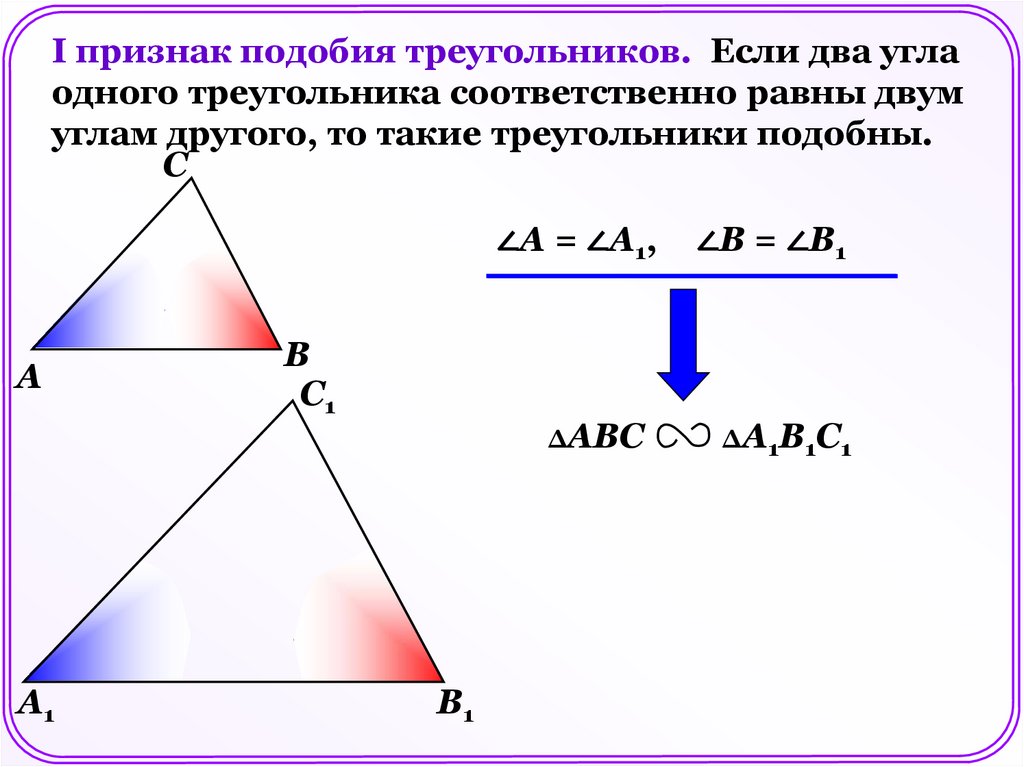
I признак подобия треугольников. Если два угла
одного треугольника соответственно равны двум
углам другого, то такие треугольники подобны.
С
А
А1
В
С1
В1
∠А = ∠А1,
∠В = ∠В1
ΔАВС
ΔА1В1С1

7.

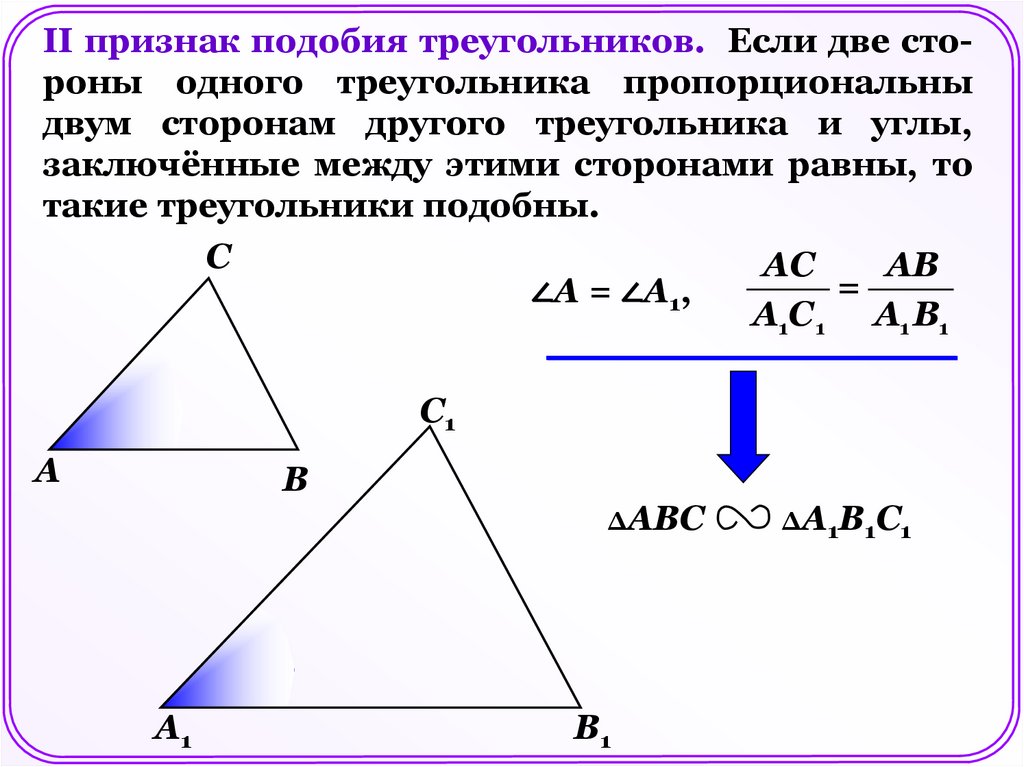
II признак подобия треугольников. Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы,
заключённые между этими сторонами равны, то
такие треугольники подобны.
С
АС
АВ
=
∠А = ∠А1,
А1С 1 A1 В1
С1
А
В
ΔАВС
А1
В1
ΔА1В1С1

8.

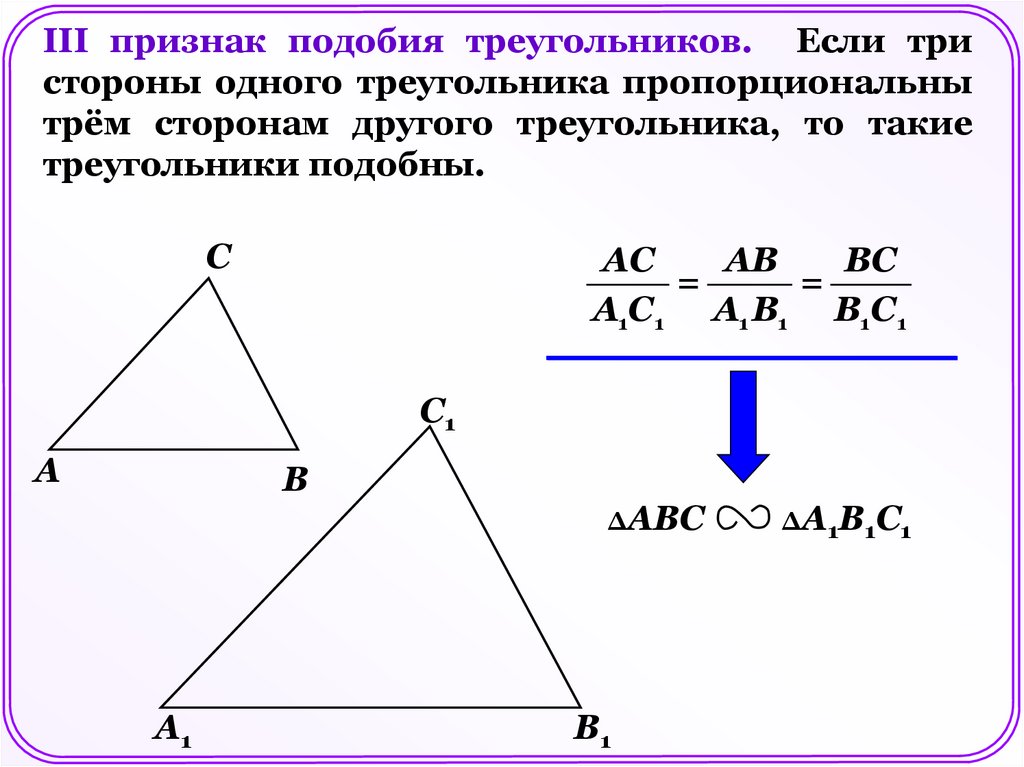
III признак подобия треугольников. Если три
стороны одного треугольника пропорциональны
трём сторонам другого треугольника, то такие
треугольники подобны.
С
АС
АВ
ВС
=
=
А1С1 A1 В1 В1С1
С1
А
В
ΔАВС
А1
В1
ΔА1В1С1

9.

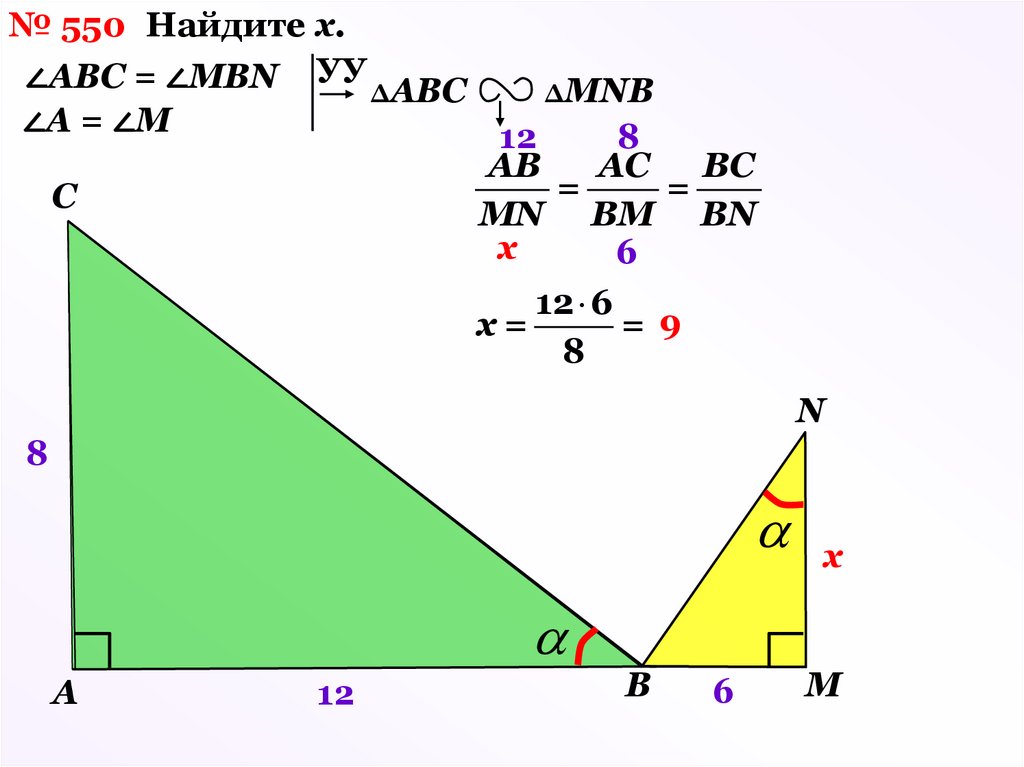
№ 550 Найдите х.
∠АВС = ∠МВN УУ ΔАВС
ΔМNВ
∠А = ∠М
12
8
АВ
АС
ВС
=
=
С
MN ВM BN
х
6
12 6
х=
= 9
8
N
8
х
A
12
В
6
М

10.

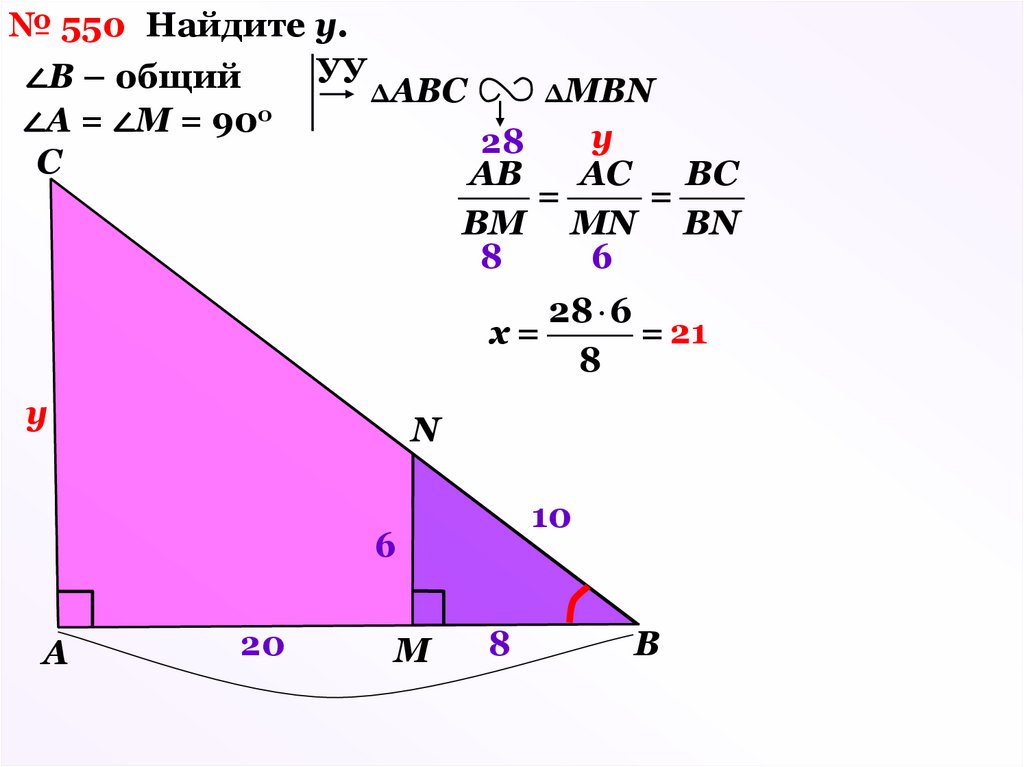
№ 550 Найдите у.
УУ
∠В – общий
ΔАВС
ΔМВN
о
∠А = ∠М = 90
у
28
С
АВ
АС
ВС
=
=
ВM MN BN
8
6
28 6
х=
= 21
8
у
N
10
6
А
20
М
8
В

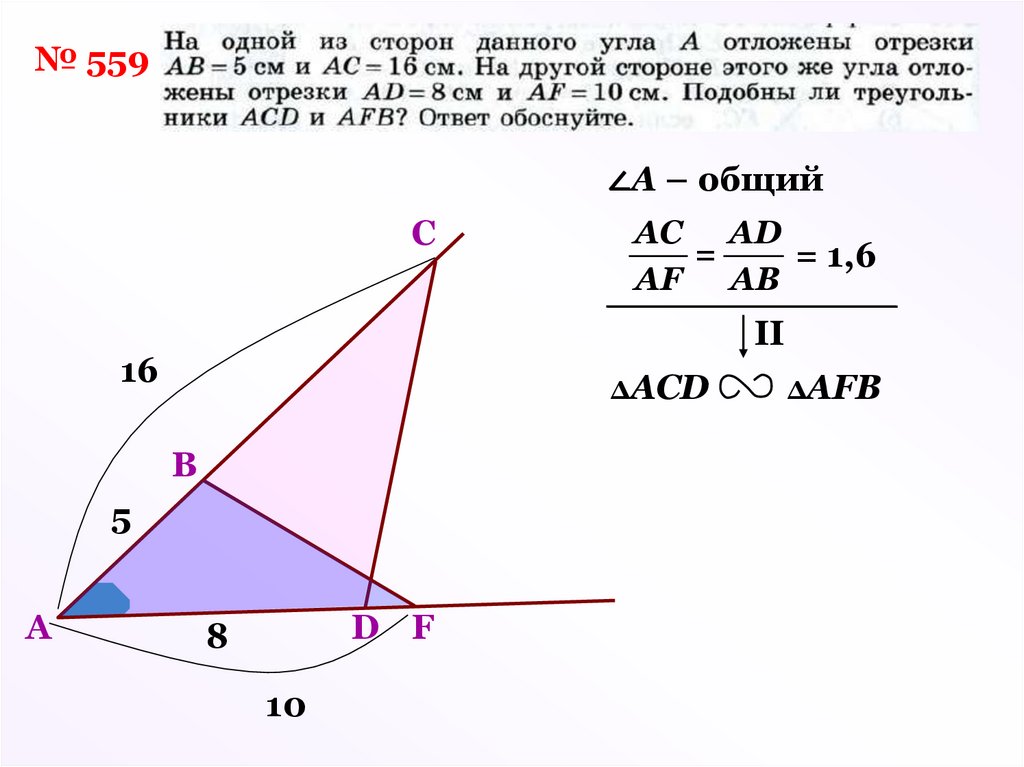
11.

№ 559
∠А – общий
C
II
16
ΔАСD
B
5
A
АС АD
=
= 1,6
AF AB
D F
8
10
ΔАFВ

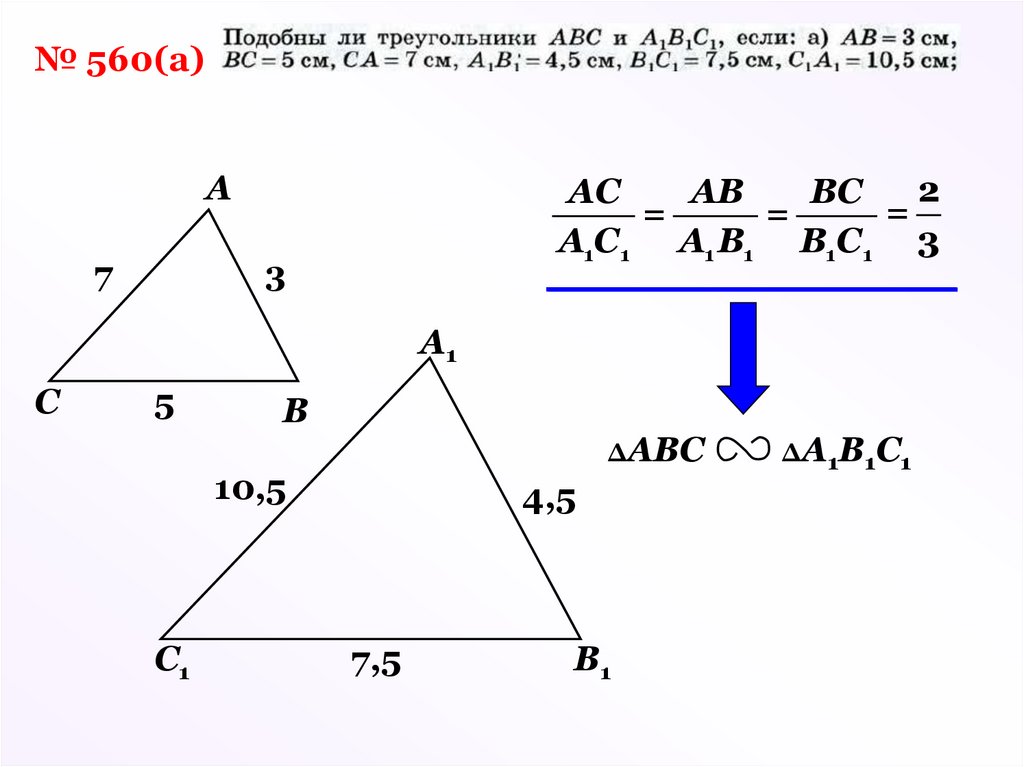
12.

№ 560(а)
А
7
2
АС
АВ
ВС
=
=
=
А1С1 A1 В1 В1С1 3
3
А1
С
5
В
ΔАВС
10,5
С1
4,5
7,5
В1
ΔА1В1С1

13.

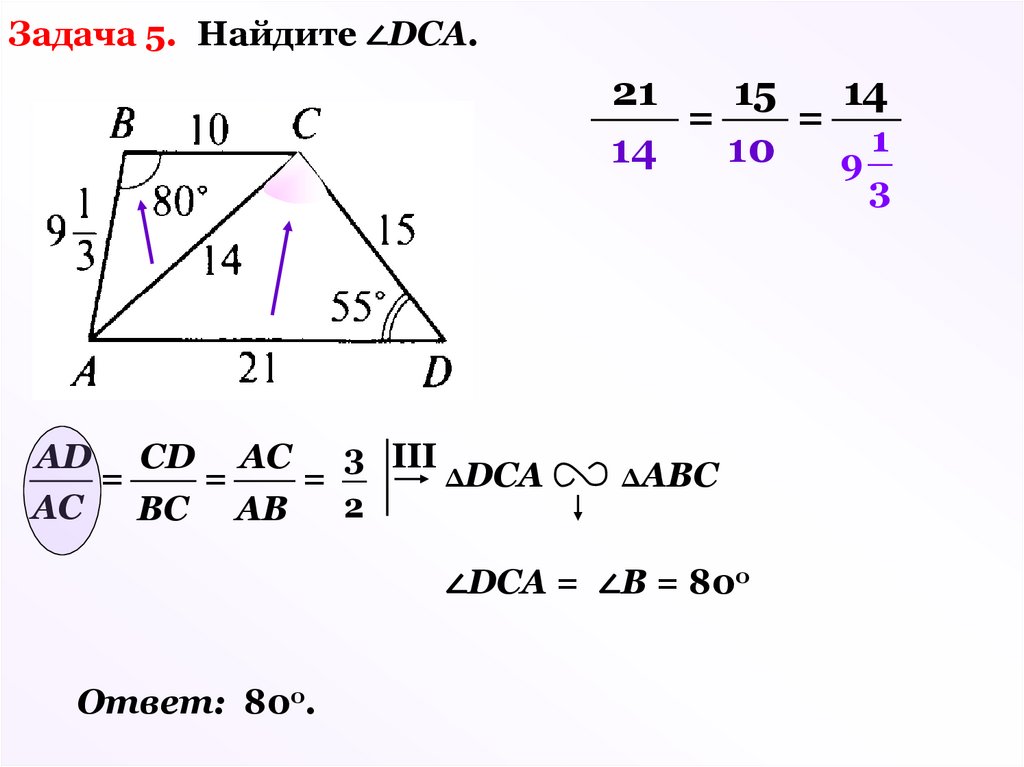
Задача 5. Найдите ∠DCA.
21
15
14
=
=
1
10
14
9
3
AD CD АС
3 III
ΔDCА
=
=
=
2
АС
ВС АВ
ΔАВС
∠DCA = ∠В = 80о
Ответ: 80о.

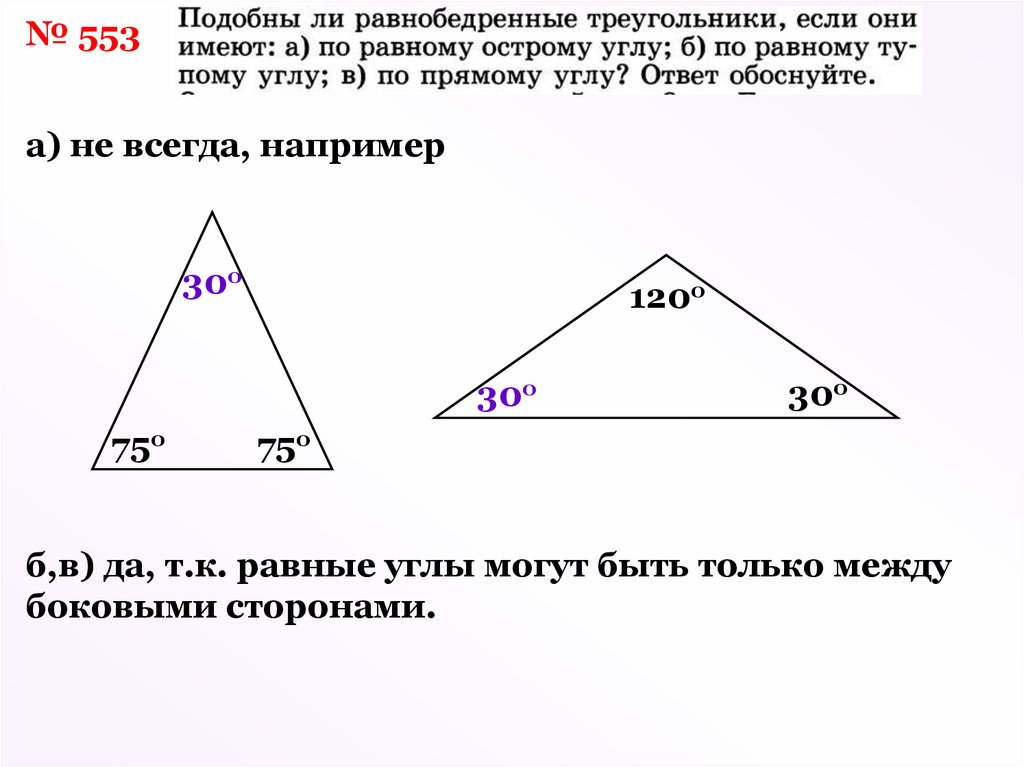
14.

№ 553
а) не всегда, например
30о
120о
30о
75о
30о
75о
б,в) да, т.к. равные углы могут быть только между
боковыми сторонами.

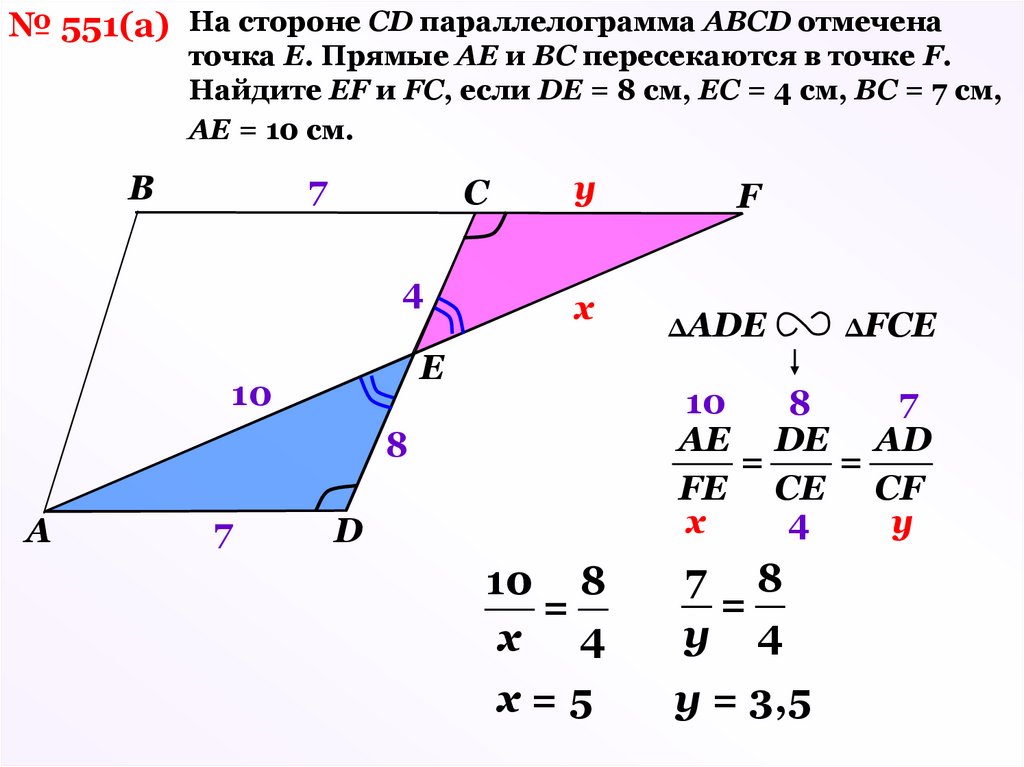
15.

№ 551(а) Hа стороне CD параллелограмма ABCD отмечена
точка Е. Прямые AE и BC пересекаются в точке F.
Hайдите EF и FC, если DE = 8 см, ЕC = 4 см, BC = 7 см,
AE = 10 см.
В
7
С
4
у
х
Е
10
7
ΔАDЕ
ΔFCE
7
10
8
АЕ DE AD
=
=
FE CE CF
х
4
у
8
А
F
D
10 8
=
х 4
7 8
=
у 4
х=5
у = 3,5

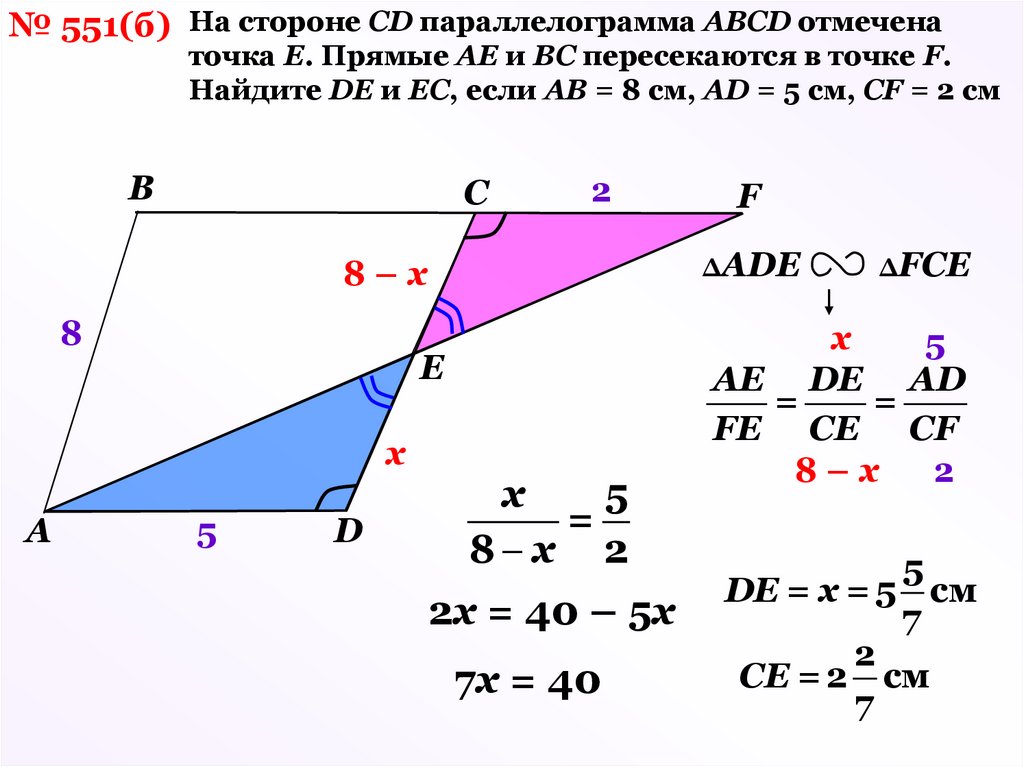
16.

№ 551(б) Hа стороне CD параллелограмма ABCD отмечена
точка Е. Прямые AE и BC пересекаются в точке F.
Hайдите DE и ЕC, если AB = 8 см, AD = 5 см, CF = 2 см
В
С
2
ΔАDЕ
8–х
8
Е
х
А
5
D
F
х
5
=
8 х 2
2х = 40 – 5х
7х = 40
ΔFCE
х
5
АЕ DE AD
=
=
FE CE CF
8–х
2
5
DE = х = 5 см
7
2
СE = 2 см
7

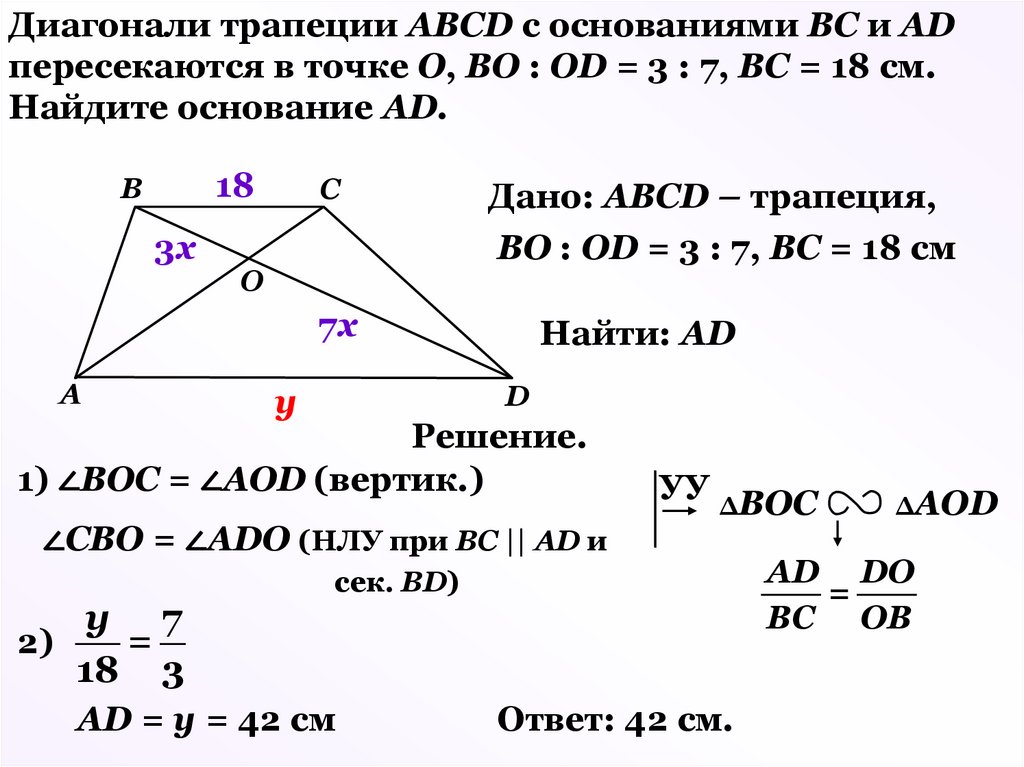
17.

Диагонали трапеции АВСD с основаниями ВС и АD
пересекаются в точке О, ВО : ОD = 3 : 7, ВС = 18 см.
Найдите основание АD.
18
В
3х
С
О
Дано: АВСD – трапеция,
ВО : ОD = 3 : 7, ВС = 18 см
7х
А
Найти: АD
D
у
Решение.
1) ∠ВОС = ∠АОD (вертик.)
∠СВО = ∠АDО (НЛУ при ВС || АD и
у 7
=
2)
18 3
УУ ΔВОС
сек. ВD)
АD = у = 42 см
Ответ: 42 см.
ΔАОD
АD DO
=
ВC ОВ

18.

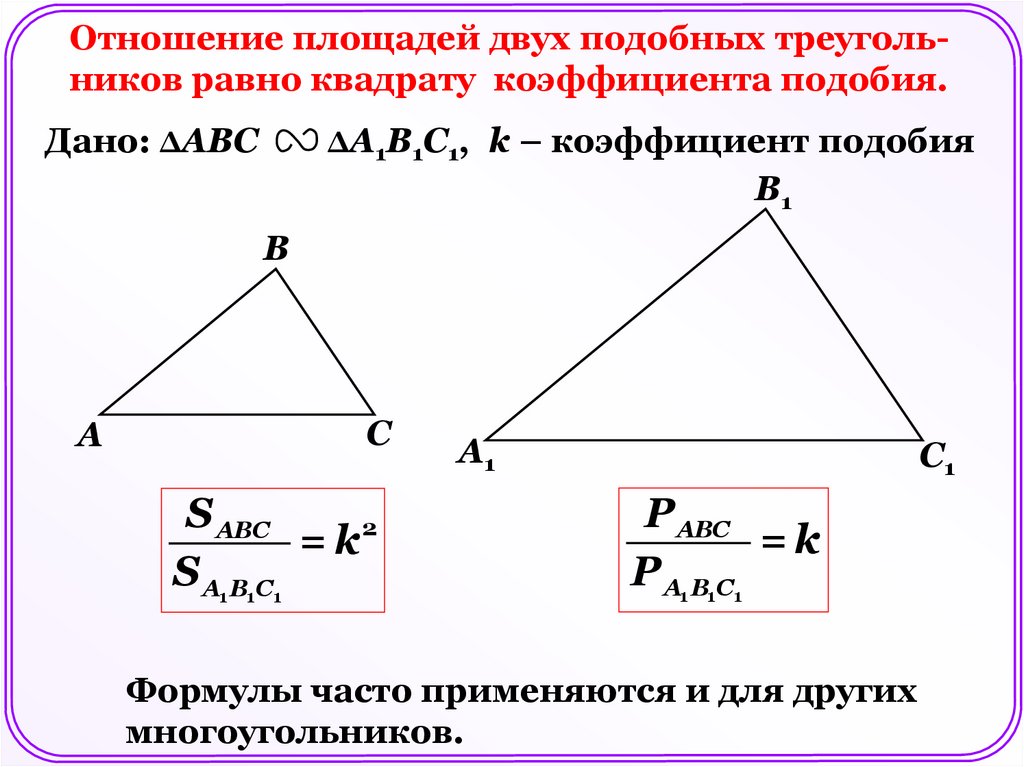
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Дано: ΔАВС
ΔА1В1С1, k – коэффициент подобия
В1
В
А
С
S АВС
= k2
S А1 В1С1
А1
С1
Р АВС
=k
Р А1 В1С1
Формулы часто применяются и для других
многоугольников.

19.

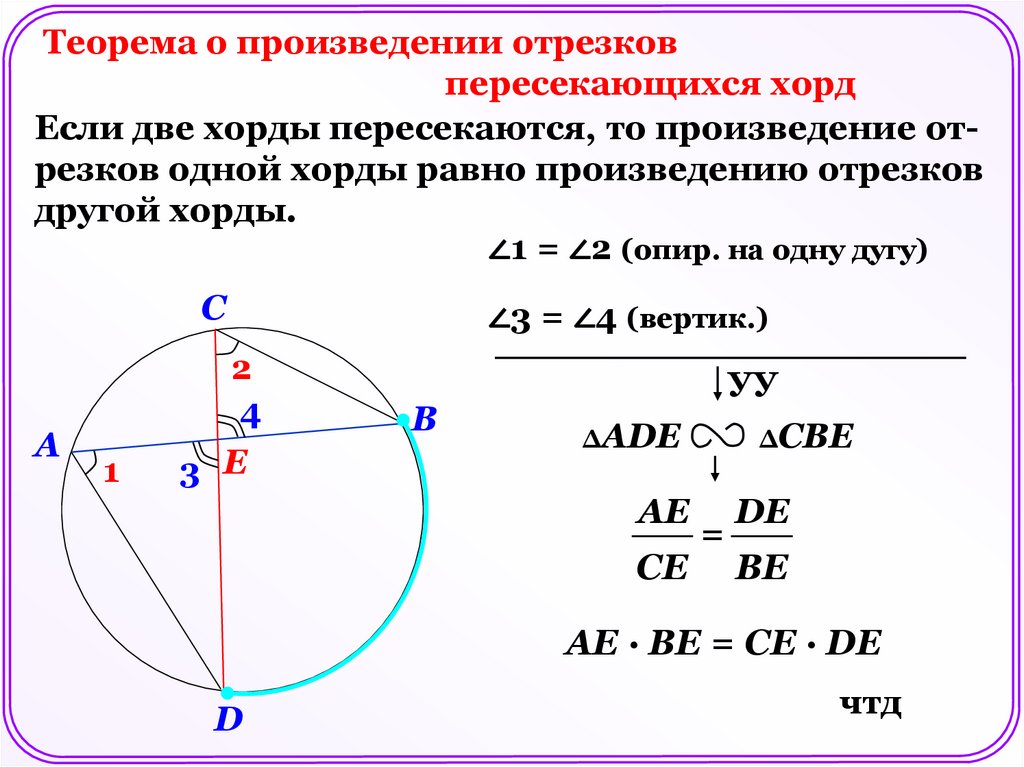
Теорема о произведении отрезков
пересекающихся хорд
Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению отрезков
другой хорды.
∠1 = ∠2 (опир. на одну дугу)
C
A
1
2
4
3 E
∠3 = ∠4 (вертик.)
B
УУ
ΔАDE
АЕ
СЕ
ΔСBE
=
DE
ВЕ
АЕ · ВЕ = СЕ · DE
D
чтд