Тригонометриялық өрнектерді теңбе-тең түрлендірудің әдіс тәсілдері

1.

«Тригонометриялық өрнектерді
теңбе-тең түрлендірудің әдіс
тәсілдері»
Орындаған: МФ-31 тобының студенті Амангельдиева А. И.
Тексерген: аға оқытушы Маутеева С. М.

2.

КІРІСПЕ
1. Тригонометриялық өрнектерді тең түрлендіру әдістерінің теориялық негіздері
1.1. Кейбір тригонометриялық функциялар
1.2. Тригонометриялық функциялардың негізгі қасиеттері
1.3. Тригонометриялық өрнектерді түрлендіру
2. Мектепте математиканы оқыту процесінде тригонометриялық өрнектерді тең түрлендіру
әдістерін қолдану бойынша әдістемелік ұсыныстар
2.1. Мектепте математиканы оқыту процесінде тригонометрия курсын меңгертудегі
жұмыстар
2.2. Тригонометриялық өрнектерді тең түрлендіру әдістерін қолдану бойынша оқушылардың
жұмысын ұйымдастыру
2.3. Тригонометриялық өрнектерді түрлендіру
ҚОРЫТЫНДЫ

3.

Тақырыптың өзектілігі: Математиканың әр қадамы өмірдің қажетінен
туады, сабақта қарастыратын көп есептер адамның практикалық дүниесіне
байланысты. Сондықтан математикалық ұғымдардың нақты және тиімді
болуы оқушылардың жеке тәрбиесіне байланысты, оқу жүйесіне қойылатын
бірінші шарт – ол оқушылардың оқу процесі өмірімен байланысты болуы.
Бұл жұмыстың негізгі мақсаты: мектептегі математика курсында
тригонометриялық өрнектерді тең түрлендіру әдістерін зерттеу және жүйелеу,
сонымен қатар оқытушыларға әдістемелік ұсыныстарды ұсыну.
Зерттеу міндеттері:
• Тригонометриялық өрнектердің тең түрленуінің теориялық негіздерін
зерттеу;
• Осы тақырыпты оқытудың қолданыстағы әдістемелік тәсілдерін талдау;
• Өзіңіздің әдістемелік ұсыныстарыңызды әзірлеу және сынақтан өткізу;
• Тәжірибеде ұсынылған тәсілдердің тиімділігін бағалау.

4.

Зерттеу болжамы: жұмыс нәтижелері мектептерде тригонометрияны оқыту
сапасын жақсартады деп күтілуде, бұл материалды оқушылар үшін қол жетімді және
қызықты етеді.
Зерттеудің маңыздылығы: жұмыс оқушылардың тригонометриялық материалды
тереңірек және сапалы игеруін қамтамасыз ете отырып, Орта мектептегі оқу
процесінің тиімділігін арттыруға ықпал етеді.
Зерттеу пәні: тригонометриялық өрнектерді тең түрлендіру әдістері.
Зерттеу нысаны: орта мектепте математиканы оқыту процесі.
Зерттеу әдістері: жұмыста теориялық талдау, салыстыру, жалпылау әдістері,
сондай-ақ әзірленген әдістемелік ұсыныстарды сынақтан өткізу үшін педагогикалық
эксперимент әдістері қолданылады.

5.

Тригонометрия (грек. trіgōnon – үшбұрыш және metreo – өлшеу) – геометрияның үшбұрыш
элементтерінің арасындағы метрикалық қатыс тригонометриялық функциялар арқылы
өрнектелетін саласы.
Тригонометрия сөзі алғаш рет 1505 жылы неміс геологы және математигі Питискустың
кітабының мазмұнында кездеседі. «Тригонометрия» атауының өзі грек сөзінен аударғанда
«үшбұрыштарды өлшеу» деген ұғымды білдіреді.

6.

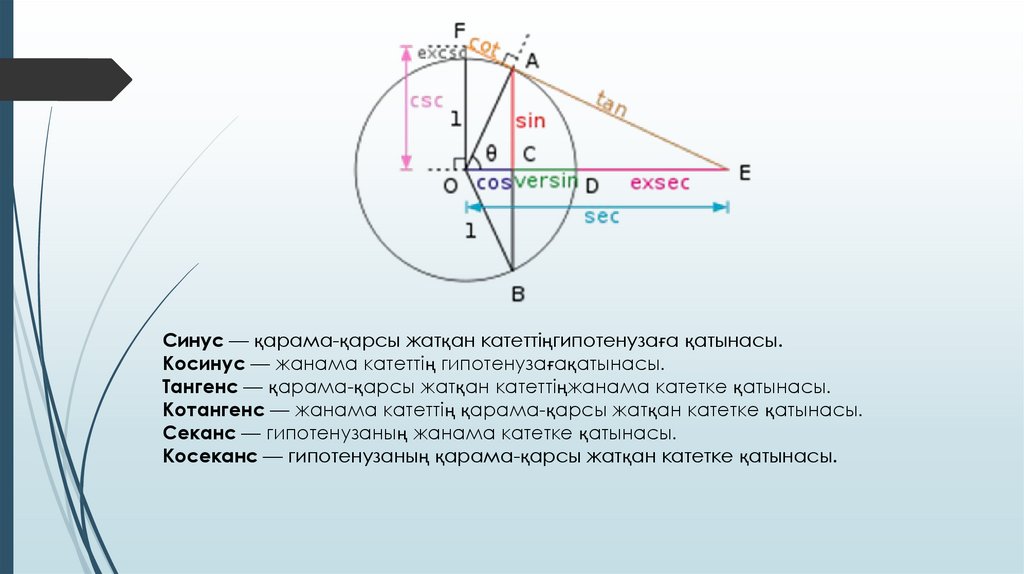
Синус — қарама-қарсы жатқан катеттіңгипотенузаға қатынасы.
Косинус — жанама катеттің гипотенузағақатынасы.
Тангенс — қарама-қарсы жатқан катеттіңжанама катетке қатынасы.
Котангенс — жанама катеттің қарама-қарсы жатқан катетке қатынасы.
Секанс — гипотенузаның жанама катетке қатынасы.
Косеканс — гипотенузаның қарама-қарсы жатқан катетке қатынасы.

7.

МЫСАЛ: А-деңгейдегі
Оқу үрдісінің бастапқы кезеңінде оқушыларға бірден қиын есептерді беру қателік
деп санаймын. Жаңа мәліметтерді түсіндіру бірінші А-деңгейдегі (яғни жеңілдетілген)
есептерді беру қажет.
Мысалы:
1+2