Степень с натуральным показателем

1. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

2. Определение степени с натуральным показателем

3. Проверь себя

Заполните пропуски лабиринта, учитывая, что
преобразования ведутся в направлении, указанном
стрелкой
Cвой
пример

4.

Связь понятия степени с
другими понятиями
математики
1
•Числовые множества
2
•Буквенные
выражения
3
•Функция

5.

Определение
Функцию вида
называют степенной функцией
с натуральным показателем

6.

y x
2
y
График функции –
у x2
парабола
-1
0 1
x
у x2

7.

y x
3
График функции кубическая парабола
y
у x3
1
0 1
x
у x3
ветви кубической
параболы

8. Степенная функция, ее графики и свойства.

9.

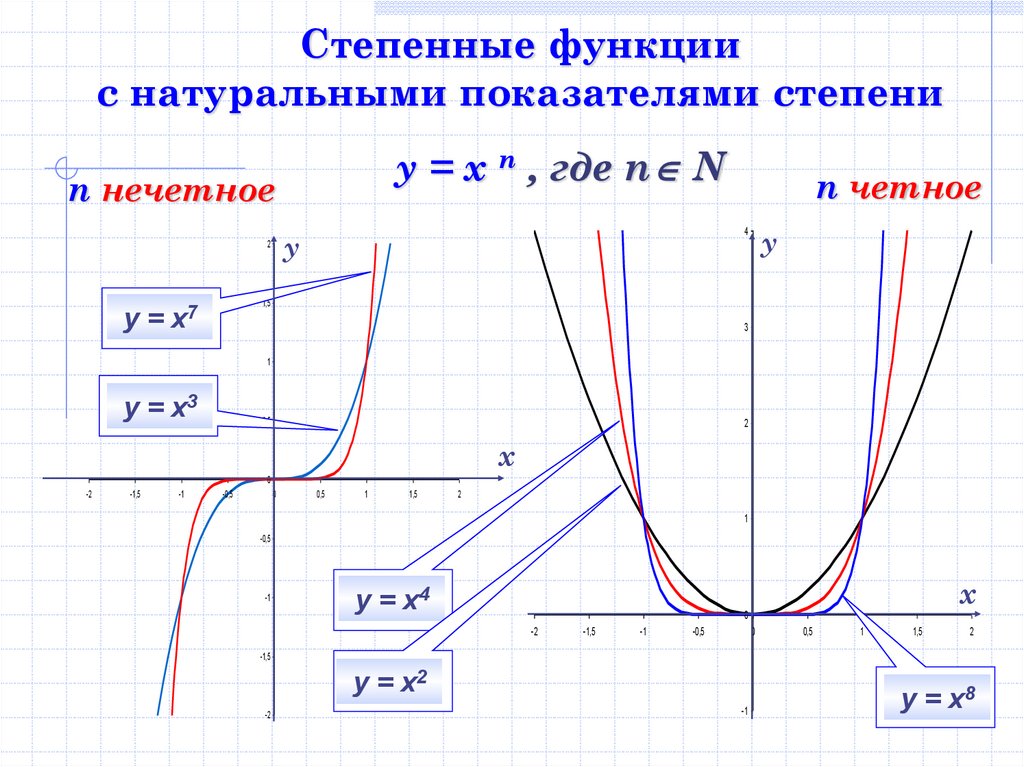
Степенные функции
с натуральными показателями степени
у = х n , где n N
n нечетное
у
4
у
2
n четное
1,5
у = х7
3
1
у = х3
0,5
2
х
0
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
1
-0,5
-1
у = х4
х
0
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
-1,5
у = х2
-2
-1
у = х8

10.

Свойства степенных функций
с натуральными показателями степени
у = х n , где n N
n четное
Область определения : (- ∞; + ∞)
у
4
Область значений: [0; + ∞)
Противоположным значениям
аргумента соответствуют
равные значения функции:
у(-х) = у(х), четная
Промежутки знакопостоянства:
3
2
у > 0 на (- ∞; 0) (0; + ∞)
Возрастание (убывание):
убывает на (- ∞; 0]
1
х
0
-2
-1,5
-1
-0,5
0
-1
0,5
1
1,5
возрастает на [0; + ∞)
Особые точки:
2
(-1; 1), (0; 0), (1; 1)

11.

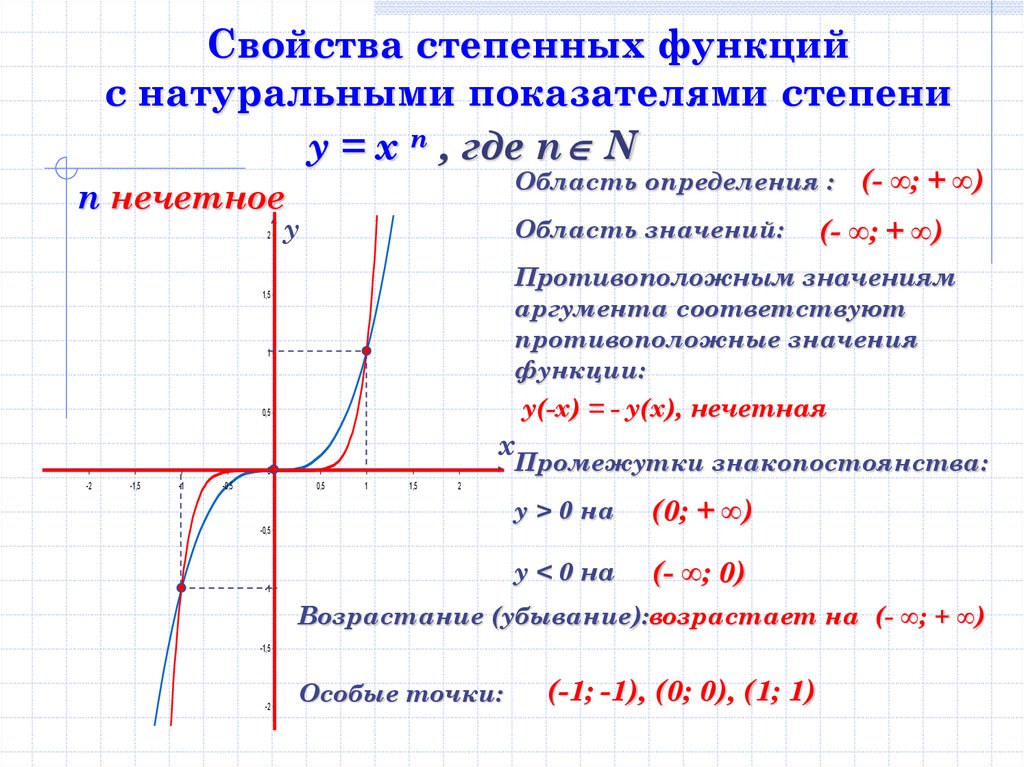
Свойства степенных функций
с натуральными показателями степени
у = х n , где n N
Область определения :
n нечетное
у
2
Область значений:
(- ∞; + ∞)
(- ∞; + ∞)
Противоположным значениям
аргумента соответствуют
противоположные значения
функции:
у(-х) = - у(х), нечетная
1,5
1
0,5
х
Промежутки знакопостоянства:
0
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
у > 0 на
(0; + ∞)
у < 0 на
(- ∞; 0)
-0,5
-1
Возрастание (убывание):возрастает на (- ∞; + ∞)
-1,5
-2
Особые точки:
(-1; -1), (0; 0), (1; 1)

12. Домашнее задание:

п.8 (выучить теоретический материал) по
опорному конспекту;
№136,141,150(а),
повт.156 (б)(это пример из экзамена)