Тангенс и котангенс

1.

Математика
Преподаватели:
Мовсисян Геворг Суренович,
Попова Ольга Николаевна

2.

Тема 6.
Тангенс и
Котангенс

3.

План лекции
Введение.
1. Определение тангенса и
котангенса.
2. Свойства тангенса и
котангенса.
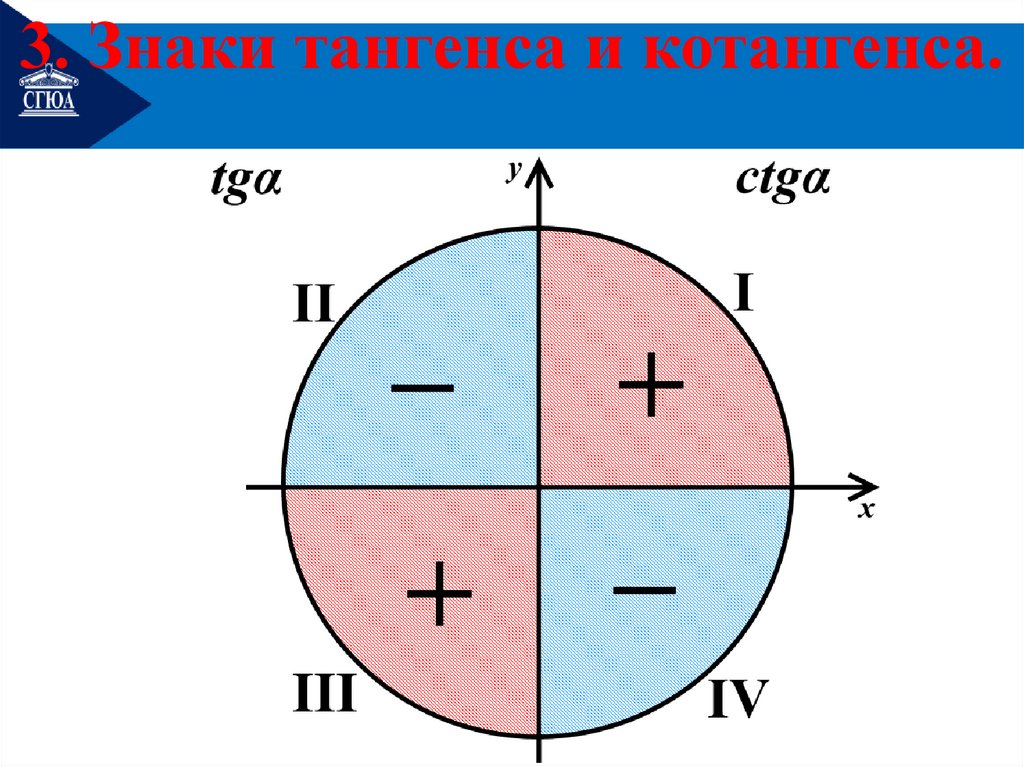
3. Знаки тангенса и котангенса.
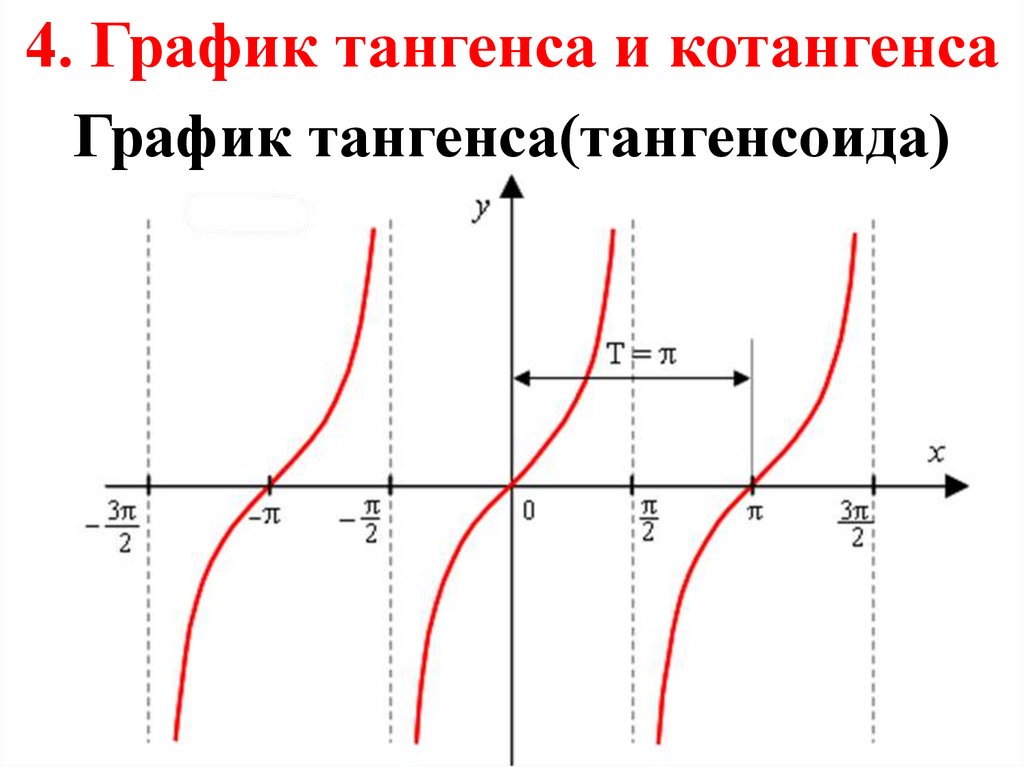
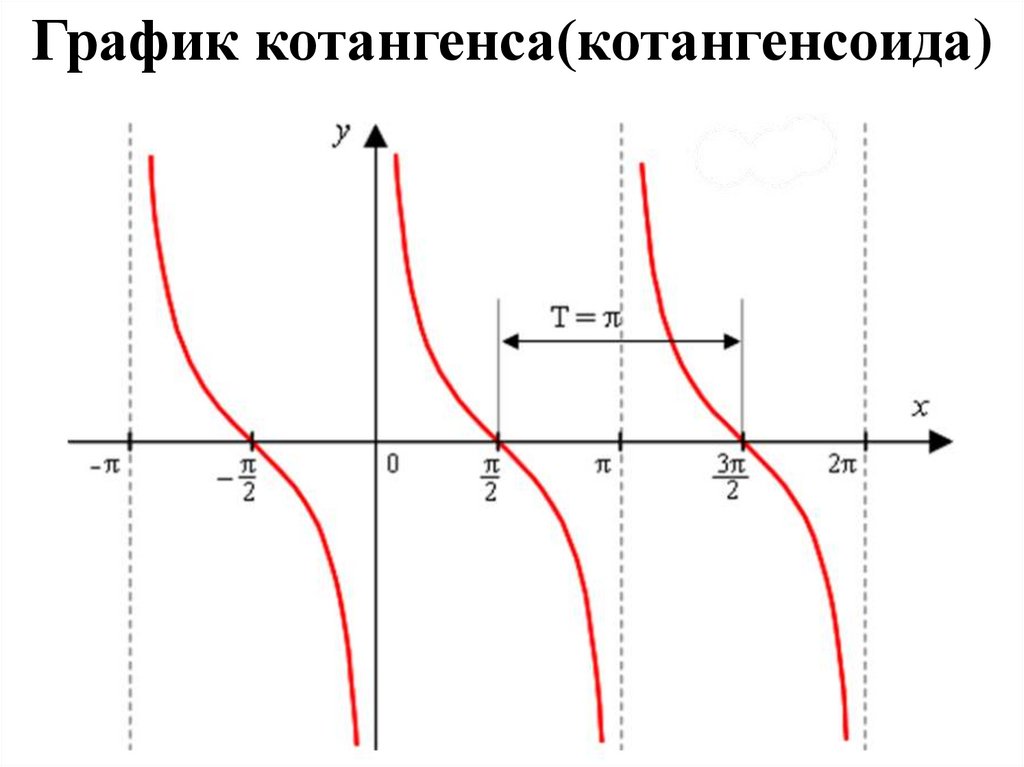
4. Графики тангенса и
котангенса.

4.

Введение
Название «тангенс» ,
происходящее от латинского
tanger (касаться), появилось в
1583 г.. Tangens переводится
как «касающийся». Дело в
том, что линия тангенсов –
касательная к единичной
окружности.

5.

Тангенс (а так же котангенс)
обязан своему появлению
арабскому математику,
астроному Абу-ль-Вафе в X веке.
Он же составил первые таблицы
для нахождения значений
тангенсов и котангенсов.

6.

Однако эти открытия долгое
время оставались
неизвестными европейским
ученым, и тангенсы были
заново открыты лишь в XIV
веке немецким математиком,
астрономом Регимонтаном.

7.

Региомонтан составил
подробные
тригонометрические таблицы.
Благодаря его трудам плоская
и сферическая тригонометрия
стала самостоятельной
дисциплиной и в Европе.

8.

1.Определение тангенса и
котангенса.
Напомним, что мы находимся
в тригонометрическом круге,
т.е в единичной числовой
окружности.
Так же напомним, что
sin y, cos x

9.

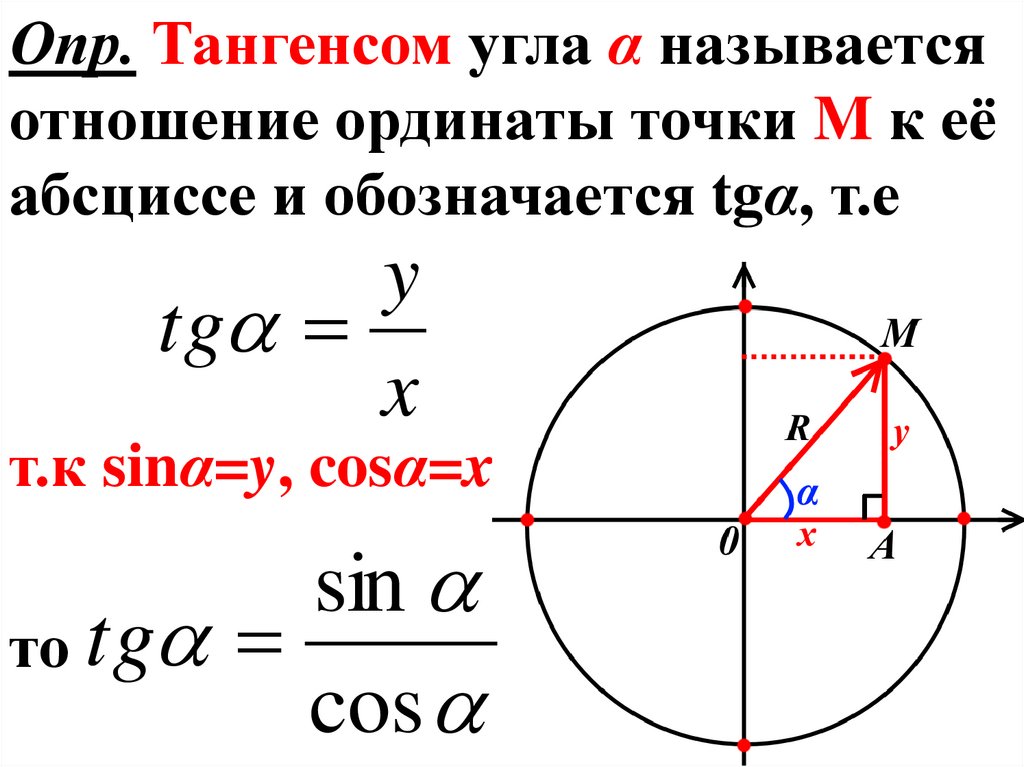
Опр. Тангенсом угла α называется
отношение ординаты точки M к её
абсциссе и обозначается tgα, т.е
y
tg
x
т.к sinα=y, cosα=xб
sin
то tg
cos

10.

Линия Тангенсов
Существует наглядная и
очень полезная
геометрическая
интерпретация тангенса – с
помощью так называемой
линии тангенсов.

11.

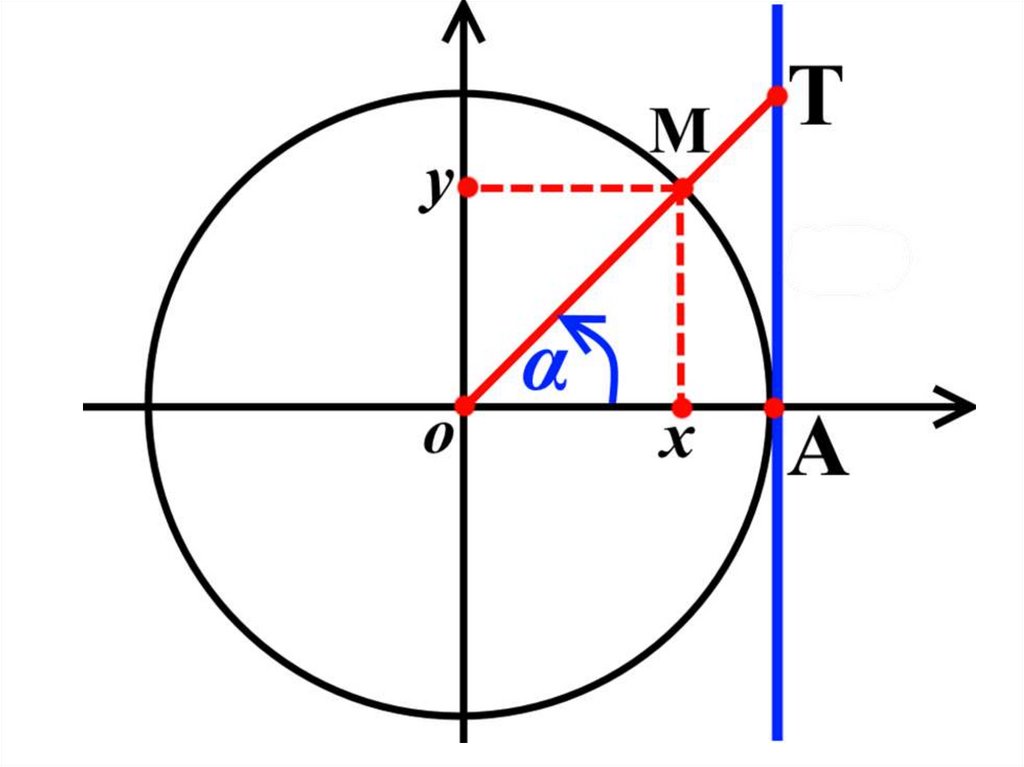
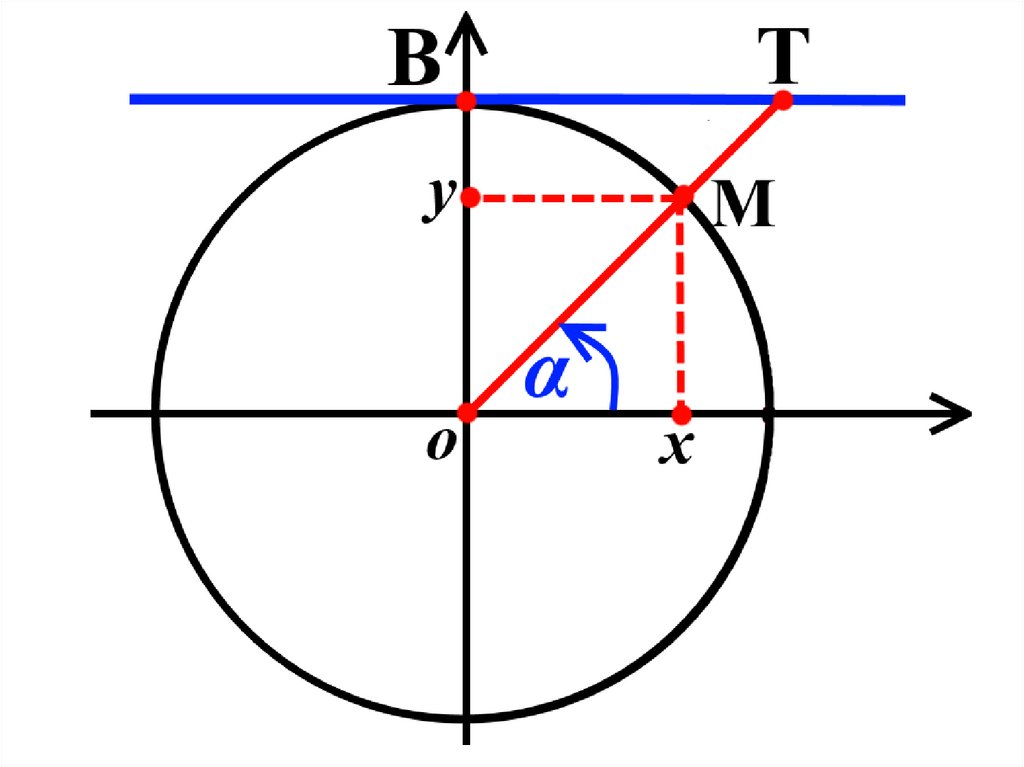
Опр. Линией тангенсов
называется касательная, к
тригонометрической
окружности, проведённая в
точке A(1; 0).
Изобразим линию тангенсов
наглядно, на рисунке.

12.

13.

Из тригонометрического
определения тангенса следует,