Вид функции в зависимости от показателя степени

1.

2.

Вид функции в зависимости от показателя степени.
у=х1/2
у=х1
у=х-2
у=х5/2
у=х2
у=х-1
у=х3
у=х1/3
у=хn/m

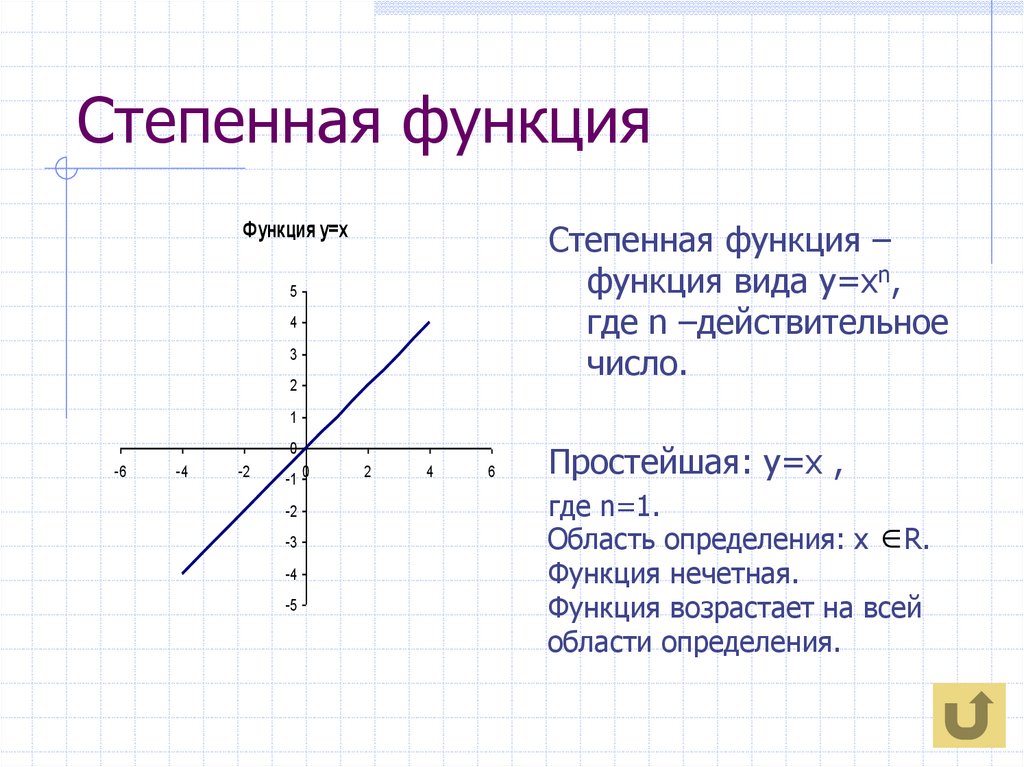
3. Степенная функция

Функция у=х
Степенная функция –
функция вида у=хn,
где n –действительное
число.
5
4
3
2
1
0
-6
-4
-2
-1 0
-2
-3
-4
-5
2
4
6
Простейшая: у=х ,
где n=1.
Область определения: х R.
Функция нечетная.
Функция возрастает на всей
области определения.

4. Степенная функция с натуральным показателем степени.

n - четный
2
Функция у=х
Область определения: х R.
Функция четная.
Функция убывает при х (- ;0].
Функция возрастает
при х [0;=+ ).
10
8
6
4
2
0
-4
-3
-2
-1
0
1
2
3
4

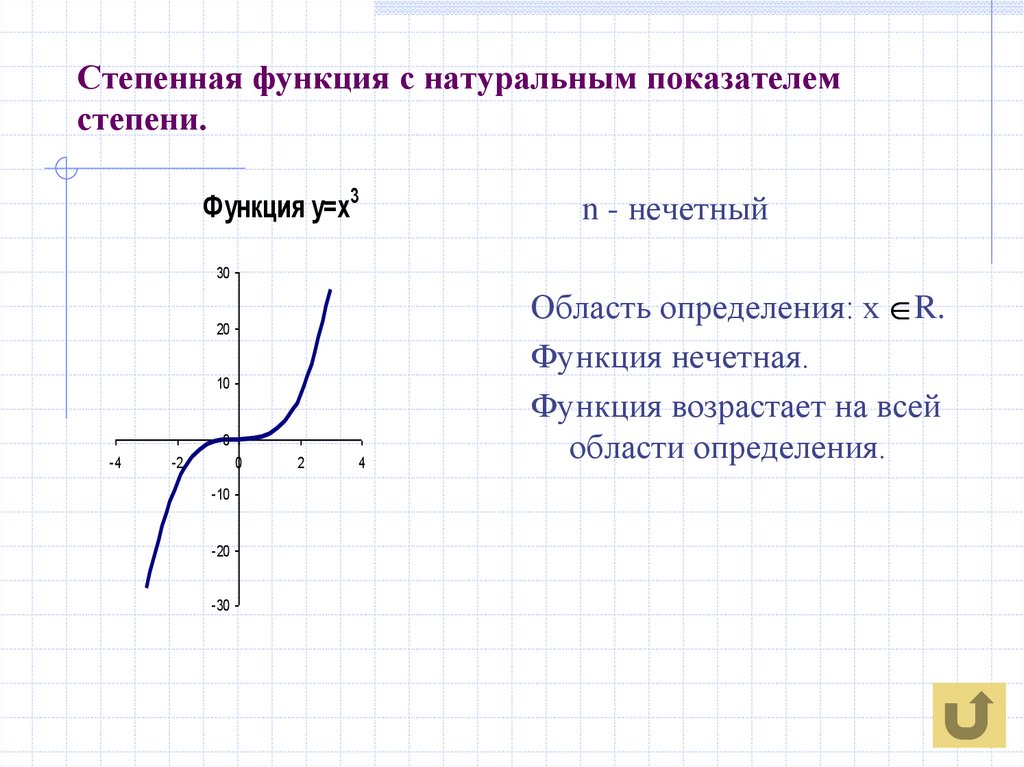
5. Степенная функция с натуральным показателем степени.

Функция у=х3
n - нечетный
30
20
10
0
-4
-2
0
-10
-20
-30
2
4
Область определения: х R.
Функция нечетная.
Функция возрастает на всей
области определения.

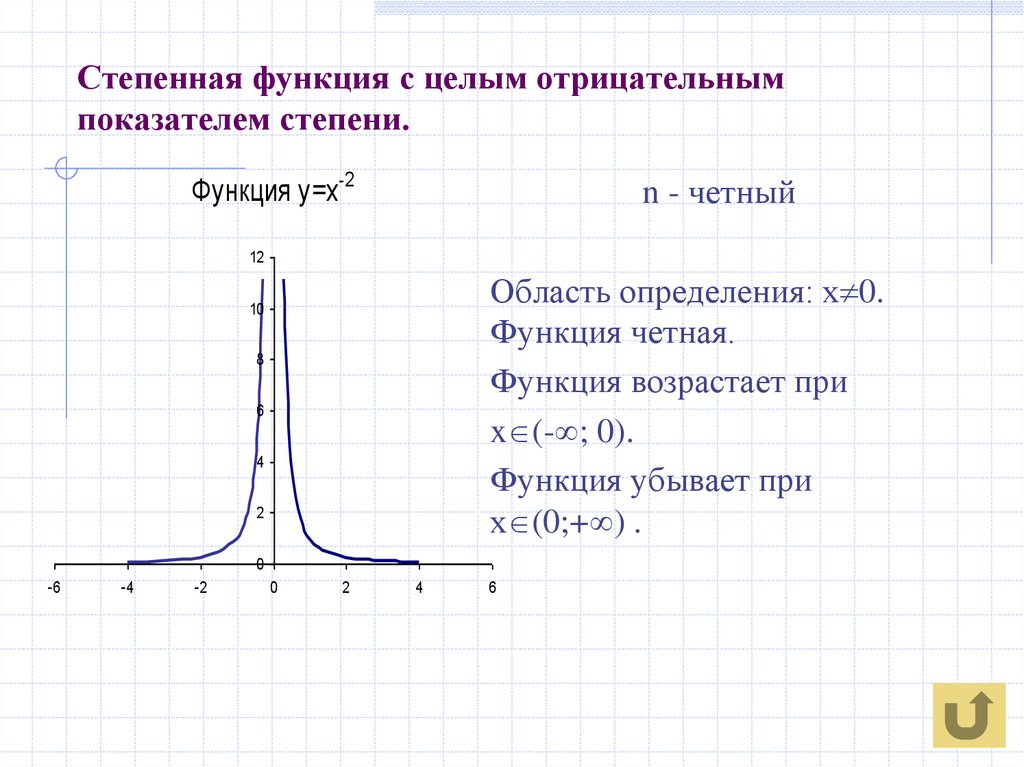
6. Степенная функция с целым отрицательным показателем степени.

Функция у=х-2
n - четный
12
Область определения: х 0.
Функция четная.
Функция возрастает при
x (- ; 0).
Функция убывает при
х (0;+ ) .
10
8
6
4
2
0
-6
-4
-2
0
2
4
6

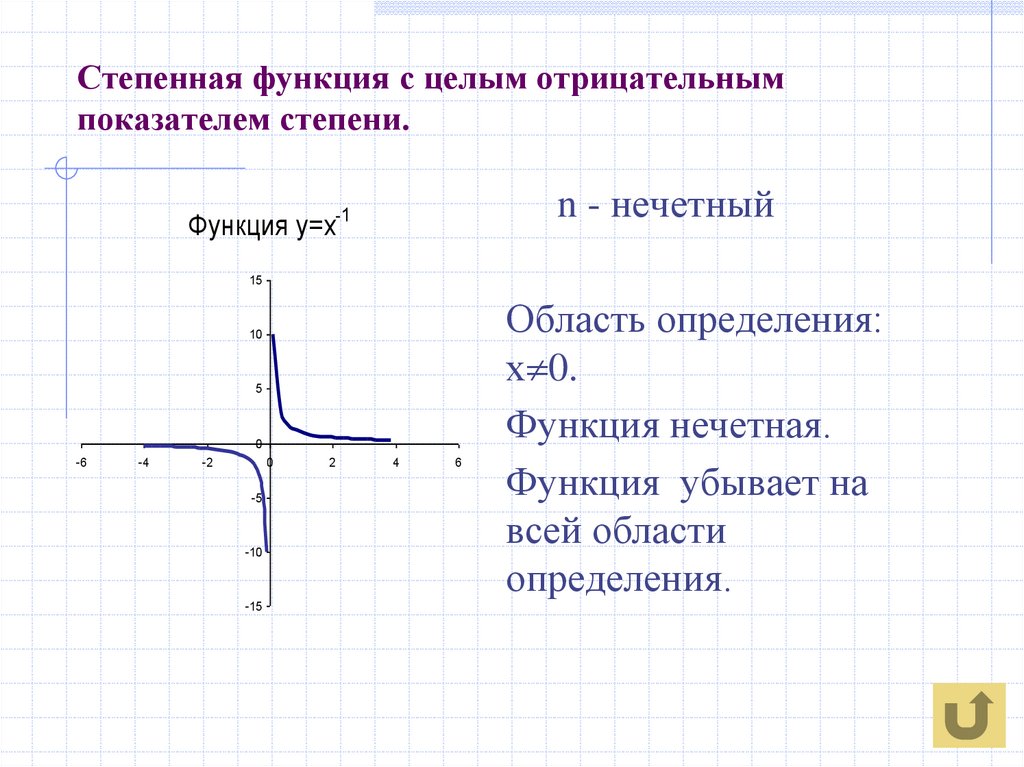
7. Степенная функция с целым отрицательным показателем степени.

n - нечетный
Функция у=х-1
15
10
5
0
-6
-4
0
-2
-5
-10
-15
2
4
6
Область определения:
х 0.
Функция нечетная.
Функция убывает на
всей области
определения.

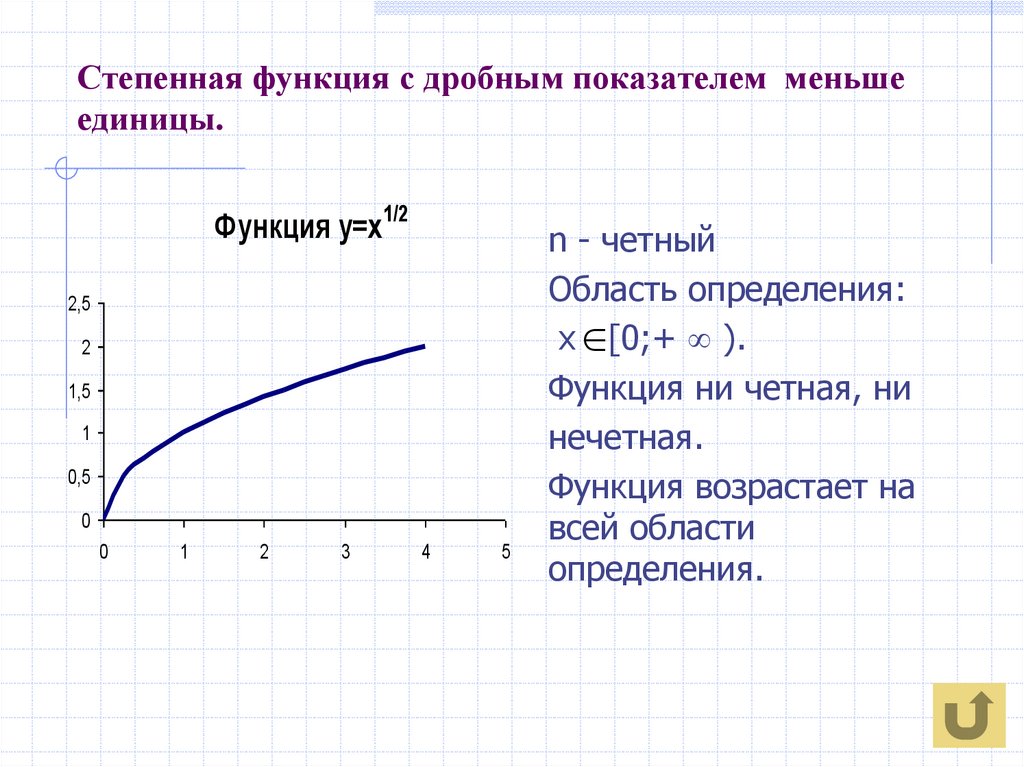
8. Степенная функция с дробным показателем меньше единицы.

Функция у=х1/2
2,5
2
1,5
1
0,5
0
0
1
2
3
4
5
n - четный
Область определения:
х [0;+ ).
Функция ни четная, ни
нечетная.
Функция возрастает на
всей области
определения.

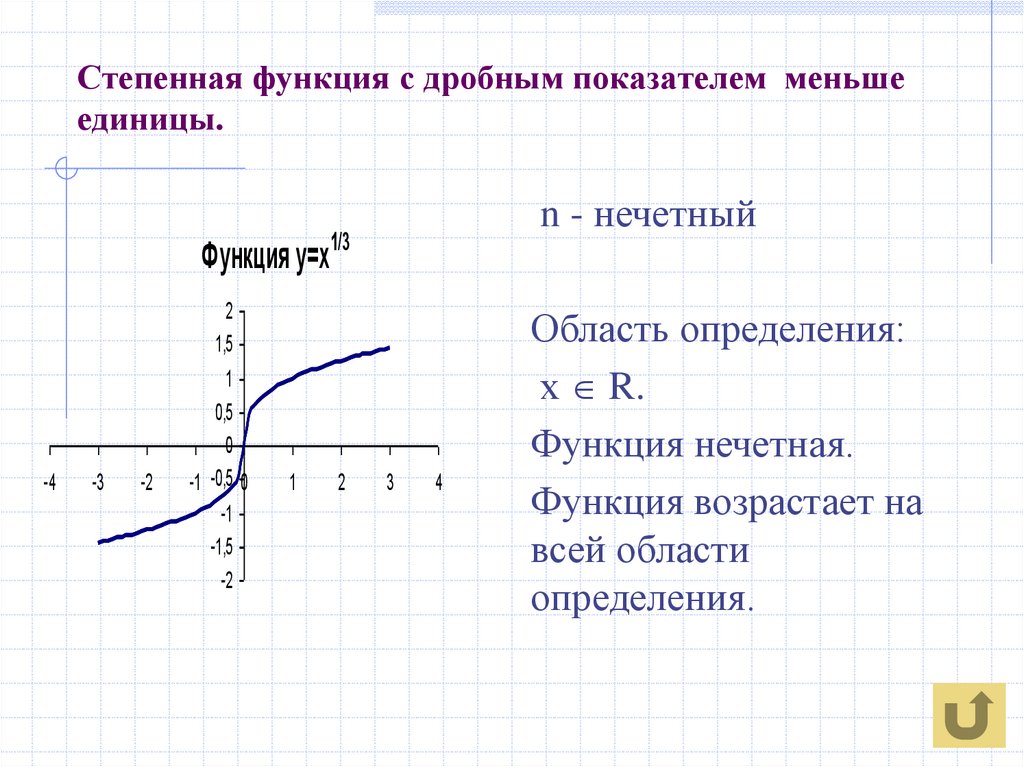
9. Степенная функция с дробным показателем меньше единицы.

n - нечетный
Функция у=х1/3
-4
-3
-2
2
1,5
1
0,5
0
-1 -0,5 0
-1
-1,5
-2
1
2
3
4
Область определения:
х R.
Функция нечетная.
Функция возрастает на
всей области
определения.

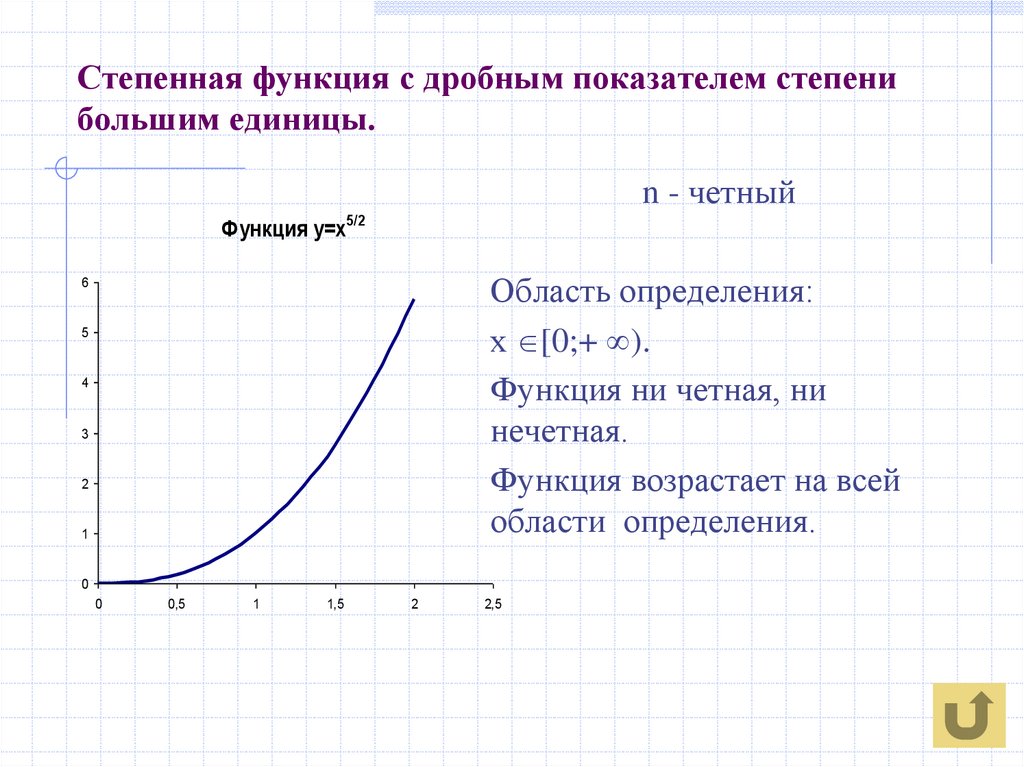
10. Степенная функция с дробным показателем степени большим единицы.

n - четный
Функция у=х5/2
Область определения:
х [0;+ ).
Функция ни четная, ни
нечетная.
Функция возрастает на всей
области определения.
6
5
4
3
2
1
0
0
0,5
1
1,5
2
2,5

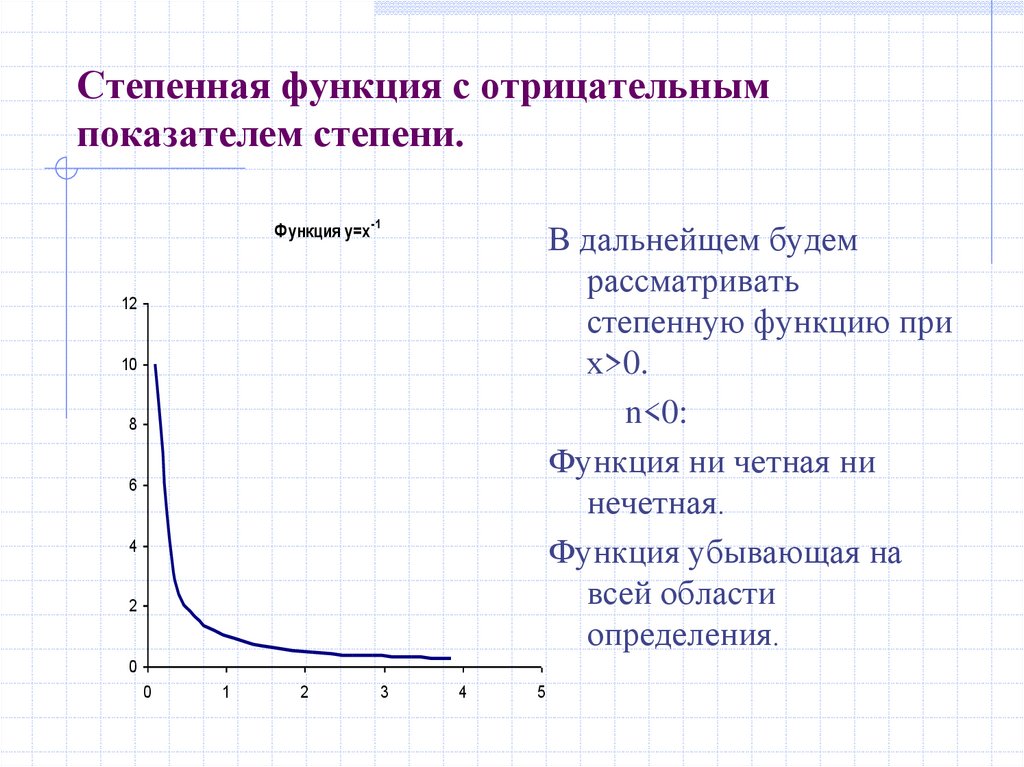
11. Степенная функция с отрицательным показателем степени.

Функция у=х
-1
В дальнейщем будем
рассматривать
степенную функцию при
х>0.
n<0:
Функция ни четная ни
нечетная.
Функция убывающая на
всей области
определения.
12
10
8
6
4
2
0
0
1
2
3
4
5

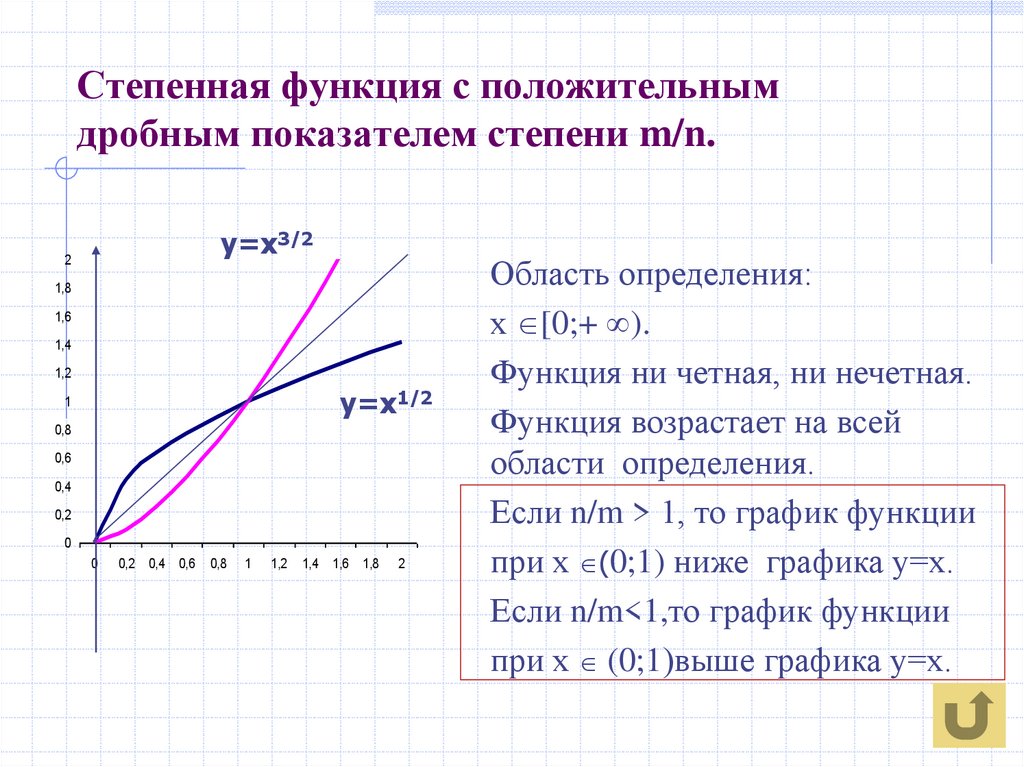
12. Степенная функция с положительным дробным показателем степени m/n.

у=х3/2
2
1,8
1,6
1,4
1,2
у=х1/2
1
0,8
0,6
0,4
0,2
0
0
0,2 0,4 0,6
0,8
1
1,2
1,4 1,6 1,8
2
Область определения:
х [0;+ ).
Функция ни четная, ни нечетная.
Функция возрастает на всей
области определения.
Если n/m > 1, то график функции
при х (0;1) ниже графика у=х.
Если n/m<1,то график функции
при х (0;1)выше графика у=х.