Степенная функция

1. Степенная функция. Учитель математики МБОУ ООШ №26 г. Энгельса Еремеева Елена Борисовна

Свойства и график степенной функции.
СТЕПЕННАЯ ФУНКЦИЯ.
УЧИТЕЛЬ МАТЕМАТИКИ МБОУ ООШ №26 Г. ЭНГЕЛЬСА
ЕРЕМЕЕВА ЕЛЕНА БОРИСОВНА

2. Функция у = хⁿ, где n = 2р (п ∈ N) – чётное натуральное число.

у
Свойства функции.
1. D (y) = R
2. E(y)= [0; +∞)
3. y(-x) = y(x) чётная
0
х
функция
4. Возрастает на[0;+∞)
убывает на (-∞;0]

3. Функция у = хⁿ, где n = 2р + 1 (п ∈ N) – нечётное натуральное число.

у
0
Свойства функции.
1. D (y) = R
х
2. E(y)= R
3. y(-x) = - y(x) нечётная
функция
4. Возрастает на R

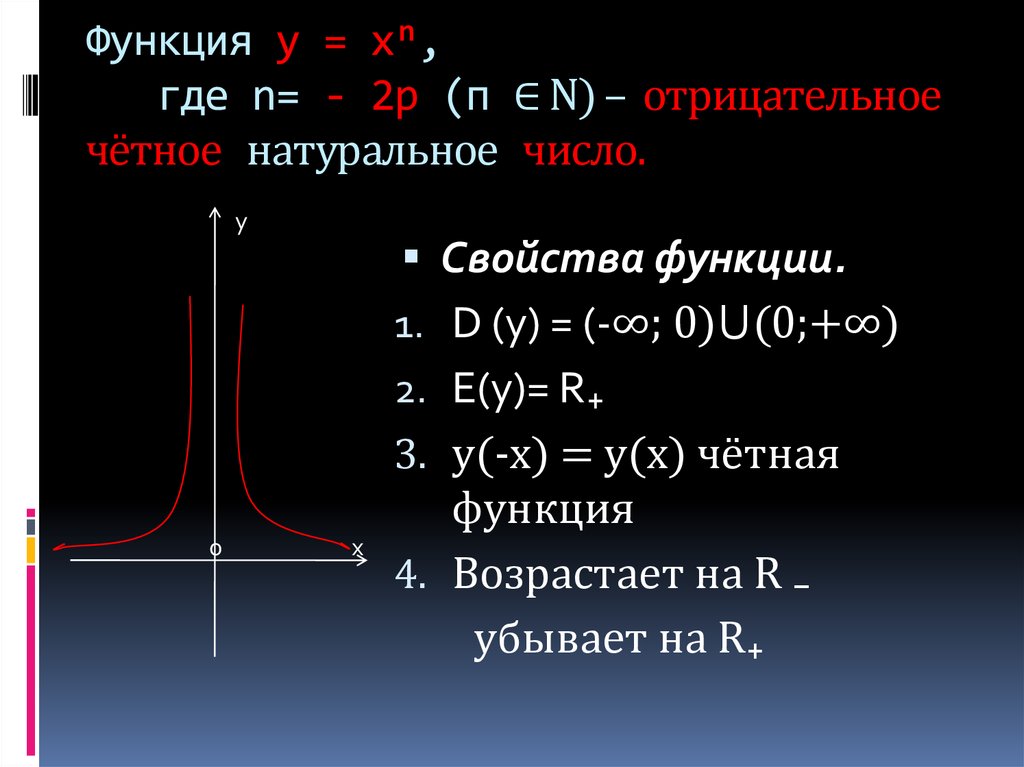
4. Функция у = хⁿ, где n= - 2р (п ∈ N) – отрицательное чётное натуральное число.

у
Свойства функции.
1. D (y) = (-∞; 0)⋃(0;+∞)
2. E(y)= R₊
3. y(-x) = y(x) чётная
0
х
функция
4. Возрастает на R ₋
убывает на R₊

5. Функция у = хⁿ, где n=-(2р + 1) (п ∈ N) – отрицательное нечётное натуральное число.

Функция у = хⁿ,
где n=-(2р + 1) (п ∈ N) –
отрицательное нечётное натуральное
число.у
Свойства функции.
1. D (y) = R, кроме х = 0
2. E(y)= R, кроме х = 0
0
х
3. y(-x) = - y(x) нечётная
функция
4. Убывает на R, кроме
х=0

6. Функция у = хⁿ, где n –положительное действительное дробное число.

у
<1
у = хⁿ, где п
0
х
Свойства функции.
1. D (y) = [0; +∞)
2. E(y)= [0; +∞)
y
3. Возрастает на [0;+∞)
y = xⁿ ,где п > 1
0
х

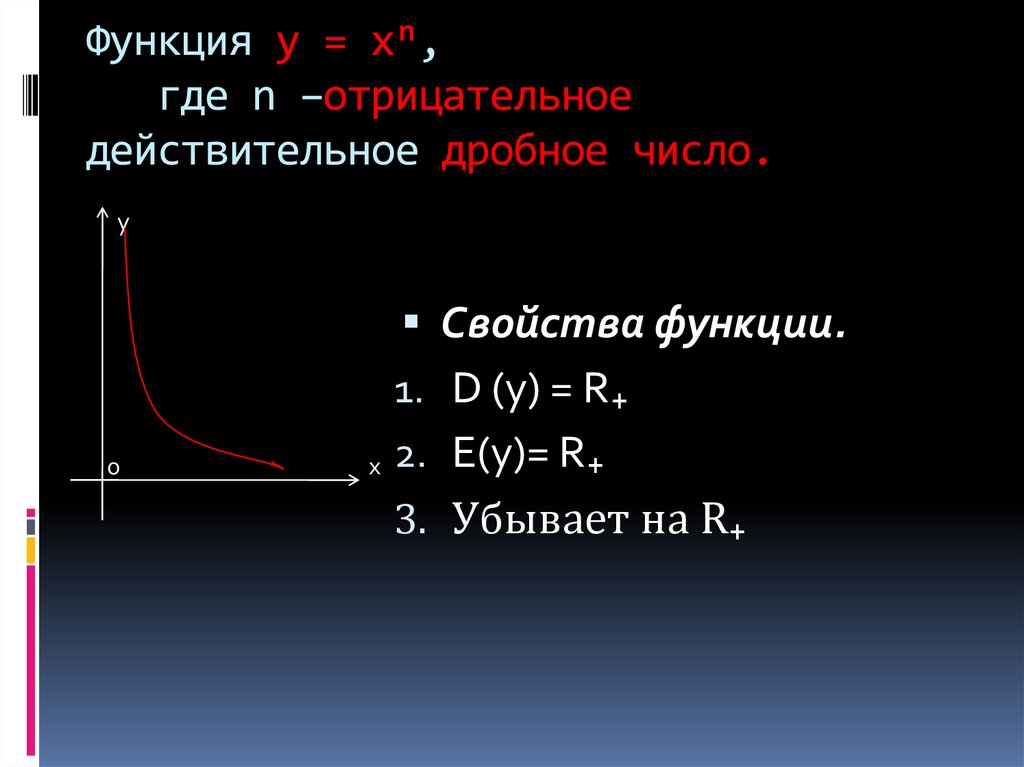
7. Функция у = хⁿ, где n –отрицательное действительное дробное число.

у
Свойства функции.
0
х
1. D (y) = R₊
2. E(y)= R₊
3. Убывает на R₊

8. ПРИМЕРЫ: Сравнить значения выражения.

а) 8,5²·¹ и 1
г) 3,1⁰·³ и 3,2 ⁰·³
б) 0,3¯⁰·² и 1
д) 0,3¯⁵·² и 0,2 ¯⁵·²
в) √7⁰·³ и 1
е) 2,5¯³ и 2,8¯³