Степенные функции, их свойства и графики

1. Степенные функции, их свойства и графики.

Алгебра, 10 класс
Математика, 1 курс
Автор: Тимошенко Л.Л.

2.

Опр.Степенной функцией называется функция вида y=xp
где p - заданное действительное число.
Рассмотрим различные случаи в зависимости от показателя
степени p, где n N - натуральное число:
1.
2.
3.
4.
5.
6.
Показатель p=2n – 1 - нечётное натуральное число.
Показатель 2n - чётное натуральное число.
Показатель p= –(2n–1) – целое, отрицательное, нечётное.
Показатель p= –2n – целое, отрицательное, чётное.
Показатель p>0, p R - положительное действительное нецелое число.
Показатель p<0, p R - отрицательное действительное нецелое число.

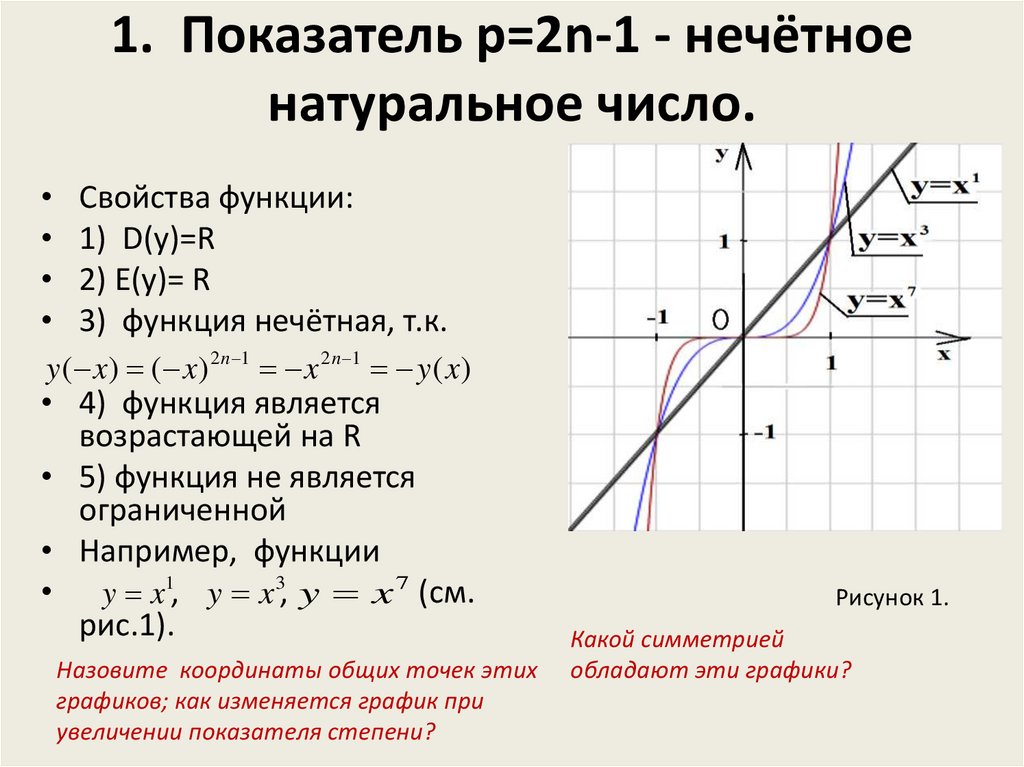
3. 1. Показатель p=2n-1 - нечётное натуральное число.

Свойства функции:
1) D(y)=R
2) E(y)= R
3) функция нечётная, т.к.
y ( x) ( x) 2 n 1 x 2 n 1 y ( x)
• 4) функция является
возрастающей на R
• 5) функция не является
ограниченной
• Например, функции
• y x1, y x 3, y x 7 (см.
рис.1).
Назовите координаты общих точек этих
графиков; как изменяется график при
увеличении показателя степени?
Рисунок 1.
Какой симметрией
обладают эти графики?

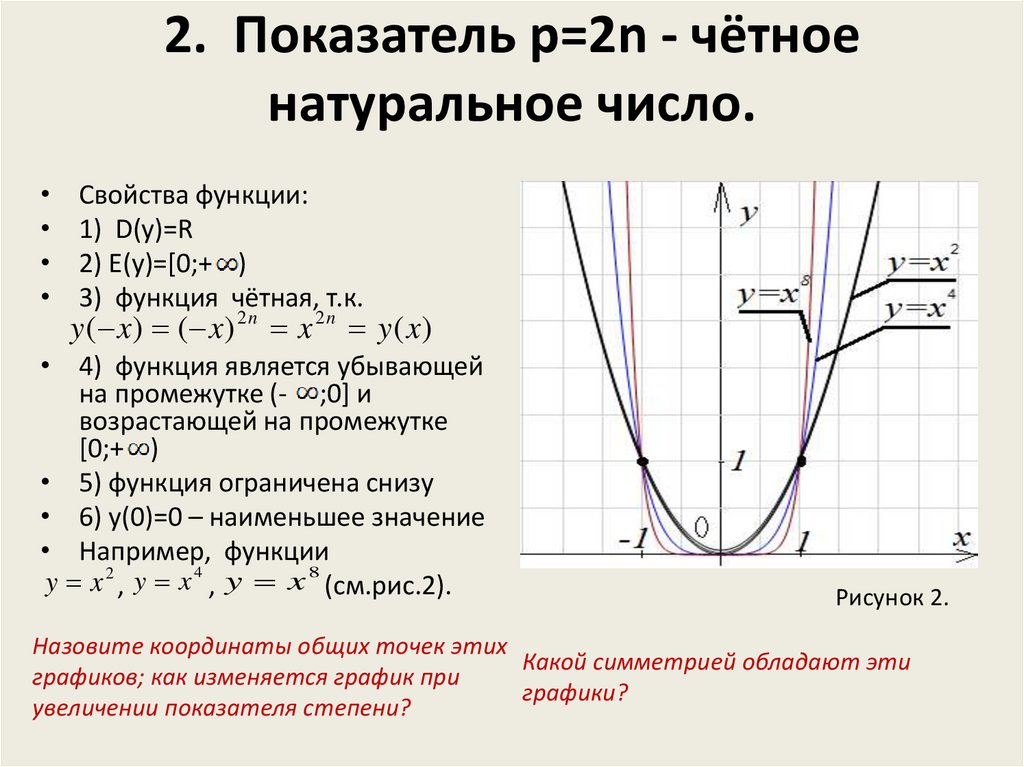
4. 2. Показатель p=2n - чётное натуральное число.

Свойства функции:
1) D(y)=R
2) E(y)=[0;+ )
3) функция чётная, т.к.
y ( x) ( x) 2 n x 2 n y ( x)
• 4) функция является убывающей
на промежутке (- ;0] и
возрастающей на промежутке
[0;+ )
• 5) функция ограничена снизу
• 6) у(0)=0 – наименьшее значение
• Например, функции
y x 2 , y x 4 , y x 8 (см.рис.2).
Рисунок 2.
Назовите координаты общих точек этих
Какой симметрией обладают эти
графиков; как изменяется график при
графики?
увеличении показателя степени?

5. 3. Показатель p= -(2n-1), где nϵN- натуральное число.

3. Показатель p= -(2n-1), где nϵNнатуральное число.
• Свойства функции:
• 1) D(y)=(- ;0)U(0;+ )
• 2) E(y)=(- ;0)U(0;+ )
• 3) функция нечётная, т.к.
y ( x) ( x) ( 2 n 1) 1 /( x) 2 n 1
1 /( x 2 n 1 ) x ( 2 n 1) y ( x)
• 4) функция является
убывающей
на промежутках (- ;0) и (0;+ )
• 5) функция не ограничена
• Например, функции
y x 1, y x 3 , y x 7 (см.рис.3).
Рисунок 3.
Назовите координаты общих точек этих
Какой симметрией обладают эти
графиков; как изменяется график при
графики?
увеличении модуля показателя степени?

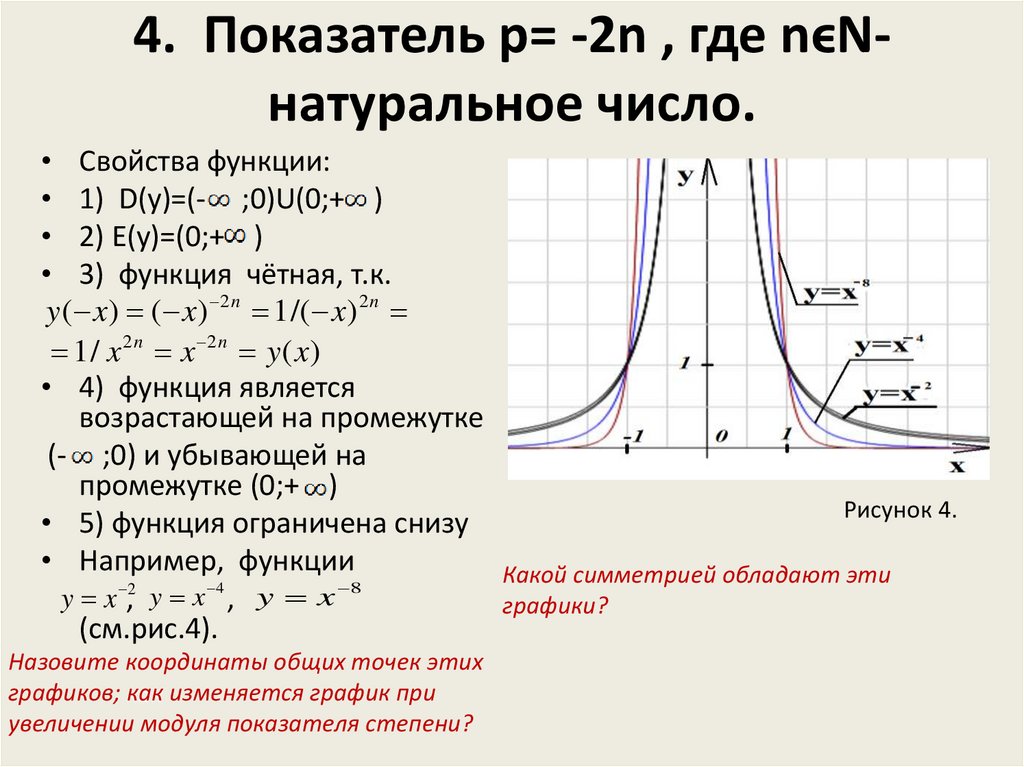
6. 4. Показатель p= -2n , где nϵN- натуральное число.

4. Показатель p= -2n , где nϵNнатуральное число.
• Свойства функции:
• 1) D(y)=(- ;0)U(0;+ )
• 2) E(y)=(0;+ )
• 3) функция чётная, т.к.
y ( x) ( x) 2 n 1 /( x) 2 n
1 / x 2 n x 2 n y ( x)
• 4) функция является
возрастающей на промежутке
(- ;0) и убывающей на
промежутке (0;+ )
Рисунок 4.
• 5) функция ограничена снизу
• Например, функции
Какой симметрией обладают эти
4
8
2
y x, y x , y x
графики?
(см.рис.4).
Назовите координаты общих точек этих
графиков; как изменяется график при
увеличении модуля показателя степени?

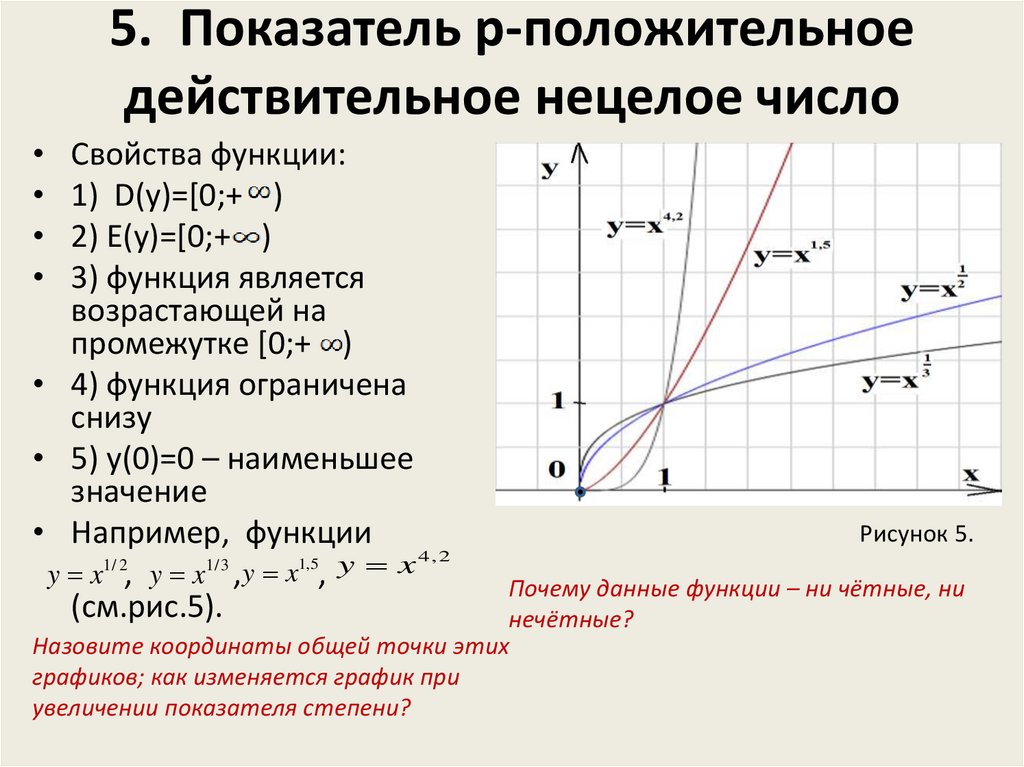
7. 5. Показатель p-положительное действительное нецелое число

Свойства функции:
1) D(y)=[0;+ )
2) E(y)=[0;+ )
3) функция является
возрастающей на
промежутке [0;+ )
• 4) функция ограничена
снизу
• 5) у(0)=0 – наименьшее
значение
• Например, функции
4, 2
1, 5 y x
1/ 2
1/ 3
y x , y x ,y x ,
(см.рис.5).
Рисунок 5.
Почему данные функции – ни чётные, ни
нечётные?
Назовите координаты общей точки этих
графиков; как изменяется график при
увеличении показателя степени?

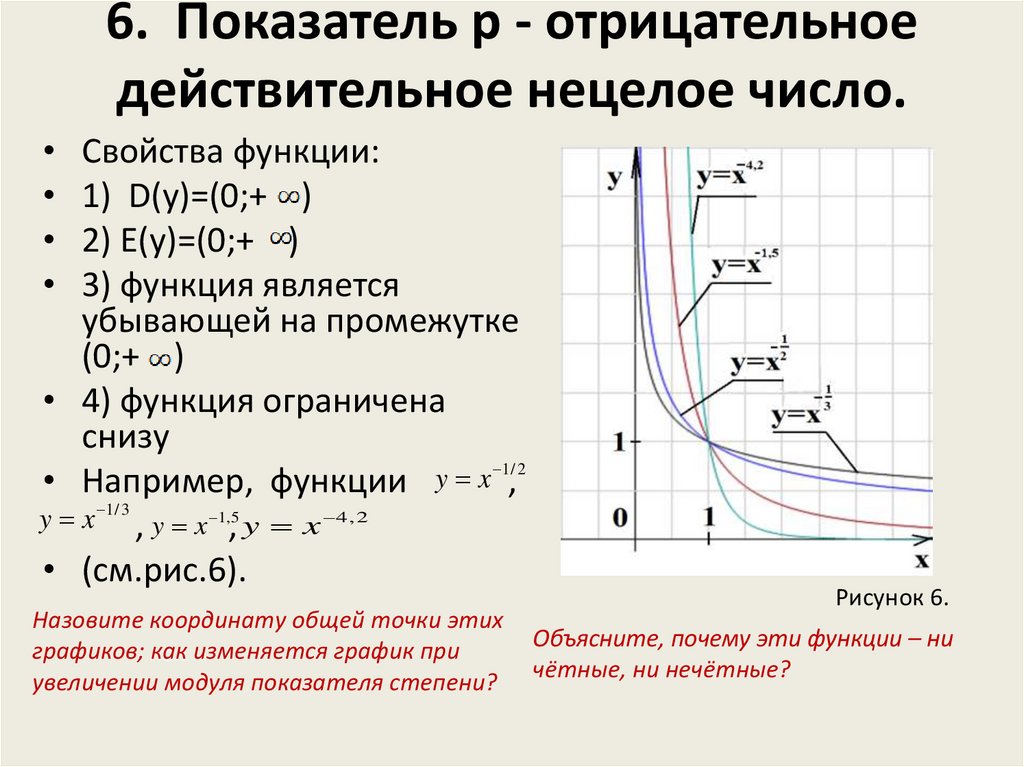
8. 6. Показатель p - отрицательное действительное нецелое число.

Свойства функции:
1) D(y)=(0;+ )
2) E(y)=(0;+ )
3) функция является
убывающей на промежутке
(0;+ )
• 4) функция ограничена
снизу
• Например, функции y x 1,/ 2
y x 1/ 3 , y x 1,,5 y x 4 , 2
• (см.рис.6).
Назовите координату общей точки этих
графиков; как изменяется график при
увеличении модуля показателя степени?
Рисунок 6.
Объясните, почему эти функции – ни
чётные, ни нечётные?

9.

Используемые источники:
1.Алгебра и начала анализа. 10-11 классы/ Ш.А.Алимов, Ю.М.Колягин
и др..-М.: Просвещение, 2011
2. Сайт www.yotx.ru