График и свойства степенной функции

1.

График и свойства
степенной функции
10 класс Алгебра и начала анализа
Ш.А. Алимов, Ю.М. Колягин и другие
Автор: учитель математики
ГБОУ средняя школа №368
г. С-Петербург
Бобель Юлия Анатольевна

2. Оглавление

Определение степенной функции
p = 2n, p = 2n-1, где n-натуральное число
p = -2n, p = -(2n-1), где n-натуральное число
p =m, где m>1, 0<m<1, m-нецелое число
p =m, где m<0, m-нецелое число

3.

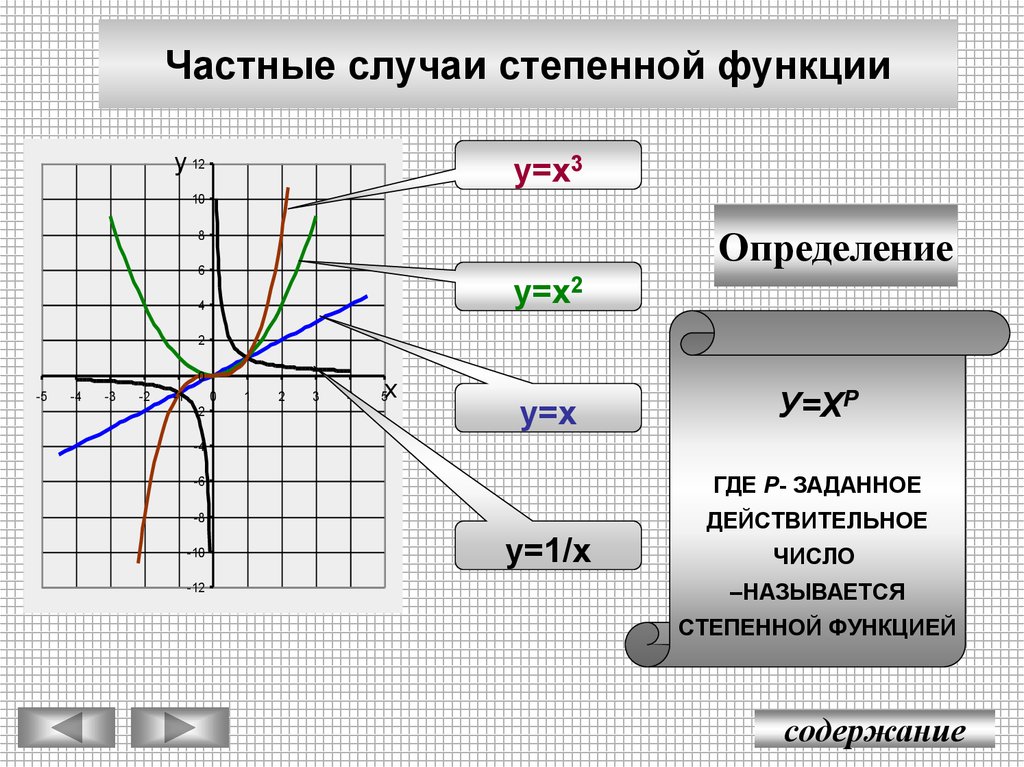
Частные случаи степенной функции
у 12
у=х3
10
Определение
8
6
у=х2
4
2
0
-5
-4
-3
-2
-1
-2
0
1
2
3
4
х
5
у=х
У=ХР
-4
-6
ГДЕ Р- ЗАДАННОЕ
-8
ДЕЙСТВИТЕЛЬНОЕ
-10
-12
у=1/х
ЧИСЛО
–НАЗЫВАЕТСЯ
СТЕПЕННОЙ ФУНКЦИЕЙ
содержание

4.

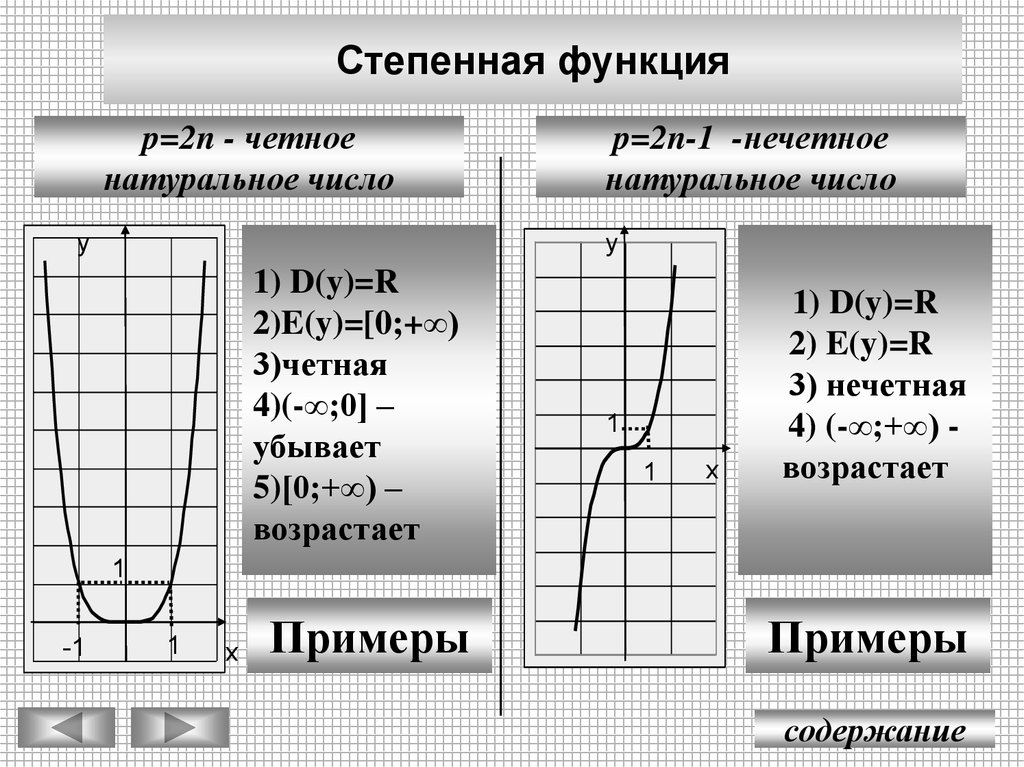
Степенная функция
p=2n - четное
натуральное число
у
p=2n-1 -нечетное
натуральное число
у
1) D(y)=R
2)E(y)=[0;+∞)
3)четная
4)(-∞;0] –
убывает
5)[0;+∞) –
возрастает
1
1
х
1) D(y)=R
2) E(y)=R
3) нечетная
4) (-∞;+∞) возрастает
1
-1
1
х
Примеры
Примеры
содержание

5. Примеры

p=2n – четное натуральное число
17
у
16
у=х2
15
14
13
12
у=х4
11
10
9
8
7
6
у=х6
5
4
3
2
1
-5
-4
-3
-2
0
-1 -1 0
1
2
3
4
5
х
содержание

6. Примеры

8
у
p=2n-1 -нечетное
натуральное число
7
6
5
4
у=х3
3
2
1
0
-3
-2
-1
-1 0
1
2
3х
у=х5
-2
-3
-4
-5
у=х7
-6
-7
-8
содержание

7.

Степенная функция
p= -2n
n - натуральное число
у
у
1) D(y)=R, x≠0
2)E(y)=(0;+∞)
3)четная
4)(-∞;0) –
возрастает
5)(0;+∞) –
убывает
1
-1
p= -(2n-1)
n - натуральное число
1
х
Примеры
1
-1 -1 1
х
1) D(y)=R, х≠0
2) E(y)=(-∞;0)
(0; +∞)
3) нечетная
4) (-∞;0);(0;+∞) –
убывает
Примеры
содержание

8.

Примеры
p= -2n, n - натуральное число
у
7
у=х-2
6
5
4
у=х-4
3
2
у=х-6
1
0
-4
-3
-2
-1
0
1
2
3
4
х
содержание

9.

Примеры
p= -(2n-1) , n - натуральное число
9
у
8
7
6
у=х-1
5
4
3
у=х-3
2
1
0
-5
-4
-3
-2
-1 -1 0
-2
-3
1
2
3
4
5
х
у=х-5
-4
-5
-6
-7
-8
-9
содержание

10.

Степенная функция
p= m, m>1,
m-нецелое число
p= m , 0<m<1
m - нецелое число
у
у
1) D(y)=[0;+∞)
2)E(y)=[0;+∞)
3) [0;+∞) –
возрастает
1
1
х
1)D(y)=[0;+∞)
2) E(y)=[0;+∞)
3) [0;+∞) - возрастает
1
0 1
х
Примеры
Примеры
содержание

11.

Примеры
p= m, m>1, m-нецелое число
9
у
8
у=х2,7
7
6
5
у=х1,5
4
3
у=х1,3
2
1
0
0
1
2
3
4
5
х
содержание

12.

Примеры
p= m , 0<m<1, m - нецелое число
у
4
у=х0,7
3
2
у=х0,5
1
0
0
1
2
3
4
5
х
у=х0,3
содержание

13.

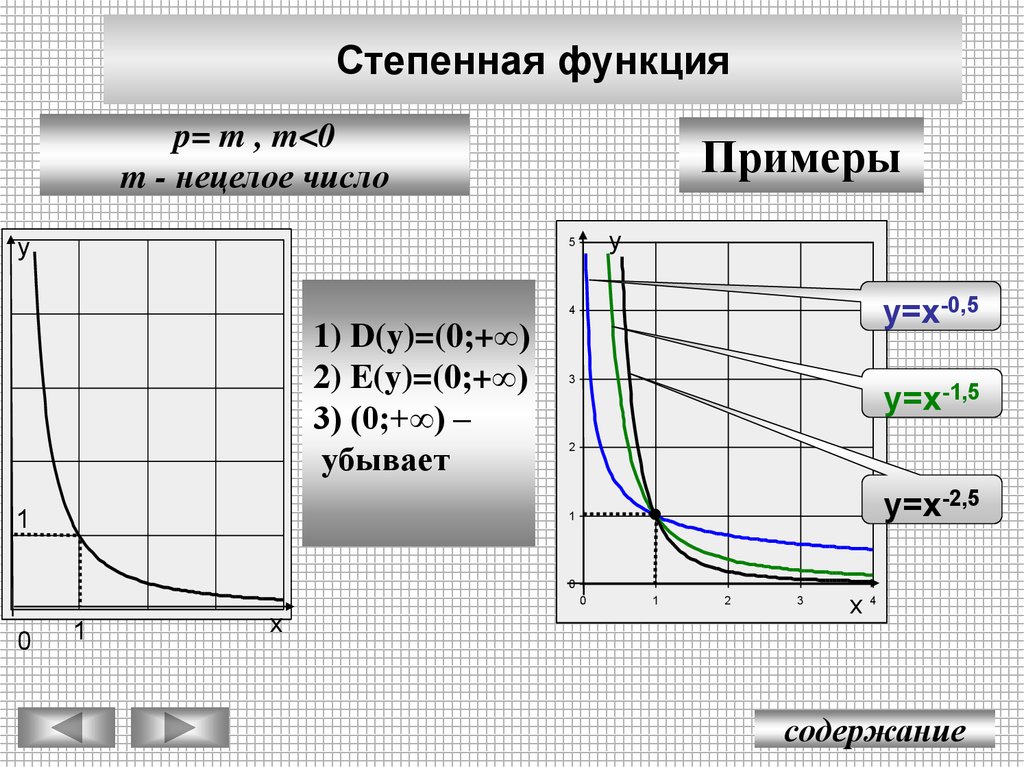
Степенная функция
p= m , m<0
m - нецелое число
у
Примеры
у
5
у=х-0,5
4
1) D(y)=(0;+∞)
2) E(y)=(0;+∞)
3) (0;+∞) –
убывает
3
у=х-1,5
2
у=х-2,5
1
1
0
0
0
1
х
1
2
3
х4
содержание

14.

Степенная функция
№123(2)
№124(1)
у
3
у
3
у х
2
4
3
2
у=х
у=х
1
1
1
0
0
11
4
3
2
х х
при х>1
х х
при 0<х<1
4
3
х3
у х
0
1
0
1
1
х 1 х
х х
2
3
х4
при 0<х<1
при х>1
содержание

15.

Степенная функция
Устные упражнения.
Найти область определения функции:
1) у 5 х 3
1) x є R
2)
3
у
х 1
2) x≠1
3)
у х 2
3) x≥2
4)
у
1
х 2
5) у = 2 х2 – 5 х+1.
4) x>2
5) x є R
содержание

16.

Степенная функция
Устные упражнения.
Сравните значения выражений:
1) 2 ,7 2 ,7 и 2,9 2,7
1)
2 ,7 2 ,7 2,9 2,7
2) 0 ,5 0 ,5 и 0,20,5
2)
0 ,5 0 ,5 0,2 0,5
3)
2 ,5 2 ,5 1
3)
2 ,5 2 ,5 и 1
4) ( 2 6 ) 0 ,2 и ( 6 2 ) 0 ,2
4) ( 2 6 ) 0 ,2 ( 6 2 ) 0 ,2
5) 5 ,3 и 2,3-
5)
6)
3
4
14 15
и
15 16
3
4
5 ,3 2,3 -
3
4
6)
14 15
15 16
3
4
содержание

17.

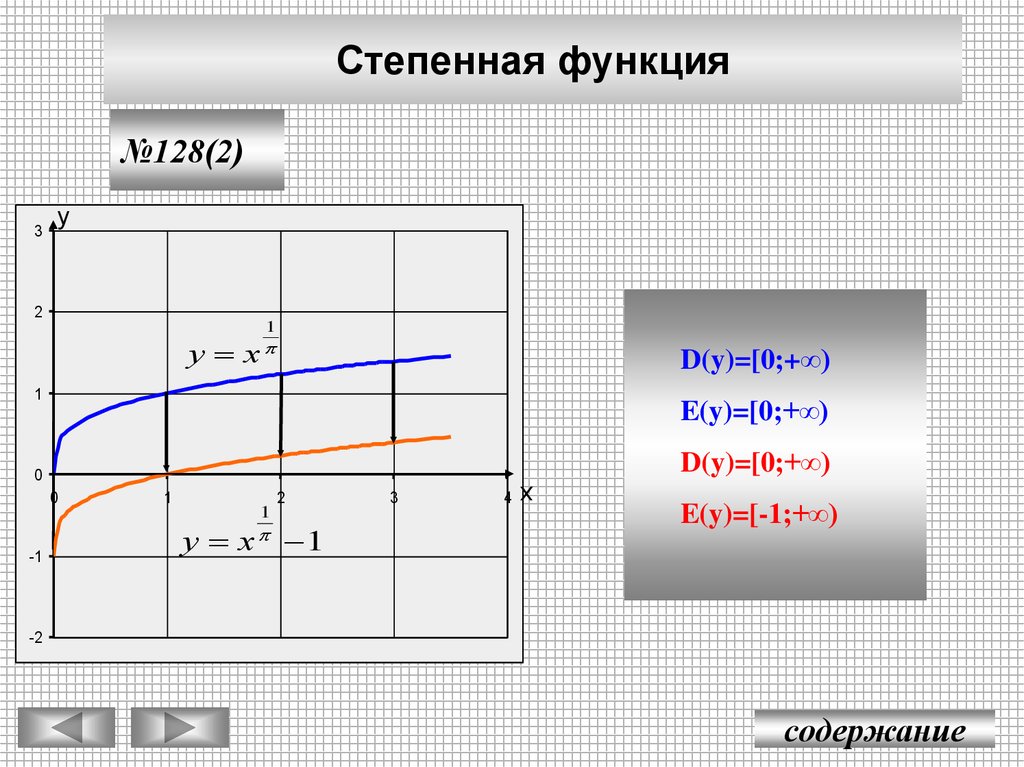
Степенная функция
№128(2)
3
у
2
1
у х
D(y)=[0;+∞)
1
E(y)=[0;+∞)
0
0
-1
1
1
2
у х 1
3
4
х
D(y)=[0;+∞)
E(y)=[-1;+∞)
-2
содержание

18.

Степенная функция
№128(3)
3
у
у х
2
D(y)=[0;+∞)
у ( х 2)
E(y)=[0;+∞)
D(y)=[2;+∞)
1
E(y)=[0;+∞)
0
0
1
2
3
4
х
содержание

19.

Степенная функция
Построить график функции:
у ( х 2 ) 2 3
4
3
2
1
0
-4
-3
-2
-1
0
-1
1
2
3
4
1)D(y)=(-∞;-2)
y = х-2 (-2;+∞)
2)E(y)=(-3;+∞)
3) (-∞;-2) –
возрастает
4) (-2;+∞)
– -2
у=(х+2)
убывает
-2
-3
у=(х+2)-2 - 3
-4
содержание

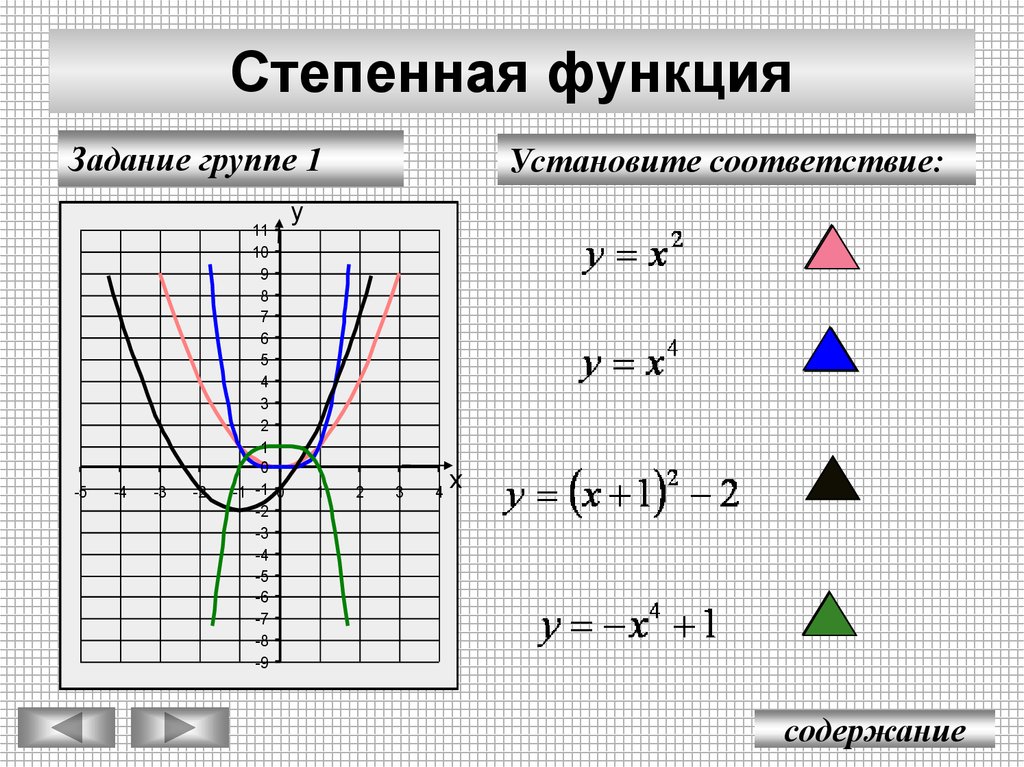
20. Степенная функция

Задание группе 1
-5
-4
-3
-2
11
10
9
8
7
6
5
4
3
2
1
0
-1 -1 0
-2
-3
-4
-5
-6
-7
-8
-9
Установите соответствие:
у
1
2
3
4
х
содержание

21. Степенная функция

Задание группе 2
Установите соответствие:
уу
5
4
3
2
1
0
-5
-4
-3
-2
-1
-1
0
1
2
3
4
х
5
-2
-3
-4
-5
содержание

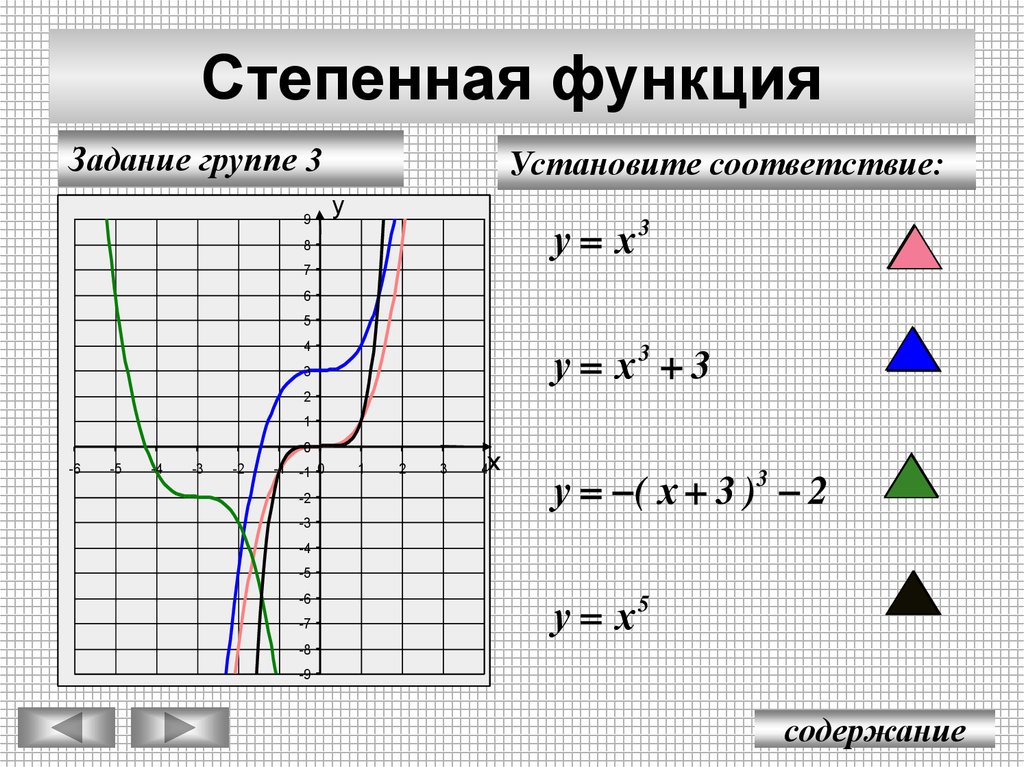
22. Степенная функция

Задание группе 3
9
Установите соответствие:
у
у х3
8
7
6
5
4
у х3 3
3
2
1
0
-6
-5
-4
-3
-2
-1 -1 0
-2
1
2
3
х
4
у ( х 3 )3 2
-3
-4
-5
-6
-7
у х5
-8
-9
содержание

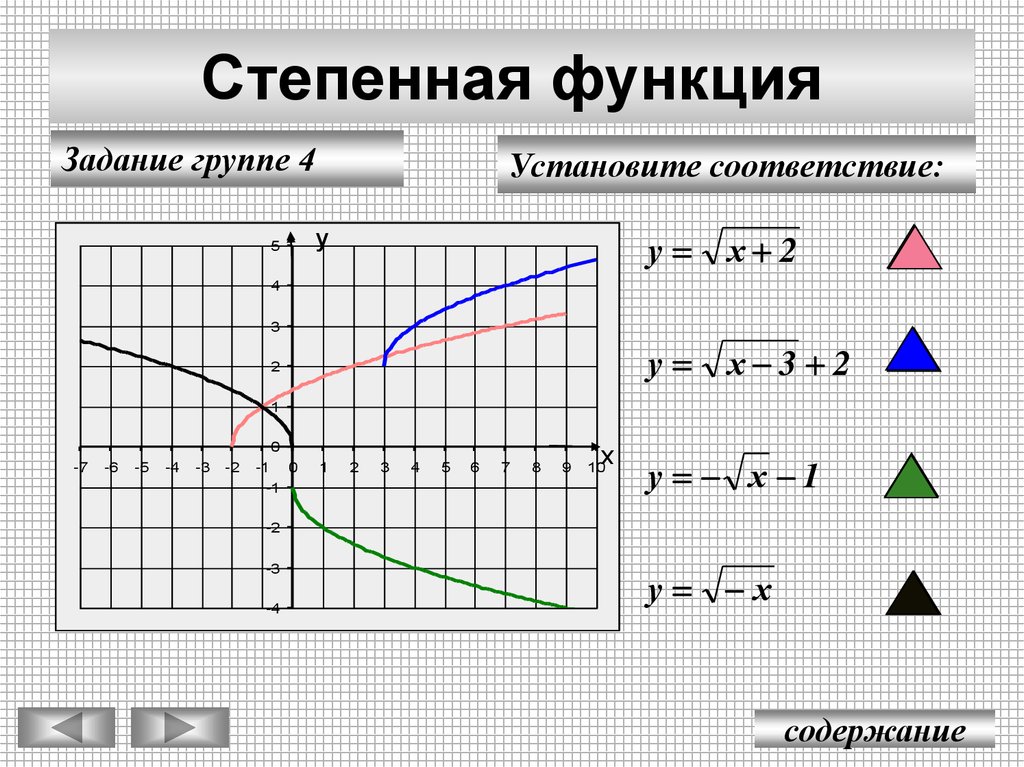
23. Степенная функция

Задание
Задание группе
группе 44
5
Установите соответствие:
у
у
х 2
у
х 3 2
4
3
2
1
0
-7
-6
-5
-4
-3
-2
-1 0
-1
1
2
3
4
5
6
7
8
9
х
10
у х 1
-2
-3
-4
у х
содержание

24. Степенная функция

Открытый банк ЕГЭ 2012 В12 №28193
Для определения эффективной температуры звeзд используют закон Стефана–
Больцмана, согласно которому мощность излучения нагретого тела P,
измеряемая в ваттах, прямо пропорциональна площади его поверхности и
четвeртой степени температуры:
, где
— постоянная,
площадь S измеряется в квадратных метрах, а температура T — в градусах
Кельвина. Известно, что некоторая звезда имеет площадь
излучаемая ею мощность P не менее
м2 , а
Вт. Определите наименьшую
возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
содержание

25. Степенная функция

Открытый банк ЕГЭ 2012 В12 №28195
Для определения эффективной температуры звeзд используют
закон Стефана–Больцмана, согласно которому мощность
излучения нагретого тела P, измеряемая в ваттах, прямо
пропорциональна площади его поверхности и четвeртой
степени температуры:
, где
— постоянная,
площадь S измеряется в квадратных метрах, а температура
T — в градусах Кельвина. Известно, что некоторая звезда имеет
площадь
менее
м2 , а излучаемая ею мощность P не
Вт. Определите наименьшую возможную
температуру этой звезды. Приведите ответ в градусах Кельвина.
содержание

26. Список литературы

1.
Ш.А. Алимов «Алгебра и начала анализа 10-11» М.,
Просвещение, 2005.
2. Н.Е. Федорова «Изучение алгебры и начал анализа в
10-11 классах», М., Просвещение, 2004.
3.
Наглядный справочник по алгебре, Москва-Харьков,
Илекса, 1997 г.
4. Открытый банк ЕГЭ 2012
http://mathege.ru/or/ege/ShowProblems.html?posMask=2048