урок 8 Функции

1. Урок №8. Степенная функция, её свойства и график

Минакова Дарья Владимировна

2. Определение

› Функция вида у = хn где n – любое действительное
число, называется степенной функцией

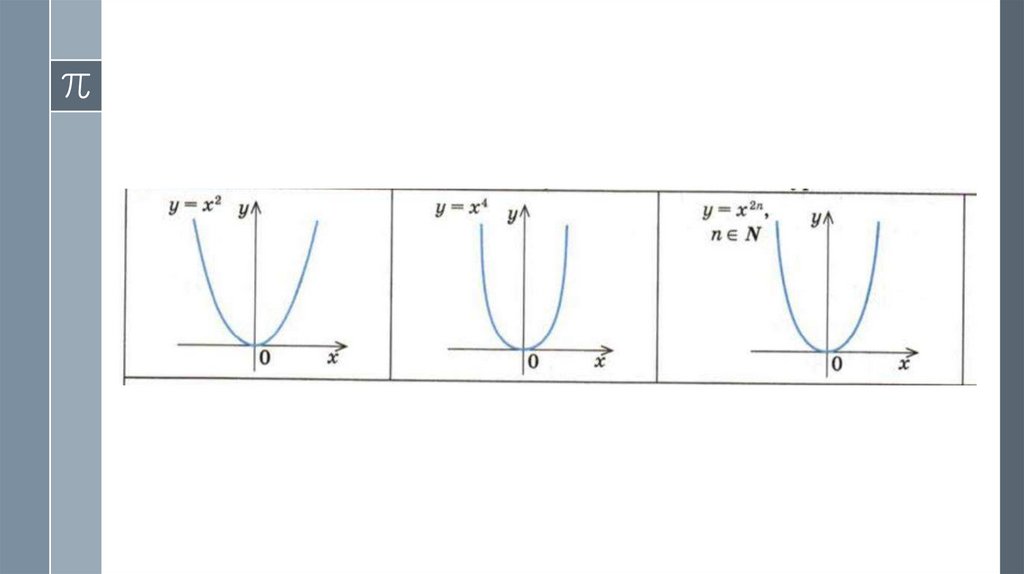
3. 1. Функция вида у = ха (а — четное натуральное число).

› Область определения функции у = х2n: D(y) = R
› Функция четная: если f (х) = х2n, то f (-x) = (-х)2n = х2n = f
(х). Таким образом, график функции у = х2n
симметричен относительно оси Оу.
› Поскольку при х = 0 значение у = 0, то график функции
у = х2n всегда проходит через начало координат.
› На промежутке [0; +∞) функция возрастает.

4.

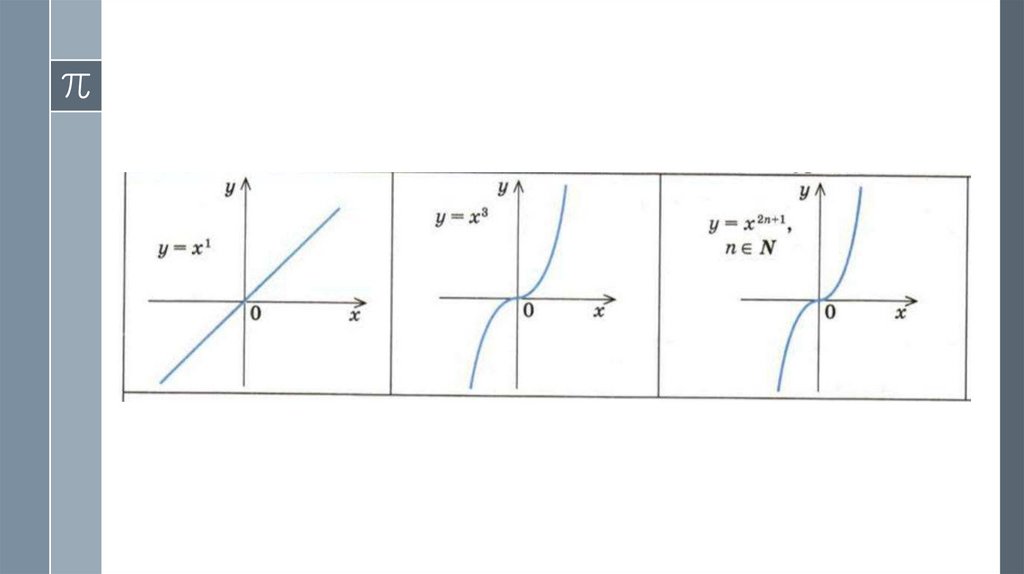
5. 2. Функция у = ха (а — нечетное натуральное число).

› Область определения функции у = х2n+1: D (y) = R
› Функция нечетная: если f (х) = х2n+1, то f (-х) = (-х)2n+1 = х2n+1 = -f (x).
› Таким образом, график функции симметричен
относительно начала координат.
› Поскольку при х = 0 значение у = 0, то график функции
у = х2n+1 всегда проходит через начало координат.
› На всей области определения функция возрастает.

6.

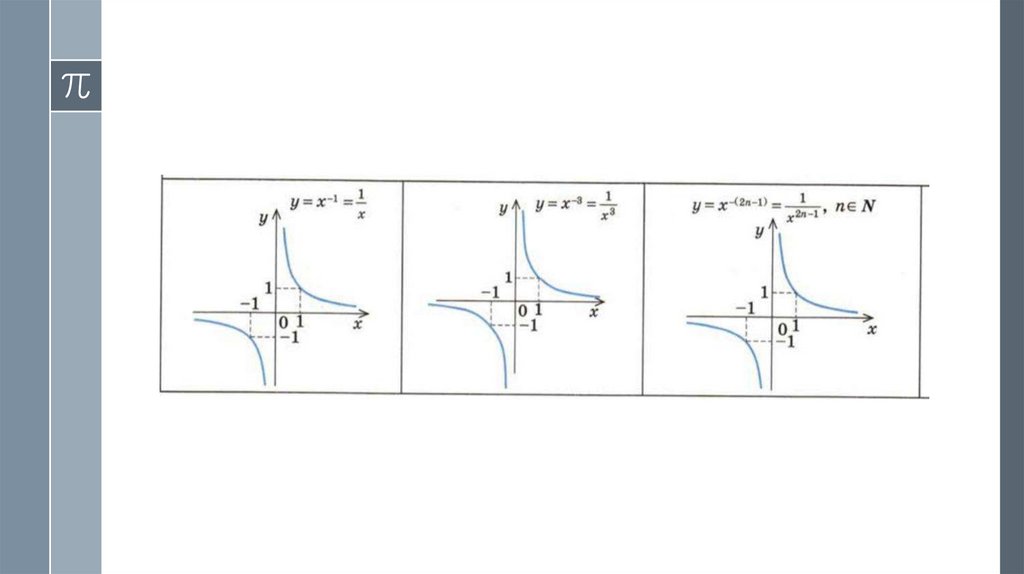
7. 3. Функция у = ха (а — нечетное отрицательное число).

› Область определения функции у = х-(2n-1) =
, то есть D (y) = (-∞; O)U(0; +∞), поскольку значение этой
функции можно вычислить при любых значениях х, кроме х =
0.
› Функция нечетная: при х ≠ 0, если f (x) = х-2n то
› f (-x) = (-x) -(2n-1) = - х -(2n-1) = - f (x).
› Таким образом, график функции симметричен относительно
начала координат.
› Учитывая, что х ≠ 0 и у ≠ 0 у = х -(2n-1) = ≠ 0 получаем, что
график функции у = х -(2n-1) не пересекает оси координат

8.

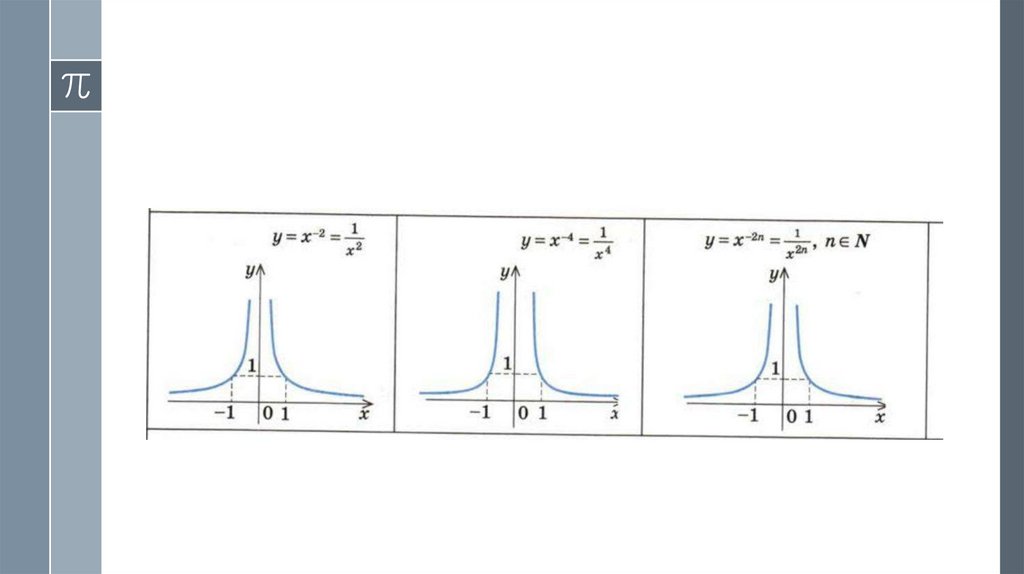
9. 4. Функция у = ха (а — четное отрицательное число).

› Область определения функции y = x-2n =
, то есть
D (y) = (- ∞; 0) U (0; + ∞), поскольку значение этой
функции можно вычислить при любых значениях х,
кроме х = 0.
› Функция четная: при х ≠ 0, если f (х) = x-2n , то
f (-х) = (-x) -2n = x-2n = f (х). Таким образом, график
функции симметричен относительно оси Оу.
› Учитывая, что при х ≠ 0 значение у = x-2n = >0,
получаем, что график функции у = x-2n не пересекает
оси координат.

10.

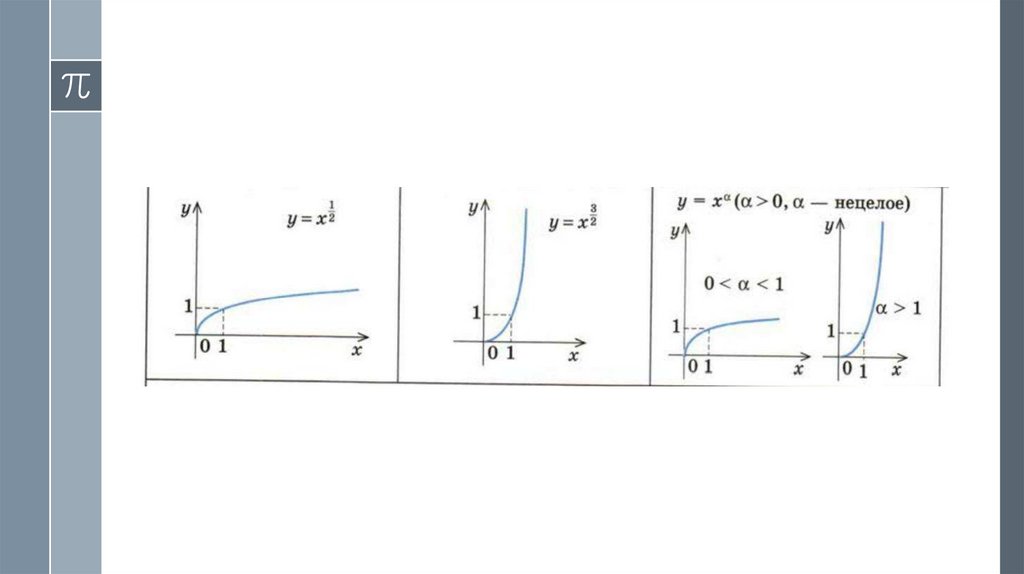
11. 5. Функция у = ха (а - нецелое положительное число).

› Область определения: х > 0, то есть D (y) = [0; +∞),
поскольку значение степени с положительным не целым
показателем определено только для не отрицательных
значений х .
› Тогда область определения несимметрична относительно
точки 0, и функция не может быть ни четной, ни нечетной.
› Поскольку при х = 0 значение у = 0, то график функции у =
ха (а > 0) всегда проходит через начало координат.
› При х > 0 значение у = ха > 0.
› Можно обосновать, что на всей области определения
функция у = ха (а > 0) является возрастающей.

12.

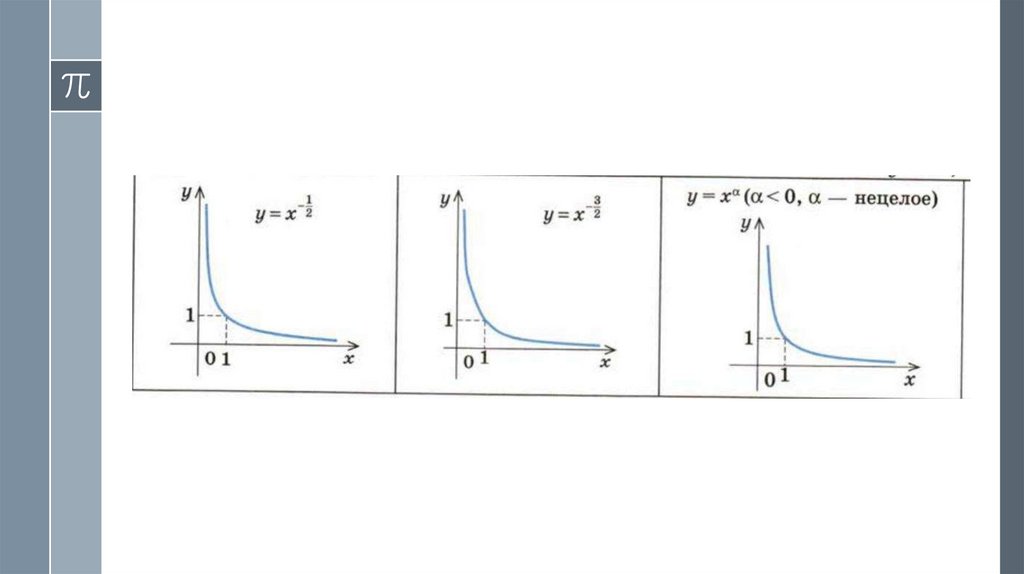
13. 6. Функция у = ха ( а — нецелое отрицательное число ).

› Область определения: х > 0 D = (0; +∞), поскольку
значение степени с отрицательным нецелым
показателем определено только для положительных
значений х.
› Функция несимметрична относительно точки 0, и не
может быть ни четной, ни нечетной.
› Учитывая, что при х > 0 значения у = ха > 0 (то есть х ≠
0 и у ≠ 0), получаем, что график функции у = ха (а < 0)
не пересекает оси координат.
› На промежутке (0; +∞) функция убывает