Степенная функция, её свойства и график

1.

Ст епенная функция, её свойст ва и график.
Холодные числа, внешне сухие формулы
математики полны внутренней красоты
и жара сконцентрированной в них мысли.
А. Д. Александров

2.

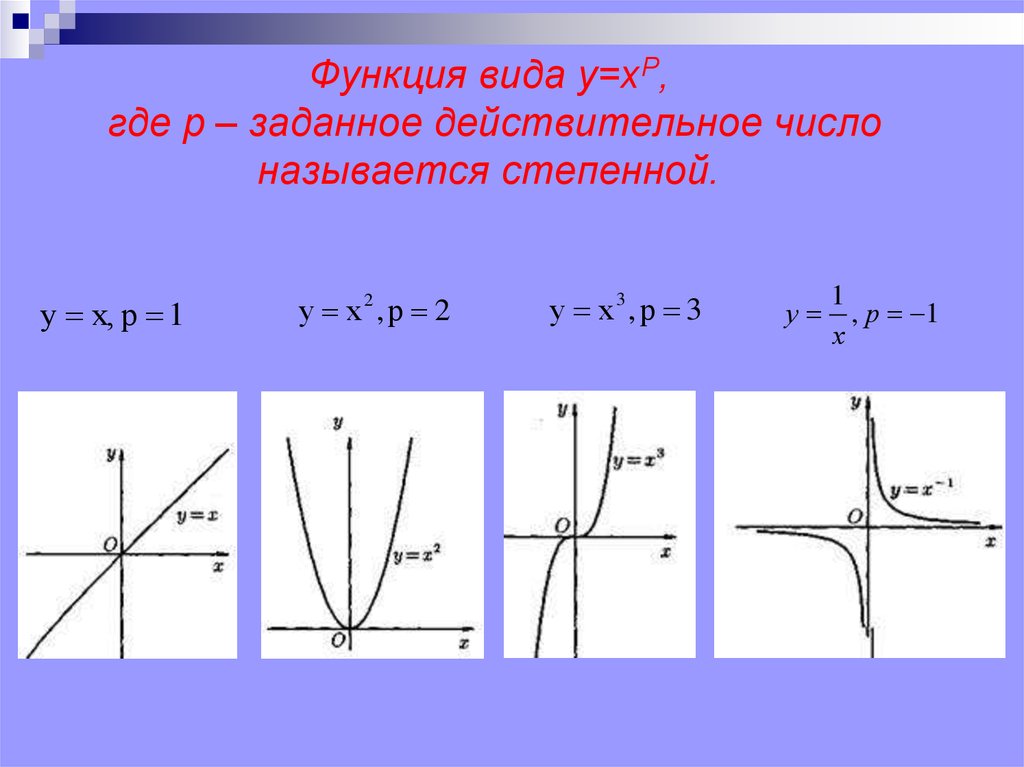
Устно:

3. Функция вида у=хР, где р – заданное действительное число называется степенной.

у х, р 1
у х2, р 2
у х3, р 3
у
1
, р 1
х

4.

Определение
Функция у f (x) , определенная на множестве Х,
называется ограниченной снизу на множестве Х,
если существует число С1, такое, что
для любого х Х выполняется неравенство f ( x) C1

5.

Определение
Функция у f (x) , определенная на множестве Х,
называется ограниченной сверху на множестве Х,
если существует число С2, такое, что
для любого х Х выполняется неравенство f ( x) C2

6.

Например:
1)функция у х 2 2 х является ограниченной снизу ,
т. к. х 2 2 х х 1 1 1;
2
2)функция у х 2 2 х 3 ограничена сверху,
т. к. х 2 2 х 3 4 ( х 1) 2 4
Функцию, ограниченную и сверху и снизу, на множестве Х,
называют ограниченной на этом множестве.

7.

Функция у f ( х) является ограниченной
на множестве Х тогда и только тогда,
когда существует число С 0, такое,
что для любого х Х выполняется неравенство
f ( х) С.
Функция у f ( х), х Х называется неограниченной ,
если для любого С 0 найдется значение хс Х ,
такое, что f ( хс ) C.

8.

Если существует такое значение х0 из области определения Х функции у f ( х),
что для любого х из этой области справедливо неравенство f ( x) f ( x0 ), то говорят ,
что функция у f ( х) принимает наименьшее значение у0 f ( х0 ) при х х0 .
Если существует такое значение х0 из области определения Х функции у f ( х),
что для любого х из этой области справедливо неравенство f ( x) f ( x0 ), то говорят ,
что функция у f ( х) принимает наибольшее значение у0 f ( х0 ) при х х0 .

9.

Свойства степенной функции при различных значениях р.
1.Показатель р 2n четное натуральное число.
у х 2 n , где n натуральное число.
Свойства :
1)Область определения все действительные числа,
т. е. множество R;
2) Множество значений все неотрицательные числа,
т. е. у 0;
3)Функция у х 2 n четная, т. к. ( х) 2 n х 2 n ;
4)Функция является убывающей на промежутке х 0
и возрастающей на промежутке х 0;
5)Функция ограничена снизу (так как х 2 n 0
для любого х R;
6)Функция принимает наименьшее значение у 0 при х 0,
так как f ( x) x 2 n 0 при x R и f (0) 0.

10.

Свойства степенной функции при различных значениях р.
2.Показатель р 2n 1 нечетное натуральное число.
у х 2 n 1 , где n натуральное число.
Свойства :
1)Область определения все действительные числа,
т. е. множество R;
2) Множество значений множество R;
3)Функция у х 2 n 1 нечетная, т. к. ( х) 2 n 1 х 2 n 1 ;
4)Функция является возрастающей на всей
действительной оси;
5)Функция не является ограниченной ни сверху ни снизу ;
6)Функция не принимает ни наименьшег о, ни наибольшего значений.

11.

Свойства степенной функции при различных значениях р.
3.Показатель р 2n, где n натуральное число.
у х 2 n , где n натуральное число.
Свойства :
1)Область определения множество R, кроме х 0;
2) Множество значений множество
положительных чисел у 0;
3)Функция у х 2 n
1
1
1
четная
,
т
.
к
.
;
2n
2n
2n
x
( x)
x
4)Функция является возрастающей на промежутке х 0
и убывающей на промежутке х 0;
5)Функция ограничена снизу : у 0;
6)Функция не принимает ни наименьшего,
ни наибольшего значений.

12.

Свойства степенной функции при различных значениях р.
4.Показатель р (2n 1), где n натуральное число.
у х ( 2 n 1) , где n натуральное число.
Свойства :
1)Область определения множество R, кроме х 0;
2) Множество значений множество R, кроме у 0;
3)Функция у х ( 2 n 1)
т. к.
1
x
2 n 1
нечетная,
1
1
;
( x) 2 n 1
x 2 n 1
4)Функция является убывающей
на промежутках х 0 и х 0;
5)Функция не является ограниченной;
6)Функция не принимает ни наименьшего,
ни наибольшего значений.

13.

Свойства степенной функции при различных значениях р.
5. Показатель р положительное действительное
нецелое число. у х р
Свойства :
1)Область определения множество
неотрицательных чисел, х 0;
2) Множество значений множество
неотрицательных чисел, у 0;
3)Функция не является ни четной,
ни нечетной;
4)Функция является возрастающей
на промежутке х 0;
5)Функция ограничена снизу : у 0;
6)Функция принимает наименьшее,
значение у 0 при х 0.

14.

Свойства степенной функции при различных значениях р.
6. Показатель р отрицательное действительное
нецелое число. у х р
Свойства :
1)Область определения множество
положительных чисел, х 0;
2) Множество значений множество
положительных чисел, у 0;
3)Функция не является ни четной,
ни нечетной;
4)Функция является , убывающей
на промежутке х 0;
5)Функция ограничена снизу : у 0;
6)Функция не принимает ни наименьшег о,
ни наибольшего значений.

15. Домашнее задание

§ 1 Стр. 166 – 172
№ 1 (2; 4)
2 (2)
3 (2)

16.

Свойства степенной функции у = хр
при различных значениях р.
Показатель р –
– четное натуральное число
– нечетное натуральное число
– четное отрицательное число
– нечетное отрицательное число
– положительное действительное нецелое число
– отрицательное действительное нецелое число

17. Домашнее задание

§ 1 Стр. 166 – 174
№ 5 (2; 4; 6)
4 (2; 4)
6 (2; 4)
8 (2)